Глава 12. Дифференциальные уравнения

Дата: 2025-04-30; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

12.1. Понятие комплексного числа

Комплексные числа – выражения вида 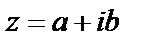, 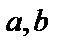– действительные числа, i – мнимая единица, 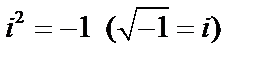. Числа действительные, 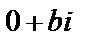– чисто мнимые.

Число a – действительная часть числа z , 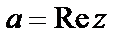, b – мнимая часть числа z , 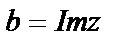, модуль: .

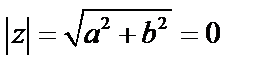Сопряжённое число 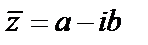(отличается знаком мнимой части). Два комплексных числа 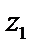и 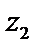равны, если 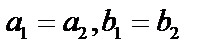.Комплексное число равно 0, если 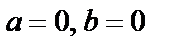. С комплексными числами можно производить арифметические операции (по правилам алгебры):

.

.

.

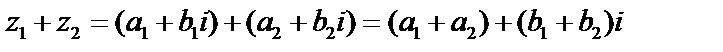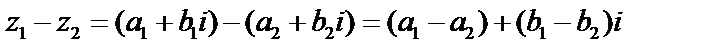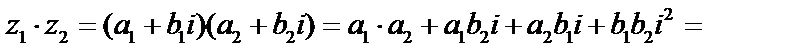
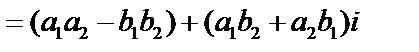
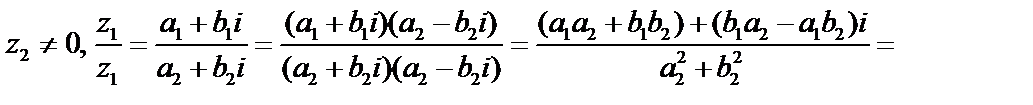
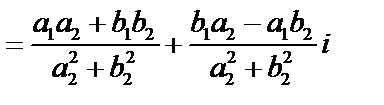Решение квадратного уравнения: .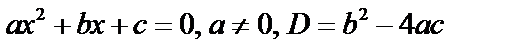

1) если 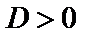, то 2 действительных корня: ,

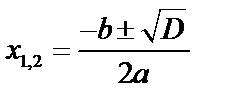2) если 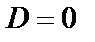, то ,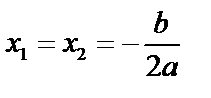

3) если 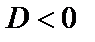, то 2 комплексных корня: .

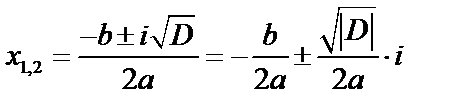Пример: Решить уравнение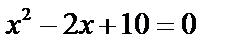

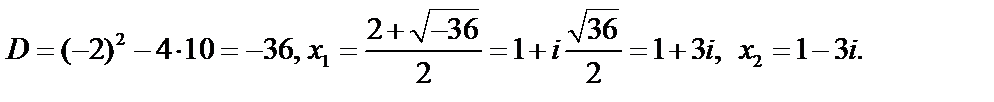
12.1. Тригонометрическая форма комплексного числа. Действия над комплексными числами в тригонометрической форме

Наряду с представлением комплексного числа в алгебраической форме: 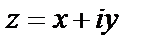, во многих случаях удобно пользоваться комплексным числом в полярных координатах.

Совмещая полюс полярной системы координат с началом декартовой системы координат,

а полярную ось с осью ОХ, точка 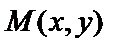будет иметь полярные координаты 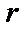и 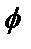, 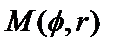. Декартовые координаты х и у точки 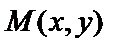связаны с её полярными координатам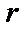и и 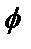соотношениями 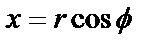, 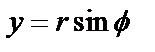и число 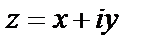запишется в форме: .

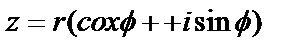Правую часть этого равенства называют тригонометрической формой комплексного числа z, угол 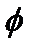– аргументом числа z и обозначают Arg z, r – модулем комплексного числа z и обозначают |z|. Модуль и аргумент комплексного числа z 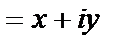находят по формулам:

, .

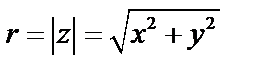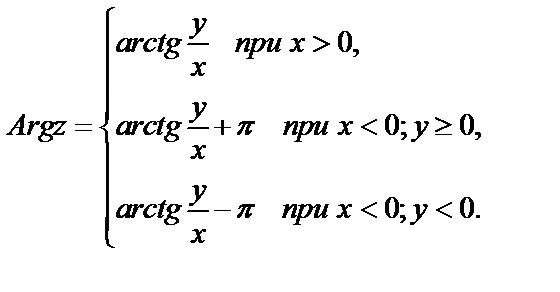
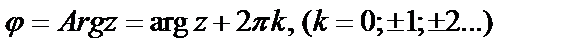Значение аргумента 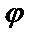, заключенное в границах, 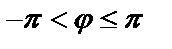называется главным значением аргумента и обозначается 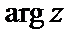. Для сопряженных комплексных чисел z и 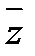модули равны, а главное значения их аргументов отличаются только знаком: .

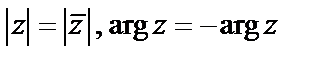Пример 1. Представить в тригонометрической форме следующее число: .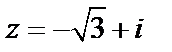

Решение. Модуль комплексного числа 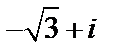определяется по формуле 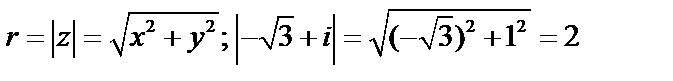. Так как число 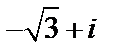лежит во второй четверти, по формуле найдем: 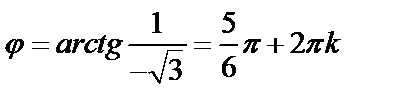. Подставляя значение модуля и аргумента в формулу, получаем .

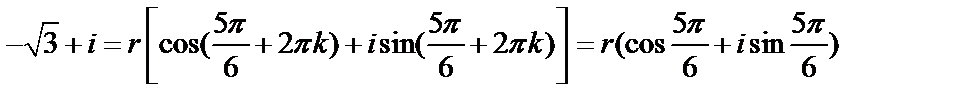Пример 2. Представить в тригонометрической форме следующее число: .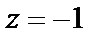

Решение. 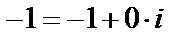Модуль числа 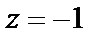будет равен 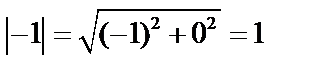а аргумент 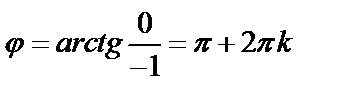. По найденным значениям модуля и аргумента число 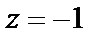в тригонометрической форме запишется так: .

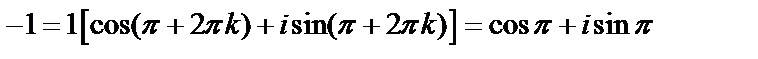Пример 3. Представить в тригонометрической форме следующее число: .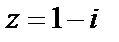

Решение. Согласно формулам, найдем: 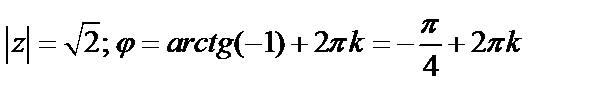. Так как число находится в четвертой четверти, получаем .

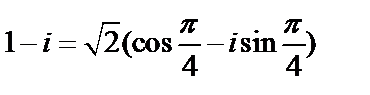Умножение и возведение в степень.

Пусть даны два комплексных числа в тригонометрической форме 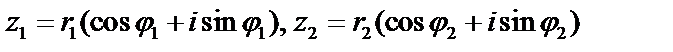, тогда ,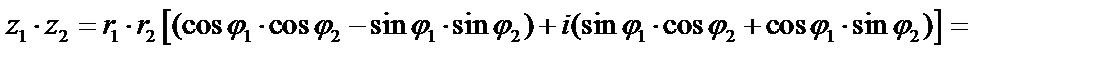

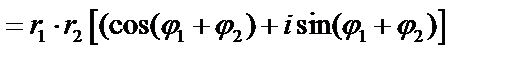т.е. 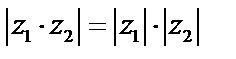, 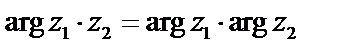. Получили формулу: 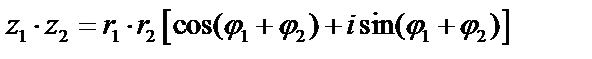. При умножении комплексных чисел, заданных в тригонометрической форме, модули перемножаются, а аргументы складываются.

Полученная формула справедлива и для произведения 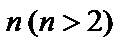комплексных чисел. При этом имеем 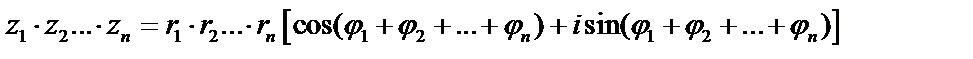. Полагая в равенстве 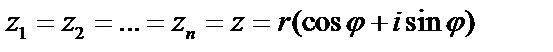, найдем: 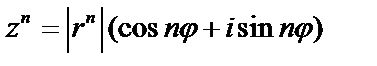, т.е. 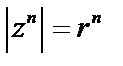; 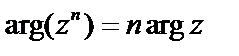. Эта формула называется формулой Муавра.

Деление. Рассмотрим деление двух комплексных чисел, заданных в тригонометрической форме .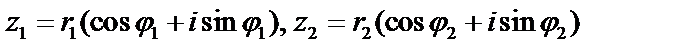

.

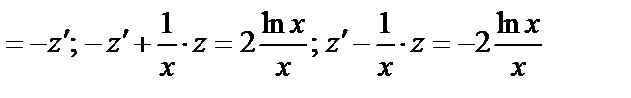
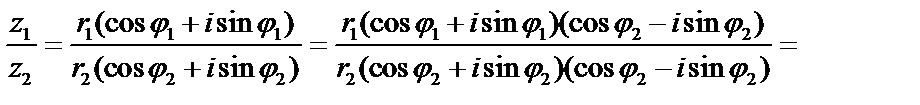
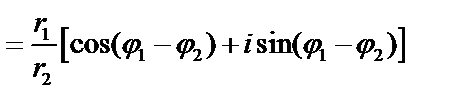Следовательно, 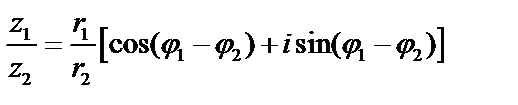, т.е. .

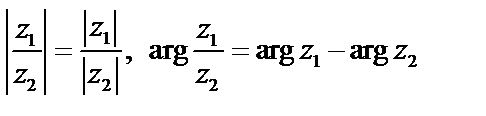При делении комплексных чисел, заданных в тригонометрической форме, модуль частного равен частному их модулей, а из аргумента делимого вычитаем аргумент делителя.

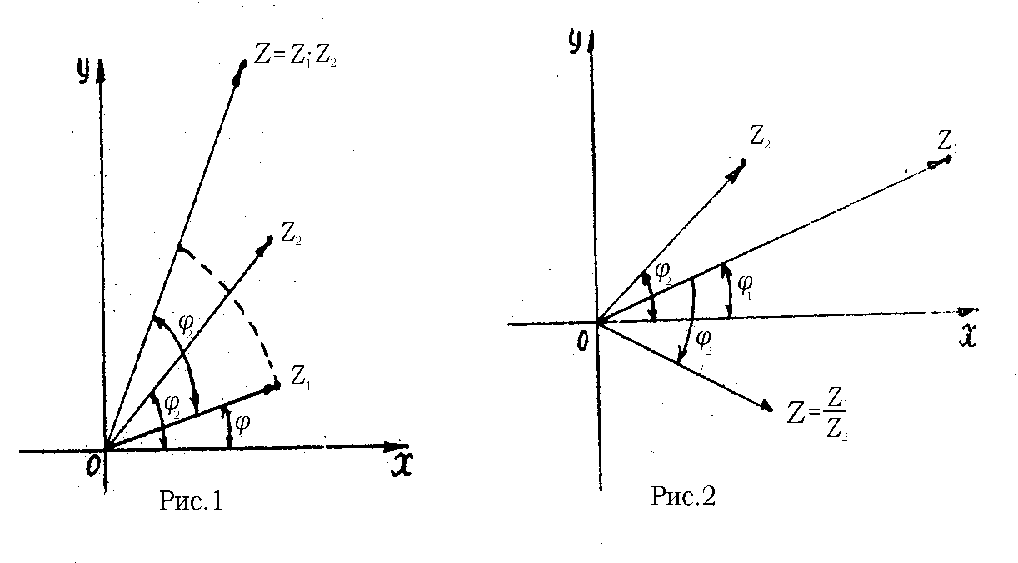
Дадим геометрическую интерпретацию умножения и деления комплексных чисел. Из формулы умножения следует, что при умножении комплексных чисел 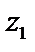на 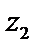вектор OZ, поворачивается около начала 0(0,0) против часовой стрелки на угол 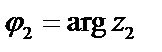и сжимается (растягивается) в 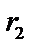раз, если 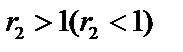(рис.1).

При делении же комплексных чисел 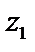на 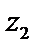, согласно формуле, вектор OZ, поворачивается около точки 0(0,0) по часовой стрелке на угол 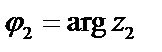и сжимается (растягивается) в 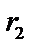раз, если 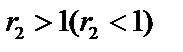(рис.2).

Извлечение корня. Пусть дано комплексное число 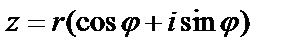. Надо найти комплексное число 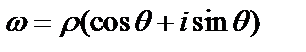., удовлетворяющее условию 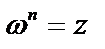. Согласно формуле Муавра, получим: .

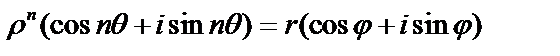Отсюда находим 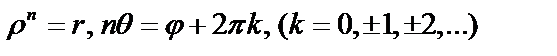или 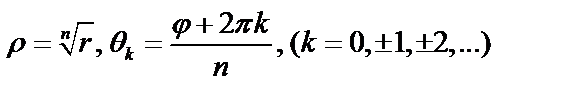Таким образом, имеем 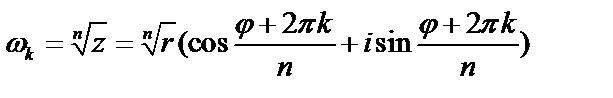,где .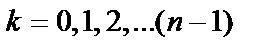

Первые равенства показывают, что модули всех корней 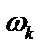одинаковы и расположены на окружности радиуса 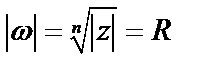с центром в начале координат. Обозначим одно из значений корня с аргументом 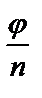, полученное из формулы при k = 0 через 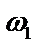; тогда 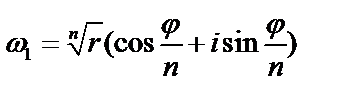Полагая затем 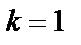, найдем следующее значение корня 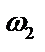с аргументом 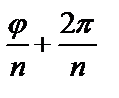: 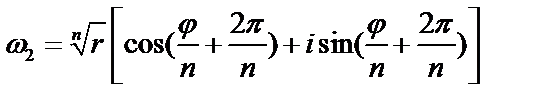; его можно получить из первого значения поворота на угол 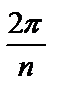. Затем, полагая 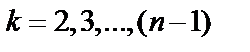, находим все значения корня. Каждое последующее получается из предыдущего поворотом на один и тот же угол .

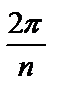Следовательно, все n значений корней 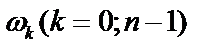делят окружность радиуса 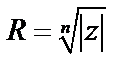на n равных частей, т.е. являются вершинами правильного n – угольника, вписанного в эту окружность.

Пример 4. Вычислить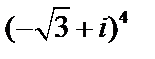

Решение. Получим тригонометрическую форму комплексного числа: 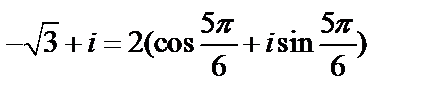.Применяя формулу Муавра для 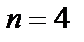, получаем:

.

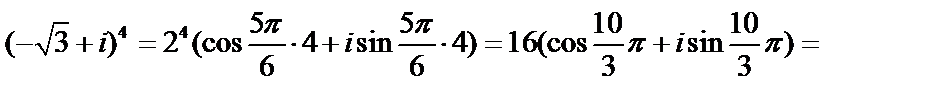
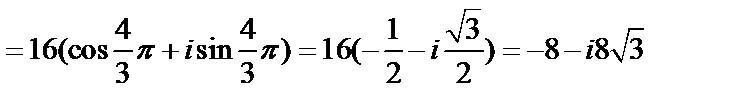Пример 5. Вычислить .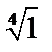

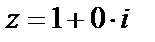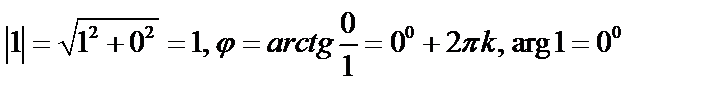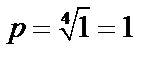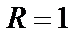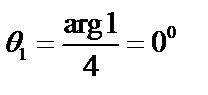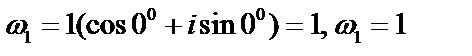Решение. Представим число 1 в тригонометрической форме. Имеем ,тогда по формулам, получим: , т.е. число находится на положительной полуоси ОХ. Из формулы находим , значит, все значения корней лежат на единичной окружности . Далее и . Все значения 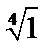лежат в вершинах квадрата, вписанного в единичную окружность 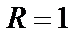, причем одна из вершин этого квадрата – точка (1,0), а остальные значения корней 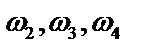можно получить поворотом на угол 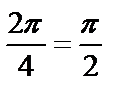первого значения корня , ;

; ;

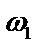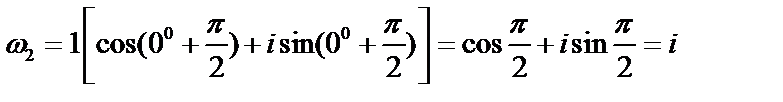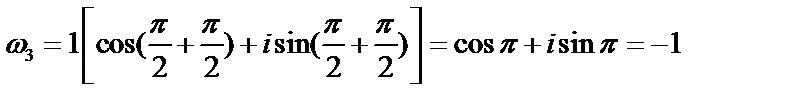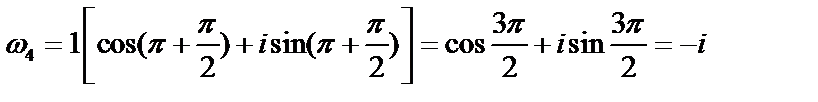Пример 6. Найти все значения .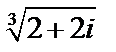

Решение. Представим число 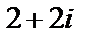в тригонометрической форме. Это число лежит в первой четверти; по формулам находим .

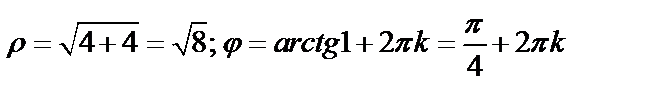Следовательно, 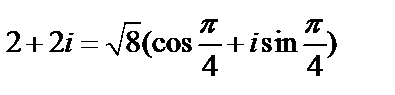По формулам определяем корни: ,

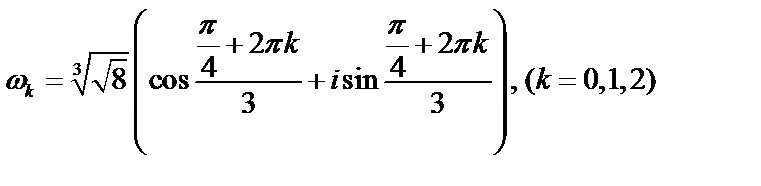отсюда получим:

при ,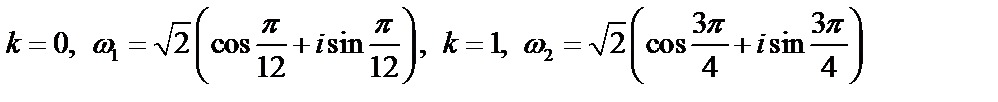

.

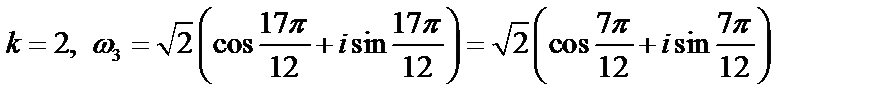12.3. Понятие дифференциального уравнения. Задача Коши

Дифференциальное уравнение – уравнение, связывающее аргумент x,исходную функцию y и её производные. Порядок старшей производной называется порядок дифференциального уравнения.

Всякая 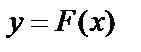– решение, если она обращает его в тождество.

Общее решение дифференциального уравнения n–го порядка содержит n констант 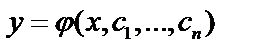, иногда получаем ответ в виде: 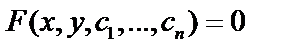это общий интеграл.

Дифференциальное уравнение I -го порядка

Это дифференциальное уравнение вида 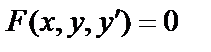, иногда .

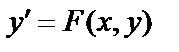Общее решение 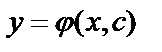, с – произвольная постоянная.

Геометрически общее решение – семейство интегральных кривых.

Если задать точку 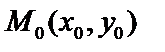, через которую проходить кривая, то тем самым из бесконечного числа кривых выделяется 1 кривая – частное решение.

Аналитически – имеется начальное условие: 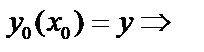из общего решения находится частное. Это задача Коши.

Пример. Решить задачу Коши: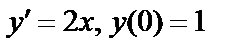

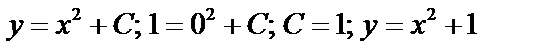– частное решение.

Дифференциальное уравнение первого порядка можно записать 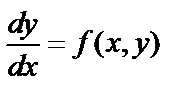или .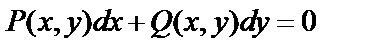

Рассмотрим решение некоторых дифференциальных уравнений первого порядка.

12.4. Дифференциальное уравнение с разделяющимися переменными

Рассмотрим дифференциальное уравнение, 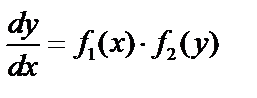, полагая, что 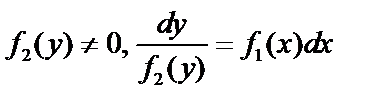. Интегрируя, получим решение: .

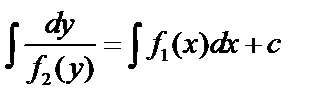Дифференциальное уравнение с разделяющимися переменными можно записать в виде: 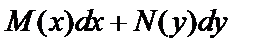. Интегрируем: .

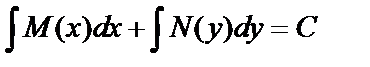Пример:

.

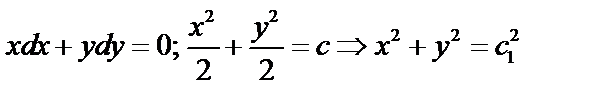Если дифференциальное уравнение записано в виде: 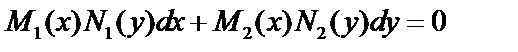и 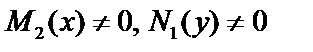, то преобразуем его: 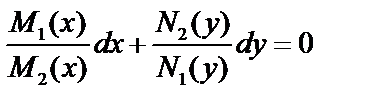Далее интегрируем .

Примеры:

.

,

.

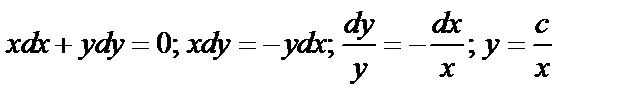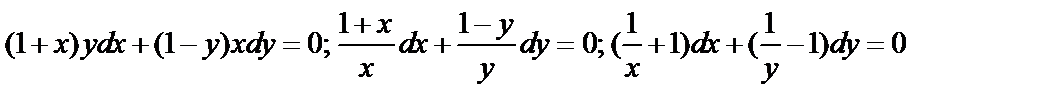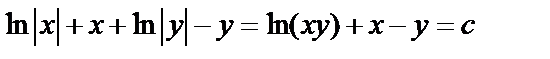12.5.Однородные относительно аргумента и функции дифференциального уравнения

Функция 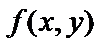называется однородной функцией n-го измерения, если .

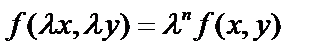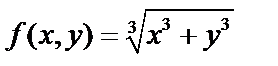1-го измерения, 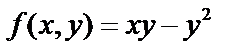– 2-го измерения.

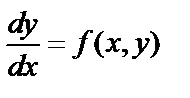называется однородным относительно x и y, если 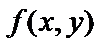однородная функция нулевого измерения.

Решение. По условию: 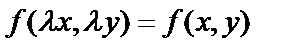. Пусть 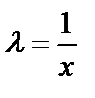тогда 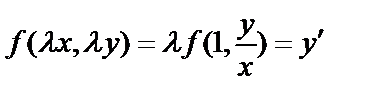. Сделаем подстановку:

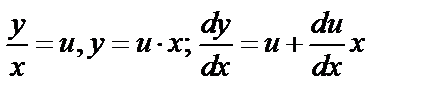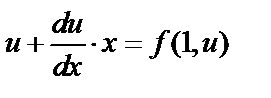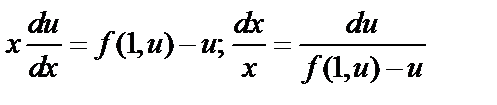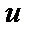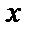подставим в дифференциальное уравнение: Это дифференциальное уравнение с разделяющимися переменными. , далее - интегрируем по и . Подставим вместо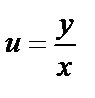

Пример: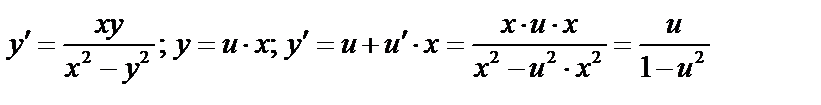

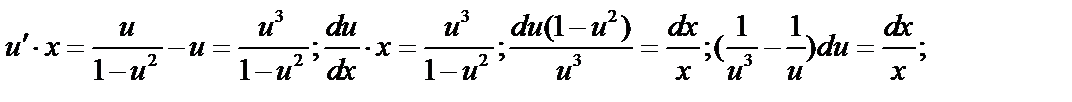интегрируем:

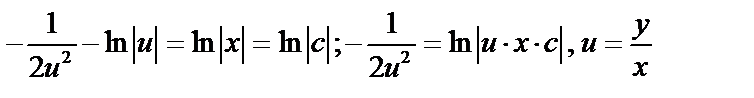, имеем: .

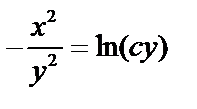12.6. Решение линейного дифференциального уравнения первого порядка методом подстановки

Линейным уравнением первого порядка называется уравнение, линейное относительно 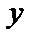и 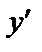. Оно имеет вид: 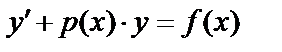. Если 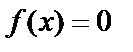, то это однородное уравнение, иначе не однородное.

Будем искать решение в виде 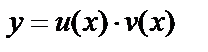, тогда 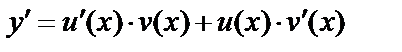, подставим в уравнение: 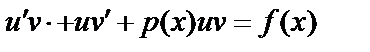, или 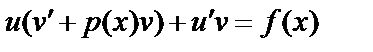Выберем 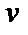такой, чтобы 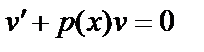, тогда 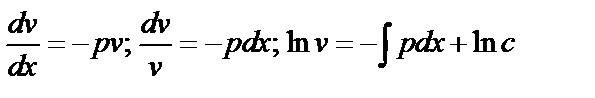, или 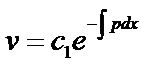, т.к. достаточно отличного от нуля решения, то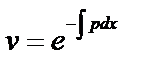 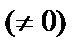. Подставим найденное значение :

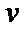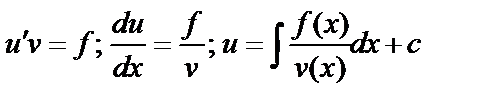окончательно, .

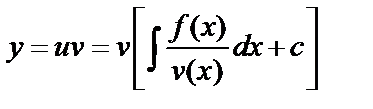Пример: .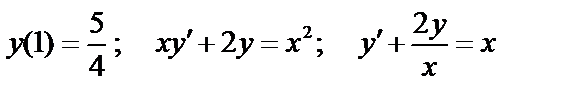

Пусть ; ;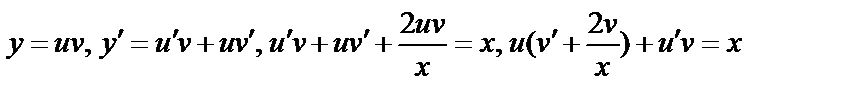

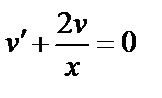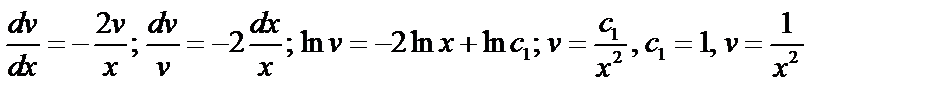. Подставим в исходное: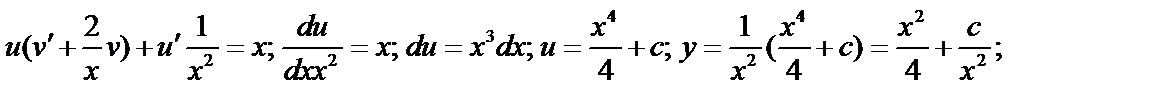 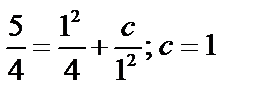, частное решение: .

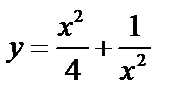12.7. Решение линейного дифференциального уравнения первого порядка методом вариации произвольной постоянной

Найдём решение однородного уравнения: 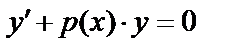, переменные

разделяются: .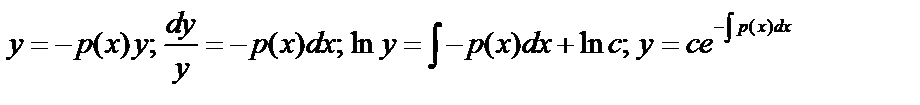

Будем считать, что 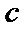- это функция от 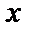: 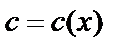, тогда 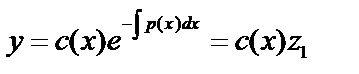(для удобства). Подставим в уравнение:

.

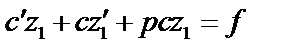
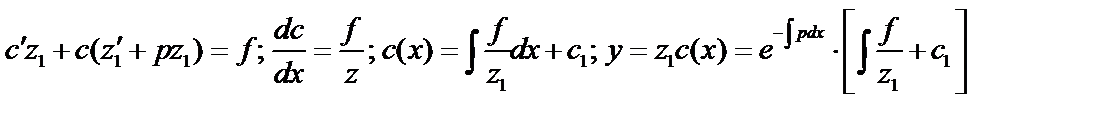Пример:

;

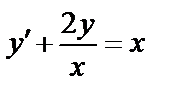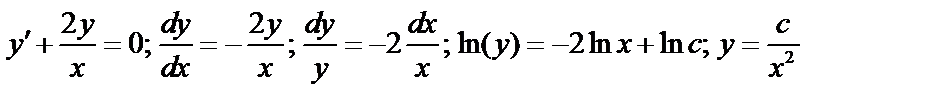; считаем .

;

.

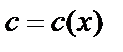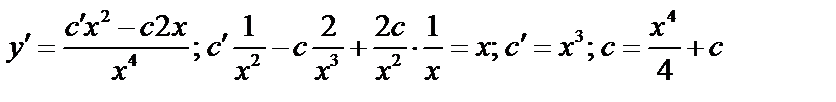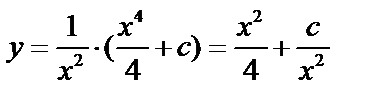12.8. Уравнение Бернулли.

Уравнение Бернулли имеет вид: .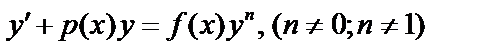

Разделим н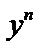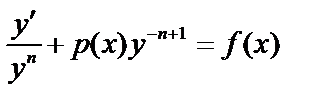а : (а).

Сделаем замену: 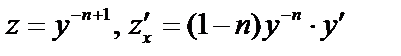подставим в (а):

Это линейное дифференциальное уравнение относительно 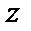: 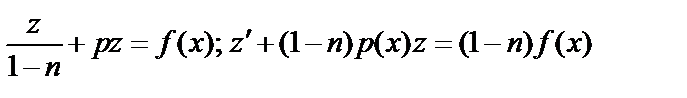. Находим 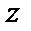, затем находим 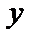(вместо 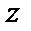подставим ).

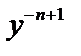Пример:

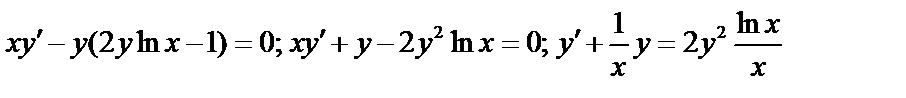-Бернулли!

;

.

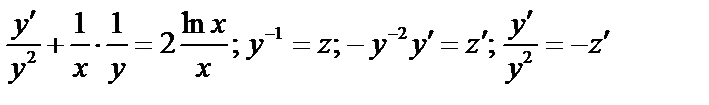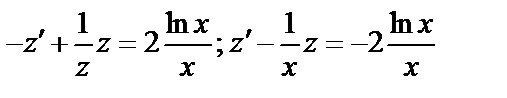линейное относительно :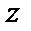

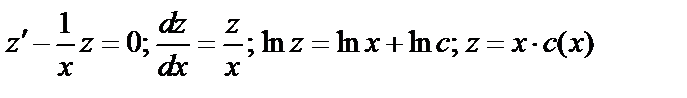методом вариации.

;

.

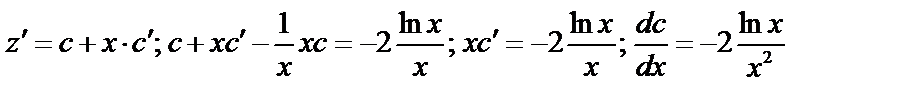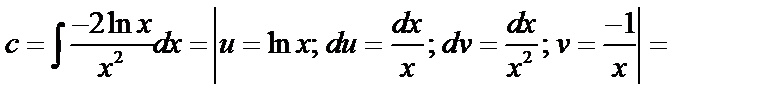
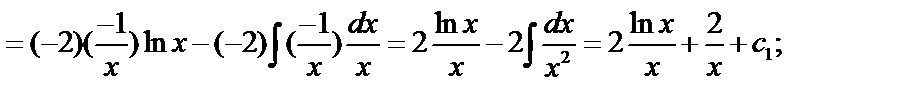
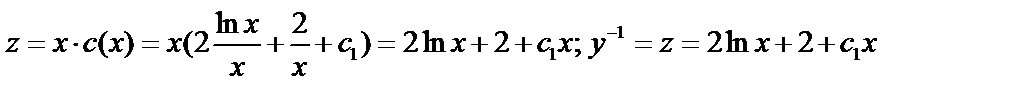12.9. Понижение порядка в дифференциальных уравнениях.

Если искомая функция 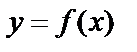есть функция одного независимого переменного, то дифференциальное уравнение называют обыкновенным.

Дифференциальное уравнение порядка

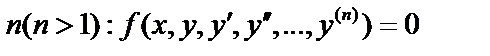. Всякая функция 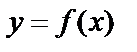определённая

и 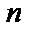раз дифференцируемая, называется решением этого уравнения, если она обращает его в тождество.

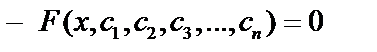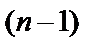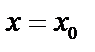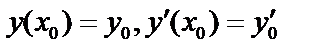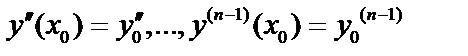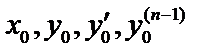Решение . Задача Коши: найти такое решение д.у., чтобы оно само и его производные до порядка при принимали бы заданные значения , где заданные числа, называемые начальными условиями. Задача Коши – значение функции и производных задаются при одном и том же значении .

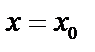Общее решение: если задачу Коши можно решить при любых начальных значениях, то 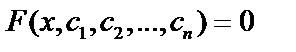– общее решение.

Понижение порядка

I. 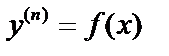. Общее решение – интегрирование 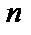раз: .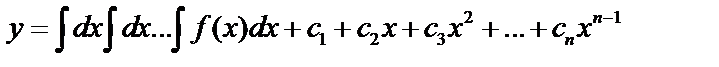

Пример: .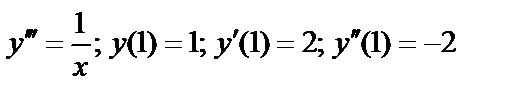

,

.

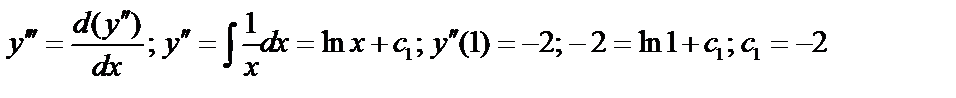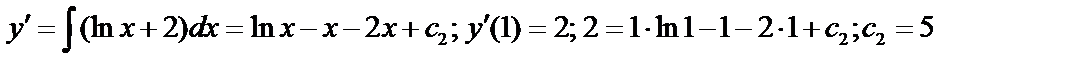
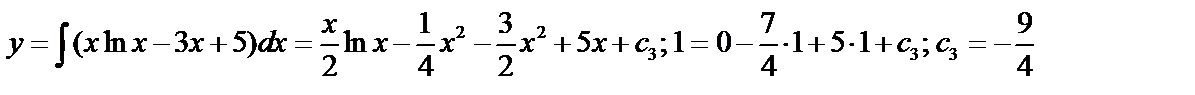
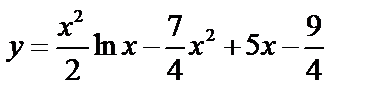II. Уравнения, не содержащие искомой функции 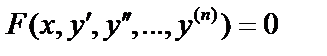. Порядок может быть понижен на 1: 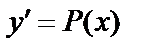получим уравнение 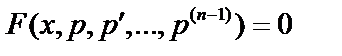. Если уравнение не содержит искомой функции y или её производных до порядка 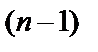, т.е. 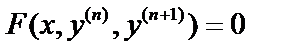, то порядок может быть понижен на 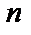единиц: .

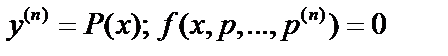Пример: 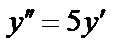; подстановка 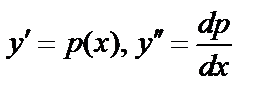; тогда ;

.

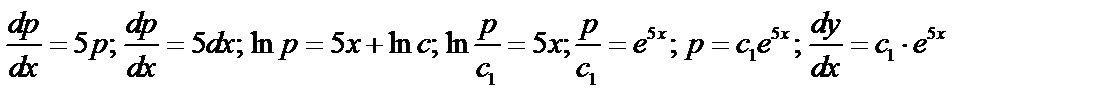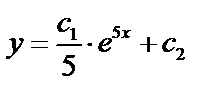III. Уравнения, не содержащие независимой переменной 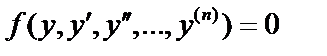. Понижение порядка на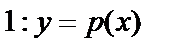

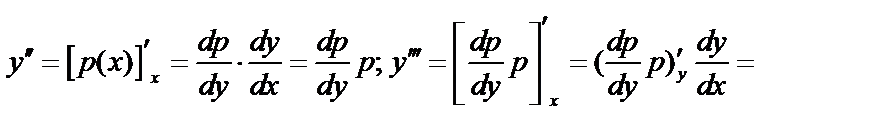
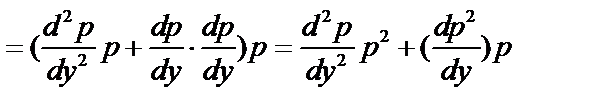
Общее решение уравнения: 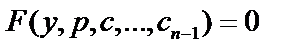; 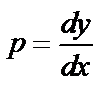- I-го порядка.

Пример: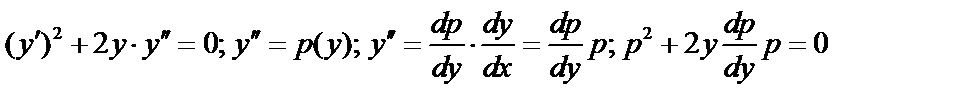

,

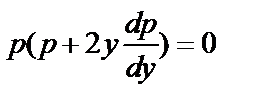а) ;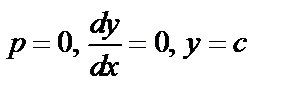

б) ;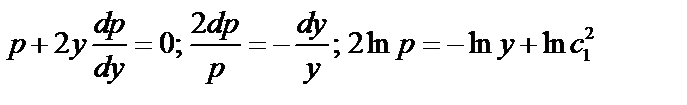

;

.

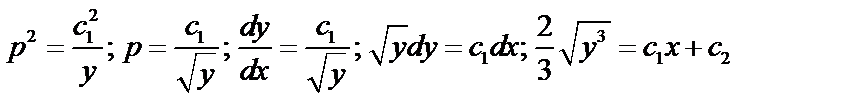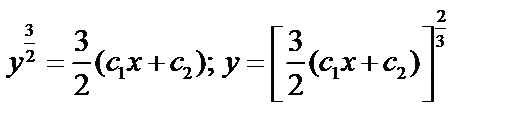12.10. Линейные дифференциальные уравнения второго порядка: свойства решений. Определитель Вронского

Дифференциальное уравнение называется линейным, если оно первой степени относительно искомой функции y и её производных 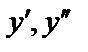и т.д.

Линейное дифференциальное уравнение второго порядка имеет вид:

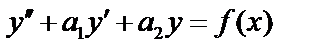(1), где 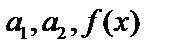- заданные функции от .

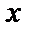Если 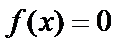, то уравнение называется однородным или уравнением без первой части.

Если 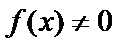то уравнение называется неоднородным или уравнением с правой частью.

Рассмотрим линейное однородное дифференциальное уравнение второго порядка:

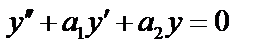
Теорема 1: есл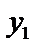и и 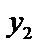–два частных решения (1), то 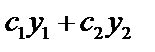– тоже решение.

Определитель Вронского.

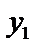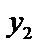Определение. Два решения уравнения (1) и называется линейно независимым на отрезке 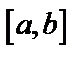, если их отношения на этом отрезке не являются постоянными, т.е. 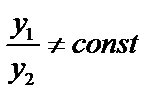. Иначе решения называются линейно зависимыми, тогда .

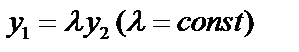Есл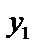и и 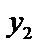есть функции от 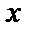, то определитель 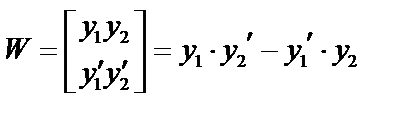называется определителем Вронского.

Теорема 2: если решения 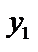и 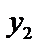– линейно зависимые на отрезке 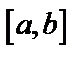, то .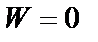

12.11. Линейные дифференциальные уравнения второго порядка: формула Лиувилля.

Теорема 3: Если определитель Вронского 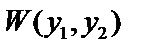, составленный для решени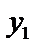й и 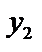уравнения (1), не равен 0 при каком-нибудь значении 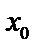на отрезке 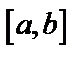, где коэффициенты непрерывны, то он 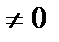ни при каком значении 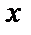на .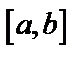

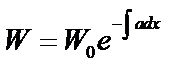-формула Лиувилля.

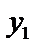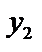Теорема 4: Если и – линейно независимые решения (1), то 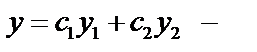общее решение (1).

12.12. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

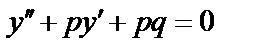(1), 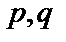– действительные числа. Чтобы найти общий интеграл этого дифференциального уравнения, надо найти два линейно независимых частных решения.

Ищем частные решения в виде: 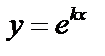тогда 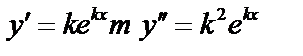. Подставим в (1): 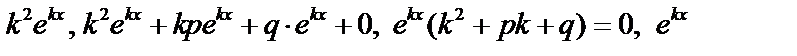, значит, 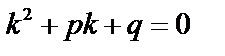. Если 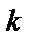удовлетворяет уравнению, то 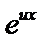– решение. Характеристическое уравнение по отношению к (1). Пусть корни уравнения 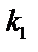и .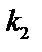

.

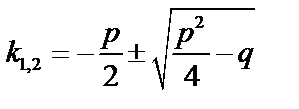Возможны 3 случая:

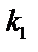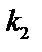1.) и – действительные числа, .

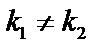2.) 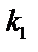= 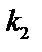– действительные числа.

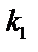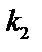3) и ­­– комплексные числа.

1. в этом случае частные решения: 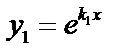и 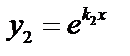, эти решения линейно независимые 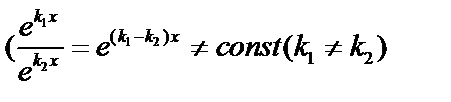.Общее решение: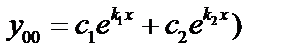

Пример:

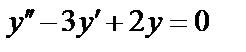. Составим характеристическое уравнение:

.

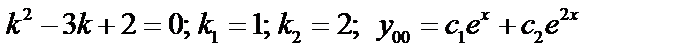2. 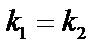. получаем одно частное решение 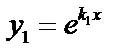. Найдём второе линейно независимое решение 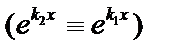. Ищем его в виде: .

;

.

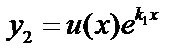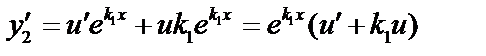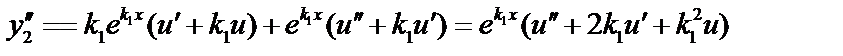Подставим в уравнение (1):

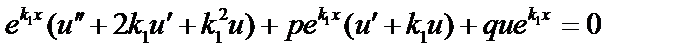или:

.

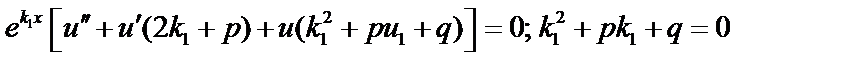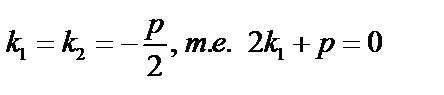значит, .

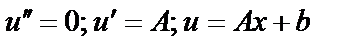Выберем частное решение, 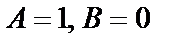, т. е. .

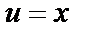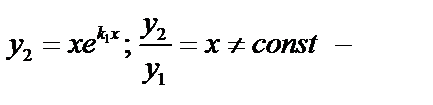линейно независимое, .

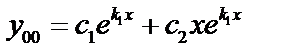Пример: 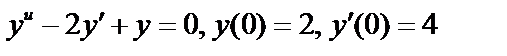Характеристическое уравнение: ,

,

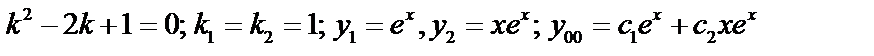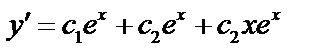тогда 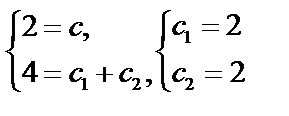. Решение, удовлетворяющее начальным условиям: .

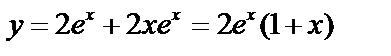3. Комплексные корни. Пусть 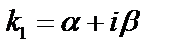, , 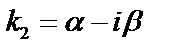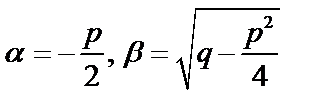Частные решения: 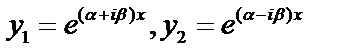. Если какая-либо комплексная функция действительного аргумента 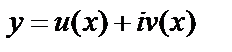удовлетворяет уравнению, то этому уравнению удовлетворяют и функц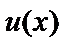ии 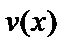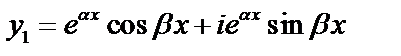и

и 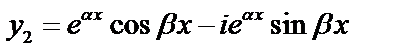. Выберем действительные функци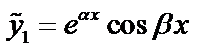и и 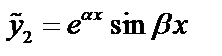которые будут решениями уравнения 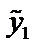и 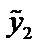линейно независимые: .

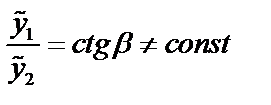Общее решение: .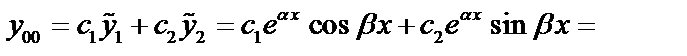

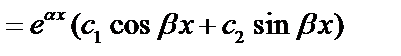Пример: 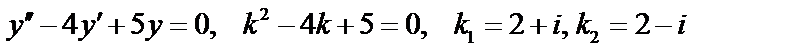, 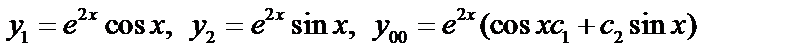- общее решение.

12.13. Неоднородные дифференциальные уравнения с постоянными коэффициентами. Метод вариации произвольной постоянной.

Пусть имеем неоднородное дифференциальное уравнение второго порядка: 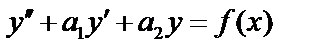. (1)

Теорема 1: Общее решение неоднородного дифференциального уравнения (1) равно сумме какого-либо частного решения этого уравнения 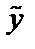и общего решения ( 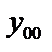) соответствующего однородного уравнения .

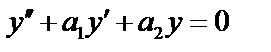Для нахождения частного решения используют метод вариации производных постоянных. В общем решении однородного уравнения 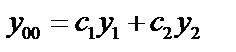(3), считаем 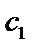и 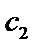как функции от X.

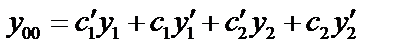Подберём 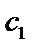и 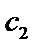так, чтобы 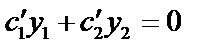тогда 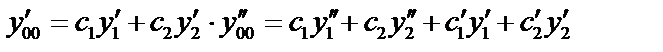. Подставим в (1):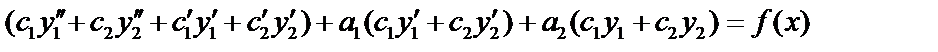 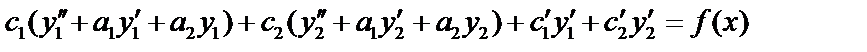если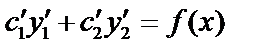

Функция (3) будет решением неоднородного дифференциального уравнения (1), если 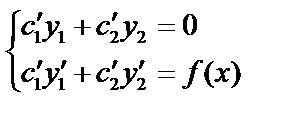(4)

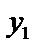и 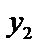_– линейно независимы, 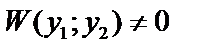, поэтому: .

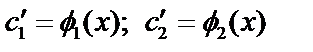Интегрируя, получим: .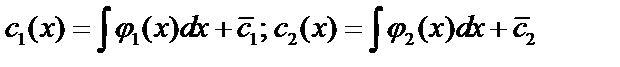

Подставим 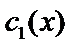и 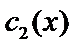в (3) и получим общее решение: .

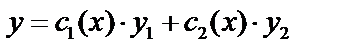Пример:

;

.

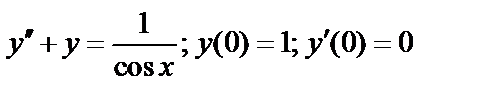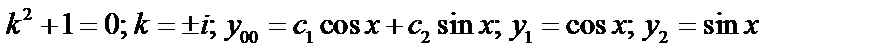Составим систему (4):

; .

;

;

;

.

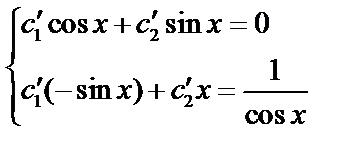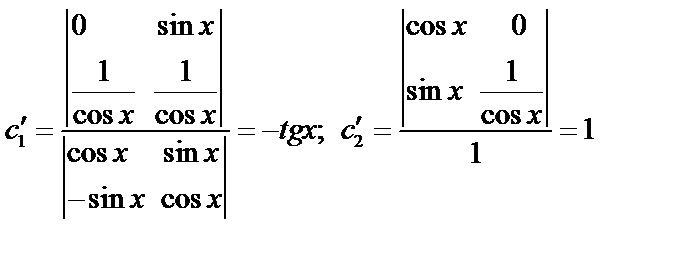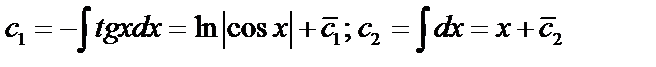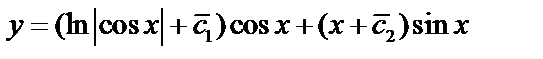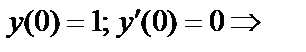
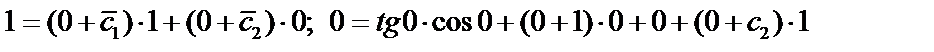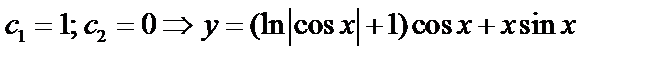12.14. Неоднородные дифференциальные уравнения со специальной правой частью.

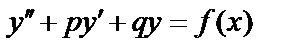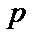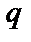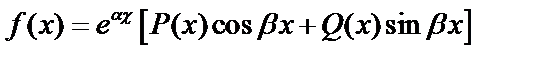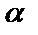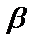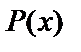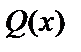Пусть имеем уравнение: где и – действительные числа. Пусть правая часть имеет вид: где и вещественные числа, и – многочлены одной или разных степеней. Если они разной степени, то пусть n – их наибольшая степень. Решение можно определить методом вариации произвольных постоянных, однако можно отыскать решение более простым методом неопределённых коэффициентов.

Рассмотрим два случая:

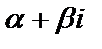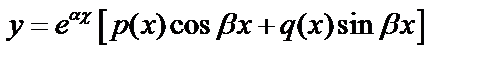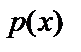1. число не является корнем характеристического уравнения соответствующего однородного д.у. В этом случае частное решение ищем в виде: (1) , где и 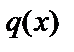– многочлены одной и той же степени, равной наивысшей степен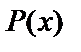и и 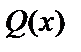. Необходимо определить коэффициенты многочленов 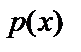и .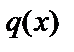

2. Если число 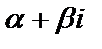является корнем кратности 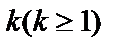характеристического уравнения, то частное решение ищем в виде:

(2) 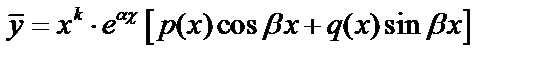. Ищем коэффициенты 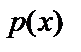и .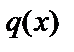

В обоих случаях определяем коэффициенты многочленов так: в данное уравнение подставляем 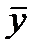и сравниваем коэффициенты при одинаковых степенях x в левой и правой частях равенства. Получаем систему уравнений, из которых определяем коэффициенты многочленов 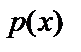и .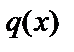

Пример 1:

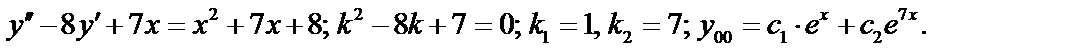В правой части отсутствует множитель 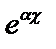, следовательно, 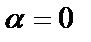и правая часть не содержит 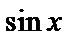и 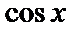, это значит, что 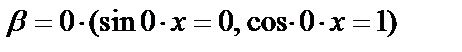. Число 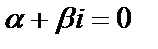не является корнем характеристического уравнения. Частное решение ищем в виде (1), где 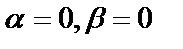, степень многочлена 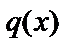– вторая .

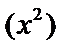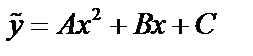. Найти A , B , C. 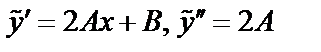Подставим в уравнение:

;

.

.

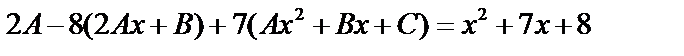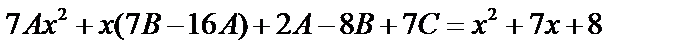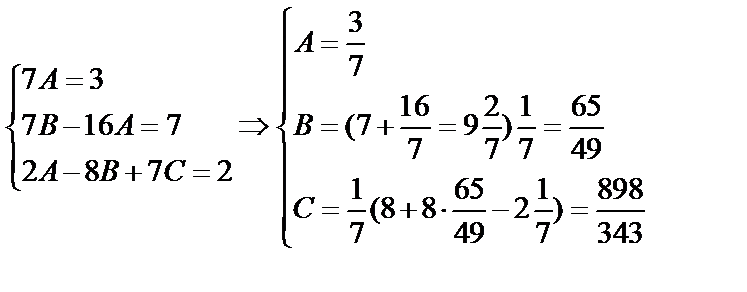
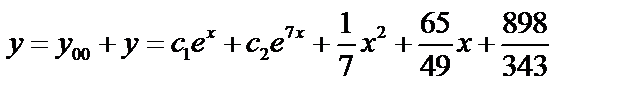Пример 2: ;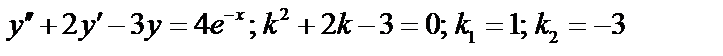

,

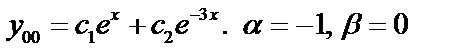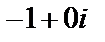не корень, характеристическое уравнение, поэтому .

.

.

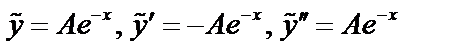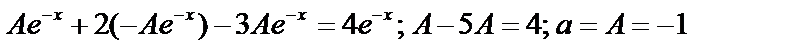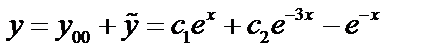Пример 3: 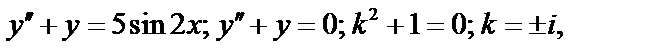- не корень.

,

.

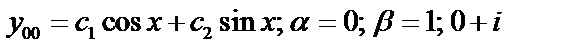
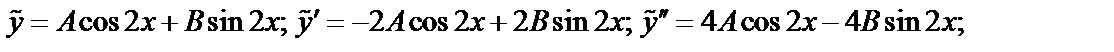
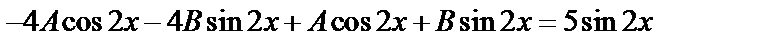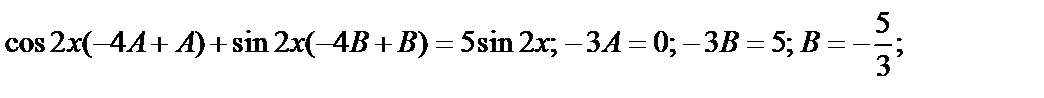
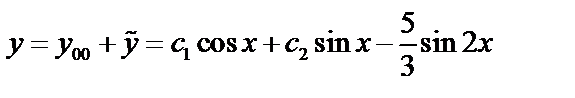Пример 4:

;

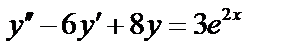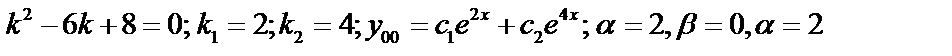- решение характеристического уравнения.

;

.

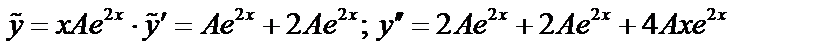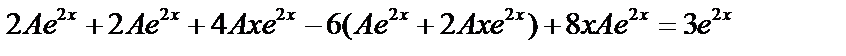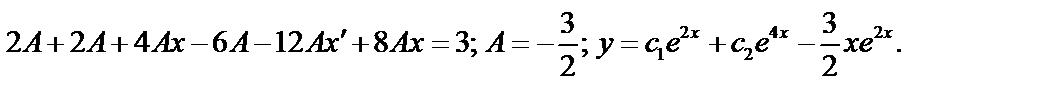
12.15. Системы дифференциальных уравнений.

При решении многих задач требуется найти функции 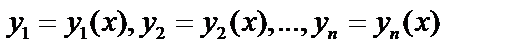, которые удовлетворяют системе дифференциального уравнения , содержащих аргумент x, искомые функции 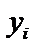и их производные.

Рассмотрим систему дифференциального уравнения первого порядка:

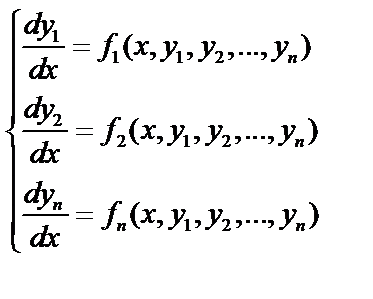(1) 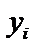– искомая функция, x – аргумент.

Система называется нормальной, если в левой части стоят производные, а правые части их не содержат.

Проинтегрировать систему – найти функции 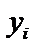, удовлетворяющие системе уравнений (1) и начальным условиям 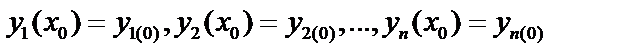. (2)

Дифференцируем по x первое уравнение системы:

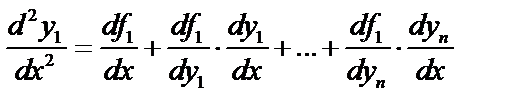. Заменив выражение 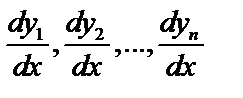их выражениями 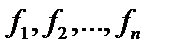из уравнений (1), получим 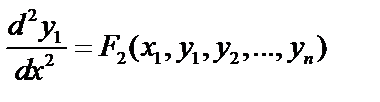. Далее снова дифференцируем по x полученное уравнение:

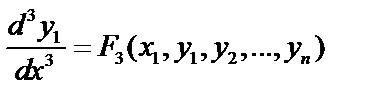, продолжая далее, получим уравнение:

.

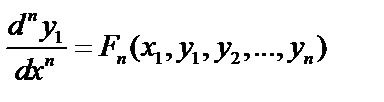Итак, получена система:

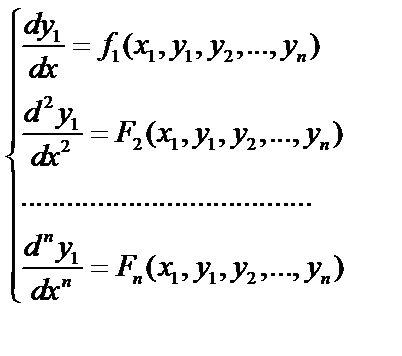(3)

Из первых 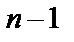уравнений определяем 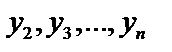, выразив их через 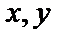и производные :

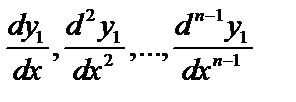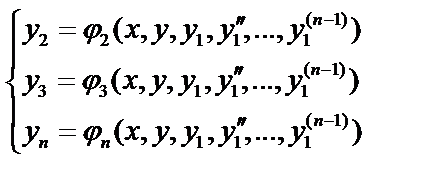(4)

Подставляя эти выражения в последние из уравнений (3), получим уравнение n-го порядка для определения :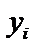

(4_a) 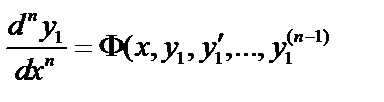Решая его, определим 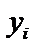: 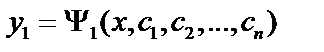. Дифференцируя 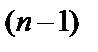раз, найдём производные 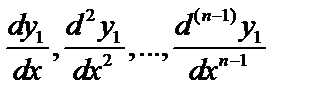как функции 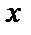, 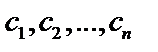. Подставляя эти функции в (4) определим .

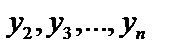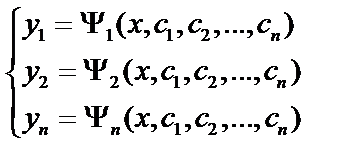(5)

Далее обычным образом определяем с помощью начальных условий.

Замечание 1. Если система (1) линейна относительно искомых функций, то уравнение (4а) будет линейным.

Пример:

Проинтегрировать систему .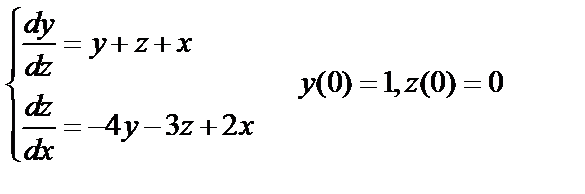

Дифференцируем

1^-е уравнение: .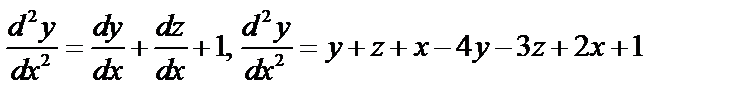

или 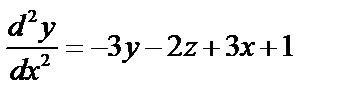. Из 1^го уравнения системы выразим z: 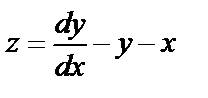и подставляем в полученное уравнение: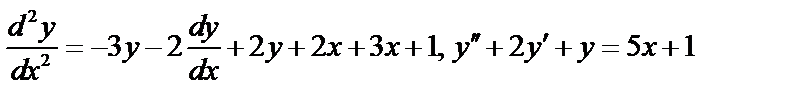

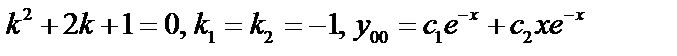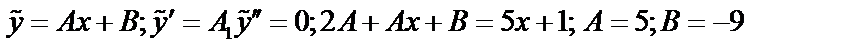. , тогда

.

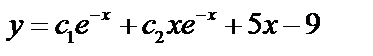Ищем 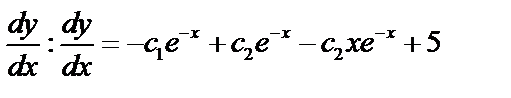, тогда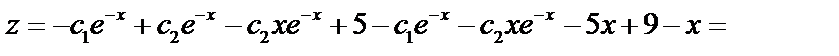

.

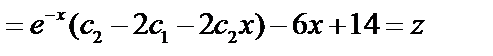Найдём 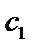и 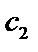так, чтобы удовлетворялись начальные условия:

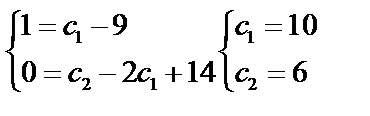Решение, удовлетворяющее начальным условиям, имеет вид:

.

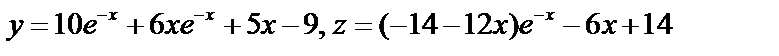Замечание 2. Мы предполагали, что из первых 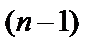уравнений системы (3) можно определить функции 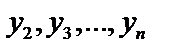. Может случиться, что переменные 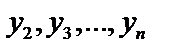, исключаются не из n , а из меньшего числа уравнений. Тогда для определения y мы получаем уравнение, порядок которого ниже n.

Библиографический список

Основной

1.Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Наука, 1975. -236 с.

2. Клетеник Д.В. Сборник задач по аналитической геометрии.- С.-Пб.: Профессия, 2003.-224 с.

3. Пискунов, Н. С. Дифференциальное и интегральное исчисления. Т. 1, 2- М.: Интеграл-Пресс, 2000, 2001. (любого другого года издания)

4. Задачи и упражнения по математическому анализу для втузов. /Под ред. Б. П. Демидовича.- М. : Астрель, 2001,2004.

5. Бермант А.Ф. Краткий курс математического анализа для втузов. – М.:Физматлит, 2003.-720 с.

6. Амосов А.А. Вычислительные методы для инженеров / А.А. Амосов, Ю.А. Дубинский, Н.В. Копченова. – М.: Высш. школа,1994.-231 с.

Дополнительный

7.Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – М.: Наука, 1988. – 224с.

8.Бугров Я.С. Никольский С.М. Дифференциальное и интегральное исчисление. – М.: Наука, 1988. – 432 с.

9.Шипачев И.С. Высшая математика. – М.: Высшая школа, 1990. – 480 с.

Содержание

1. Определители и матрицы………………………………………….2

2. Системы линейных алгебраических уравнений ………….……..10

3. Векторы………………………………………………………….…15

4. Аналитическая геометрия…………………………………………21

5. Функции……………………………………………………………29

6. Пределы и непрерывность…………………………………….….33

7. Производная и дифференциал……………………………………39

8. Основные теоремы дифференциального исчисления……….….48

9. Приложения производной……………………………………..….49

10. Неопределенный интеграл………………………………………52

11. Определенный интеграл…………………………………………64

12. Дифференциальные уравнения …………………………….…..76