Глава 11. Определенный интеграл
11.1.Понятие определенного интеграла и его свойства
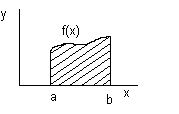
Пусть 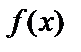 – непрерывная на отрезке
– непрерывная на отрезке 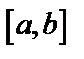 неотрицательная функция.
неотрицательная функция.
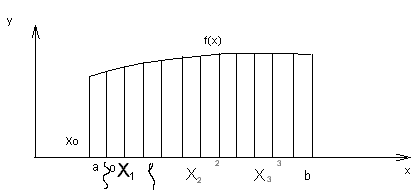
Определим площадь криволинейной трапеции – фигуры, ограниченной прямыми 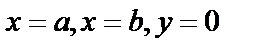 и графиком функции
и графиком функции 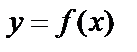
Разобьем 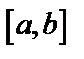 на n частей точками
на n частей точками 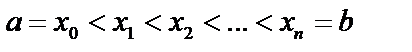 , выберем на каждом из частичных отрезков
, выберем на каждом из частичных отрезков 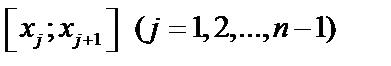 по произвольной точке
по произвольной точке 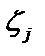 определим значение функции
определим значение функции 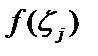 (в этих точках) и составим сумму:
(в этих точках) и составим сумму: 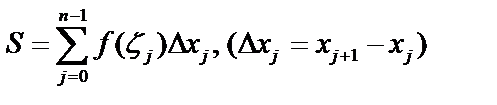 .
.
Эта сумма равна сумме площадей  прямоугольников. Устремим
прямоугольников. Устремим 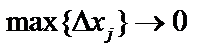 Если при этом
Если при этом 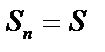 , и
, и 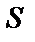 не зависит от способа разбиения и выбора точек
не зависит от способа разбиения и выбора точек 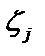 , то величина
, то величина 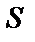 называется площадью данной криволинейной трапеции:
называется площадью данной криволинейной трапеции: 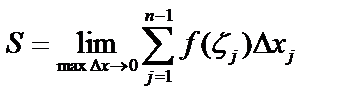 .
.
Каждая криволинейная трапеция, соответствующая непрерывной функции 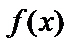 ,имеет площадь
,имеет площадь 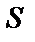 .
.
Указанный предел называется определённым интегралом и обозначается: 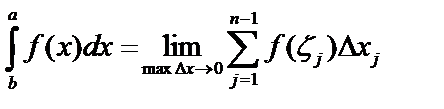 .
.
Числа 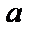 и
и 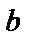 называются нижним
называются нижним 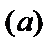 и верхним
и верхним 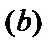 пределами интегрирования,
пределами интегрирования, 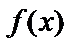 – подынтегральная функция,
– подынтегральная функция, 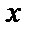 – переменная интегрирования.
– переменная интегрирования.
Определенный интеграл – это число.
Вычисление определённого интеграла по определению можно осуществить с помощью компьютера, однако на практике используют формулу Ньютона – Лейбница.
Пусть задана непрерывная на 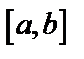 функция
функция 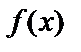 и пусть
и пусть 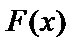 – ее первообразная. Тогда
– ее первообразная. Тогда 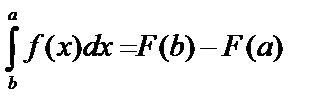 или
или 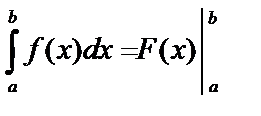 – определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего и нижнего пределов.
– определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего и нижнего пределов.
Определенный интеграл с переменным верхним пределом: 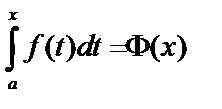 – функция
– функция 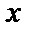 .
.
Если 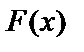 – первообразная для
– первообразная для 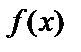 , то
, то 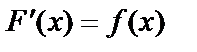 и по формуле Ньютона – Лейбница:
и по формуле Ньютона – Лейбница: 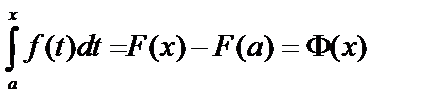 . Дифференцируем:
. Дифференцируем: 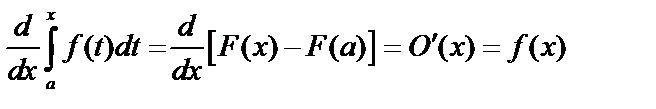 – производная по верхнему пределу равна подынтегральной функции.
– производная по верхнему пределу равна подынтегральной функции.
Свойства определённого интеграла
1. 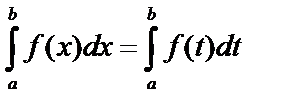 – не зависит от значения переменной интегрирования.
– не зависит от значения переменной интегрирования.
2. 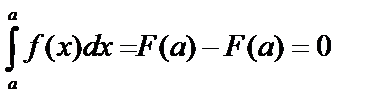 .
.
3. 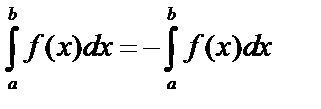 .
.
4.Для любых чисел a, b, c: 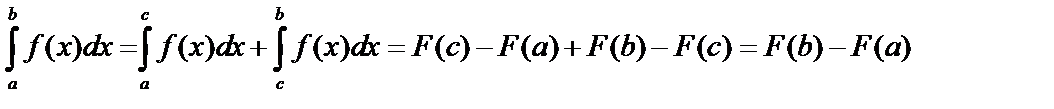 .
.
5. 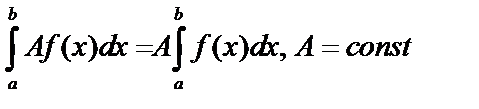 .
.
6. 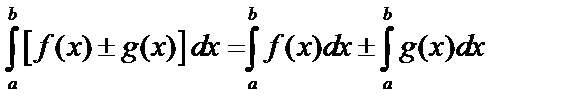 .
.
7. Если 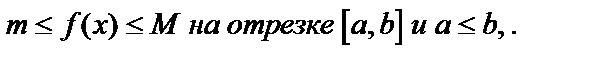
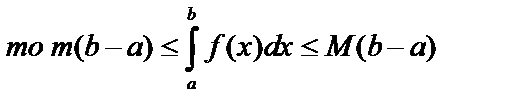
8. 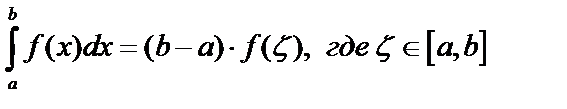 – теорема о среднем.
– теорема о среднем.
Пример: 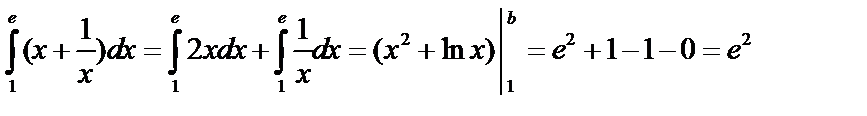 .
.
11.2. Интегрирование по частям и замена переменной в определенном интеграле
Пусть 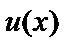 и
и 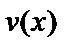 – две непрерывные дифференцируемые функции на отрезке
– две непрерывные дифференцируемые функции на отрезке 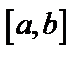 , тогда
, тогда
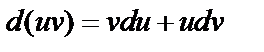 . Проинтегрируем равенство от a до b:
. Проинтегрируем равенство от a до b:
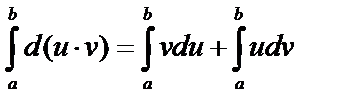 , имеем:
, имеем: 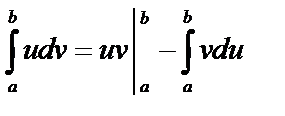 – формула интегрирования по частям.
– формула интегрирования по частям.
Пример. 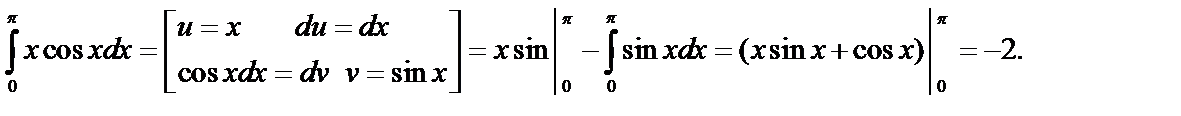
Замена переменной в определённом интеграле
Пусть дан интеграл 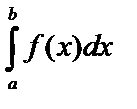 , где
, где 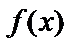 непрерывная функция на
непрерывная функция на 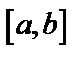 . Введем новую переменную по формуле
. Введем новую переменную по формуле 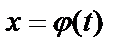 . Если
. Если 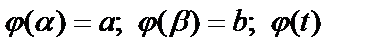 и
и 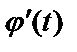 непрерывны на
непрерывны на 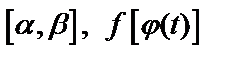 непрерывна на
непрерывна на 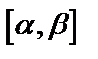 , то:
, то: 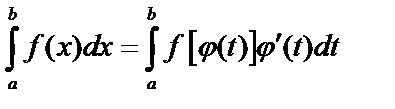 .
.
11.3. Несобственные интегралы с бесконечными пределами
Пусть функция 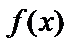 определена и непрерывна при всех
определена и непрерывна при всех 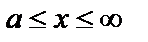 .
.
Тогда несобственный интеграл 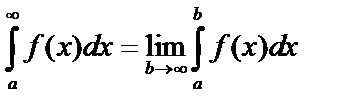 . Если предел существует, то интеграл существует или сходится, если предел не существует, то интеграл расходится (не существует), т.е. не имеет конечного значения.
. Если предел существует, то интеграл существует или сходится, если предел не существует, то интеграл расходится (не существует), т.е. не имеет конечного значения.
Геометрический смысл: 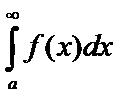 выражает площадь бесконечной области, заключенной между линиями
выражает площадь бесконечной области, заключенной между линиями 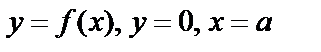 .
.
Аналогично, 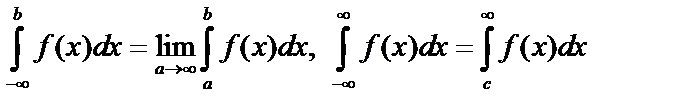 .
.
Для последнего равенства должны существовать оба интеграла, с – число.
Пример 1. Исследовать на сходимость несобственный интеграл: 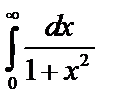 .
.
y
0 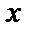
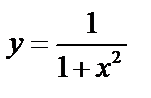
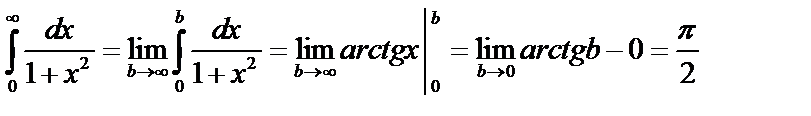 .
.
Пример 2. При каких значениях параметра α интеграл 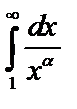 сходится и при каких расходится?
сходится и при каких расходится?
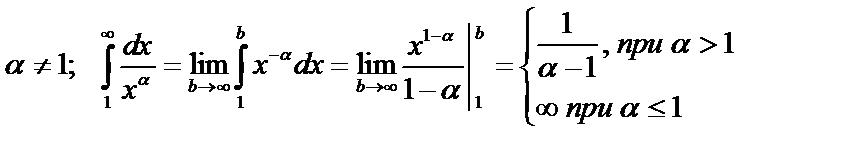 .
.
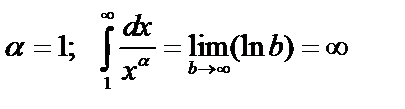
Пример 3. 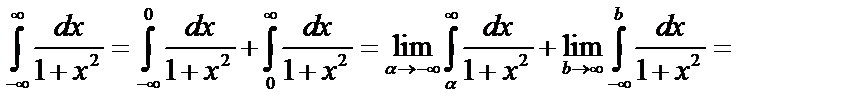
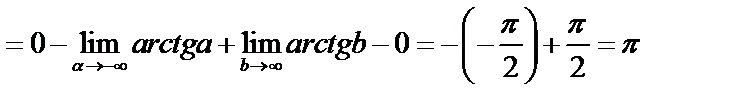 .
.
Если требуется установить, сходится ли данный интеграл или расходится, удобно применять теоремы:
1. Если для всех 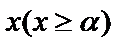 выполняется неравенство
выполняется неравенство 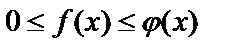 и если
и если 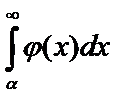 сходится, то
сходится, то 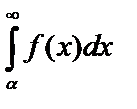 тоже сходится и
тоже сходится и 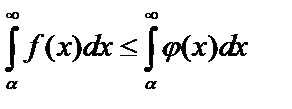 .
.
2. Если для всех 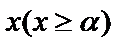 :
: 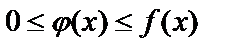 причем
причем 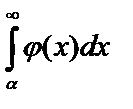 расходится, то и
расходится, то и 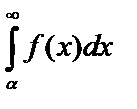 расходится.
расходится.
3. Если 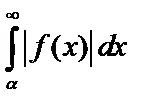 сходится, то и
сходится, то и 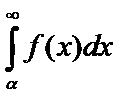 сходится.
сходится.
Пример 4. Сходится ли 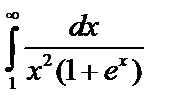 ?
?
При 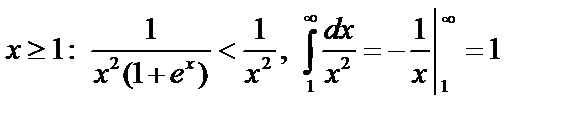 , поэтому (т.1)
, поэтому (т.1) 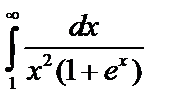 тоже сходится и < 1.
тоже сходится и < 1.
Пример 5. Исследовать 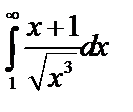 .
.
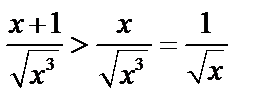 . Но
. Но 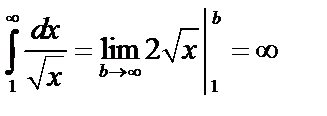 – расходится, поэтому рассматриваемый интеграл тоже расходится.
– расходится, поэтому рассматриваемый интеграл тоже расходится.
Пример 6. Исследовать 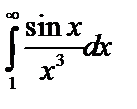 на сходимость.
на сходимость.
Подынтегральная функция знакопеременная. 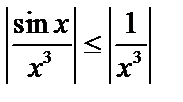 Но
Но 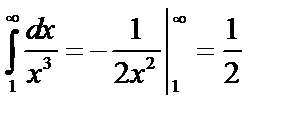 , значит, интеграл
, значит, интеграл 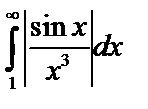 сходится, и по т.3 сходится и
сходится, и по т.3 сходится и 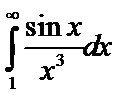 .
.
11.4. Несобственные интегралы от функций, имеющих разрыв
Пусть функция 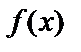 определена и непрерывна при
определена и непрерывна при 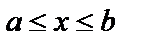 , а при
, а при 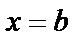 функция либо не определена, либо терпит разрыв. В этом случае нельзя говорить об
функция либо не определена, либо терпит разрыв. В этом случае нельзя говорить об 
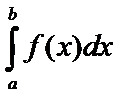 , как о пределе интегральной суммы, поскольку этот предел может не существовать.
, как о пределе интегральной суммы, поскольку этот предел может не существовать.
Интеграл 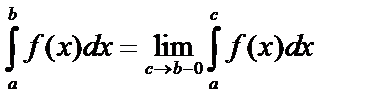 Если предел существует, то интеграл сходится, иначе – расходится.
Если предел существует, то интеграл сходится, иначе – расходится.
Если функция имеет разрыв при 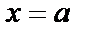 , то
, то 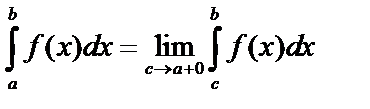 – аналогично, если предел существует, то интеграл сходится, иначе – расходится.
– аналогично, если предел существует, то интеграл сходится, иначе – расходится.
Если 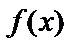 имеет разрыв в точке
имеет разрыв в точке 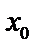 внутри отрезка
внутри отрезка 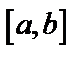 , то
, то 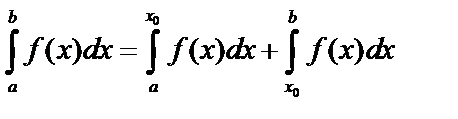 – существует, если существуют оба интеграла в правой части.
– существует, если существуют оба интеграла в правой части.
Пример 1. Исследовать сходимость 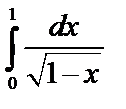 .
.
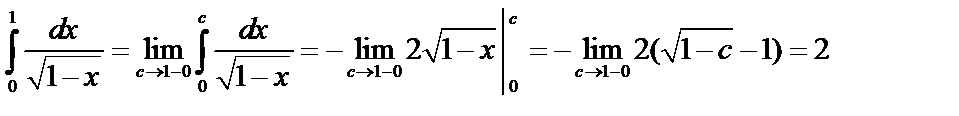 – сходится.
– сходится.
Пример 2. 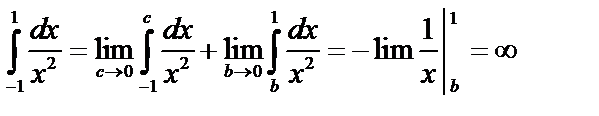 – интеграл расходится.
– интеграл расходится.
Геометрические приложения определенного интеграла
11.5. Вычисление площади плоской фигуры
а) Площадь плоской фигуры 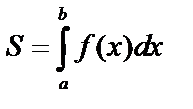 , если
, если 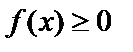
Если 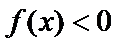 на интервале интегрирования, то рассматривают интеграл от модуля (или изменяют знак).
на интервале интегрирования, то рассматривают интеграл от модуля (или изменяют знак). 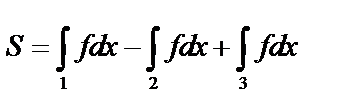 или
или 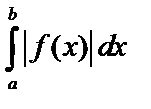 .
.
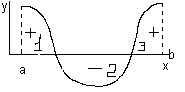
Пример 1. Найти площадь фигуры, ограниченной графиком 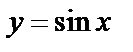 и осью абсцисс, если
и осью абсцисс, если 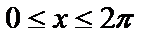 .
.
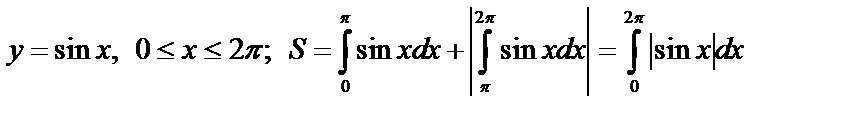
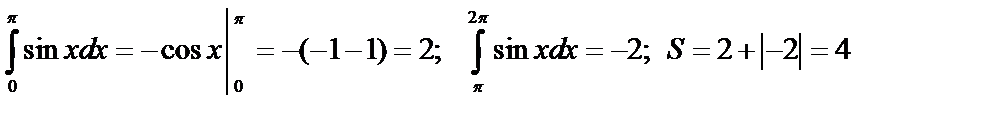 .
.
Более удобной является формула: 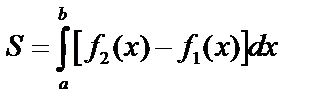 где
где 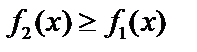 .
.
y
f2(x)
f1(x)
0 х
Пример 2. Найти площадь, ограниченной параболой 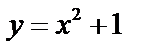 и прямой
и прямой 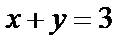 .
.
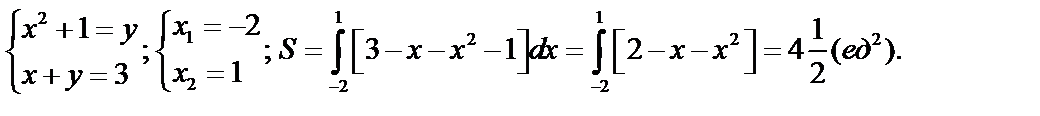
б) Пусть функция задана в параметрической форме: 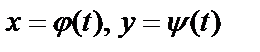 .
.
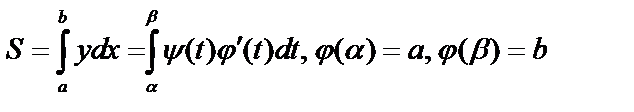 .
.
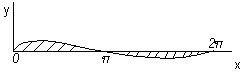
Пример 3. Вычислить площадь одной арки циклоиды 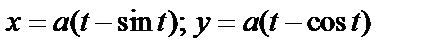 .
.
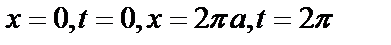 .
.
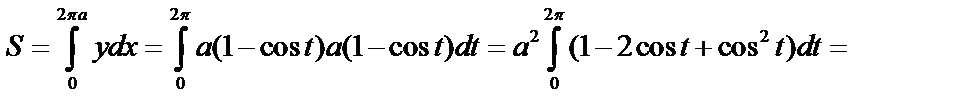
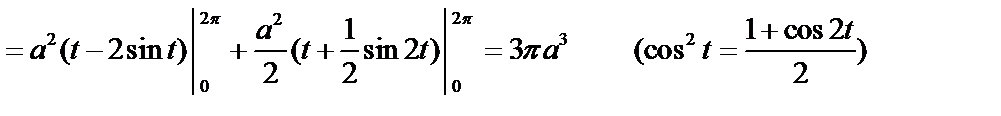 .
.
M
N
0  x
x
в) Если кривая задана в полярных координатах: 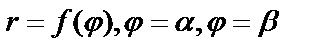 .
.
Разобьем данную площадь радиус – векторами 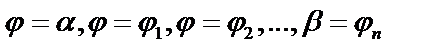 на n частей. Пусть углы между радиус – векторами равны
на n частей. Пусть углы между радиус – векторами равны 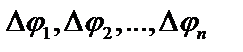 Площадь
Площадь 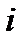 сектора:
сектора: 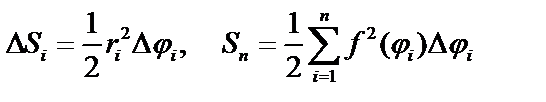 .
.
Площадь: 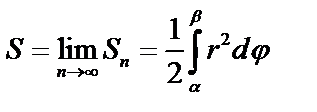 .
.
Пример 4. Найти S, ограниченную кардиоидой: 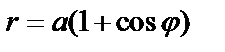 .
.
Вычислить половину площади:
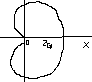
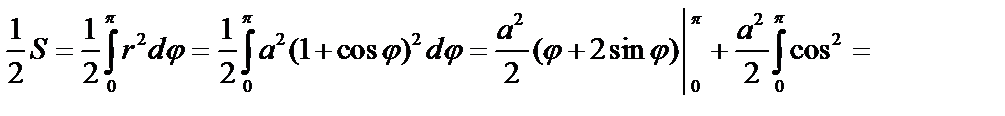
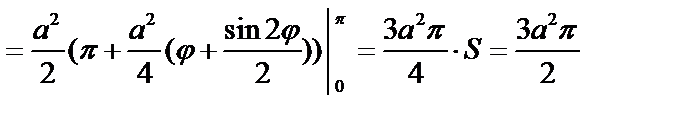 .
.
11.6. Длина дуги кривой
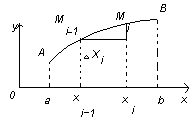
а) Пусть кривая задана уравнением 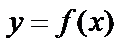 . Возьмем на
. Возьмем на 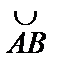 точки
точки 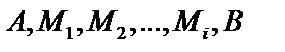 , и проведем хорды, которые обозначим
, и проведем хорды, которые обозначим 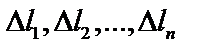 . Получим ломанную
. Получим ломанную 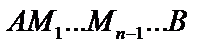 , вписанную в дугу
, вписанную в дугу 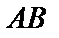 . Длина ломаной:
. Длина ломаной: 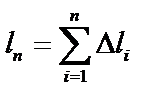 . Длина дуги – предел:
. Длина дуги – предел: 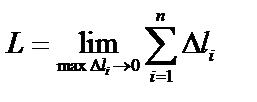 . Если на отрезке
. Если на отрезке 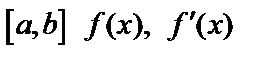 непрерывны, то этот предел существует. Пусть
непрерывны, то этот предел существует. Пусть 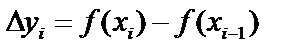 , тогда
, тогда 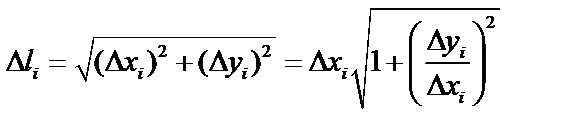 . По теореме Лагранжа
. По теореме Лагранжа 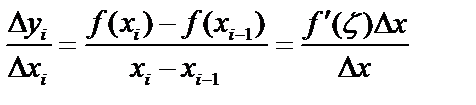 ,
, 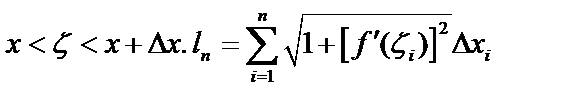 , по условию,
, по условию, 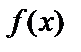 и
и 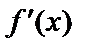 – непрерывны, поэтому существует предел интегральной суммы, который равен определенному интегралу:
– непрерывны, поэтому существует предел интегральной суммы, который равен определенному интегралу:
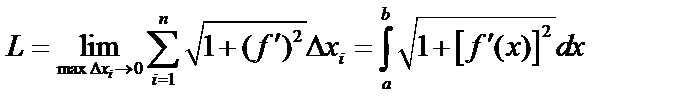 .
.
Пример. Найти длину дуги кривой 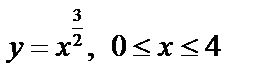 .
.
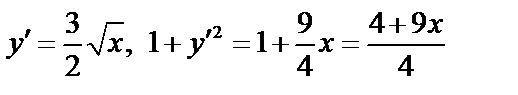
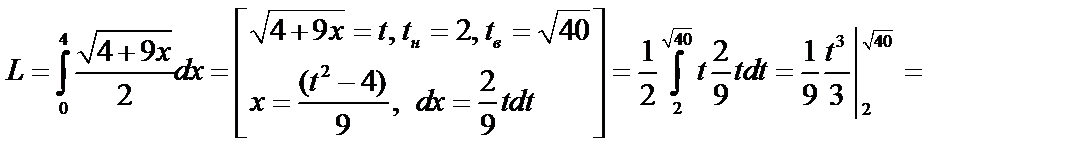
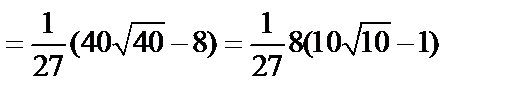 .
.
б) Если кривая задана параметрически: 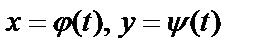 то длина дуги
то длина дуги
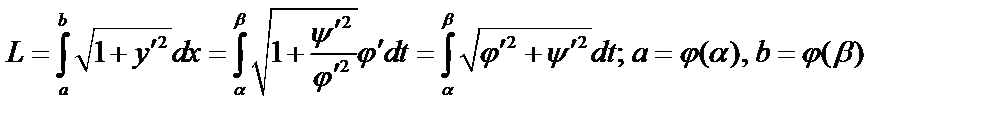 .
.
в) Пусть кривая задана в полярных координатах: 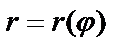 тогда
тогда 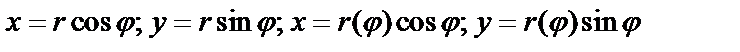 .
.
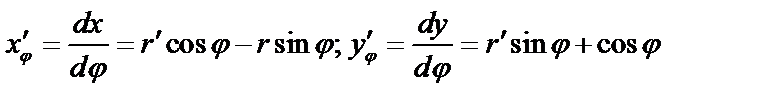 ;
;
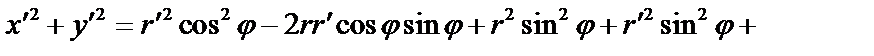
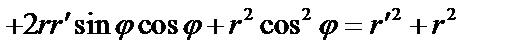 ;
;
тогда 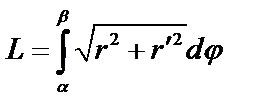 .
.
Пример. Найти длину дуги кардиоиды: 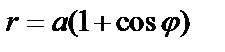 .
.
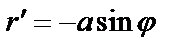 ;
; 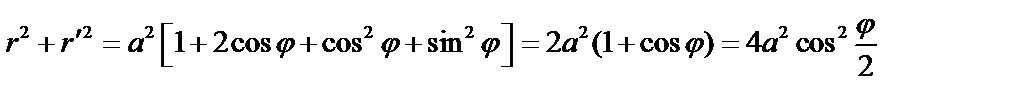 ;
;
длина дуги: 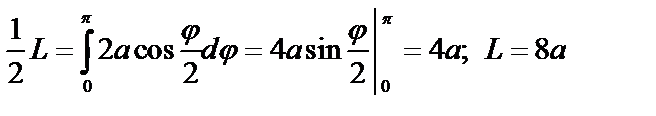 .
.
11.7.Вычисление объема и площади поверхности вращения.
Пусть имеется тело, для которого известна площадь сечения, перпендикулярного оси ох, т.е. 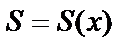 . Проведем плоскости, перпендикулярные оси ох. Они разобьют тело на слои,
. Проведем плоскости, перпендикулярные оси ох. Они разобьют тело на слои, 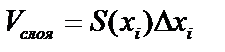 (цилиндр), тогда
(цилиндр), тогда 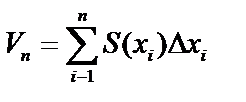 . Переходя к пределу:
. Переходя к пределу: 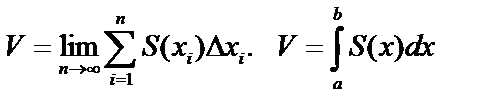 .
.
Объем тела вращения:
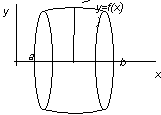
Если ось вращения – ось OY, то объем тела вращения: 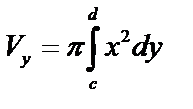 .
.
Если ось вращения – ось OX, то объем тела вращения: 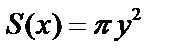 и
и 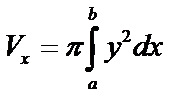 .
.
Площадь поверхности вращения.
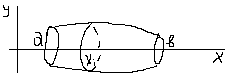
Разобьем 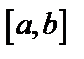 на
на 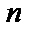 частей и проведем ломаную. При вращении ломаной получаются усеченные конусы (цилиндры). Площадь поверхности
частей и проведем ломаную. При вращении ломаной получаются усеченные конусы (цилиндры). Площадь поверхности 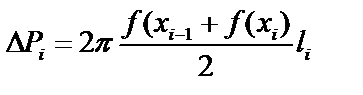 , длина хорды
, длина хорды 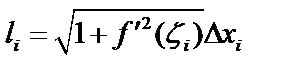 ,
, 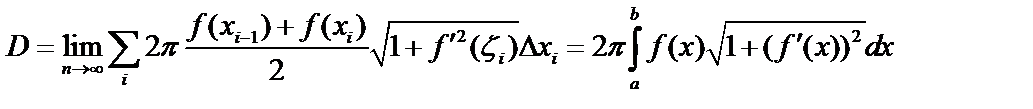 .
.
Пример: Объем тела, образованного вращением вокруг оси ох фигуры, ограниченной линиями: 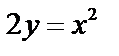 и
и 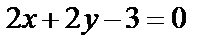 .
.
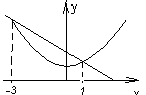
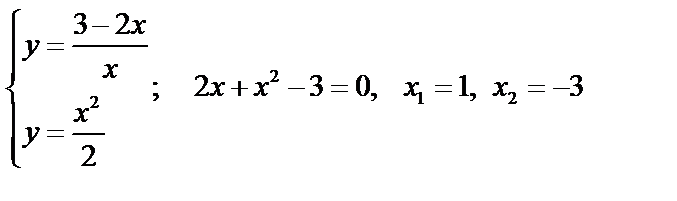 .
.
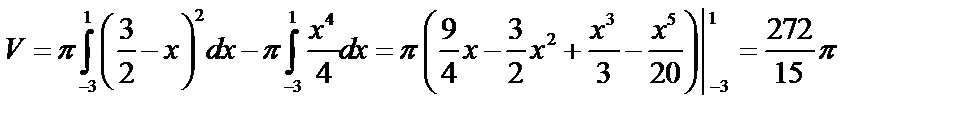 .
.








