Глава 10. Неопределенный интеграл
10.1. Первообразная и неопределенный интеграл. Непосредственное интегрирование
Основная задача дифференциального исчисления – отыскание производной заданной функции. Однако имеется обратная задача: по данной 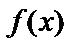 найти
найти 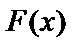 , производная которой равна
, производная которой равна 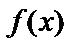 ,
, 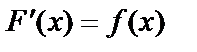 .
.
Лемма: Функция, производная которой на некотором промежутке равна нулю, является константой.
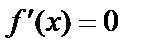 по т. Лагранжа
по т. Лагранжа
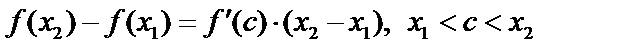 ,
, 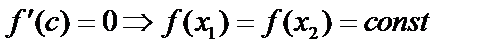 .
.
Теорема. Если 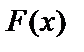 – первообразная для функции
– первообразная для функции 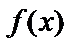 на некотором промежутке X , то любая другая первообразная имеет вид
на некотором промежутке X , то любая другая первообразная имеет вид 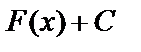 .
.
Определение. Если функция 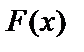 – первообразная для
– первообразная для 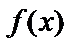 , то множество функций
, то множество функций 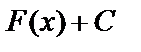 называется неопределенным интегралом от
называется неопределенным интегралом от 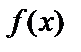 и обозначается:
и обозначается: 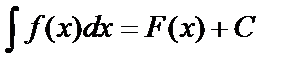 , где
, где 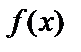 – подынтегральная функция,
– подынтегральная функция, 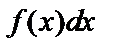 – подынтегральное выражение, x – переменная интегрирования.
– подынтегральное выражение, x – переменная интегрирования.
Восстановление функции по ее производной или отыскание неопределенного интеграла называется интегрированием.
Свойства неопределённого интеграла:
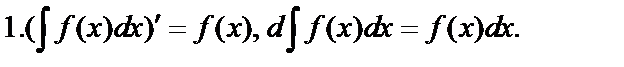
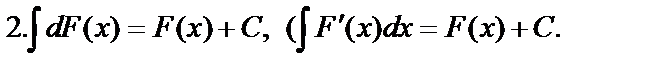
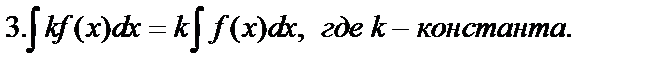
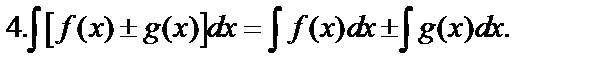
Табличные интегралы:
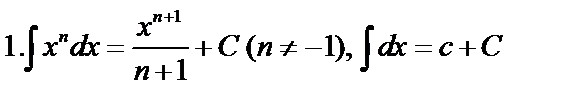
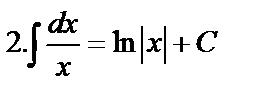
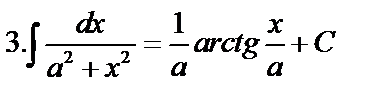
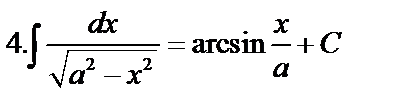
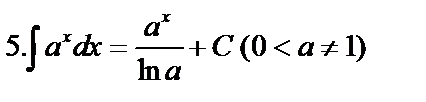
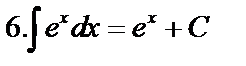
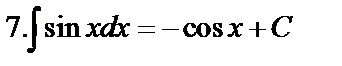
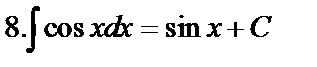
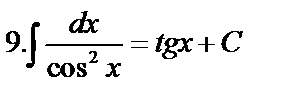
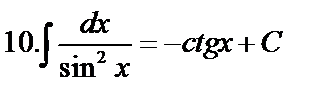
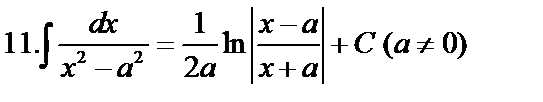
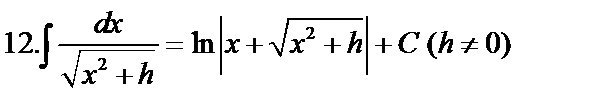
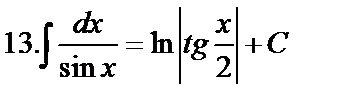
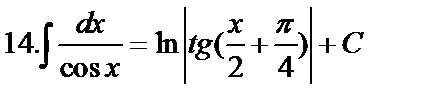
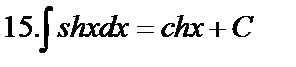
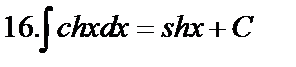
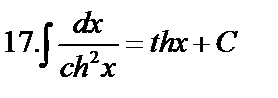
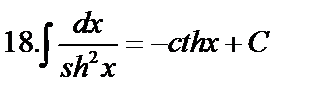
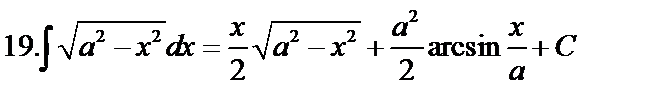
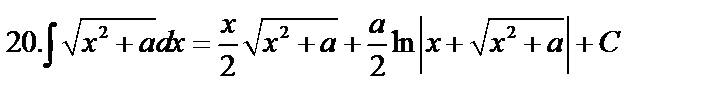
Непосредственное интегрирование
Вычисление интеграла путем использования таблиц и основных свойств называется непосредственным интегрированием.
Примеры.
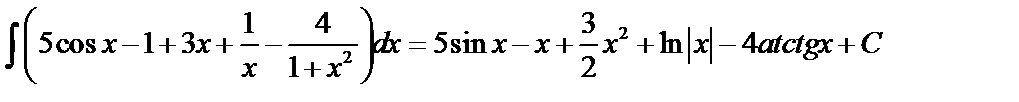 .
.
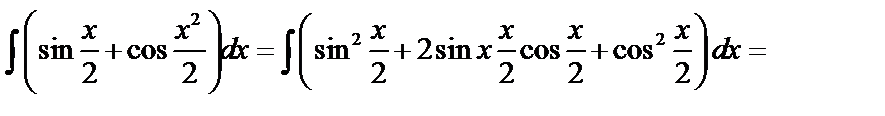
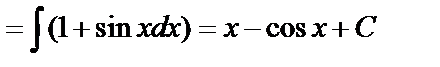 .
.
10.2. Метод подстановки. Интегрирование по частям
Если известно, что 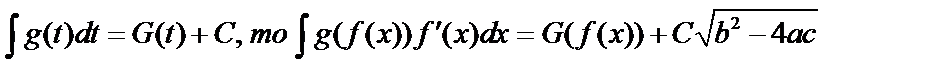 .
.
Это вытекает из правила дифференцирования сложной функции.
Примеры:
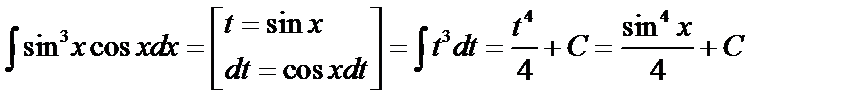 .
.
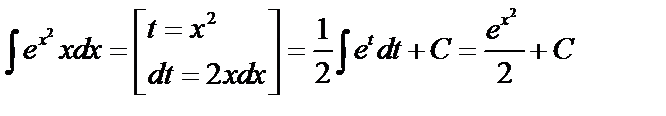 .
.
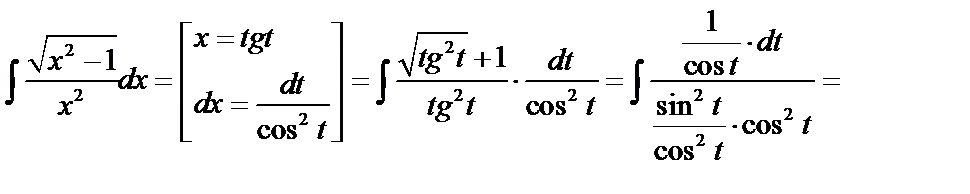
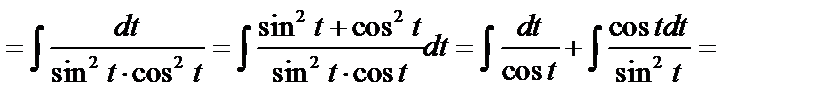
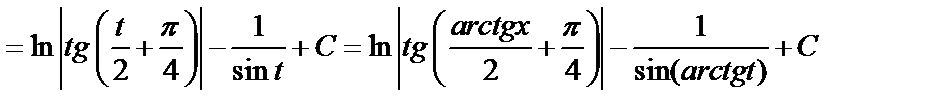 .
.
Интегрирование по частям
Нет формулы, выражающий интеграл от произведения функций через интеграл от сомножителей. Интеграл от элементарной функции не всегда является элементарной функцией.
Пусть имеются дифференцируемые функции 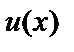 и
и 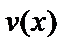 :
: 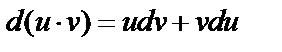 или, интегрируя, получим:
или, интегрируя, получим: 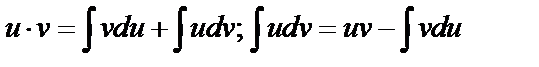 – формула интегрирования по частям.
– формула интегрирования по частям.
При использовании формулы интегрирования по частям необходимо выбрать функцию, тогда оставшаяся часть будет дифференциалом функции 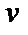 , т.е.
, т.е. 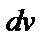 . Можно указать следующие случаи:
. Можно указать следующие случаи:
1. 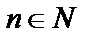
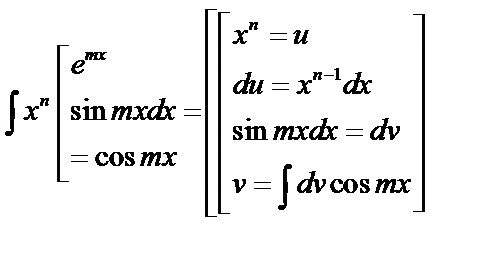 .
.
В этом случае последовательное дифференцирование уменьшает показатель 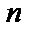 до нуля. Наиболее простой случай, когда
до нуля. Наиболее простой случай, когда 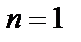 .
.
2. 
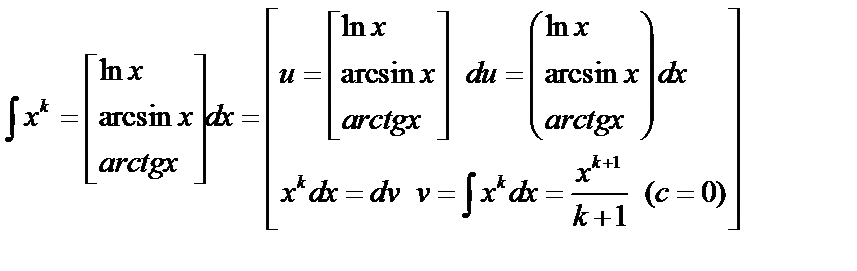
В этом случае дифференцирование указанных функций обычно упрощает нахождение интеграла.
Примеры:
1) 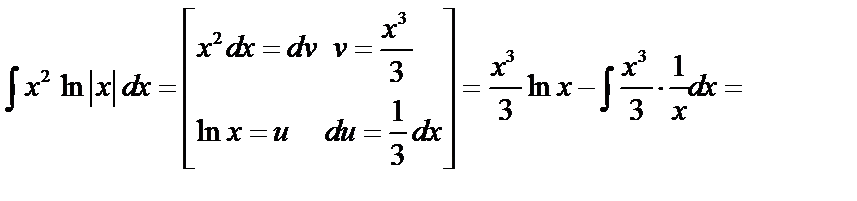
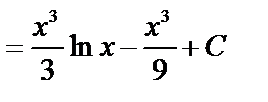
2.) 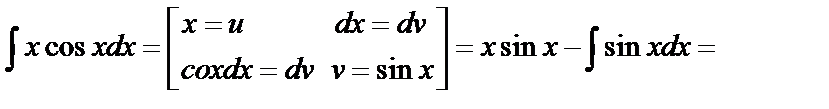
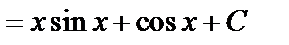
3.) 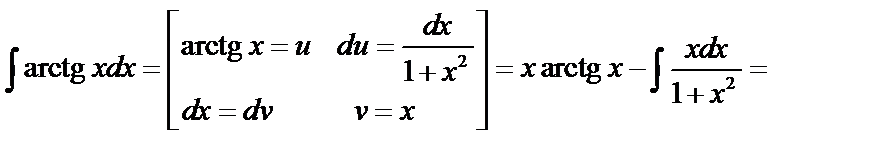
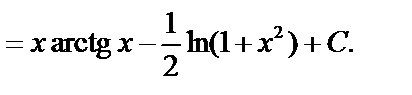
4.) 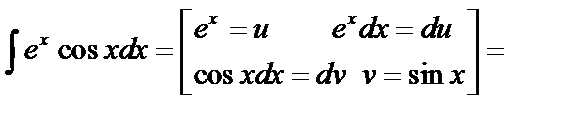
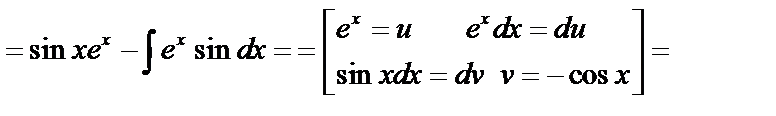
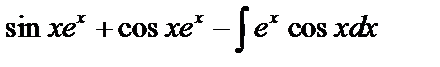 , тогда
, тогда
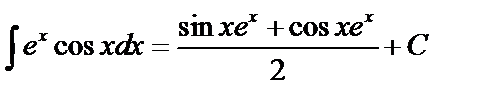 .
.
10.3. Интегрирование рациональных функций. Разложение на простейшие дроби
Рассмотрим рациональную функцию вида 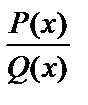 , где
, где 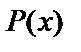 и
и 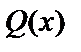 – многочлены. Многочлен – это выражение вида
– многочлены. Многочлен – это выражение вида 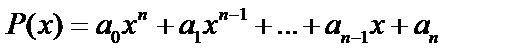 .
.
Если степень многочлена в числителе равна или больше степени многочлена в знаменателе, то дробь называется неправильной и необходимо выполнить деление:

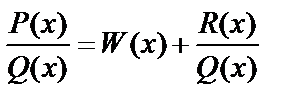 , где
, где 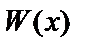 – многочлен.
– многочлен.
Пример
а) 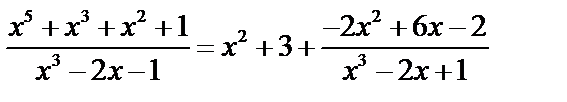 .
.
б) 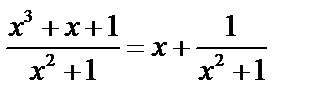 .
.
Далее будем рассматривать правильные дроби (т.е. старшая степень числителя меньше старшей степени знаменателя), т. к. интегрирование функции 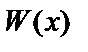 – табличное. Если
– табличное. Если 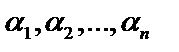 – корни уравнения
– корни уравнения 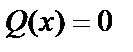 , то многочлен можно представить в виде
, то многочлен можно представить в виде 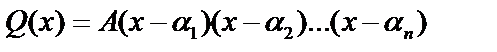 , где
, где 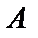 – коэффициент при старшей степени многочлена. Выражения
– коэффициент при старшей степени многочлена. Выражения 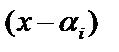 называют линейным множителем.
называют линейным множителем.
Среди корней могут быть и комплексные, в этом случае элементарными множителями будут выражения 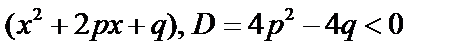 . Кроме того, корни могут быть кратными (одинаковыми). Окончательно имеем:
. Кроме того, корни могут быть кратными (одинаковыми). Окончательно имеем: 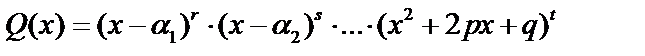 где
где 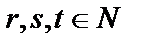 .
.
В высшей алгебре доказывается, что правильную дробь можно представить в виде простейших дробей: 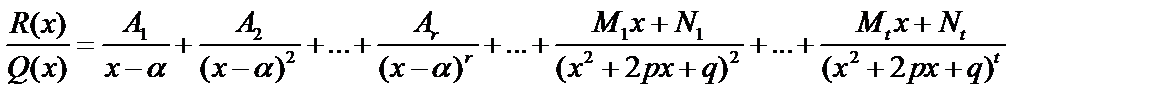 Это разложение рациональной функции на простейшие дроби.
Это разложение рациональной функции на простейшие дроби.
10.4. Интегрирование простейших дробей
Чтобы определить числа 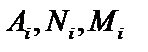 , умножим обе части разложения на
, умножим обе части разложения на  и приравняем коэффициенты при одинаковых степенях x в левой и правой части равенства.
и приравняем коэффициенты при одинаковых степенях x в левой и правой части равенства.
Пример: 
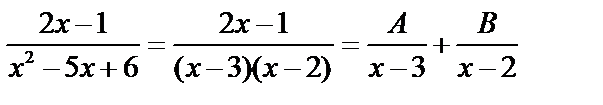 ;
;
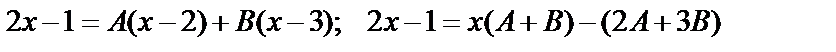
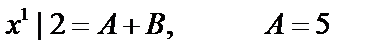
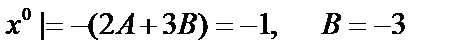
Алгоритм.
1.Выделить правильную дробь.
2.Знаменатель разложить на элементарные множители.
3.Найти коэффициенты в разложении 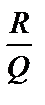 на простейшие дроби.
на простейшие дроби.
После этого задача сводится к нахождению интегралов 4 типов:
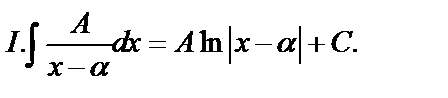
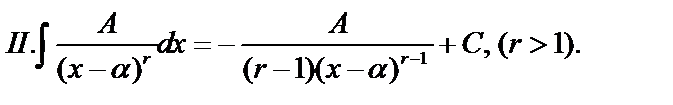
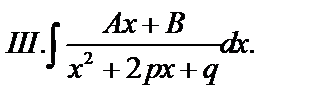
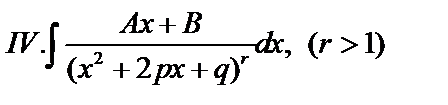 .
. 
Вычислим интеграл типа III.
Выделим в знаменателе полный квадрат:
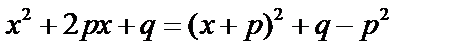 . Используем подстановку,
. Используем подстановку, 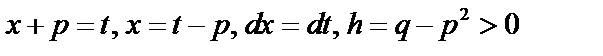 .
.
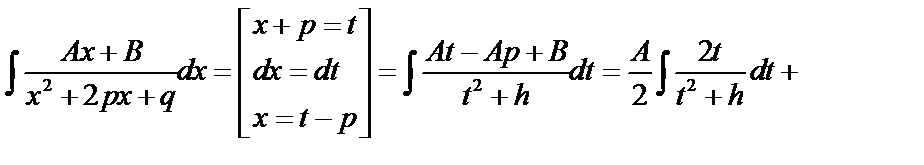
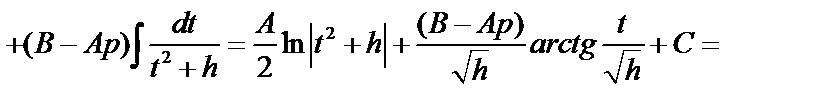
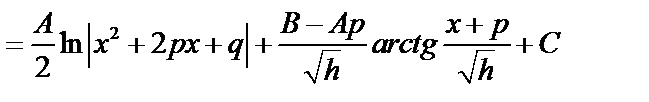 .
.
Пример:
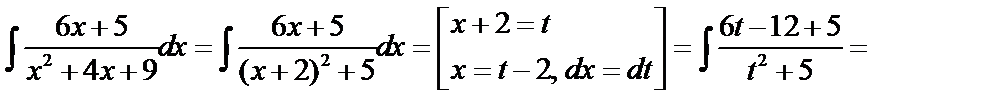
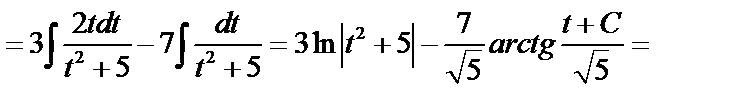
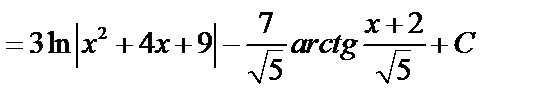 .
.
Вычисление интеграла типа IV.
В числителе записывается производная знаменателя: 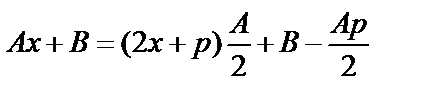 и
и
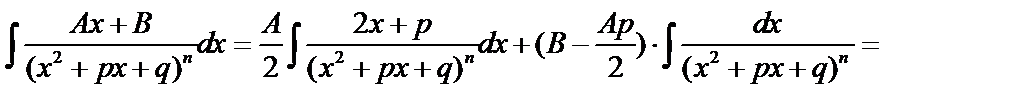
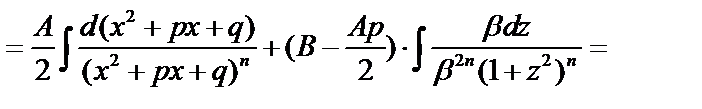
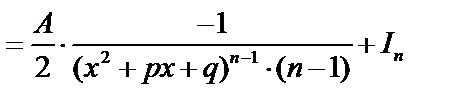 , где
, где 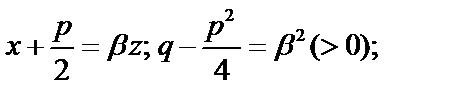
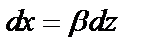 .
.
Интегралы вида 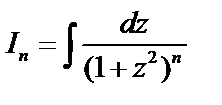 вычисляются по рекуррентной формуле:
вычисляются по рекуррентной формуле:
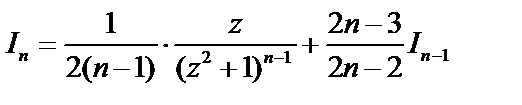 (или формула приведения). Зная, что
(или формула приведения). Зная, что 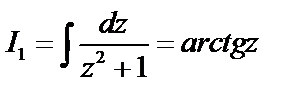 можно вычислить
можно вычислить 
Пример.
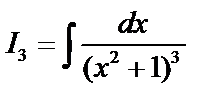 ; по формуле приведения:
; по формуле приведения: 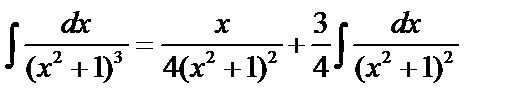
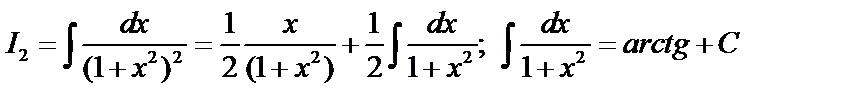 , окончательно,
, окончательно,
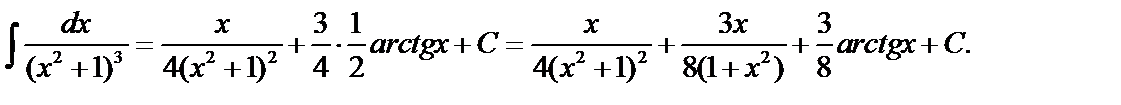
10.5. Интегрирование тригонометрических функций
Интеграл вида 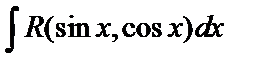 , где
, где 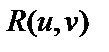 – рациональная функция от
– рациональная функция от 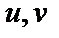 всегда выражается через элементарные функции.
всегда выражается через элементарные функции.
1) Часто используется универсальная подстановка:
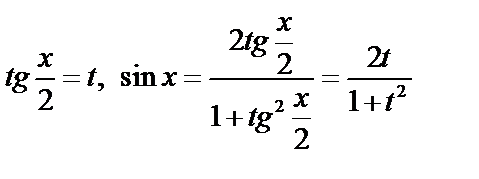 ,
,
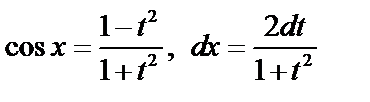
и получается 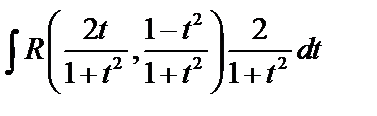 от рациональной функции
от рациональной функции  .
.
Использование этой подстановки обычно связано с громоздкими вычислениями.
2) Если имеет место тождество 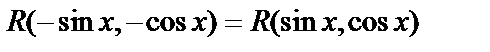 , то можно применить подстановку
, то можно применить подстановку 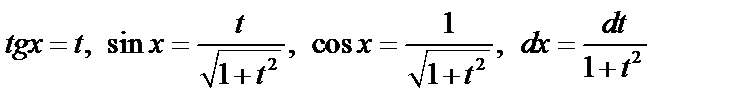 .
.
Пример 1.
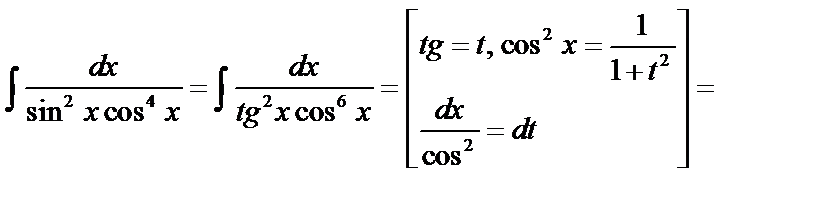
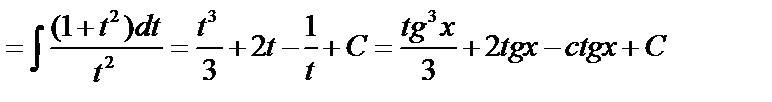
Пример 2.
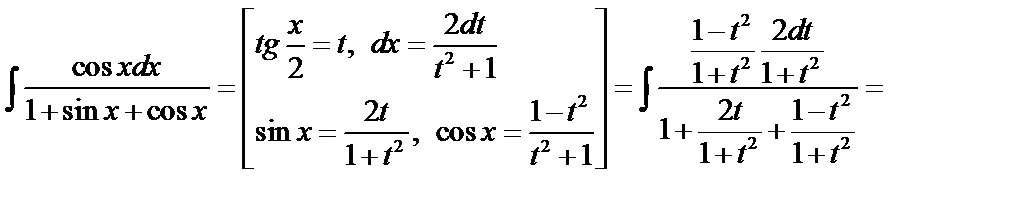


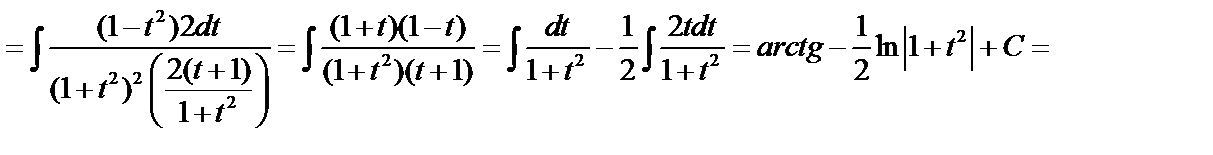
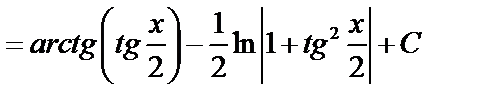 .
.
3) Интегралы вида 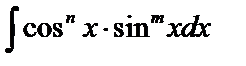 , где m и n – целые числа любого знака.
, где m и n – целые числа любого знака.
а) если 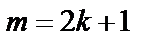 – нечетное, тогда
– нечетное, тогда 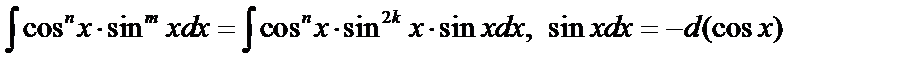 , используется подстановка.
, используется подстановка. 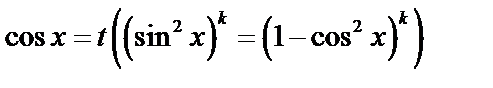 .
.
б) если n – нечетное, тогда 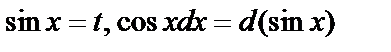 .
.
в) если m и n четные, то можно использовать подстановку 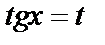 , или понизить степень:
, или понизить степень:
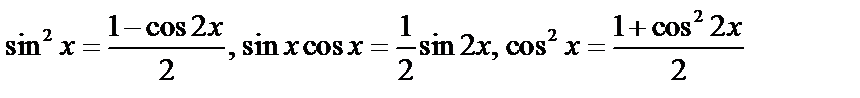 .
.
4) Часто используют формулы:
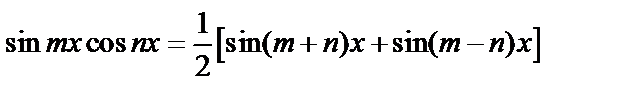 ,
,
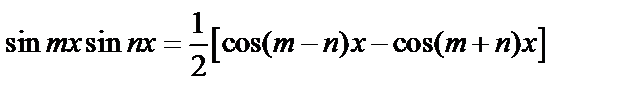 ,
,
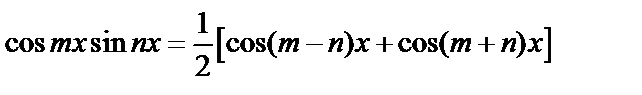 .
.
Пример3. 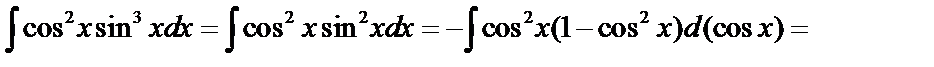
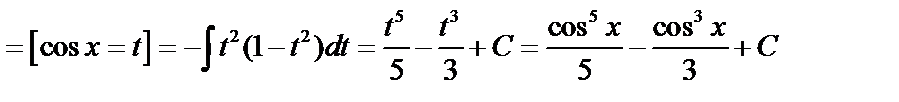 .
.
10.6. Интегрирование некоторых иррациональных функций
I. Рассмотрим интеграл вида 
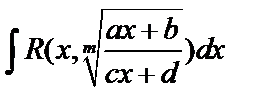 , где
, где 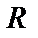 – рациональная функция. Используем подстановку
– рациональная функция. Используем подстановку 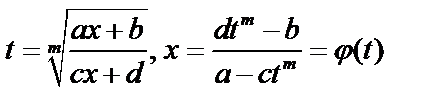 тогда необходимо вычислить
тогда необходимо вычислить 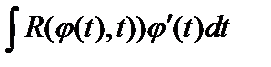 , т.е. интеграл от рациональной функции. Затем возвращаемся к переменной
, т.е. интеграл от рациональной функции. Затем возвращаемся к переменной 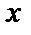 . По этой же методике можно вычислять и
. По этой же методике можно вычислять и 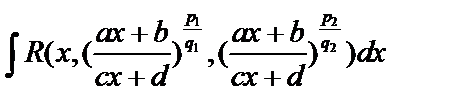 . Необходимо привести к общему знаменателю
. Необходимо привести к общему знаменателю 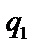 и
и 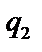 : если он равен
: если он равен 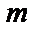 , то положить
, то положить 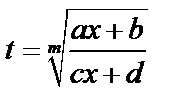 .
.
Пример 1.
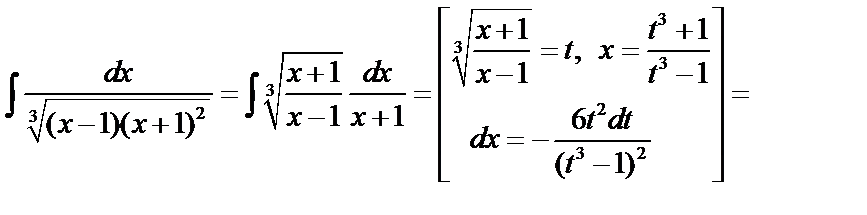
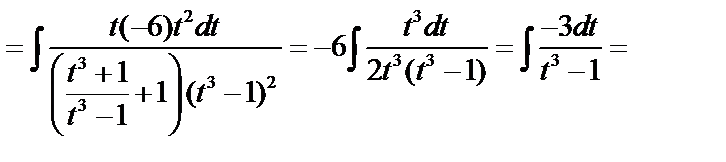
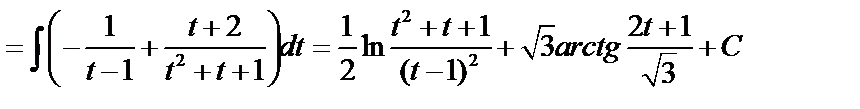 .
.
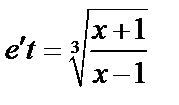 .
.
Пример 2.
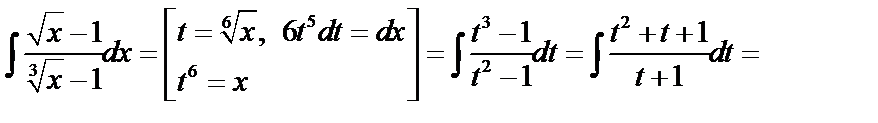
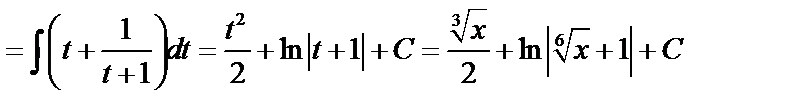 .
.
II. Интегралы вида 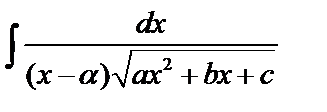 - подстановка
- подстановка 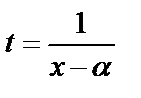 .
.
Пример 3.
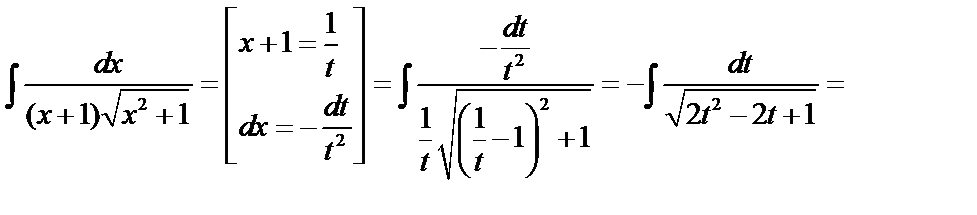
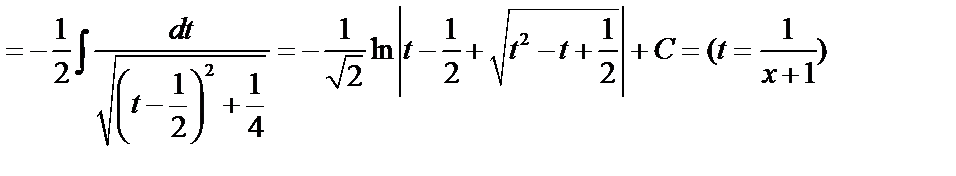 .
.
.
III. Тригонометрические подстановки:
а) Если интеграл содержит радикал 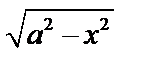 , то подстановка
, то подстановка 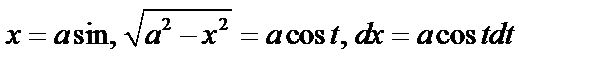 .
.
б) Если интеграл содержит радикал 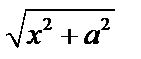 , то подстановка
, то подстановка 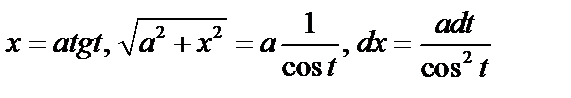 .
.
в) Если интеграл содержит радикал 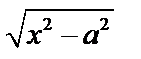 , то
, то 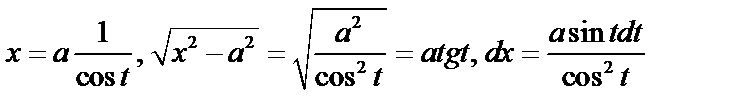
IV. 
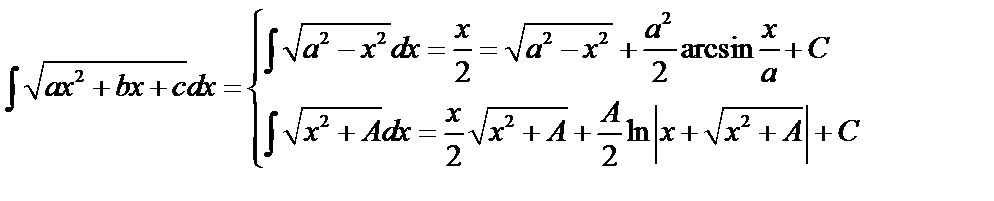 .
.
Например: 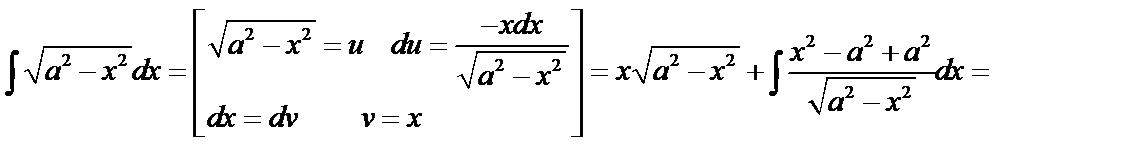
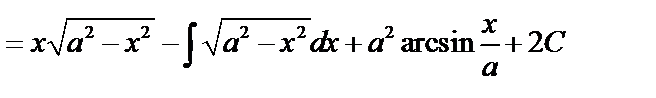 .
.
тогда
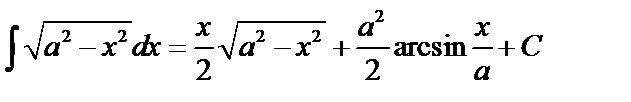 . Аналогично для второго интеграла.
. Аналогично для второго интеграла.








