Глава 8. Основные теоремы дифференциального исчисления
8.1. Теорема Ферма
Пусть 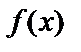 определена на интервале
определена на интервале 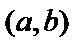 и в точке
и в точке 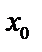 интервала достигает наибольшего (наименьшего) значения. Тогда, если в
интервала достигает наибольшего (наименьшего) значения. Тогда, если в 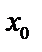 существует производная, то она равна 0, т.е.
существует производная, то она равна 0, т.е. 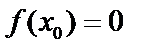 .
.
8.2. Теорема Ролля
Если 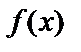 определена и непрерывна на отрезке
определена и непрерывна на отрезке 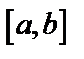 , дифференцируема на
, дифференцируема на 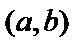 и на концах принимает одинаковое значение
и на концах принимает одинаковое значение 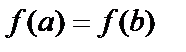 ,то существует
,то существует 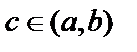 , в которой
, в которой 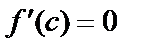 .
.
8.3. Теорема Лагранжа
Пусть 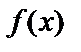 определена и непрерывна на отрезке
определена и непрерывна на отрезке 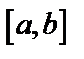 , дифференцируемая на
, дифференцируемая на 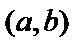 . Тогда существует
. Тогда существует 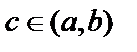 , такая, что
, такая, что 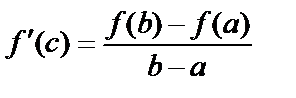 .
.
8.4. Теорема Коши
Пусть 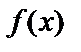 и
и 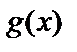 непрерывна на
непрерывна на 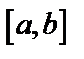 и дифференцируема на
и дифференцируема на 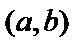 , причем
, причем 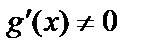 . Тогда существует
. Тогда существует 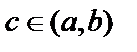 ,такая, что
,такая, что 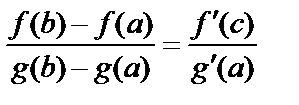 .
.
8.5. Правило Лопиталя
 Теорема (правило) Лопиталя . Пусть функции
Теорема (правило) Лопиталя . Пусть функции 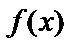 и
и 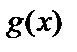 определены и дифференцируемы на промежутке
определены и дифференцируемы на промежутке 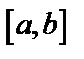 ,
, 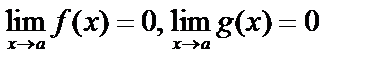 ,
, 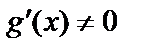 и существует предел
и существует предел 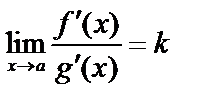 . Тогда и
. Тогда и 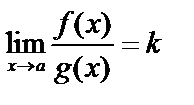 .
.
Глава 9. Приложения производной
9.1. Интервалы монотонности. Признаки экстремума
Множество точек 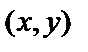 координатной плоскости ХОУ, координаты которых связаны уравнением
координатной плоскости ХОУ, координаты которых связаны уравнением 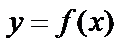 , называется графиком данной функции.
, называется графиком данной функции.
По производной функции можно судить о возрастании (убывании) самой функции. Напомним, что 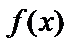 называется возрастающей в некотором интервале, если для любых
называется возрастающей в некотором интервале, если для любых 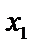 и
и 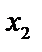 из этого интервала из неравенства
из этого интервала из неравенства 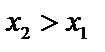 следует неравенство
следует неравенство
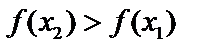 Убывающей:
Убывающей: 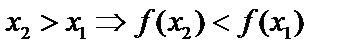 .
.
Теорема. Пусть 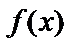 определена на отрезке
определена на отрезке 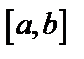 и имеет непрерывную производную
и имеет непрерывную производную 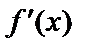 внутри отрезка. Чтобы
внутри отрезка. Чтобы 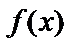 была возрастающей (убывающей), достаточно
была возрастающей (убывающей), достаточно 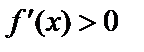 ,
, 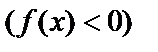 .
.
Рассмотрим возрастание. Возьмем два значения 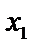 и
и 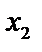
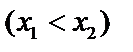 из
из 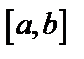 и применим формулу Лагранжа:
и применим формулу Лагранжа: 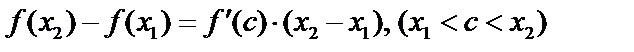 . Так как
. Так как 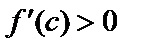 , и
, и 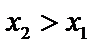 , то
, то 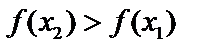 – возрастающая. Аналогично – убывающая.
– возрастающая. Аналогично – убывающая.
Геометрический смысл – производная – угловой коэффициент касательной. Значение коэффициента показывает, наклонена ли касательная вверх или вниз.
Экстремумы функции
Функция 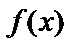 имеет в т.
имеет в т. 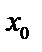 максимум, если
максимум, если 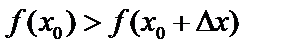 , где
, где 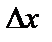 – достаточно малая по величине. Функция
– достаточно малая по величине. Функция 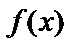 имеет в т.
имеет в т. 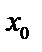 минимум, если
минимум, если 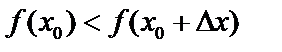 .
.
Если в т. 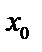
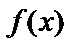 имеет max или min, то говорят, что в этой точке имеет место экстремум.
имеет max или min, то говорят, что в этой точке имеет место экстремум.
Необходимое условие экстремума. Если существует конечная производная, то по теореме Ферма 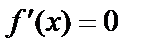 .
.
Экстремумы необходимо искать в тех точках, где 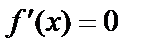 или не существует. Такие точки называются стационарными (критическими).
или не существует. Такие точки называются стационарными (критическими).
Если допустить, что в отдельных точках нет конечной производной, то следует отнести к критическим и эти точки. Критические точки следует проверить, в них необязательно экстремум ( 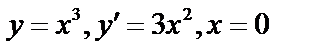 , нет экстремума).
, нет экстремума).
Первый достаточный признак экстремума.
Пусть т. 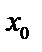 является критической для
является критической для 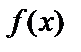 , а
, а 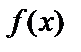 непрерывна и дифференцируема во всех точках некоторого интервала, содержащего эту точку (за исключением, возможно, самой точки
непрерывна и дифференцируема во всех точках некоторого интервала, содержащего эту точку (за исключением, возможно, самой точки 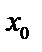 ). Тогда возможно:
). Тогда возможно:
1) 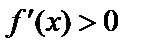 при
при 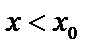 и
и 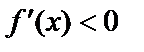 при
при 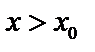 , то есть производная при переходе через т.
, то есть производная при переходе через т. 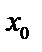 меняет знак с «+» на «–». Тогда при
меняет знак с «+» на «–». Тогда при 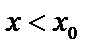
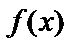 возрастает, а при
возрастает, а при 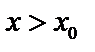 (в данном интервале) убывает, значит, значение
(в данном интервале) убывает, значит, значение 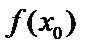 будет наибольшим – в т.
будет наибольшим – в т. 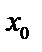
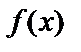 имеет max.
имеет max.
2) 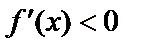 при
при 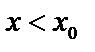 ,
, 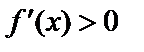 при
при 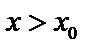 , то есть с «–» на «+» – min.
, то есть с «–» на «+» – min.
3) 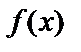 не меняет знак при переходе через
не меняет знак при переходе через 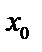 . Тогда
. Тогда 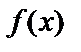 либо возрастает, либо убывает, экстремума нет.
либо возрастает, либо убывает, экстремума нет.
Второй достаточный признак экстремума.
Пусть 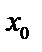 – критическая точка и
– критическая точка и 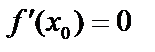 ,
, 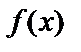 имеет вторую производную в интервале и в самой т.
имеет вторую производную в интервале и в самой т. 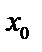 . Тогда, если
. Тогда, если 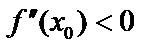 – max ,
– max , 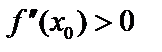 – min.
– min.
По определению производной: 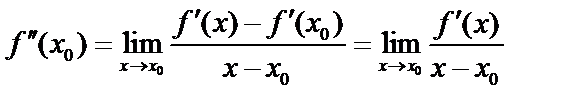 . Если
. Если 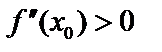 , то дробь > 0. При
, то дробь > 0. При 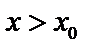 знаменатель <0,
знаменатель <0, 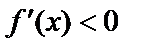 (убывает) и при
(убывает) и при 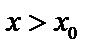 знаменатель >0 (возрастает) – min по первому признаку. Аналогично – max, если
знаменатель >0 (возрастает) – min по первому признаку. Аналогично – max, если 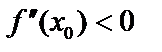 .
.
Исследования по второму признаку производят редко.
Наибольшее и наименьшее значения функции на отрезке.
Если 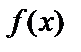 непрерывна на отрезке
непрерывна на отрезке 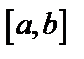 , то на этом отрезке всегда имеются точки, в которых она принимает max и min значения. Этих значений
, то на этом отрезке всегда имеются точки, в которых она принимает max и min значения. Этих значений 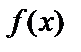 достигает или в критических точках или на концах отрезка.
достигает или в критических точках или на концах отрезка.
Правило. Чтобы определить наибольшее и наименьшее значения 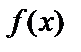 на отрезке, надо:
на отрезке, надо:
1. Определить критические точки, принадлежащие 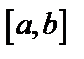 ;
;
2. Вычислить значение функции в этих критических точках и на концах отрезка;
3. Выбрать наибольшее и наименьшее значения из полученных чисел.
9.2. Выпуклость и вогнутость. Точки перегиба
Кривая обращена выпуклостью вниз, если на интервале 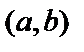 она лежит выше касательной, проведенной в любой точке (вверх, если ниже касательной).
она лежит выше касательной, проведенной в любой точке (вверх, если ниже касательной).
Дуги кривой, называют выпуклыми на интервале 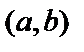 , если они лежат ниже касательной, проведенной в любой точке
, если они лежат ниже касательной, проведенной в любой точке 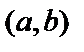 . Дуги кривой называют вогнутыми на
. Дуги кривой называют вогнутыми на 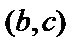 , если они лежат выше касательных.
, если они лежат выше касательных.
Правило. Интервалы, в которых кривая выпуклая, определяются из неравенства 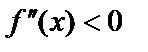 , а интервалы, в которых вогнутая из неравенства
, а интервалы, в которых вогнутая из неравенства 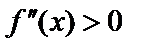 .
.
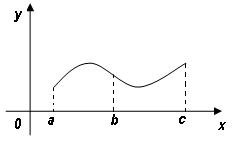
Точка перегиба – точка, отделяющая ее выпуклую дугу от вогнутой. Точки перегиба следует искать среди точек, в которых 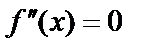 ,
, 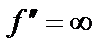 или
или 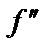 не существует.
не существует.
При 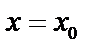 перегиб будет в том случае, когда при переходе через эту точку
перегиб будет в том случае, когда при переходе через эту точку 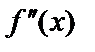 меняет знак.
меняет знак.
9.3. Асимптоты графика функции
Прямая l называется асимптотой кривой, если расстояние d от переменной точки M кривой до этой прямой при удалении т. М в бесконечность (от начала координат) стремится к нулю.
Различают вертикальные и наклонные асимптоты.
1. Вертикальная: кривая имеет вертикальную асимптоту 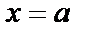 , если
, если 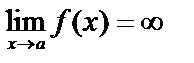 . Необходимо отыскать те значения аргумента, при которых
. Необходимо отыскать те значения аргумента, при которых 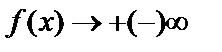 .
.
2. Наклонные: ищем асимптоту в виде 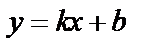 . Найдем k и b .
. Найдем k и b .
Очевидно, что 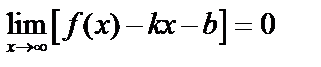 , или
, или 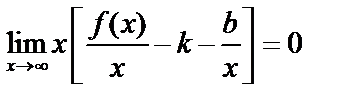 , так как
, так как 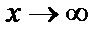 , то
, то 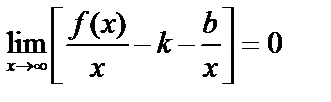 , но
, но 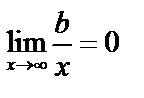 , тогда
, тогда 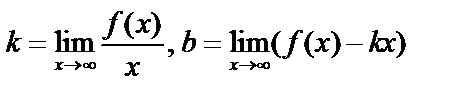 . Необходимо рассматривать случай
. Необходимо рассматривать случай 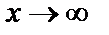 (и Лопиталь). Если предел не существует, то асимптот нет. Иногда существует две асимптоты:
(и Лопиталь). Если предел не существует, то асимптот нет. Иногда существует две асимптоты: 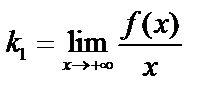 и
и 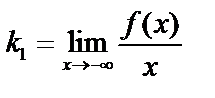 и аналогично
и аналогично 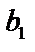 и
и 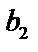 .
.
Общий план исследования функции и построения графика.
1) Определение области существования функции.
2) Четность, нечетность функции.
3) Точки пересечения с осями, интервалы знакопостоянства.
4) Асимптоты.
5) Интервалы возрастания и убывания.
6) Экстремумы.
7) Интервалы выпуклости и вогнутости.
8) Точки перегиба.








