Производная неявной и параметрической функции
Логарифмическая производная
Производная степенно-показательной функции
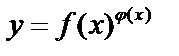. Найдем 
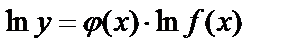. Дифференцируя, получим
.
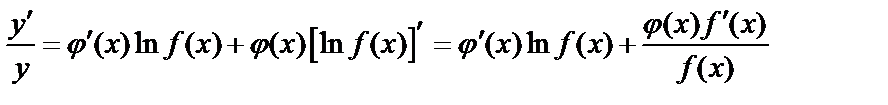Учитывая, что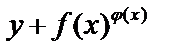 
, получим после преобразований
.
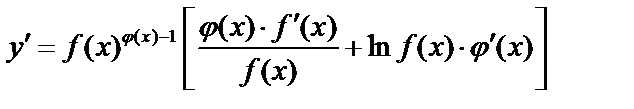Замечание. Производная логарифмической функции
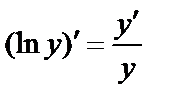называется логарифмической производной. Ее удобно использовать для нахождения производных функций, выражения которых существенно упрощаются при логарифмировании.
Пример 1. Вычислить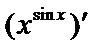 
.
.
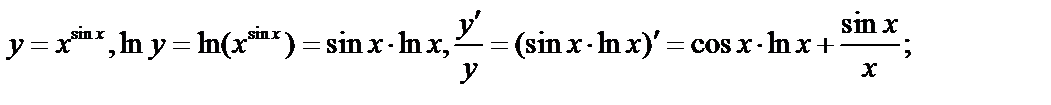
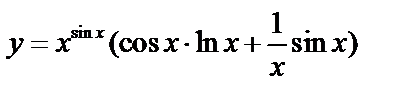Пример 2.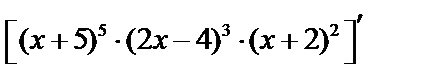 
.
Логарифмируем:
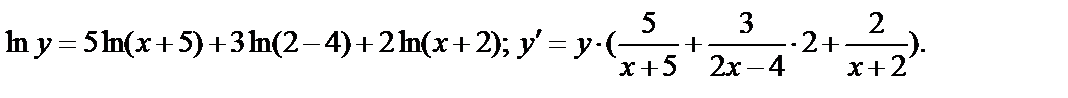Производная неявной функции.
Если задана неявная функция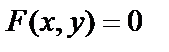 
, то для вычисления производной надо взять производные от правой и левой частей, помня, что 
.
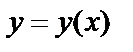Например,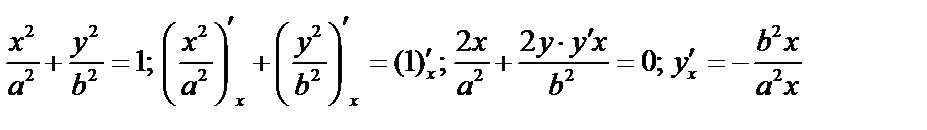 
.
.
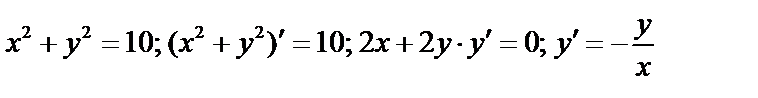Параметрическое задание функции
Пусть даны два уравнения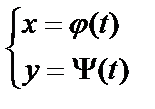 
.
Каждому значению t соответствует x и y на плоскости. Если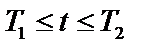 
, то эта точка описывает кривую на плоскости – кривая задана параметрически, 
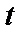– параметр. 
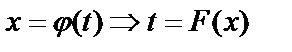, то 
.
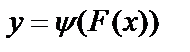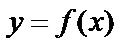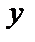Такое задание определяет 
, 
от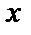 
задается параметрически. Используется в механике.
Производная. Ищем производную сложной функции:
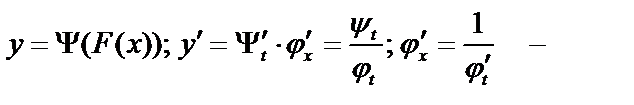производная обратной функции.
Пример.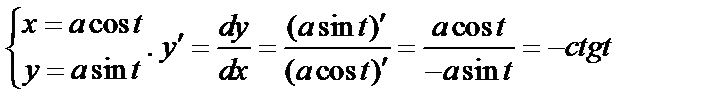 
.
7.8. Дифференциал функции
Пусть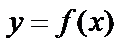 
и аргумент 
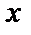получил приращение 
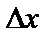. Тогда дифференциалом называется величина 
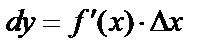, но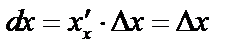 
, поэтому 
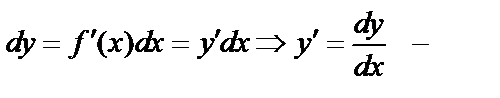отношение дифференциалов.
Вычисление дифференциала функции называется ее дифференцированием, при этом вычисляется производная, поэтому процесс вычисления производной часто называется дифференцированием.
Дифференциал – главная линейная часть приращения функции.
Функция, обладающая дифференциалом, называется дифференцируемой.
У дифференцируемой функции производная должна быть конечной.
Свойства дифференциала
1. 
;
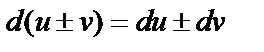2. 
;
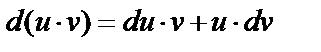3. 
.
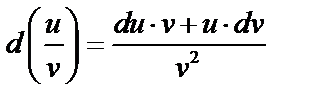Найдем выражение для дифференциала сложной функции: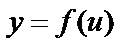 
, где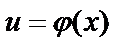 
. По правилу дифференцирования сложной функции: 
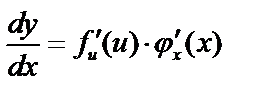, то есть 
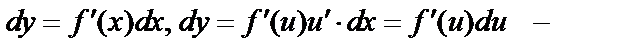инвариантность дифференциала – дифференциал сложной функции имеет такой же вид, как и для простой переменной.
Дифференциал широко применяется в приближенных вычислениях.
Дифференциал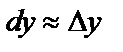 
, если 
.
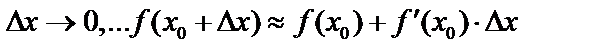7.9. Производные и дифференциалы высших порядков
Если вычислить производную от первой производной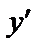 
, то получим вторую производную: 
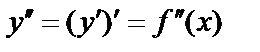. Производная от второй производной: 
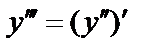– третья производная. Производная n-го порядка – производная от производной 
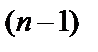порядка: 
.
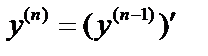Пример: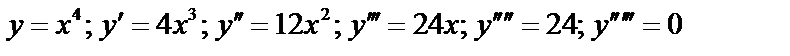 
;
.
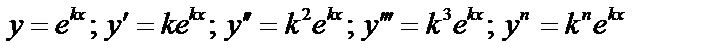Для дифференцируемых функци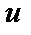й 
и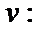 
;
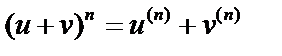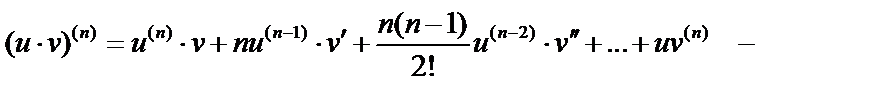формула Лейбница.
Дифференциалы высших порядков.
Дифференциал второго порядка:
,
.
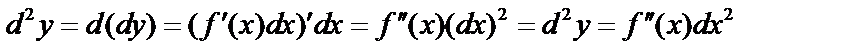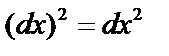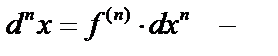дифференциал n-го порядка.