Глава 6. Пределы и непрерывность
6.1. Предел числовой последовательности
Если по некоторому закону каждому натуральному числу n поставлено в соответствие вполне определенное число 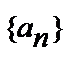 , то говорят, что задана числовая последовательность
, то говорят, что задана числовая последовательность 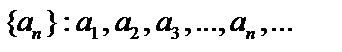 . Числа
. Числа 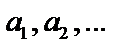 – члены последовательности,
– члены последовательности, 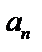 – n-й член последовательности.
– n-й член последовательности.
Число А называется пределом числовой последовательности 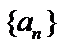 , если для любого сколь угодно малого числа
, если для любого сколь угодно малого числа 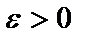 найдётся такой номер N, что для всех членов последовательности с
найдётся такой номер N, что для всех членов последовательности с 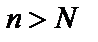 будет выполняться неравенство
будет выполняться неравенство 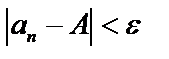 или
или 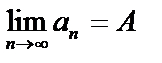 .
.
Пусть 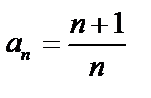 , тогда
, тогда 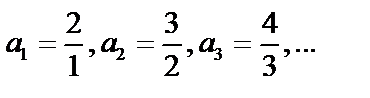 .
. 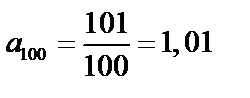
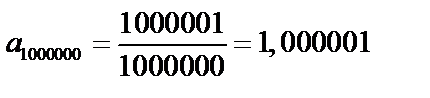 и т.д. С ростом n члены последовательности стремятся к 1, и величина разности
и т.д. С ростом n члены последовательности стремятся к 1, и величина разности 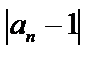 становится все меньше. Тогда
становится все меньше. Тогда 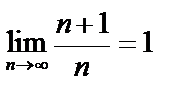 .
.
6.2. Предел функции в бесконечности и в точке
Предел функции в бесконечности
Число А называется пределом функции 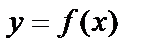 при х, стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа
при х, стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа 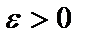 , найдется такое положительное число
, найдется такое положительное число 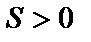 , что для всех х таких, что
, что для всех х таких, что 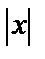 >S, верно неравенство:
>S, верно неравенство: 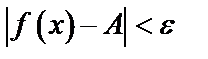 и обозначается
и обозначается 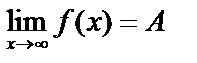 .
.
Рассмотрим предел функции в точке. Число А называется пределом функции 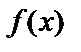 при
при 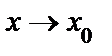 , если для любого, даже сколь угодно малого положительного числа
, если для любого, даже сколь угодно малого положительного числа 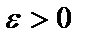 , найдется такое положительное число
, найдется такое положительное число 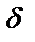 >0 , что для всех
>0 , что для всех 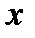 , не равных
, не равных 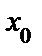 и удовлетворяющих неравенству
и удовлетворяющих неравенству 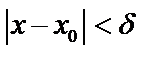 выполняется неравенство
выполняется неравенство 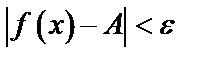 и обозначается
и обозначается 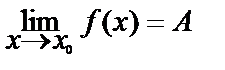 . Если
. Если 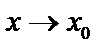 и
и 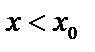 , то это предел слева
, то это предел слева 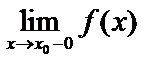 ; если
; если 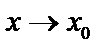 и
и 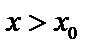 , то это предел справа
, то это предел справа 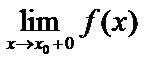 .
.
6.3. Бесконечно малые величины
Функция 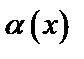 называется бесконечно малой величиной при
называется бесконечно малой величиной при 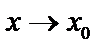 , если её предел равен 0, т.е.
, если её предел равен 0, т.е. 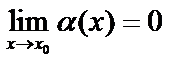 . Например,
. Например, 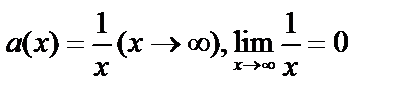 ;
; 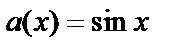 , если
, если 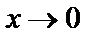 :
: 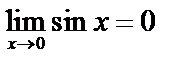 .
.
Теорема. Если 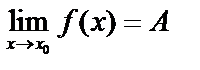 , то
, то 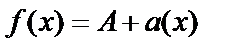 где
где 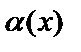 – бесконечно малая при
– бесконечно малая при 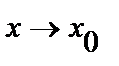 .
.
По условию 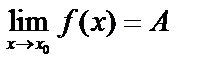 . Это значит, что для любого,
. Это значит, что для любого, 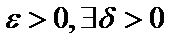 что для всех
что для всех 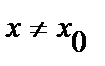 и удовлетворяющих
и удовлетворяющих 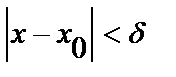 верно
верно 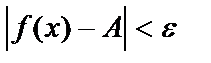 . Обозначив
. Обозначив 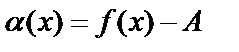 , получим
, получим 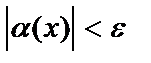 . Это означает, что
. Это означает, что 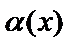 – бесконечно малая при
– бесконечно малая при 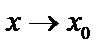 .
.
Обратная теорема. Если 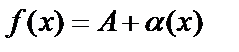 (бесконечно малой), то
(бесконечно малой), то 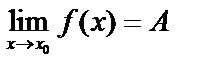 .
.
По условию 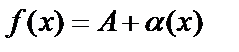 . Т.к.
. Т.к. 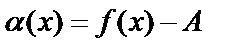 - бесконечно малая при
- бесконечно малая при 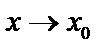 , то
, то 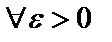
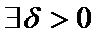 , что для всех
, что для всех 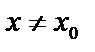 и удовлетворяющих
и удовлетворяющих 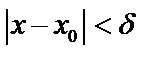 верно
верно 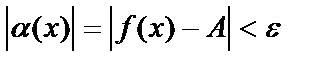 .
.
это означает, что 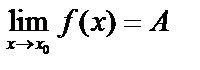 .
.
Свойства бесконечно малых величин:
1. Сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
2. Произведение бесконечно малой величины на константу есть величина бесконечно малая.
3. Частное от деления бесконечно малой величины на функцию, предел которой отличен от 0, есть величина бесконечно малая.
Замечание. Пусть 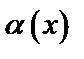 и
и 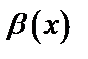 две бесконечно малые величины. В этом случае их отношение
две бесконечно малые величины. В этом случае их отношение 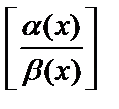 называется неопределенностью
называется неопределенностью 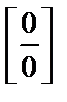 и требует дальнейших вычислений.
и требует дальнейших вычислений.
Сравнение бесконечных малых.
Пусть имеется несколько бесконечно малых величин 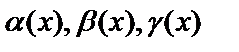
1. Если 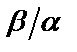 имеет конечный и не равный нулю предел, т.е.
имеет конечный и не равный нулю предел, т.е. 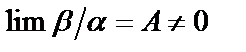 и
и 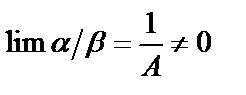 , то бесконечно малые
, то бесконечно малые 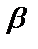 и
и 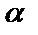 называются бесконечно малыми одного порядка малости.
называются бесконечно малыми одного порядка малости.
Пример. 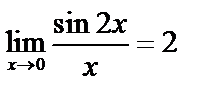 , x и
, x и 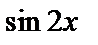 – бесконечно малые одного порядка.
– бесконечно малые одного порядка.
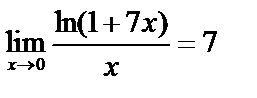 .
.
2. Если 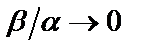 , то есть
, то есть 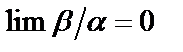 (а
(а 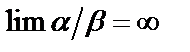 ), то
), то 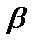 называют бесконечно малой величиной высшего порядка малости, чем бесконечно малая
называют бесконечно малой величиной высшего порядка малости, чем бесконечно малая 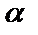 ,
, 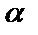 – бесконечно малая низшего порядка, чем
– бесконечно малая низшего порядка, чем 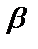 . Запись
. Запись 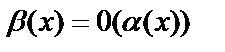 –
– 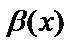 есть 0 малое от
есть 0 малое от 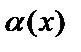 .
.
Пример. 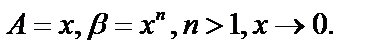
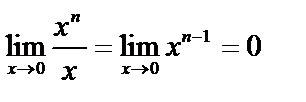 ,
, 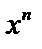 – бесконечно малая величина высшего порядка, чем
– бесконечно малая величина высшего порядка, чем 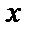 .
.
3. Если 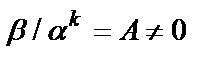 , то
, то 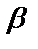 – бесконечно малая
– бесконечно малая 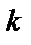 -го порядка относительно бесконечно малой
-го порядка относительно бесконечно малой 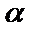 .
.
Пример. 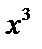 есть бесконечно малая 3 порядка относительно
есть бесконечно малая 3 порядка относительно 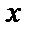 , т.к.
, т.к.
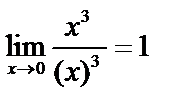 .
.
4. Если 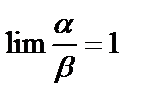 , то α и β называются эквивалентными (равносильными) бесконечно малыми.
, то α и β называются эквивалентными (равносильными) бесконечно малыми.
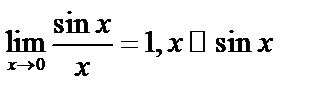 при
при 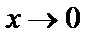
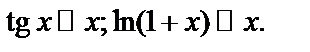
Предел отношения двух бесконечно малых не изменится, если члены отношения заменить равносильными им величинами.
Пример. 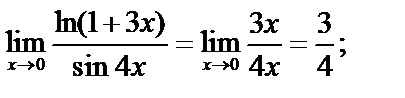
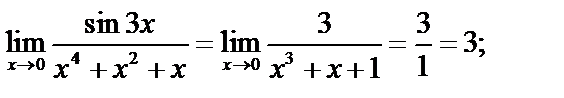
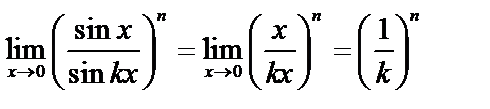
6.4. Бесконечно большие величины
Функция 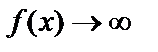 при
при 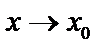 , то есть является бесконечно большой величиной при
, то есть является бесконечно большой величиной при 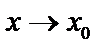 , если для каждого
, если для каждого 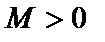 , как бы велико оно не было, можно найти такое
, как бы велико оно не было, можно найти такое 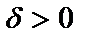 , что для всех
, что для всех 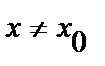 , удовлетворяющих неравенству
, удовлетворяющих неравенству 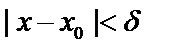 имеет место
имеет место 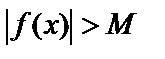 . Запись:
. Запись: 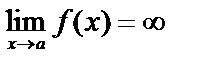 .
.
Свойства:
1. Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.
2. Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.
3. Частное от деления бесконечно большой величины на функцию, имеющую предел, есть величина бесконечно большая.
Замечание 1. Если 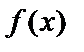 и
и 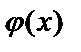 – бесконечно большие величины при
– бесконечно большие величины при 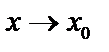 , то
, то 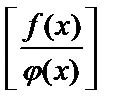 – неопределенность
– неопределенность 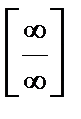 .
. 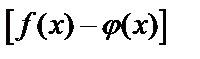 – неопределенность
– неопределенность 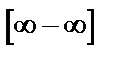 .
.
Теорема. Если 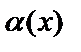 – бесконечно малая при
– бесконечно малая при 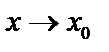 , то величина
, то величина 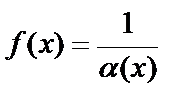 – бесконечно большая при
– бесконечно большая при 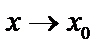 и наоборот.
и наоборот.
6.5. Основные теоремы о пределах
1. Предел алгебраической суммы конечного числа переменных равен алгебраической сумме пределов этих переменных.
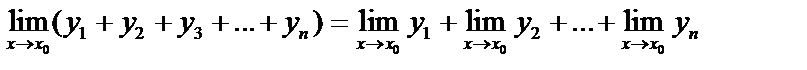 .
.
2. Предел произведения конечного числа переменных равен произведению пределов этих переменных.
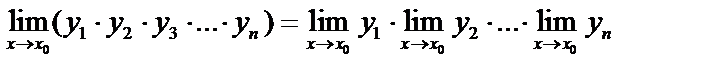 .
.
Следствие.
Постоянный множитель можно выносить за знак предела.
3. Предел частного двух переменных равен частному пределов этих переменных, если предел делителя отличен от нуля, 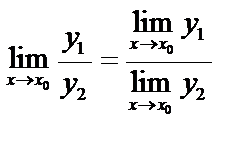 , если
, если 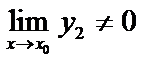 .
.
4. Если 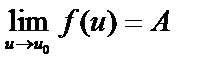 ,
, 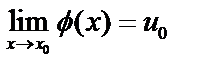 , то предел сложной функции
, то предел сложной функции 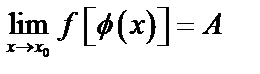 .
.
5. Если в некоторой окрестности точки 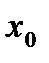 (или при достаточно больших
(или при достаточно больших 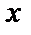 )
) 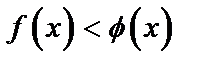 , то
, то 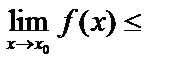
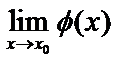 .
.
6. Если в некоторой окрестности точки 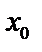 (или при достаточно больших
(или при достаточно больших 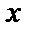 ) функция
) функция 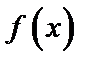 заключена между двумя функциями
заключена между двумя функциями 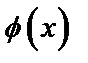 и
и 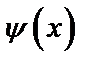 , имеющими одинаковый предел А при
, имеющими одинаковый предел А при 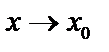 ,то функция имеет
,то функция имеет 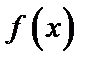 тот же предел.
тот же предел.
Во всех этих теоремах предполагается существование пределов этих функций.
6.7. Первый замечательный предел
Первый замечательный предел: 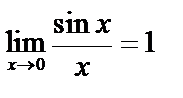 .
.
6.8. Второй замечательный предел
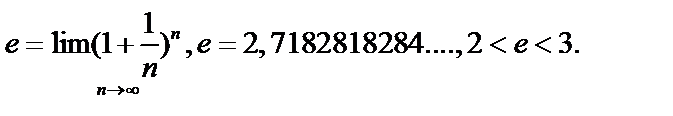
В общем виде: 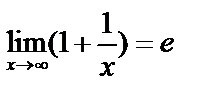 , или
, или 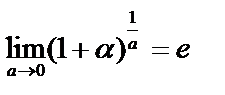 .
.
6.9. Непрерывность функции в точке и на промежутке
Функция называется непрерывной в точке x0, если она удовлетворяет следующим условиям:
1. Функция определена в точке 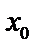 .
.
2. Функция имеет конечный предел при 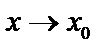 и этот предел равен значению функции в точке
и этот предел равен значению функции в точке 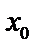 , т.е.
, т.е. 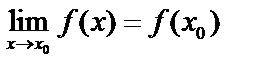 .
.
Функция f(x) называется непрерывной в точке x0, если при ∆х→0 и ∆у→0, то есть бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: 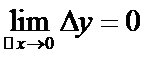 .
.
В противном случае х0 – точка разрыва.
Функция, непрерывная в каждой точке некоторого интервала, называется непрерывной в этом интервале.
Свойства непрерывной функции
1. Если функция 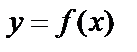 непрерывна на отрезке
непрерывна на отрезке 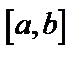 , то она ограничена на этом отрезке и достигает на этом отрезке наибольшего значения М и наименьшего значения m.
, то она ограничена на этом отрезке и достигает на этом отрезке наибольшего значения М и наименьшего значения m.
2. Если f ( x ) непрерывна на отрезке [a,b] и на концах принимают значение разных знаков, то имеется a < c < b, для которой f(c)=0.
6.10.Классификация точек разрыва
Точка х называется точкой разрыва функции f(x), если f(x) в точке х0 не является непрерывной.
Точки разрыва можно разделить на два типа:
1. Разрыв 1 рода. Если функция f(x) имеет в точке х0 конечные пределы слева и справа , не равные между собой, то в точке 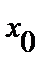 будет разрыв первого рода, т.е.
будет разрыв первого рода, т.е. 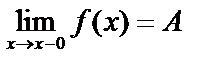 ,
, 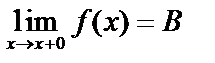 , но
, но 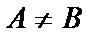 .
.
2. Разрыв 2 рода. В точке 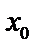 нет одного из односторонних пределов или если хотя бы один из односторонних пределов бесконечен.
нет одного из односторонних пределов или если хотя бы один из односторонних пределов бесконечен.
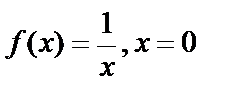 – точка разрыва 2 –го рода.
– точка разрыва 2 –го рода.
Глава 7. Производная и дифференциал
7.1. Физический и геометрический смысл производной
Геометрический смысл
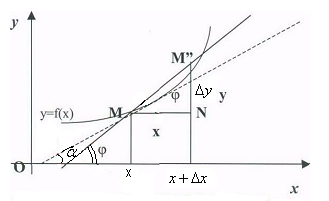
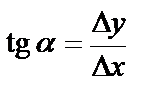 – тангенс угла наклона секущей.
– тангенс угла наклона секущей.
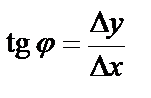 , если
, если 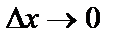 , то секущая переходит в касательную:
, то секущая переходит в касательную: 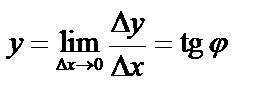 . Производная равна угловому коэффициенту касательной.
. Производная равна угловому коэффициенту касательной.
Физический смысл
Пусть 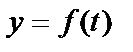 - закон движения математической точки, т.е. зависимость пути y от времени t. За время t пройден путь
- закон движения математической точки, т.е. зависимость пути y от времени t. За время t пройден путь 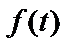 , а за
, а за 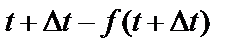 .
.
Отношение 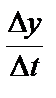 – средняя скорость движения; мгновенная скорость
– средняя скорость движения; мгновенная скорость 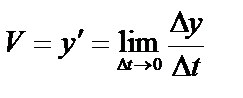 .
.
В общем, для любой функции 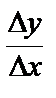 – средняя скорость изменения y относительно изменения x,
– средняя скорость изменения y относительно изменения x, 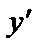 – мгновенная скорость изменения y при некотором x. С помощью производной можно оценить скорость изменения связанных величин.
– мгновенная скорость изменения y при некотором x. С помощью производной можно оценить скорость изменения связанных величин.
7.2. Определение производной. Свойства
Пусть дана функция 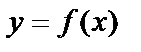 , возьмем значение аргумента x и зададим ему приращение
, возьмем значение аргумента x и зададим ему приращение 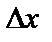 , это вызовет приращение функции
, это вызовет приращение функции 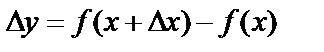 .
.
Производная: 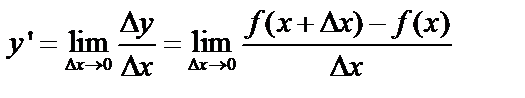 , т.к. при различных значениях x производная различна,
, т.к. при различных значениях x производная различна, 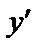 – функция аргумента x, т.е.
– функция аргумента x, т.е. 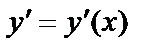 .
.
Пример. Вычислим производную 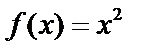 . Пусть x получил приращение
. Пусть x получил приращение 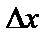 , тогда
, тогда 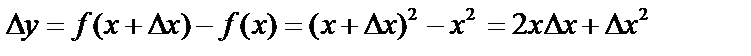 ;
; 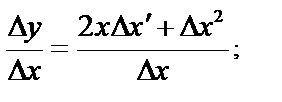
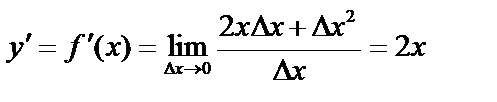 ; т.е.
; т.е. 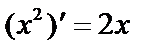 .
.
Свойства производной
1) Производная 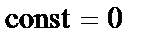 ,
, 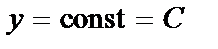 ,
, 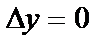 ,
, 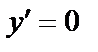 .
.
Пусть 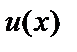 и
и 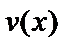 – две функции, имеющие производные.
– две функции, имеющие производные.
2) 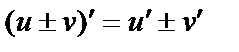 ;
;
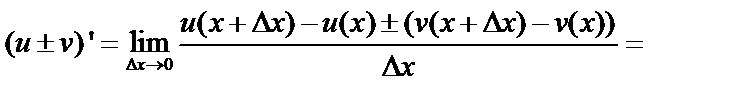
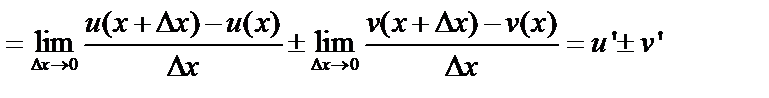 .
.
3) 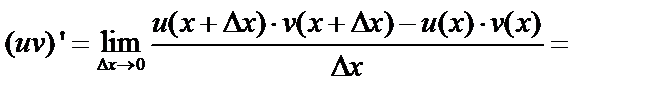
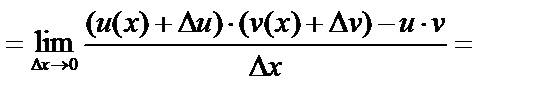
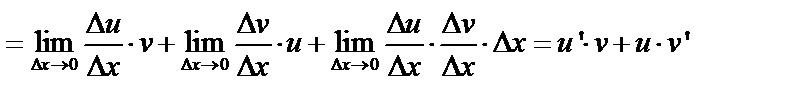 , т.е.
, т.е.
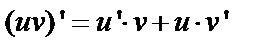 .
.
4). 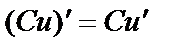 .
.
5) 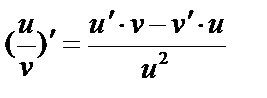 .
.
7.3. Производная сложной и обратной функций
Сложная функция
Пусть задана функция 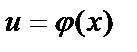 и функция
и функция 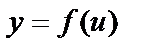 , тогда
, тогда 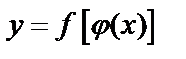 называется сложной функцией.
называется сложной функцией.
Пример. 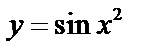 ;
; 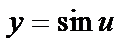 ;
; 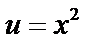 ;
; 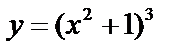 ;
; 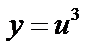 ;
; 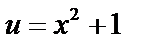 и т.д.
и т.д.
Пусть эти функции – дифференцируемые. Пусть x получил приращение 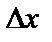 , тогда функции
, тогда функции 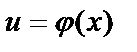 и
и 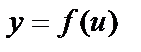 получают приращение
получают приращение 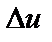 и
и 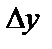 . Рассмотрим
. Рассмотрим 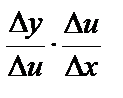 . Перейдем к пределу (если
. Перейдем к пределу (если 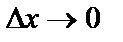 , то
, то 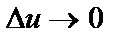 ):
): 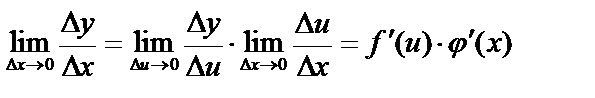 .
.
Обратная функция
Пусть 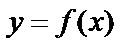 , будем считать y за аргумент, а x – за функцию. Тогда
, будем считать y за аргумент, а x – за функцию. Тогда 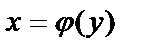 – обратная функция, может быть многозначной.
– обратная функция, может быть многозначной.
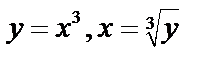 -обратная,
-обратная, 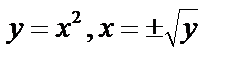 – двузначная функция и т.д.
– двузначная функция и т.д.
Если 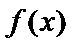 – монотонная функция, то существует непрерывная обратная функция
– монотонная функция, то существует непрерывная обратная функция 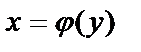 .
. 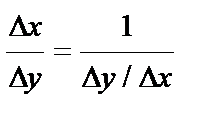 . Перейдя к пределу:
. Перейдя к пределу: 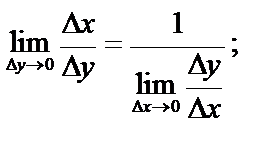
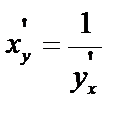 или
или 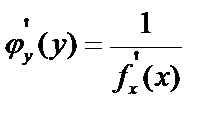 .
.
7.4. Производные тригонометрических функций
а) 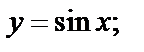
Воспользуемся схемой нахождения производной:
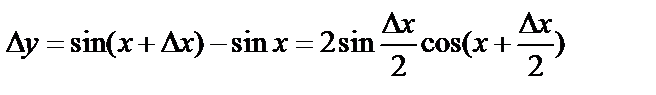 ;
; 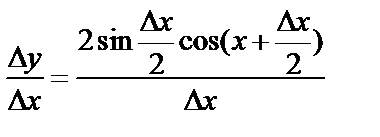 ;
;
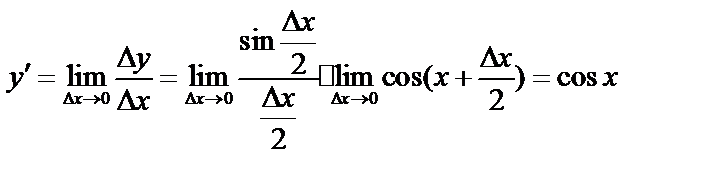 ;
;
(учли первый замечательный предел и непрерывность функции 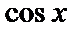 ).
).
Итак, 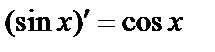 и
и 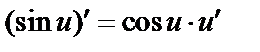 .
.
б) 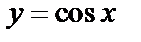 ;
; 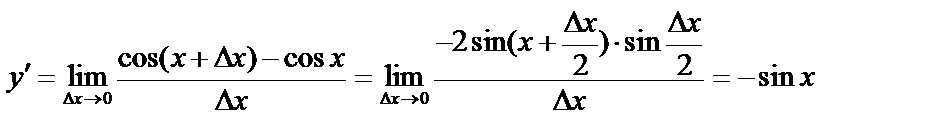 ;
;
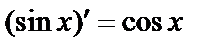 и
и 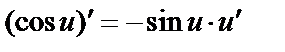 .
.
в) 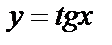 ;
;
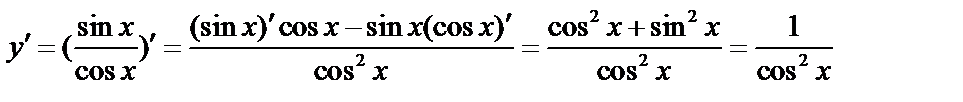 ;
;
т.е.
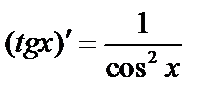 и
и 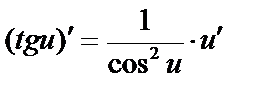 .
.
г) 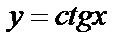 ;
; 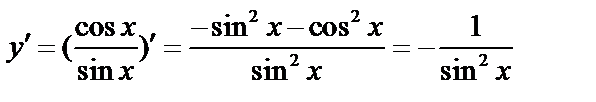 ;
;
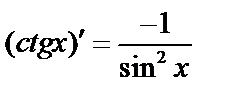 ;
; 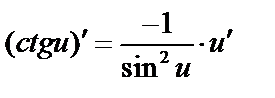 .
.
7.5. Производная обратных тригонометрических функций
а) 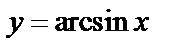 , где
, где 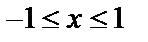 и
и 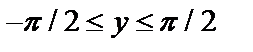 .
.
Обратная функция имеет вид 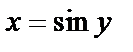 , причем
, причем 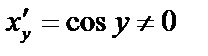 , если
, если 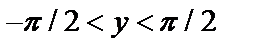 .
.
Используем правила дифференцирования обратной функции
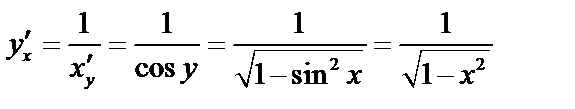 .
.
При 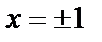 производная не существует.
производная не существует.
Итак, 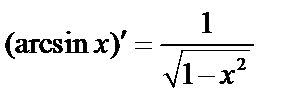 и
и 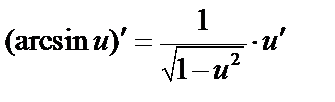 .
.
б) 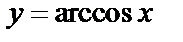 Поскольку
Поскольку 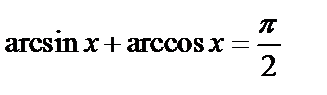 , то
, то 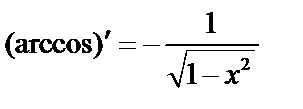 ;
; 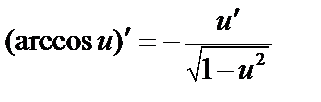 .
.
Аналогично, 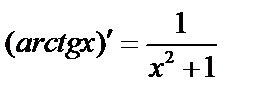 ;
; 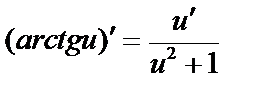 .
.
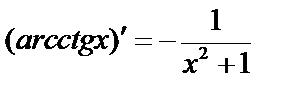 ;
; 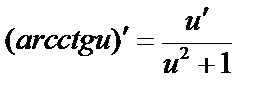 .
.
7.6. Производная показательной, логарифмической и степенной функций
Производная показательной функции
а) 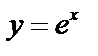 .
.
Прологарифмируем обе части равенства по основанию 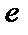 , получим
, получим 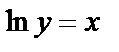 Дифференцируя обе части по переменной
Дифференцируя обе части по переменной 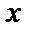 и учитывая, что
и учитывая, что 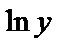 – сложная функция, получим
– сложная функция, получим 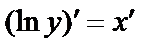 или
или 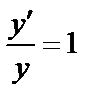 , откуда
, откуда 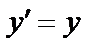 , т.е.
, т.е. 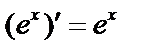 и
и 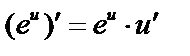 .
.
Заметим, что кривая 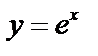 , называемая экспонентой, обладает отличающим только ее свойством: в каждой точке х ордината кривой
, называемая экспонентой, обладает отличающим только ее свойством: в каждой точке х ордината кривой 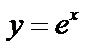 равна угловому коэффициенту (тангенсу угла наклона) касательной к кривой в этой точке:
равна угловому коэффициенту (тангенсу угла наклона) касательной к кривой в этой точке: 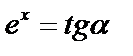 .
.
б) 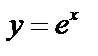 .
. 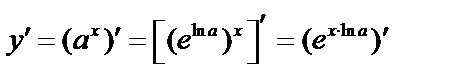 и по правилу дифференцирования сложной функции
и по правилу дифференцирования сложной функции 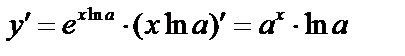 .
.
Итак, 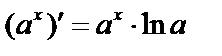 и
и 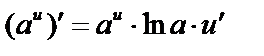 .
.
в) 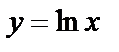 ;
; 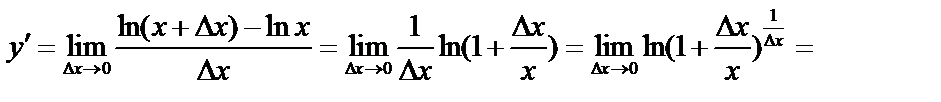
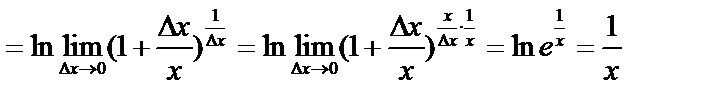 .
. 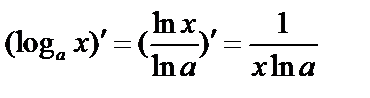 .
.
г) Производная степенной функции
Теперь мы можем доказать формулу производной степенной функции 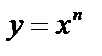 для любого
для любого 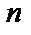 . Действительно,
. Действительно, 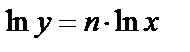 . Дифференцируя обе части равенства, получим
. Дифференцируя обе части равенства, получим 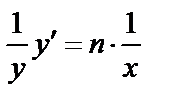 , откуда
, откуда 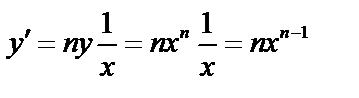 ,
, 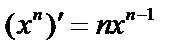 и
и 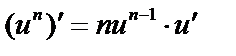 .
.
Таблица производных
| № п/п | Функция y | Производная 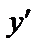
| № п/п | Функция у | Производная 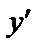
|
| 1 | 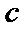
| 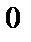
| 14 | 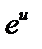
| 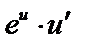
|
| 2 | 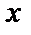
| 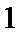
| 15 | 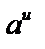
| 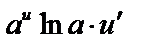
|
| 3 | 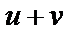
| 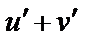
| 16 | 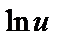
| 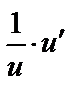
|
| 4 | 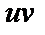
| 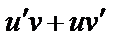
| 17 | 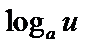
| 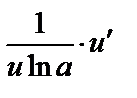
|
| 5 | 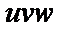
| 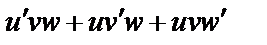
| 18 | 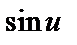
| 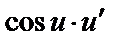
|
| 6 | 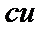
| 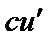
| 19 | 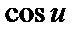
| 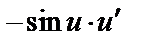
|
| 7 | 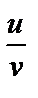
| 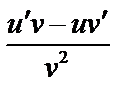
| 20 | 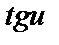
| 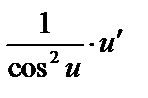
|
| 8 | 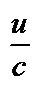
| 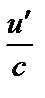
| 21 | 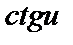
| 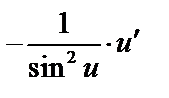
|
| 9 | 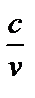
| 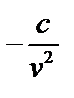
| 22 | 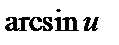
| 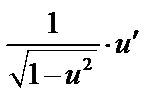
|
| 10 | 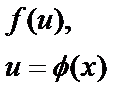
| 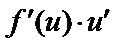
| 23 | 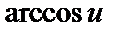
| 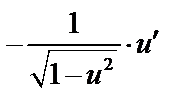
|
| 11 | 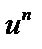
| 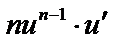
| 24 | 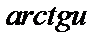
| 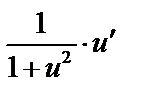
|
| 12 | 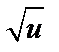
| 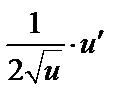
| 25 | 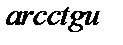
| 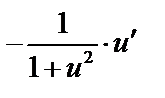
|
| 13 | 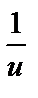
| 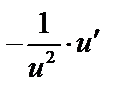
|
7.7. Логарифмическая производная.








