Уравнение плоскости в отрезках
Теорема. В декартовых координатах каждая плоскость определяется уравнением первой степени.
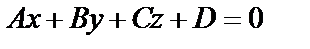 – общее уравнение плоскости, где
– общее уравнение плоскости, где 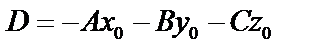 .
.
Справедливо и обратное: каждое уравнение первой степени определяет плоскость.
Уравнение плоскости в отрезках.
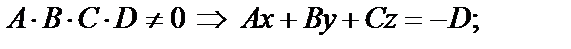
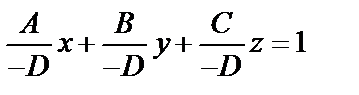 . Обозначим
. Обозначим 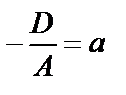
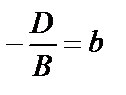
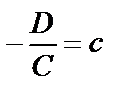
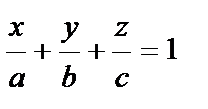 – уравнение плоскости в отрезках. Смысл величин а, b, c – это отрезки, которые плоскость отсекает от осей координат.
– уравнение плоскости в отрезках. Смысл величин а, b, c – это отрезки, которые плоскость отсекает от осей координат.
4.5. Расстояние от точки до плоскости
Пусть уравнение плоскости Р : 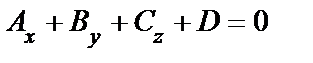 , дана
, дана 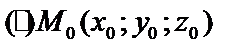 которая не принадлежит плоскости. Тогда
которая не принадлежит плоскости. Тогда 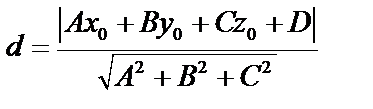 . Чтобы найти расстояние от точки до плоскости, следует подставить координаты этой точки в уравнение плоскости и полученную величину поделить на модуль вектора
. Чтобы найти расстояние от точки до плоскости, следует подставить координаты этой точки в уравнение плоскости и полученную величину поделить на модуль вектора 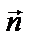 , т.е. на нормирующий множитель
, т.е. на нормирующий множитель 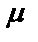 . Для определения расстояния от точки до плоскости можно пользоваться нормальным уравнением плоскости. В этом случае
. Для определения расстояния от точки до плоскости можно пользоваться нормальным уравнением плоскости. В этом случае 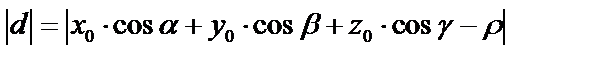 .
.
4.6. Уравнение плоскости, проходящей через 3 данных точки. Угол между плоскостями
Пусть точки 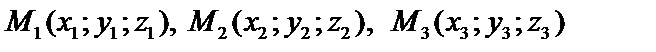 лежат в плоскости Р и точка
лежат в плоскости Р и точка 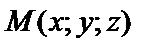 – любая точка плоскости. Тогда
– любая точка плоскости. Тогда 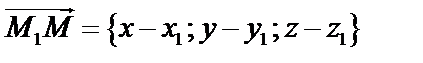 ,
, 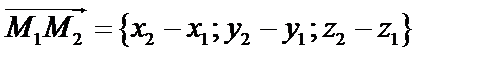 ,
, 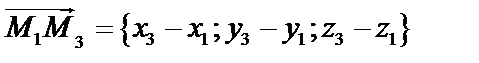 лежат в одной плоскости и являются компланарными. Условие компланарности: равенство нулю смешенного произведения:
лежат в одной плоскости и являются компланарными. Условие компланарности: равенство нулю смешенного произведения: 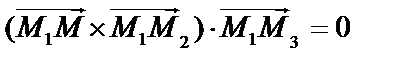 , т.е.
, т.е.
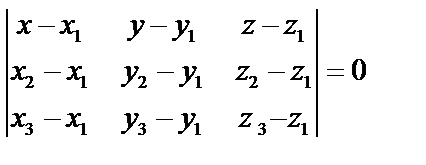 —уравнение плоскости, проходящей через 3 точки.
—уравнение плоскости, проходящей через 3 точки.
4.7. Прямая в пространстве
В общем случае прямую в пространстве можно рассматривать как линию пересечения 2-х плоскостей: 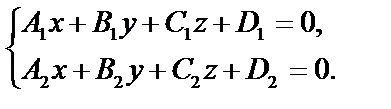
Канонические уравнения прямой
Пусть 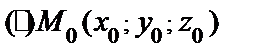 – точка лежащая на прямой;
– точка лежащая на прямой; 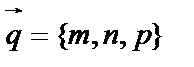 , где m, n, p – координаты направляющего вектора прямой, т.е. вектора параллельного данной прямой.
, где m, n, p – координаты направляющего вектора прямой, т.е. вектора параллельного данной прямой. 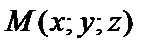 – текущая точка.
– текущая точка. 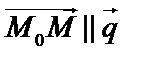 , получаем уравнение
, получаем уравнение 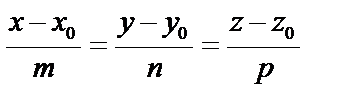 – канонические уравнения прямой.
– канонические уравнения прямой.
Чтобы перейти от общего уравнения прямой к каноническому, в качестве точки 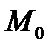 берут любое решение системы, направляющий вектор прямой можно найти как векторное произведение векторов нормалей
берут любое решение системы, направляющий вектор прямой можно найти как векторное произведение векторов нормалей 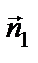 ×
× 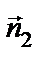 .
.
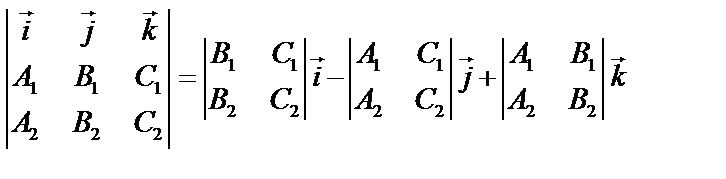 . Если направляющий вектор прямой задан точками M1, M2, то можно записать уравнение прямой, проходящей через 2 данные точки
. Если направляющий вектор прямой задан точками M1, M2, то можно записать уравнение прямой, проходящей через 2 данные точки 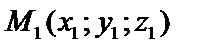 ,
, 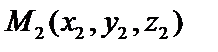 :
: 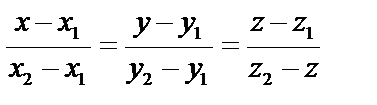 .
.
Угол между прямыми
Пусть 2 прямые заданы в канонической форме, т.е. известны направляющие векторы каждой прямой: 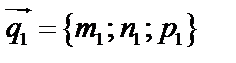 ,
, 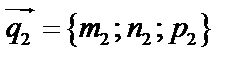 .
.
Угол 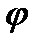 между прямыми равен углу между направляющими векторами:
между прямыми равен углу между направляющими векторами: 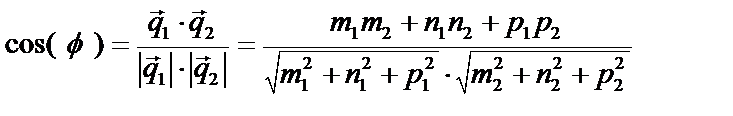 .
.
Если прямые параллельны, то 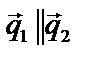 и
и 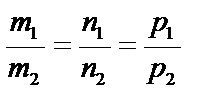 .
.
Если прямые перпендикулярны, 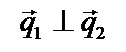 , то
, то 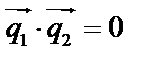 и
и 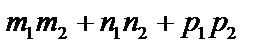 = 0 – условия перпендикулярности прямых.
= 0 – условия перпендикулярности прямых.
Кривые на плоскости
4.9. Окружность
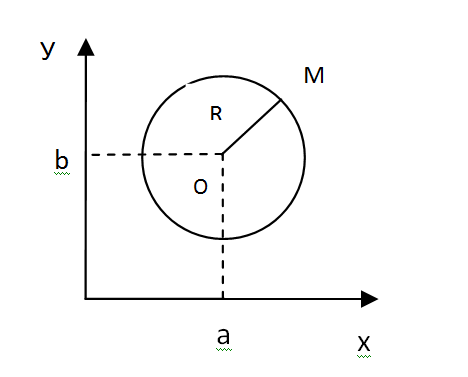
Окружность- это геометрическое место точек, каждая из которых отстоит от центра (О) на одинаковом расстоянии r. Пусть 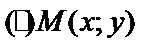 – текущая.
– текущая. 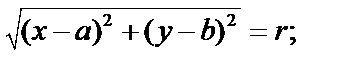
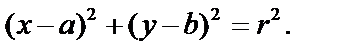
Центр окружности: 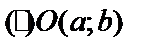 .
.
4.10. Эллипс
Эллипс – это геометрическое место точек, для которых сумма расстояний от двух фиксированных точек, называемых фокусами, есть величина постоянная (большая расстояния между фокусами).
Пусть 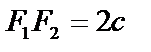 , тогда
, тогда 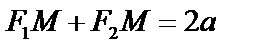 . Вводим
. Вводим 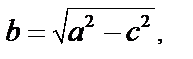
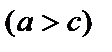 ,
,
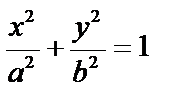 - каноническое уравнение эллипса.
- каноническое уравнение эллипса.
Эллипс симметричен относительно осей OX и OY ( x 2 и y 2 ). 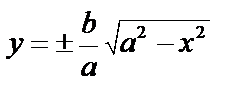
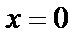 ,
, 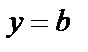 :
: 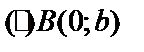 ;
; 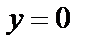 ,
, 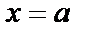 :
: 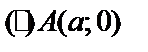 A , B , A * , B * – вершины эллипса, О – центр эллипса.
A , B , A * , B * – вершины эллипса, О – центр эллипса. 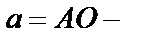 большая полуось,
большая полуось, 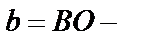 малая полуось.
малая полуось.
Эксцентриситет – отношение расстояния между фокусами к длине его большой оси: 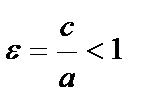 ;
; 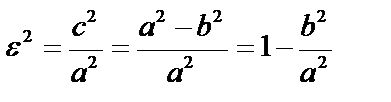 ;
; 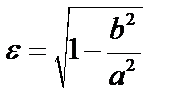 . Для окружности a = b и ε = 0, чем больше ε ,тем больше эллипс вытянут.
. Для окружности a = b и ε = 0, чем больше ε ,тем больше эллипс вытянут.
Эллипс получается при сечении цилиндра и проекция окружности на плоскость.
4.11. Гипербола
Гипербола – это геометрическое место точек, для которых разность расстояний от двух фиксированных точек, называемых фокусами, есть постоянная величина, взятая по модулю и меньше расстояния между фокусами.
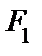 и
и 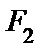 - фокусы
- фокусы 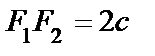 . Пусть
. Пусть 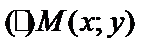 – текущая.
– текущая. 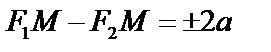
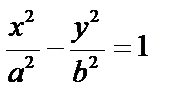 – каноническое уравнение гиперболы.
– каноническое уравнение гиперболы.
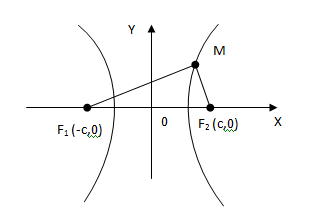
Прямые 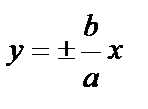 – асимптоты.
– асимптоты.
Эксцентриситет – отношение расстояния между фокусами гиперболы к расстоянию между ее вершинами, 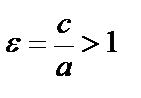 , характеризует форму гиперболы.
, характеризует форму гиперболы.
4.12. Парабола
Парабола – геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки – фокуса равно расстоянию до некоторой фиксированной прямой, называемой директрисой (не проходит через фокус). Фокус F, расстояние от F до директрисы равно p – параметр параболы. Начало координат – посередине между F и директрисой.
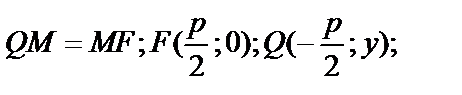
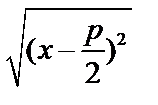 ,
, 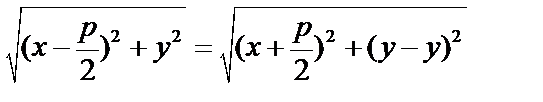 ,
, 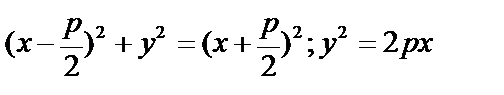 .
.
Парабола симметрична относительно ОХ. х=0, у=0. (у2<0),  . Пусть х=1, тогда
. Пусть х=1, тогда 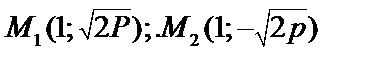 . Длина хорды параболы, проведенной перпендикулярно оси, равна
. Длина хорды параболы, проведенной перпендикулярно оси, равна 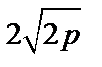 .
.
p характеризует «ширину» области, ограниченной параболой.
| Q |
| r |
| M |
| Y |
| d |
| p\2 |
| F (p\2,0) |
| X |
| 0 |
Глава 5. Функции
5.1. Понятие множества. Логическая символика
Множество – любая совокупность объектов, называемых элементами множества.
Примеры множеств – множество студентов академии, факультета, набор трех уравнений, множество всех целых чисел.
Множества обозначаются заглавными буквами, а элементы – строчными; 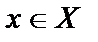 – х элемент множества X;
– х элемент множества X; 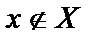 – x не является элементом множества X.
– x не является элементом множества X. 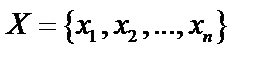 – множество Х состоит их элементов
– множество Х состоит их элементов 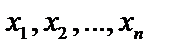 .
.
Пусть Х и Y – два множества. Если они состоят из одних и тех же элементов, то они совпадают, то есть Х=Y. Если каждый элемент множества Х является элементом множества Y, то 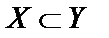 (Х содержится в Y) и Х – подмножество Y.
(Х содержится в Y) и Х – подмножество Y.
Множество, не содержащее ни одного элемента, называется пустым 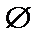 .
.
Пусть Х – множество, имеющее свойство Р(х), тогда 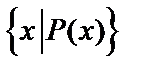 обозначает совокупность тех элементов Х, которые обладают свойством Р(х).
обозначает совокупность тех элементов Х, которые обладают свойством Р(х).
Объединением множеств А и В называется множество 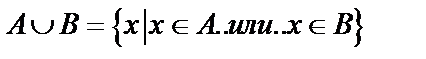 .
.
Пересечением множеств А и В называется множество 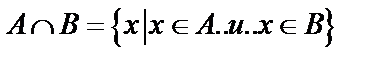 .
.
Разностью множеств А и В называется множество 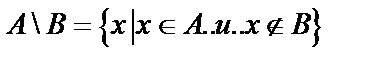 .
.
Верхняя и нижняя границы множества.
Говорят, что множество Х ограничено сверху (снизу), если существует число С такое, что для любого 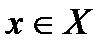 выполнено
выполнено 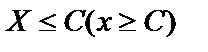 . С – верхняя (нижняя) грань множества Х. С=sup X – верхняя, C=inf X – нижняя.
. С – верхняя (нижняя) грань множества Х. С=sup X – верхняя, C=inf X – нижняя.
Логическая символика.
Пусть 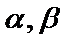 - некоторые утверждения. Тогда
- некоторые утверждения. Тогда 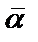 – не
– не 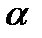 , то есть отрицание утверждения
, то есть отрицание утверждения 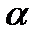 .
.
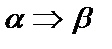 - из
- из 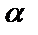 следует
следует 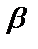 ;
; 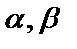 –
– 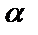 эквивалентно
эквивалентно 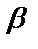 ;
;
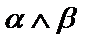 -
- 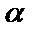 и
и 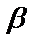 - конъюнкция;
- конъюнкция; 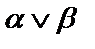 –
– 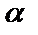 или
или 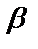 – дизъюнкция;
– дизъюнкция;
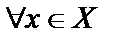
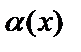 для всякого элемента
для всякого элемента 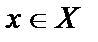 истинно утверждение
истинно утверждение 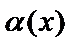 . (
. ( 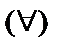 – квантор всеобщности);
– квантор всеобщности);
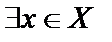
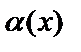 существует элемент
существует элемент 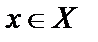 такой, что для него истинно утверждение
такой, что для него истинно утверждение 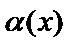 . (
. (  – квантор существования).
– квантор существования).
Принцип математической индукции: 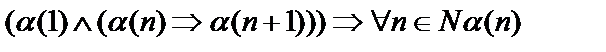 .
.
Числа.
Натуральные числа 1, 2,3,…- N.
Целые числа – Z, Z0 –множество всех неотрицательных чисел (и 0).
Q – множество рациональных чисел, x = m/n.
I – множество иррациональных чисел
R – множество действительных (вещественных) чисел, числовая прямая.
Модуль: 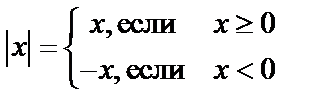 ;
; 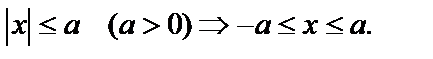 .
.
Если 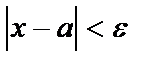 , то
, то 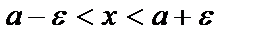 ; это называются
; это называются 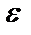 – окрестностью точки
– окрестностью точки 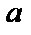 .
.
5.2. Понятие функции. Основные свойства функции
Часто приходится рассматривать изменение одной величины в зависимости от изменения другой. При изменении движения путь рассматривается как переменная, изменяющаяся в зависимости от времени. Путь – функция времени. Если радиус круга R принимает различные значения, то площадь 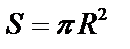 тоже будет принимать различные значения. S – функция R. Если каждому элементу x множества X ставится в соответствие определенный элемент y множества Y, то говорят, что на множестве X задана функция
тоже будет принимать различные значения. S – функция R. Если каждому элементу x множества X ставится в соответствие определенный элемент y множества Y, то говорят, что на множестве X задана функция 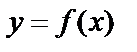 . х – независимая переменная, y—зависимая переменная.
. х – независимая переменная, y—зависимая переменная.
Частные значения получаются, если аргументу х придавать частные значения. Пусть 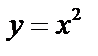 ,
, 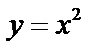 при
при 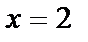 будет
будет 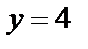 , при
, при 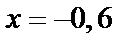
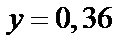 и так далее.
и так далее.
Запись: 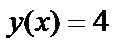 ;
; 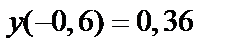 . Множество X – область определения (существования) функции, множество Y – область значений функции.
. Множество X – область определения (существования) функции, множество Y – область значений функции.
Способы задания функции
Три основных способа – аналитический, табличный, графический.
1. Аналитический способ состоит в том, что зависимость задается в виде формулы, указывающей, какие действия надо выполнить, чтобы получить значение функции 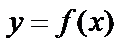 .
.
2. Табличный способ заключается в том, что в определенном порядке записываются значения х и соответствующие значения у. Конечное число аргументов.
3. Графический способ часто используется в практике физических измерений. Аргументы – абсциссы, функция – ординаты. Следовательно, график 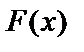 – множество точек плоскости.
– множество точек плоскости.
Рассмотрим основные свойства функции
1. 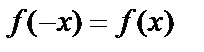 – функция чётная,
– функция чётная, 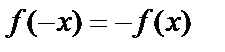 – функция нечётная.
– функция нечётная.
Если функция не является ни чётной, ни нечётной, то говорят, что функция общего вида.
2. Монотонность.
Функция называется возрастающей, если большему значению аргумента из множества X соответствует большее значение функции 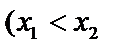 , то
, то 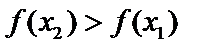 ).
).
Функция убывающая, если большему значению аргумента соответствует меньшее значение функции ( 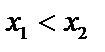 , то
, то 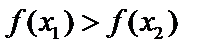 ).
).
3. Ограниченность.
Функция 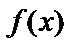 называется ограниченной на множестве X, если существует такое положительное число
называется ограниченной на множестве X, если существует такое положительное число 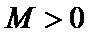 , что
, что 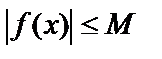 для любого
для любого 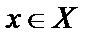 .
.
4. Периодичность.
Функция 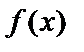 называется периодической с периодом
называется периодической с периодом 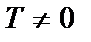 , если выполняется равенство
, если выполняется равенство 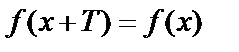 .
.
5.3. Основные элементарные функции
1. Степенная. 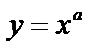 , где
, где 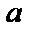 - действительное число.
- действительное число.
2. Показательная: 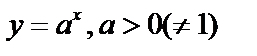 .
.
3. Логарифмическая: 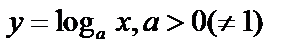 .
.
4. Тригонометрические: 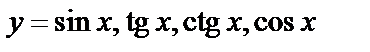 ;
;
5. Обратные тригонометрические функции: 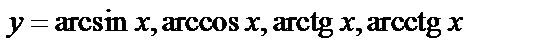 .
.
6. Сложная функция – функция вида 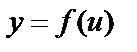 , где
, где 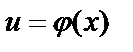 .
.
5.4. Элементарные функции. Классификация функций.
Элементарные функции – все функции, которые можно получить из основных элементарных функций с помощью:
а) алгебраических действий  и так далее;
и так далее;
б) операцией образования сложной функции.
Неэлементарные функции: 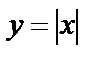 ;
; 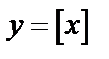 (антье) – целая часть числа х. [2,3]=2; [–2,5]=–3.
(антье) – целая часть числа х. [2,3]=2; [–2,5]=–3.
Элементарные функции можно разделить на алгебраические и трансцендентные (неалгебраические).
Алгебраической называется функция, в которой над аргументом производится конечное число алгебраических действий:
а) многочлен 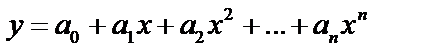 ;
;
б) дробно-рациональная функция – отношение двух многочленов;
в) иррациональная функция (если есть корни).
Всякая неалгебраическая функция называется трансцендентной. К числу трансцендентных относиться тригонометрические, показательные, логарифмические и т.д.








