Глава 4. Аналитическая геометрия
4.1. Общее уравнение прямой на плоскости
Теорема. В декартовой системе координат каждая прямая на плоскости определяется уравнением первой степени.
Общее уравнение прямой на плоскости в декартовых координатах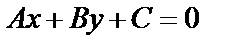 
. Если 
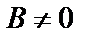, то 
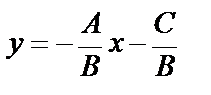, обозначив 
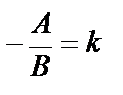и 
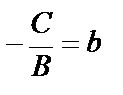, получим уравнение прямой 
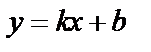с угловым коэффициентом 
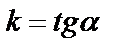, где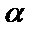 
– угол прямой с осью Оx; b – величина отрезка, отсеченного на оси Oy. Если 
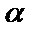=0, то прямая параллельна оси Ox и 
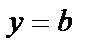. Если 
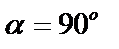, то прямая перпендикулярна Ox и 
.
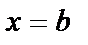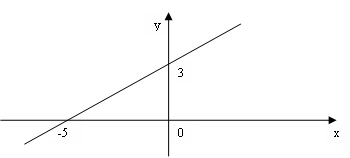
Пример.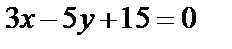 
; 
; 
.
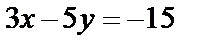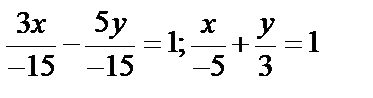Преобразуем: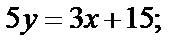 
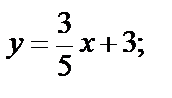
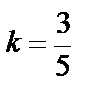– угловой коэффициент.
4.2. Уравнение прямой, проходящей через две точки. Угол между прямыми
Получим уравнение прямой, проходящей через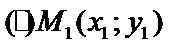 
с угловым коэффициентом k.
.
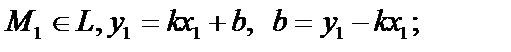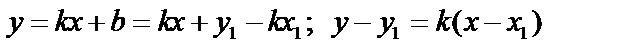(1)
Получим уравнение прямой, проходящей через две точки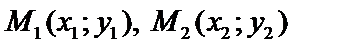 
.
Из предыдущего уравнения: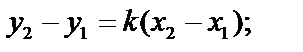 
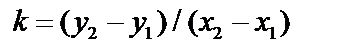. Подставим в (1):
.
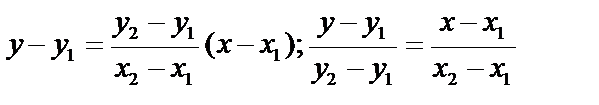Если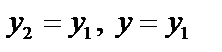 
(прямая параллельна оси ОХ), если 
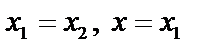(параллельна оси О Y).
Угол между прямыми с угловыми коэффициентами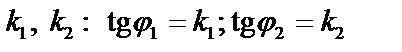 
. Угол между прямыми: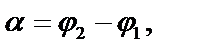 
.
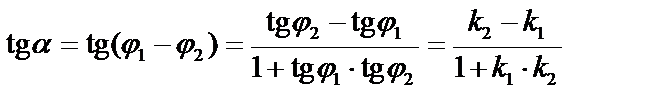Условие параллельности прямых: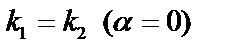 
; перпендикулярность: 
.
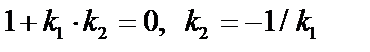4.3. Нормальное уравнение прямой. Расстояние от точки до прямой
Пусть дана прямая L. Проведем через начало координат прямую, перпендикулярную L: n – нормаль. На нормали введем положительное 
направление- от 
к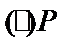 
. 
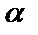– угол от оси ОХ до направления нормали, p – длина ОР. Считая 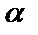и p известными, выведем уравнение прямой. Возьмем на прямой 
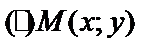. Очевидно, что 
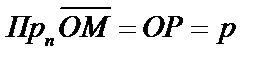. Пусть полярные координаты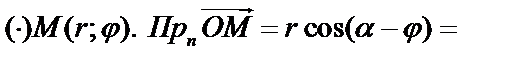 
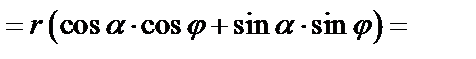
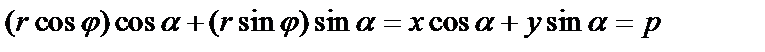или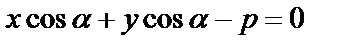 
– нормальное уравнение прямой (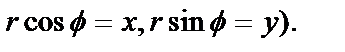 
Расстояние от (·) до прямой. Пусть L – прямая в нормальном виде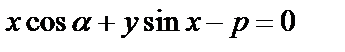 
. 
– лежит вне прямой. Определим d – расстояние от 
до прямой L. Через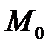 
проведем прямую 
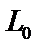,параллельную L. 
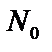– (·) пересечения 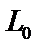с нормалью.
а) если 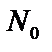лежит по ту же сторону от 0 , что и N, то нормальное уравнение прямой : 
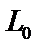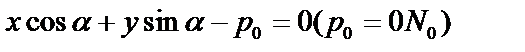т.к. 
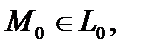то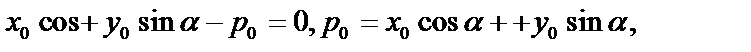 
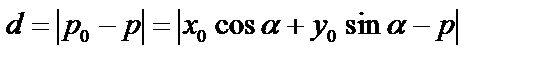-расстояние.
б) если лежит по другую сторону от О, то уравнение прямой : 
.
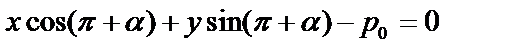
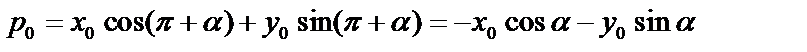Приведение общего уровня к нормальному.
Пусть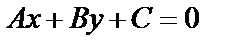 
– общее уравнение, а 
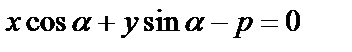– ее нормальное уравнение, т.к. эти уравнения определяют одну прямую, то их коэффициенты пропорциональны. Умножим все члены общего уровня на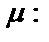 
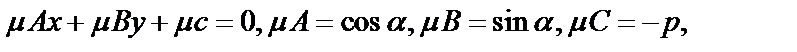первые два возведем в квадрат и сложим: 
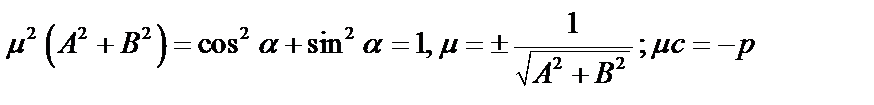<0, поэтому знак 
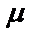берется противоположным знаку С. 
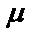– нормирующий множитель.
Пример. Дана прямая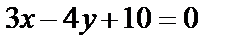 
и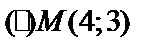 
. Найти расстояние d от М до прямой.
Приведем уравнение к нормальному виду: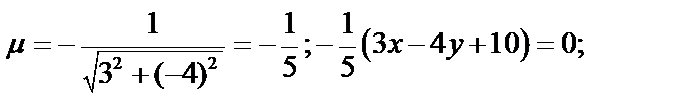 
.
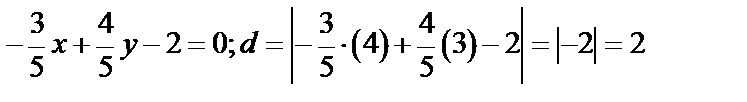4.4. Общее уравнение плоскости. Неполные уравнения плоскости.