Глава 2. Системы линейных алгебраических уравнений (СЛАУ)
2.1. Основные понятия и определения
В общем случае система n линейных с неизвестными уравнений имеет вид:
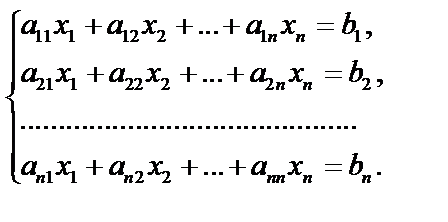 (2.1)
(2.1)
Через 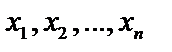 обозначены неизвестные, подлежащие определению; величины
обозначены неизвестные, подлежащие определению; величины 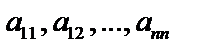 , называемые коэффициентами системы, и величины
, называемые коэффициентами системы, и величины 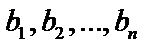 , называемые свободными членами, предполагаются известными. Каждый коэффициент системы имеет два индекса, первый из которых указывает номер уравнения, а второй – номер неизвестного, при котором стоит этот коэффициент. Решением системы называется всякая совокупность чисел
, называемые свободными членами, предполагаются известными. Каждый коэффициент системы имеет два индекса, первый из которых указывает номер уравнения, а второй – номер неизвестного, при котором стоит этот коэффициент. Решением системы называется всякая совокупность чисел 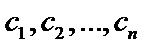 , которая, будучи подставлена в систему вместо неизвестных, превращает все уравнения системы в тождества. Система уравнений называется совместной, если она имеет хоты бы одно решение и несовместной, если она не имеет решений. Будем говорить, что совместная система – определенная, если она имеет единственное решение и неопределенная, если она имеет более одного решения.
, которая, будучи подставлена в систему вместо неизвестных, превращает все уравнения системы в тождества. Система уравнений называется совместной, если она имеет хоты бы одно решение и несовместной, если она не имеет решений. Будем говорить, что совместная система – определенная, если она имеет единственное решение и неопределенная, если она имеет более одного решения.
2.2. Условие совместимости СЛАУ. Теорема Кронекера-Капелли
Рассмотрим систему (10). Матрицей этой системы будем называть матрицу, составленную из ее коэффициентов: 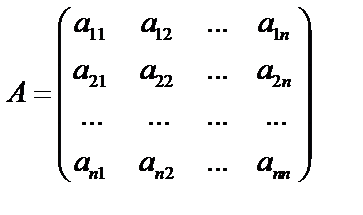 .
.
Если к этой матрице добавить столбец свободных членов, получим расширенную матрицу: 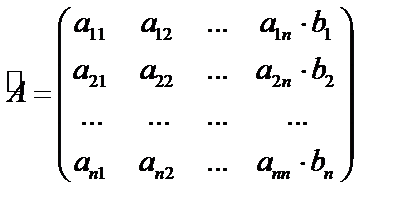
Теорема Кронекера–Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг расширенной матрицы равен рангу матрицы системы.
2.3. Правило Крамера решения СЛАУ
Рассмотрим систему n линейных уравнений с n неизвестными (2.1).
Введем матрицу неизвестных X 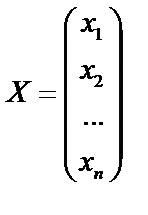 :, и матрицу свободных членов В:
:, и матрицу свободных членов В: 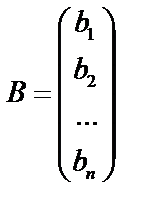 .
.
Считаем, что определитель матрицы системы (2.1) 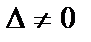 . Систему (2.1) можно заменить матричным уравнением:
. Систему (2.1) можно заменить матричным уравнением: 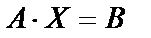 .
.
Умножим матричное уравнение слева на обратную матрицу 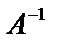 :
: 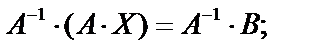 поскольку
поскольку 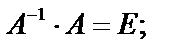 тогда
тогда 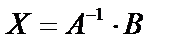 .
.
Используя формулу для обратной матрицы и введя обозначения: 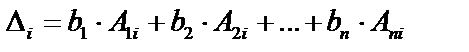 получаем формулы Крамера:
получаем формулы Крамера: 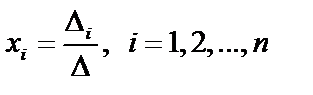 .
.
Определитель 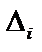 получается из определителя системы
получается из определителя системы  заменой его i столбца столбцом свободных членов (если расписать определитель
заменой его i столбца столбцом свободных членов (если расписать определитель 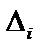 по i столбцу, мы получим формулу Крамера .
по i столбцу, мы получим формулу Крамера .
Например, для системы трех линейных уравнений с тремя неизвестными: если определитель системы 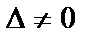 , то система имеет единственное решение:
, то система имеет единственное решение: 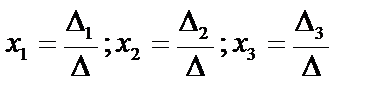 .
.
Пример 2.1. Решить систему 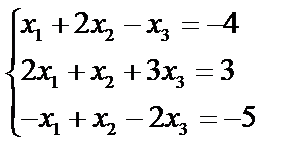
Необходимо вычислить четыре определителя по формулам Крамера:
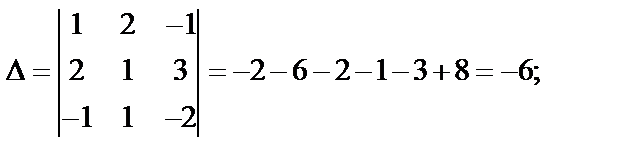
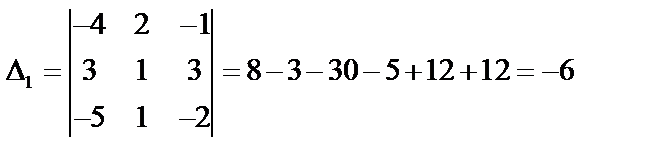 ;
;
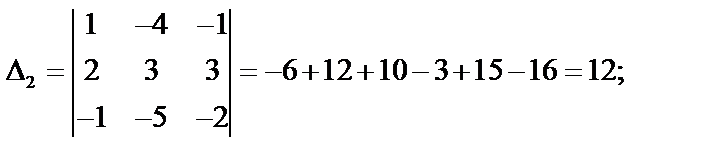
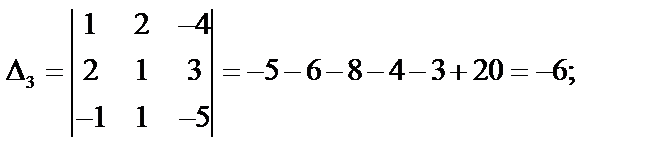
Тогда 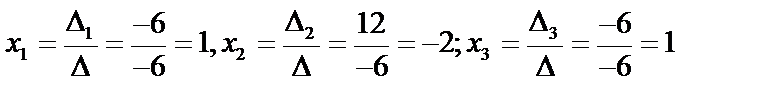 .
.
Проверкой убеждаемся в правильности вычислений.
2.4. Метод Гаусса
Рассмотрим систему n линейных уравнений с n неизвестными (2.1). Метод Гаусса представляет собой систематизированную схему последовательного исключения неизвестных. Пусть 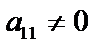 (иначе переставим местами уравнения). С помощью первого уравнения исключим переменную х1 из второго и последующих уравнений. Для этого от второго уравнения отнимем первое, умноженное на
(иначе переставим местами уравнения). С помощью первого уравнения исключим переменную х1 из второго и последующих уравнений. Для этого от второго уравнения отнимем первое, умноженное на 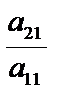 , от третьего – первое, умноженное на
, от третьего – первое, умноженное на 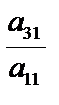 и т.д. Получим систему уравнений с новыми коэффициентами. Пусть
и т.д. Получим систему уравнений с новыми коэффициентами. Пусть 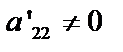 , тогда аналогично исключим х2 из третьего и последующих уравнений. Для этого умножим второе уравнение на
, тогда аналогично исключим х2 из третьего и последующих уравнений. Для этого умножим второе уравнение на 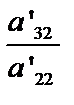 и вычтем полученный результат из третьего, из четвертого уравнения вычтем второе, умноженное на
и вычтем полученный результат из третьего, из четвертого уравнения вычтем второе, умноженное на 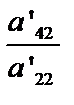 и т.д. Продолжив дальнейшее исключение неизвестных, получим систему с так называемой треугольной матрицей:
и т.д. Продолжив дальнейшее исключение неизвестных, получим систему с так называемой треугольной матрицей:
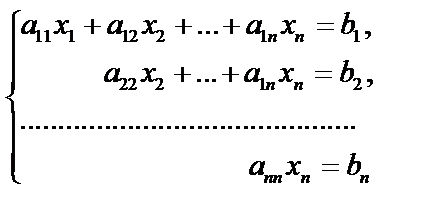
Эта процедура называется прямым ходом метода Гаусса. Далее начинаем обратный ход метода Гаусса, т.е. нахождение неизвестных. Находим 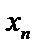 из последнего уравнения, затем найденное значение
из последнего уравнения, затем найденное значение 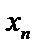 подставляем в предпоследнее уравнение и определяем xn–1. Найденные значения
подставляем в предпоследнее уравнение и определяем xn–1. Найденные значения 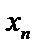 и
и 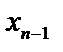 подставляем в (n – 2)-е уравнение и находим
подставляем в (n – 2)-е уравнение и находим 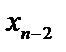 . Продолжая этот процесс, определяем остальные неизвестные системы.
. Продолжая этот процесс, определяем остальные неизвестные системы.
Мы полагали, что 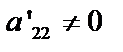 . Однако, при данных преобразованиях мы можем получить уравнения вида
. Однако, при данных преобразованиях мы можем получить уравнения вида 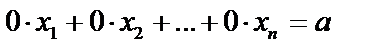 , в котором все коэффициенты при неизвестных равны 0. При этом возможны два случая.
, в котором все коэффициенты при неизвестных равны 0. При этом возможны два случая.
Если 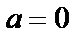 , то система имеет бесконечное количество решений. При этом одно (или несколько) уравнений являются следствием остальных.
, то система имеет бесконечное количество решений. При этом одно (или несколько) уравнений являются следствием остальных.
Если 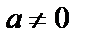 , то система не имеет решений.
, то система не имеет решений.
Как отыскивать решения системы в первом случае, будет указано в следующем пункте. При решении систем линейных уравнений методом Гаусса удобно приводить к треугольному (или ступенчатому) виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя все преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Пример 2.2. Решить систему из примера 2.1 методом Гаусса
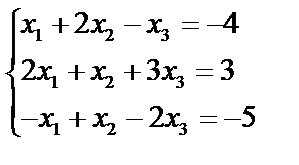
Запишем расширенную матрицу системы: 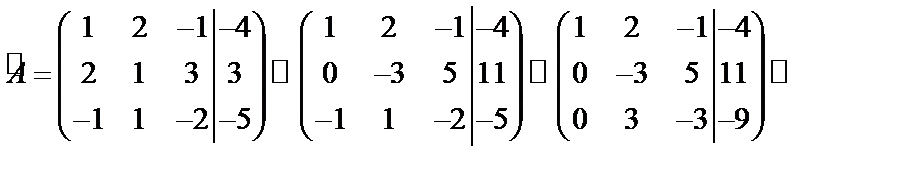
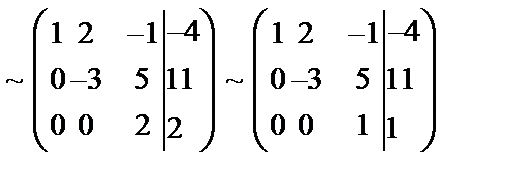 . В результате прямого хода матрица системы приведена к треугольному виду и найдено, что
. В результате прямого хода матрица системы приведена к треугольному виду и найдено, что 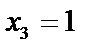 . Получим единичную матрицу, т.е. накопим нули выше главной диагонали:
. Получим единичную матрицу, т.е. накопим нули выше главной диагонали:
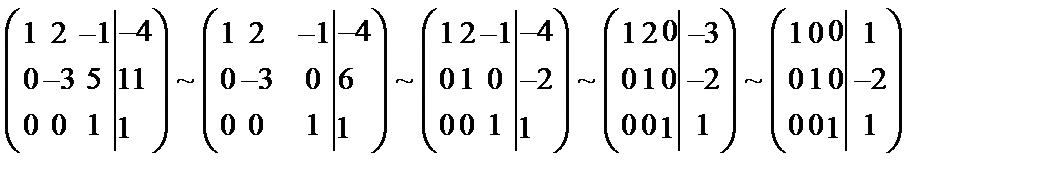 . Таким образом,
. Таким образом, 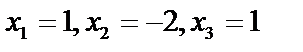 .
.
2.5. Матричные уравнения
Дана система n линейных уравнений с n неизвестными (2.1). Введём обозначения:
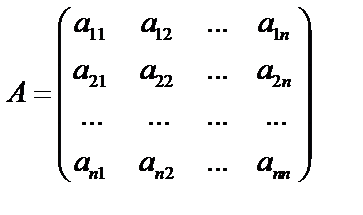 ,
, 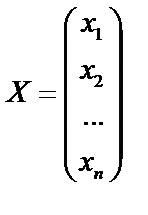 ,
, 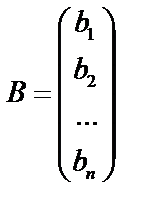 , тогда данную систему можно записать в матричном виде:
, тогда данную систему можно записать в матричном виде: 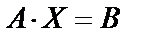 . Умножим это уравнение на обратную матриц
. Умножим это уравнение на обратную матриц 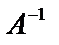 слева (считаем, что определитель матрицы системы не равен 0). Тогда:
слева (считаем, что определитель матрицы системы не равен 0). Тогда: 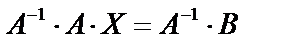 , т.к.
, т.к. 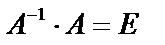 , тогда
, тогда 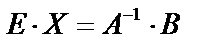 или
или 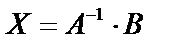 . Это формула для решения уравнения (2.1) с помощью обратной матрицы.
. Это формула для решения уравнения (2.1) с помощью обратной матрицы.
Если в уравнении 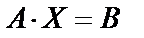 все три матрицы являются квадратными, причем
все три матрицы являются квадратными, причем 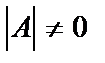 , тогда решение
, тогда решение 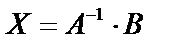 .
.
Рассмотрим матричное уравнение вида 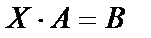 . Имеем
. Имеем 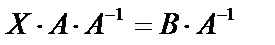 ;
; 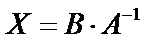 .
.
Пример 2.4. Решить систему примера 2.1 матричным способом (с помощью обратной матрицы).
Матрица системы 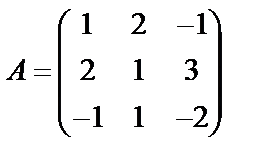 , матрица неизвестных
, матрица неизвестных 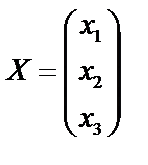 , матрица свободных членов
, матрица свободных членов 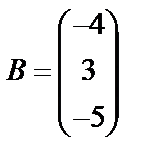 .
.
Найдем обратную матрицу 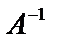 .
. 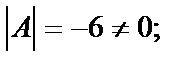 вычислим алгебраические дополнения:
вычислим алгебраические дополнения:
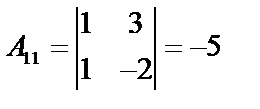 ;
; 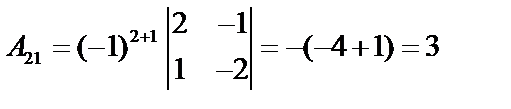 ;
; 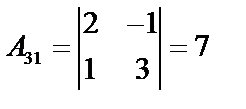 ;
; 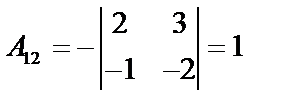 ;
; 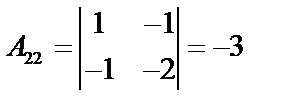 ;
; 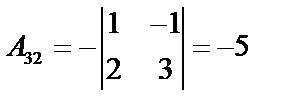 ;
; 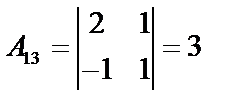 ;
; 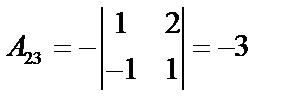 ;
; 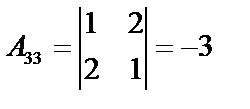 .
.
Тогда решение системы определены по формуле 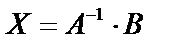 :
: 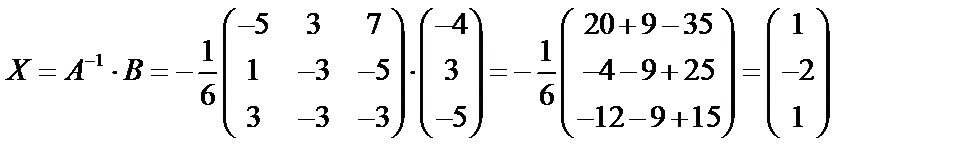
т.е. 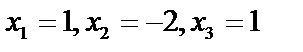 .
.
Глава 3. Векторы
3.1. Понятие вектора. Линейные операции над векторами
Различают скалярные и векторные величины. Скалярные величины полностью характеризуются своим численным значением в выбранной системе единиц (работа, температура, плотность и т.д.). векторы кроме численного значения, обладают направлением в пространстве. Вектором называется направленный отрезок 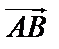 с начальной точкой А и конечной точкой В. Вектор может обозначаться одной буквой:
с начальной точкой А и конечной точкой В. Вектор может обозначаться одной буквой: 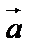 . Длиной (модулем) |
. Длиной (модулем) | 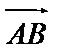 | вектора
| вектора 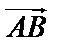 называется число, равное длине отрезка АВ.
называется число, равное длине отрезка АВ.
Векторы, лежащие на одной прямой (или на параллельных прямых) называются коллинеарными. Если начало и конец вектора совпадают, то такой вектор называют нулевым и обозначают 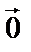 . |
. | 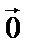 | = 0, направление
| = 0, направление 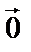 произвольно. Если
произвольно. Если 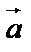 =
= 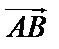 , то вектор
, то вектор 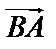 называют противоположным к вектору
называют противоположным к вектору 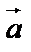 и обозначают –
и обозначают – 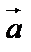 . Очевидно, что
. Очевидно, что 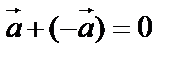 .
.
Введем в рассмотрение прямоугольную систему координат и перенесем вектор 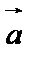 параллельно самому себе так, чтобы его начало совпало с началом координат. Координатами вектора
параллельно самому себе так, чтобы его начало совпало с началом координат. Координатами вектора 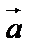 будем называть координаты его конечной точки:
будем называть координаты его конечной точки: 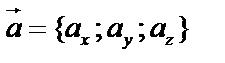 .
.
Модуль вектора 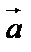 :
: 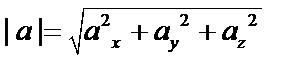 .
.
Линейные операции над векторами.
Пусть заданы векторы 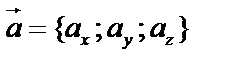 и
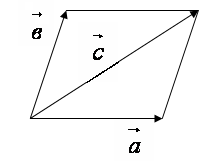
и 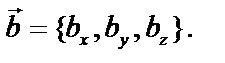 Линейными операциями называют сложение (вычитание) векторов и умножение вектора на скаляр. Сложение векторов производят по правилу параллелограмма:
Линейными операциями называют сложение (вычитание) векторов и умножение вектора на скаляр. Сложение векторов производят по правилу параллелограмма:
 ,
, 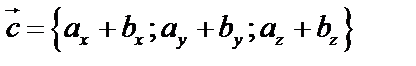 . Чтобы построить сумму векторов
. Чтобы построить сумму векторов 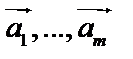 , нужно к концу вектора
, нужно к концу вектора 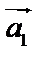 приложить вектор,
приложить вектор, 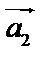 к концу вектора
к концу вектора 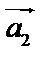 приложить вектор
приложить вектор 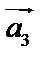 и так далее до
и так далее до 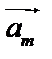 . Тогда суммой
. Тогда суммой 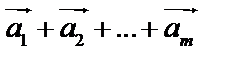 будет вектор, идущий из начала
будет вектор, идущий из начала 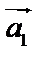 в конец вектора
в конец вектора 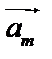 .
.
Вычесть какой-нибудь вектор – значит прибавить противоположный, т.е. 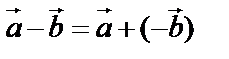 .
.
Умножение вектора 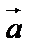 на (скаляр) число
на (скаляр) число 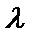 :
: 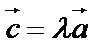 ,
, 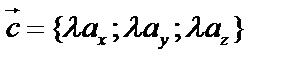 .
.
Если 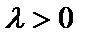 , то полученный вектор – это вектор, получающийся из
, то полученный вектор – это вектор, получающийся из 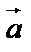 растяжением в
растяжением в 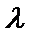 раз без изменения направления. Если
раз без изменения направления. Если 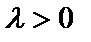 , тогда следует
, тогда следует 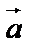 растянуть в
растянуть в 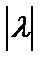 раз и изменить направление на противоположное.
раз и изменить направление на противоположное.
Свойства:
1. 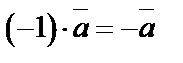 ;
;
2. 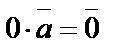 ;
;
3. 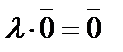 ;
;
4. 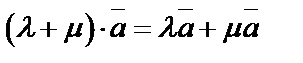 ;
;
5. 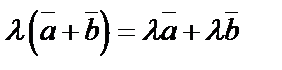 ;
;
6. 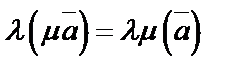 .
.
3.2. Линейно зависимые и линейно независимые векторы. Базис
Линейная комбинация векторов. Пусть даны векторы 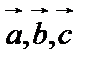 . Тогда всякий вектор, имеющий вид
. Тогда всякий вектор, имеющий вид 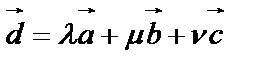 , где
, где 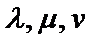 – некоторые числа, называется линейной комбинацией векторов
– некоторые числа, называется линейной комбинацией векторов 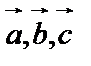 или вектор
или вектор 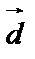 линейно выражается через векторы
линейно выражается через векторы 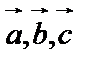 .
.
Данные векторы называются линейно-зависимыми, если какой-либо из этих векторов линейно выражается через остальные, в противном случае – эти векторы линейно независимые.
Два вектора линейно зависимы тогда и только тогда, если они коллинеарны друг другу. Из определения умножения вектора на число следует: если 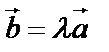 , то
, то 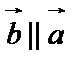 . Наоборот, если два вектора параллельны, то любой из них можно растянуть во столько раз, чтобы получить другой.
. Наоборот, если два вектора параллельны, то любой из них можно растянуть во столько раз, чтобы получить другой.
Три вектора линейно зависимы тогда и только тогда, когда они компланарны (параллельны одной плоскости).
Четыре или более векторов всегда линейно зависимы.
Тогда 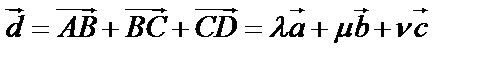 – разложение вектора по трем некомпланарным векторам (разложение вектора по трем осям), что можно осуществить единственным образом.
– разложение вектора по трем некомпланарным векторам (разложение вектора по трем осям), что можно осуществить единственным образом.
Совокупность линейно независимых векторов, по которым производится разложение остальных векторов, называется базисом. В плоскости базисом могут служить два неколлинеарных вектора, в пространстве – три некомпланарных вектора.
Пусть 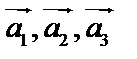 – базис,
– базис, 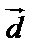 – произвольный вектор, тогда
– произвольный вектор, тогда 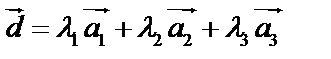 , где
, где 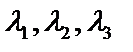 –координаты вектора
–координаты вектора 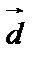 в базисе векторов
в базисе векторов 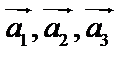 .
.
Обычно выбирают ортонормированный базис, в котором векторы ортогональны (перпендикулярны) и каждый вектор имеет единичную длину. В этом случае базисные векторы называют ортами и обозначают 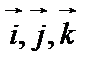 .
.
Декартовы координаты в пространстве
В качестве базиса декартовых координат выбрали три вектора единичной длины (орты), которые взаимно перпендикулярны и отнесены к общему началу в точке О, принятой за начало координат. Положение произвольной точки М в пространстве полностью характеризуется вектором 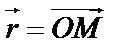 , называемым радиус-вектором точки М:
, называемым радиус-вектором точки М: 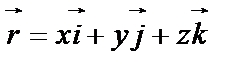 ,
, 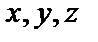 - декартовы координаты. Для любого вектора
- декартовы координаты. Для любого вектора 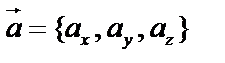 :
: 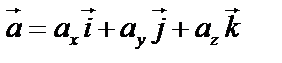 ,
, 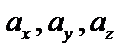 - проекции
- проекции 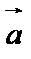 на соответствующие оси.
на соответствующие оси.
Если 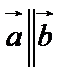 , то
, то 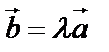 , тогда
, тогда 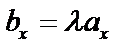 ,
, 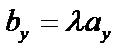 ,
, 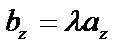 ,
, 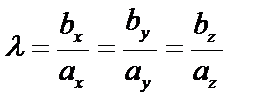 – условие коллинеарности векторов.
– условие коллинеарности векторов.
Если 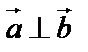 , то
, то 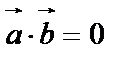 или
или 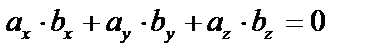 – условие ортогональности векторов.
– условие ортогональности векторов.
Направляющие косинусы вектора – косинусы углов, которые он образует с осями координат. Если 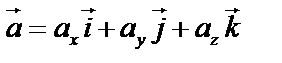 , то
, то 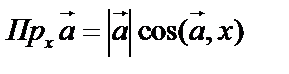 , то есть
, то есть 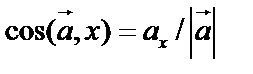 ,
, 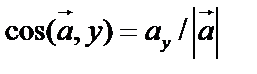 ,
, 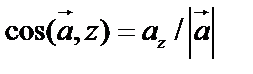 .
.
3.3. Скалярное произведение векторов
Скалярное произведение векторов 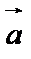 и
и 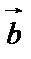 равно произведению модулей этих векторов на косинус угла
равно произведению модулей этих векторов на косинус угла 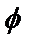 между ними:
между ними: 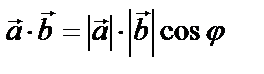 – скаляр. Иначе:
– скаляр. Иначе: 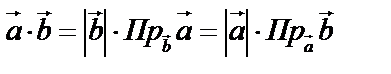 . Пример из физики:
. Пример из физики: 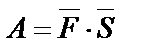 , А – работа,
, А – работа, 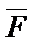 – сила,
– сила, 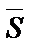 – перемещение.
– перемещение.
Свойства скалярного произведения:
1. Скалярное произведение равно 0, если векторы перпендикулярны, то есть 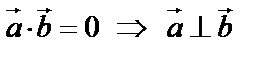 ,
, 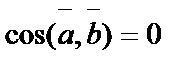 , α = 900. Если
, α = 900. Если 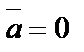 , то
, то 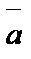 и
и 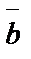 тоже перпендикулярны.
тоже перпендикулярны.
2. 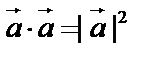 , так как
, так как 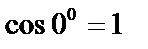 скалярный квадрат вектора равен квадрату его модуля.
скалярный квадрат вектора равен квадрату его модуля.
3. Перестановочный закон: 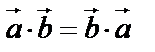 .
.
4. Распределительный закон: 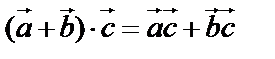 .
.
5. 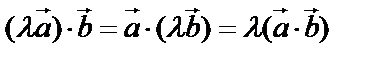 .
.
Пример:
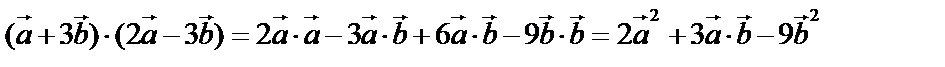 .
.
Пусть даны два вектора: 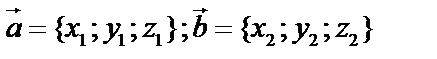 . Тогда скалярное произведение равно
. Тогда скалярное произведение равно 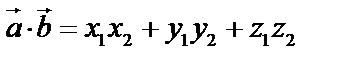
3.4. Векторное произведение векторов
Пусть дана тройка некомпланарных векторов 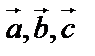 с общим началом, причем
с общим началом, причем 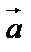 – первый вектор,
– первый вектор, 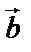 – второй,
– второй, 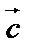 – третий. Такая тройка называется правой, если поворот от
– третий. Такая тройка называется правой, если поворот от 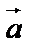 к
к 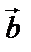 осуществляется против часовой стрелки, если смотреть с конца вектора
осуществляется против часовой стрелки, если смотреть с конца вектора 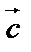 . Тройка называется левой, если поворот от
. Тройка называется левой, если поворот от 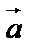 к
к 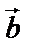 осуществляется по часовой стрелки. Если
осуществляется по часовой стрелки. Если 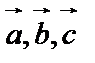 – правая, то
– правая, то 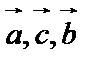 – левая.
– левая.
При циклической перестановке «смысл» тройки не меняется: если 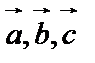 – правая тройка, то
– правая тройка, то 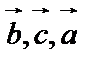 – правая, и
– правая, и 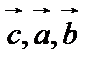 – правая.
– правая.
Векторным произведением векторов 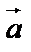 и
и 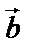 называется вектор
называется вектор 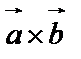 , определяемый следующими условиями:
, определяемый следующими условиями:
1. 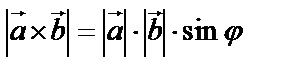 ,
, 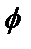 – угол между векторами – это площадь параллелограмма, построенного на этих векторах
– угол между векторами – это площадь параллелограмма, построенного на этих векторах
2. 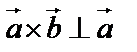 и
и 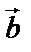 ;
;
3. упорядоченная тройка 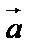 ,
, 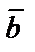 ,
, 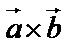 – правая.
– правая.
Свойства:
1. если 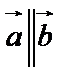 , то
, то 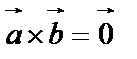 и
и 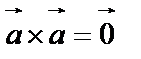 ;
;
2. 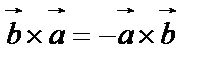 – S не меняется, меняется направление;
– S не меняется, меняется направление;
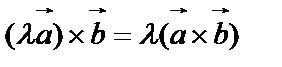 - если сторону параллелограмма увеличить в
- если сторону параллелограмма увеличить в 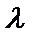 раз, то S тоже увеличится в
раз, то S тоже увеличится в 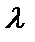 раз;
раз;
3. 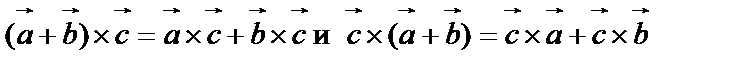 .
.
Эти свойства дают возможность раскрывать скобки. Например: 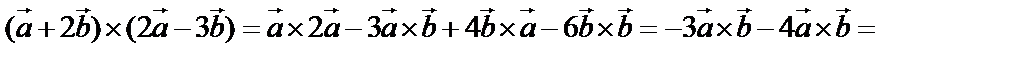
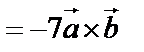
4. 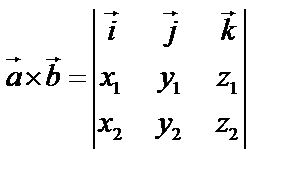 – это выражение векторного произведения через координаты векторов, где векторы:
– это выражение векторного произведения через координаты векторов, где векторы: 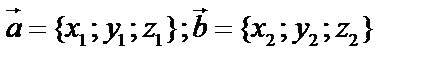 .
.
3.5. Смешанное произведение трех векторов
Пусть даны три вектора: 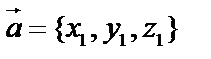 ,
, 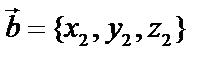 ,
, 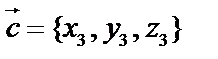 . Тогда смешанное (или векторно-скалярное) произведение –
. Тогда смешанное (или векторно-скалярное) произведение – 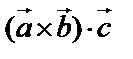 – скалярная величина, т.е. первые два вектора умножаются векторно, а результат – скалярно на третий вектор.
– скалярная величина, т.е. первые два вектора умножаются векторно, а результат – скалярно на третий вектор.
Геометрический смысл – 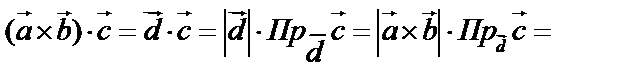
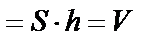 – объем параллелепипеда, построенного на векторах
– объем параллелепипеда, построенного на векторах  , которые образуют правую тройку. Если тройка левая, то
, которые образуют правую тройку. Если тройка левая, то 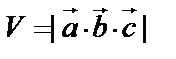 .
.
Свойства:
1. 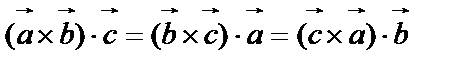 – при циклической перестановке множителей смешанное произведение не меняется (не меняется параллелепипед).
– при циклической перестановке множителей смешанное произведение не меняется (не меняется параллелепипед).
2. 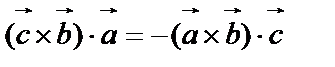 – знак меняется при перестановке двух сомножителей.
– знак меняется при перестановке двух сомножителей.
3. 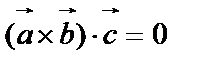 , когда
, когда 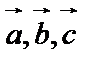 компланарны. Действительно, параллелепипед выражается чисто в плоскость и
компланарны. Действительно, параллелепипед выражается чисто в плоскость и 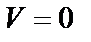 .
.
4. 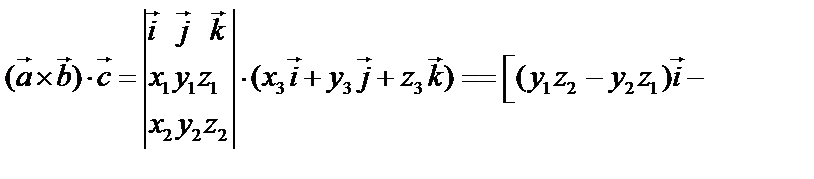
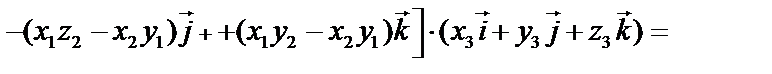
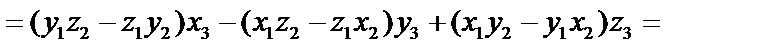
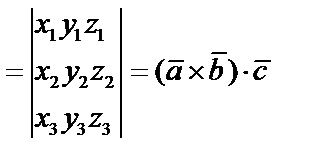
Это выражение смешанного произведения через координаты векторов.
5. Векторы 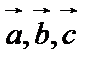 компланарны, если
компланарны, если 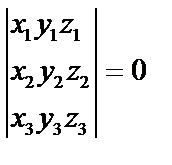 . Обычно смешанное произведение обозначают
. Обычно смешанное произведение обозначают 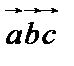 .
.








