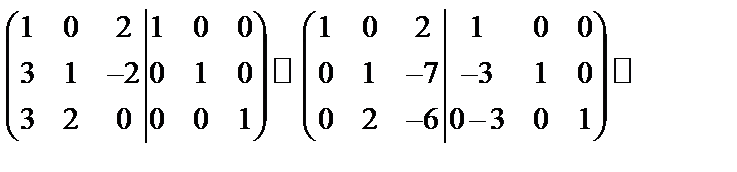По математике для студентов 1-го курса
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Белгородский государственный технологический университет
им В.Г. Шухова
Утверждено
научно-методическим советом
университета
ЭЛЕКТРОННЫЕ ЛЕКЦИИ
ПО МАТЕМАТИКЕ ДЛЯ СТУДЕНТОВ 1-ГО КУРСА
ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ
ВСЕХ НАПРАВЛЕНИЙ
Белгород 2015
Глава 1. Матрицы и определители
1.1.Понятие матрицы
Прямоугольная таблица, состоящая из чисел, расположенных в m строках и n столбцах, называется матрицей. Матрицы обозначаются заглавными латинскими буквами, например: 
.
Числа m и n называются порядками матрицы. Если m = n, то матрица называется квадратной порядка n , иначе – прямоугольной. Числа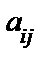 
, входящие в состав матрицы, называются ее элементами, причем
i – номер строки, j – номер столбца.
Строчная матрица имеет размер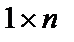 
, а столбцовая матрица – 
.
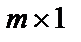Матрица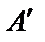 
, полученная из матрицы А заменой в ней строк на столбцы с сохранением порядка их следования, называется транспонированной. Очевидно, что 
.
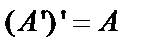Главная диагональ квадратной матрицы – воображаемая прямая, проходящая через элементы с одинаковыми индексами из левого верхнего в правый нижний ее угол. Эти элементы – диагональные. Побочная диагональ – прямая, идущая из правого верхнего в нижний левый угол матрицы.
Квадратная матрица, у которой все элементы вне главной диагонали равны 0 , называется диагональной. Среди диагональных элементов может быть и нулевые.
Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны 1, например: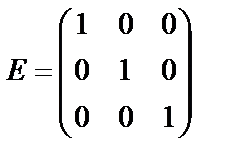 
– единичная матрица третьего порядка.
1.2. Основные операции над матрицами
Две матрицы называются равными, если эти матрицы имеют одинаковые порядки и все соответствующие их элементы совпадают.
Произведением матрицы А размером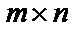 
на действительное число 
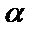называется матрица С размером 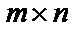, элементы 
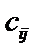которой равны 
.
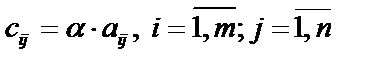Умножение матриц на число обладает следующими свойствами: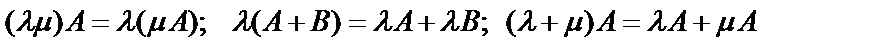 
.
Суммой двух матриц А и В размером 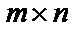называется матрица С размером 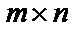, элементы 
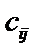которой равны 
.
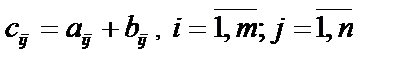Очевидно, что сложение матриц обладает следующими свойствами:
.
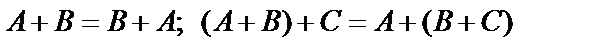Произведением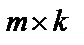 
матрицы А на 
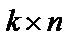матрицу В называется 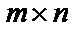матрица С, элементы 
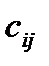которой равны сумме произведений элементов i строки матрицы А на соответствующие элементы j столбца матрицы В: 
.
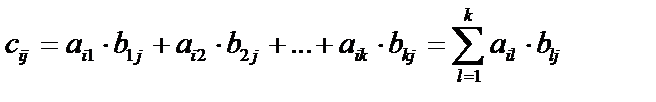Произведение матриц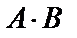 
имеет смысл в том случае, если число столбцов матрицы А совпадает с числом строк матрицы В. В общем случае 
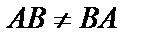, т. е. произведение некоммутативно.
Свойства произведения матриц:
1. 
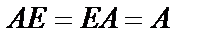(единичная матрица Е – как 1 при умножении чисел);
2. 
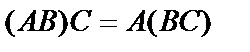– ассоциативно;
3. 
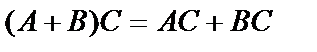дистрибутивный закон.
Пример 1.1.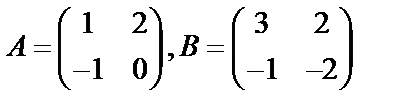 
. Найти 
, 
.
.
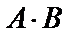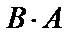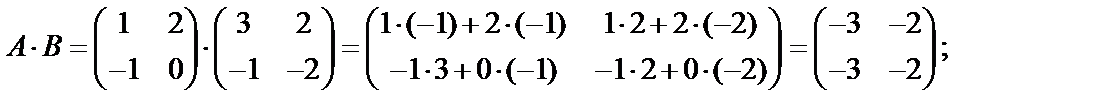
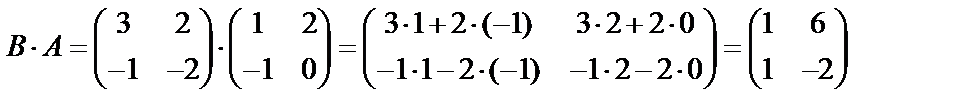Очевидно, что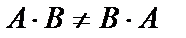 
.
1.3. Определители второго и третьего порядка
Рассмотрим квадратную матрицу порядка n: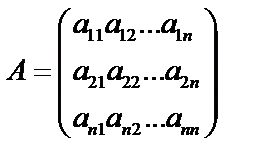 
.
Каждой такой матрице поставим в соответствие определенное число, называемое определителем этой квадратной матрицы. Если порядок равен единице, то матрица состоит из одного числа, и определителем первого порядка назовем величину этого элемента. Если порядок матрицы равен двум, т.е.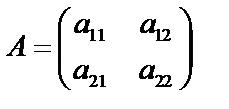 
, то определителем второго порядка назовем число, равное 
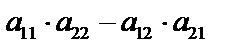и обозначаемое следующим образом: 
.
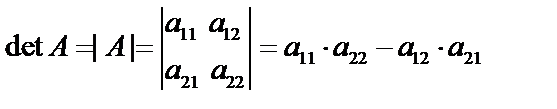Например,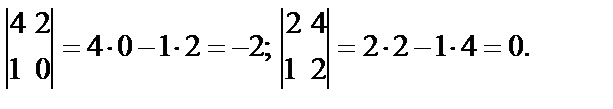 
Определитель второго порядка равен разности произведений элементов главной диагонали и произведения элементов, стоящих на побочной диагонали.
Определителем квадратной матрицы третьего порядка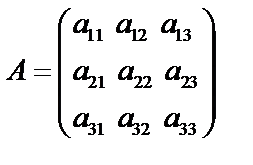 
назовем число, равное: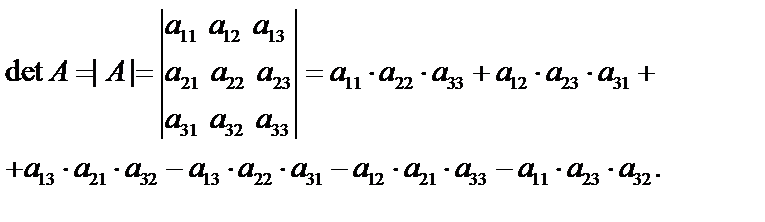 
Например,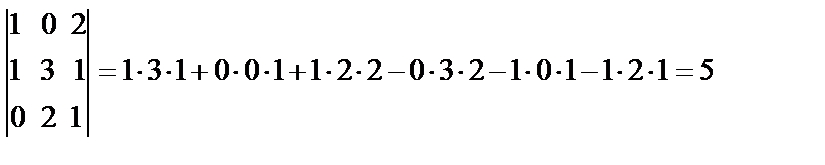 
.
1.4. Основные свойства определителей
Свойства определителей рассмотрим на примере определителей третьего порядка, хотя все свойства справедливы для определителей любого порядка.
1. При транспонировании определителя величина определителя не меняется, т.е.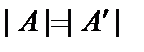 
. Напомним, что транспонирование – замена его строк столбцами. Для доказательства следует расписать определители в правой и левой частях равенства: 
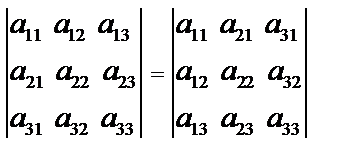. Значит, строки и столбцы в определителе равноправны и если выполняются некоторые свойства для столбцов, то такое же свойство существует и для строк.
2. Если в определителе поменять местами какие-нибудь две строки, то определитель сохраняет свою абсолютную величину, но изменит знак на противоположный.
Например,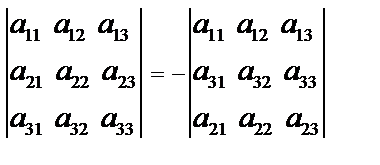 
. Это также доказывается проверкой.
3. Если определитель имеет две одинаковые строки, то он равен нулю.
Пусть |А| =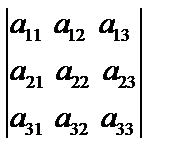 
. Если переставить 2 и 3 строчки, то по свойству «2» получим –|А|, то есть |А| = – |А|, отсюда |А| = 0.
4. Общий множитель, содержащийся во всех элементах строки, можно вынести за знак определителя.
Например,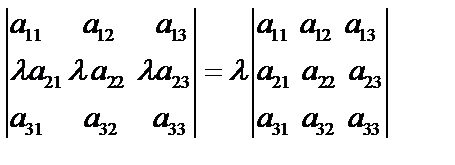 
. Это также доказывается проверкой.
5. Определитель, имеющий нулевую строку (все элементы которой равны нулю), равен нулю.
Для доказательство: в п.4 положим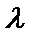 
=0.
6. Если все элементы какой-либо строки состоят из двух слагаемых, то определитель равен сумме двух определителей, в одном из которых элементами этой строки являются первые слагаемые, во втором – вторые, а остальные элементы такие же, как и в данном определителе:
.
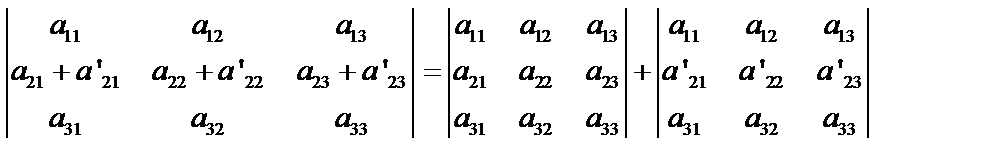Это также доказывается проверкой.
7. Определитель не изменится, если к элементам какой-либо строки прибавить соответствующие элементы другой строки, умноженные на любое число.
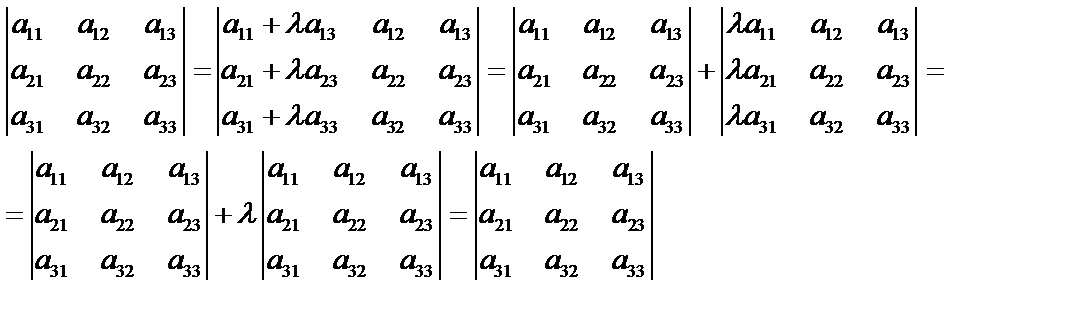т. к. второй определитель равен нулю.
Следствие: определитель равен нулю, если элементы каких-либо двух его строк пропорциональны.
Свойство 7 можно обобщить: если элементы какого-либо столбца определителя является линейной комбинацией других его столбцов, то определитель равен нулю. Если столбцы определителя линейно зависимы, то определитель равен нулю.
1.5. Алгебраические дополнения
Минором любого элемента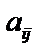 
матрицы n -го порядка будем называть определитель порядка 
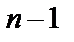, соответствующий матрице, которая получена из данной вычеркиванием строчки с номером i и столбца с номером j, на пересечении которых находится данный элемент. Минор элемента 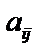будем обозначать 
.
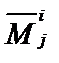Алгебраическим дополнением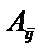 
элемента 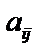назовем число, равное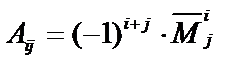 
Тогда сформулируем свойство 8 определителей:
8. Определитель равен сумме произведений элементов какой-нибудь строки (или столбца) на алгебраические дополнения этих элементов.
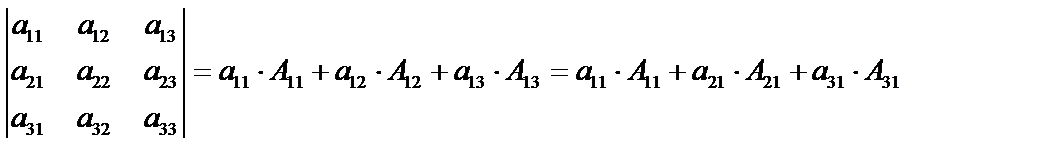
Последнее свойство определителей:
9. Сумма произведений элементов какой-либо строки на соответствующие алгебраические дополнения элементов другой строки равна нулю.
1.6. Ранг матрицы
Пусть имеется прямоугольная матрица размером m на n: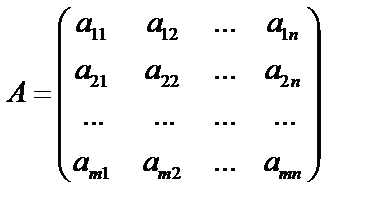 
. Если в этой матрице выделить k строк и k столбцов, то мы получим квадратную матрицу порядка k. Определитель этой матрицы называется минором k – го порядка матрицы А. Среди этих миноров найдется хотя бы один, отличный от нуля, минор старшего порядка. Порядок наибольшего минора, отличного от нуля, называется рангом матрицы r ( A ). Тот минор r-го порядка, который отличен от нуля, назовем базисным минором (у матрицы А может быть несколько миноров r-го порядка, которые отличены от нуля). Строки и столбцы, на пересечении которых стоит базисный минор, назовем соответственно базисными строками и базисными столбцами.
Свойства ранга:
1. Ранг матрицы не меняется при ее транспонировании, т.к. строки и столбцы равноправны в отношении ранга.
2. Ранг матрицы не меняется при перестановке ее строк.
3. Ранг матрицы не меняется при умножении всех элементов какой-либо строки на отличное от нуля число.
4. Ранг матрицы не меняется, если к одной из ее строк прибавить другую строку, умноженную на некоторое число.
5. Ранг матрицы не меняется, если удалить нулевую строку.
6. Ранг матрицы не меняется, если удалить строку, являющейся линейной комбинацией другой строки.
Напомним, что элементарными называются следующие преобразования матриц:
Перестановка двух любых строк и столбцов;
Умножение строки или столбца на число отличное от нуля;
Прибавление к одному столбцу или строке линейной комбинации других столбцов или строк.
Элементарное преобразование не меняет ранг матрицы (это следует из свойств).
Канонической называется матрица, у которой в начале главной диагонали стоит подряд несколько единиц, а все остальные элементы равны нулю.
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической.
Ранг канонической матрицы равен числу единиц на ее главной диагонали.
Рассмотрим другой метод вычисления ранга матрицы, называемый методом окаймляющих миноров. В рассматриваемой матрице находим элемент, отличный от нуля, тогда ранг матрицы не меньше единицы. Затем выбираем минор второго порядка (определитель), отличный от нуля и содержащий выбранный ранее элемент. Если такой минор существует, то ранг матрицы не менее двух. Далее выбираем минор 3-его порядка, отличный от нуля, в который входит минор второго порядка. Если такой минор 3-его порядка существует, то ранг матрицы не менее трех, и т.д.
1.7. Обратная матрица
Рассмотрим квадратную матрицу А порядка n: 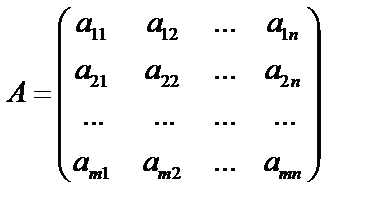. Считаем, что матрица А – невырожденная, т.е. ее определитель отличен от нуля.
Квадратная матрица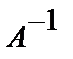 
называется обратной для матрицы А, если выполняются равенства:
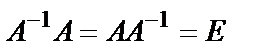, где Е – единичная матрица порядка n.
Теорема. Для того чтобы квадратная матрица А имела обратную матрицу, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
Получим формулу для обратной матрицы: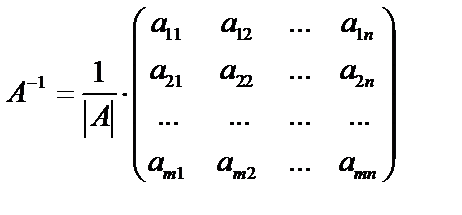 
.
Пример 1.2. Вычислить обратную матрицу для матрицы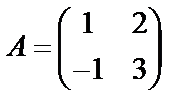 
Определитель матрицы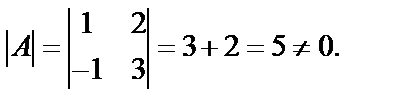 
Алгебраические дополнения: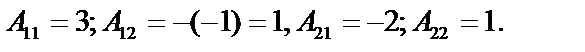 
Тогда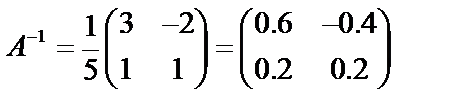 
.
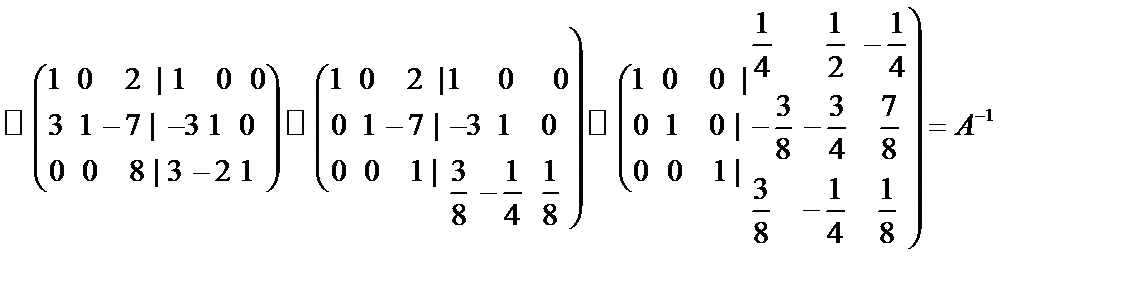
Пример 1.3. Вычислить обратную матрицу для матрицы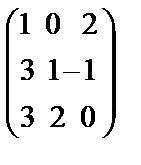 
.
1) 
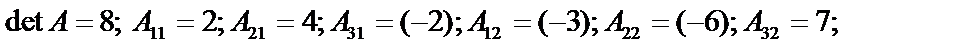
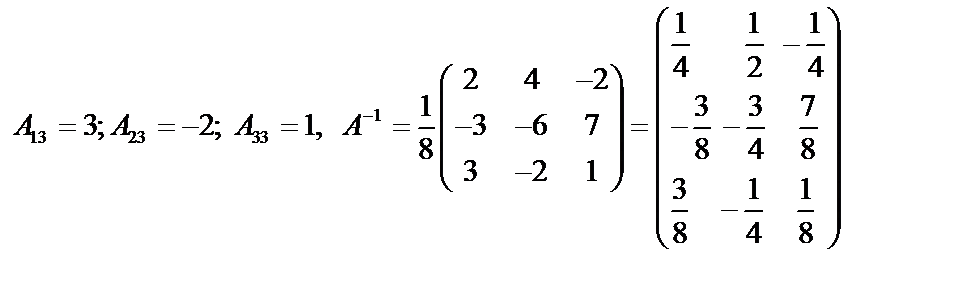
2) 
