Жидкость с Вязкостью. Математические преобразования эквивалентно трансформируют уравнения Навье-Стокса
7. Жидкость с Вязкостью, Когда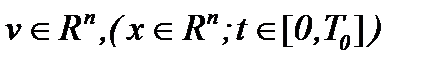 
В этом параграфе покажем, что определенные математические преобразования эквивалентно трансформируют уравнения Навье-Стокса в линейные уравнения в случае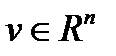 
. Тем самым, удостоверившись, что решения в строго аналитической форме или решения, основанные на методе Пикара, имеют место не только для 3D уравнений Навье-Стокса с вязкостью [1], докажем, что и для nD уравнений Навье-Стокса имеют аналогичные решения в 
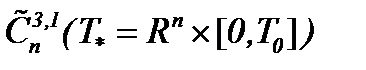или 
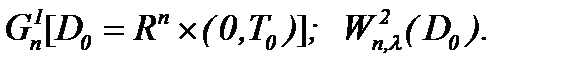
Предложенные в параграфе 4 методы интегральных преобразований были основаны на интегралах вольтерровского типа по переменной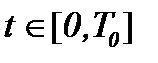 
, когда 
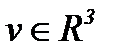. Эти методы были введены так, чтобы превратить нелинейную задачу Навье-Стокса в линейную задачу теплопроводности с условием Коши. Наша цель заключается в развитии указанных методов для уравнений Навье-Стокса в многомерном случае, а именно 
:
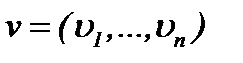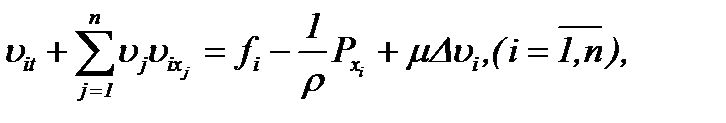(1.1)n
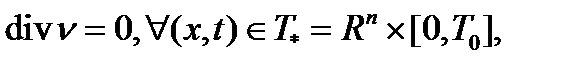(1.2)n
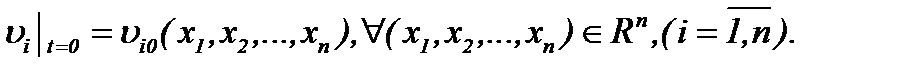(1.3)n
При условиях (1.2)n и (1.3)n система Навье-Стокса (1.1)n может иметь или аналитическое гладкое и единственное решение в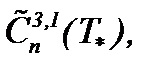 
или условно-гладкое единственное решение в 
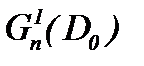, в чем убедимся на самом деле.
7.1. Жидкость с вязкостью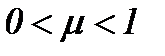 
, когда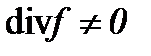 
Пусть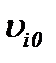 
начальные компоненты вектора скорости 
в момент времени 
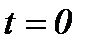определяются, согласно (1.3)n, следующим образом
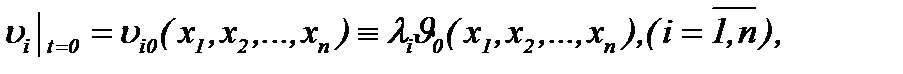(7.1)
где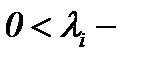 
известные константы. Поэтому относительно компоненты скорости 
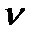можем ввести формулу
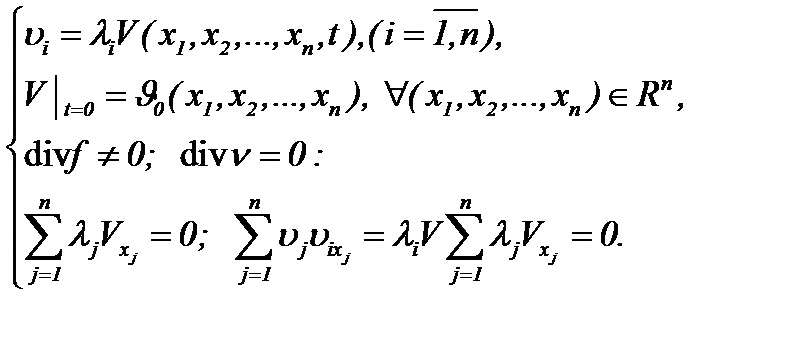(7.2)
Тогда замена (7.2) эквивалентно превратит уравнения (1.1)n в систему линейных неоднородных уравнений вида
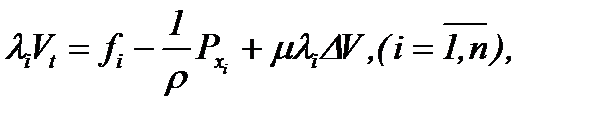(7.3)
где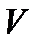 
новая неизвестная функция, которая определяет решение задачи Навье-Стокса на основе формулы (7.2). Чтобы решить систему (7.3), в первую очередь, найдем давление 
.
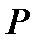Действительно, применяя АПС, из системы (7.3) имеем
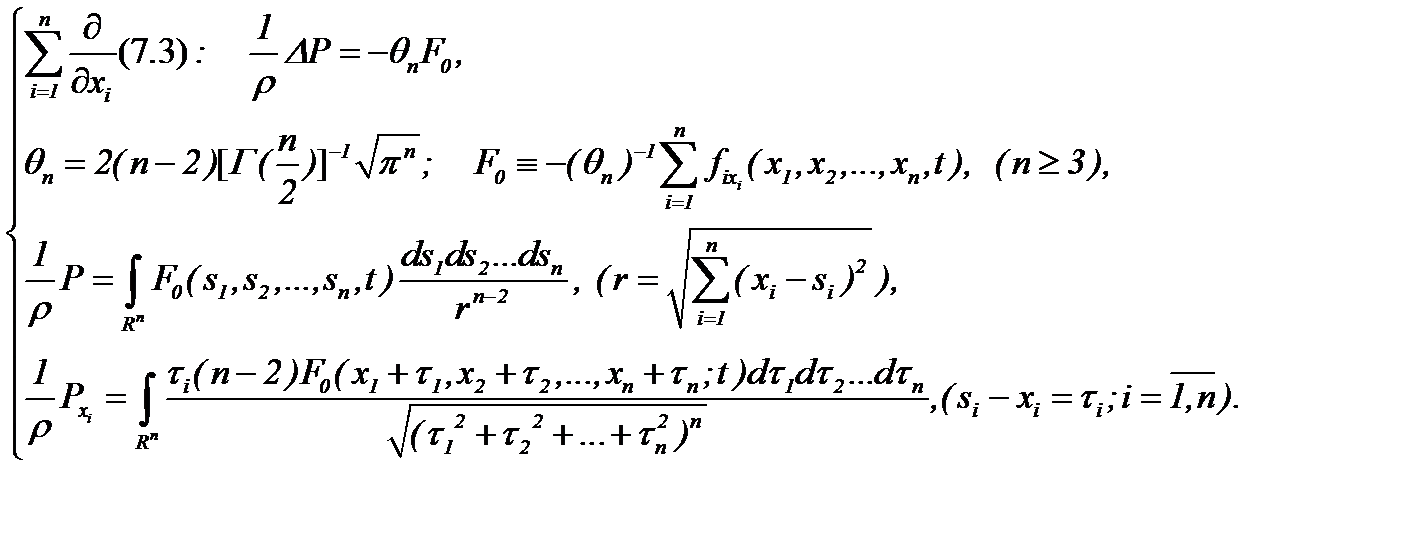(7.4)
Следовательно, получили
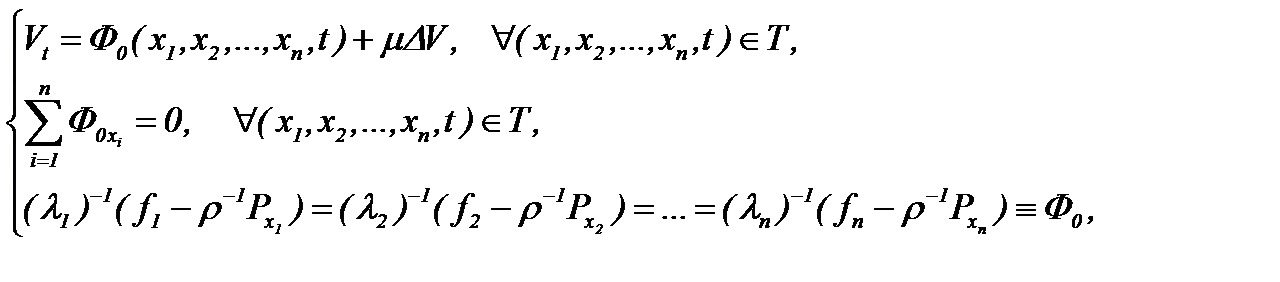(7.5)
а это означает, что система (7.3) преобразована в линейное уравнение теплопроводности с условием Коши вида (7.5), которая разрешима в классе функций с достаточно гладкими начальными данными,
а потому существует условно-гладкое и единственное решение задачи Навье-Стокса в 
Действительно, из системы (7.5) следует
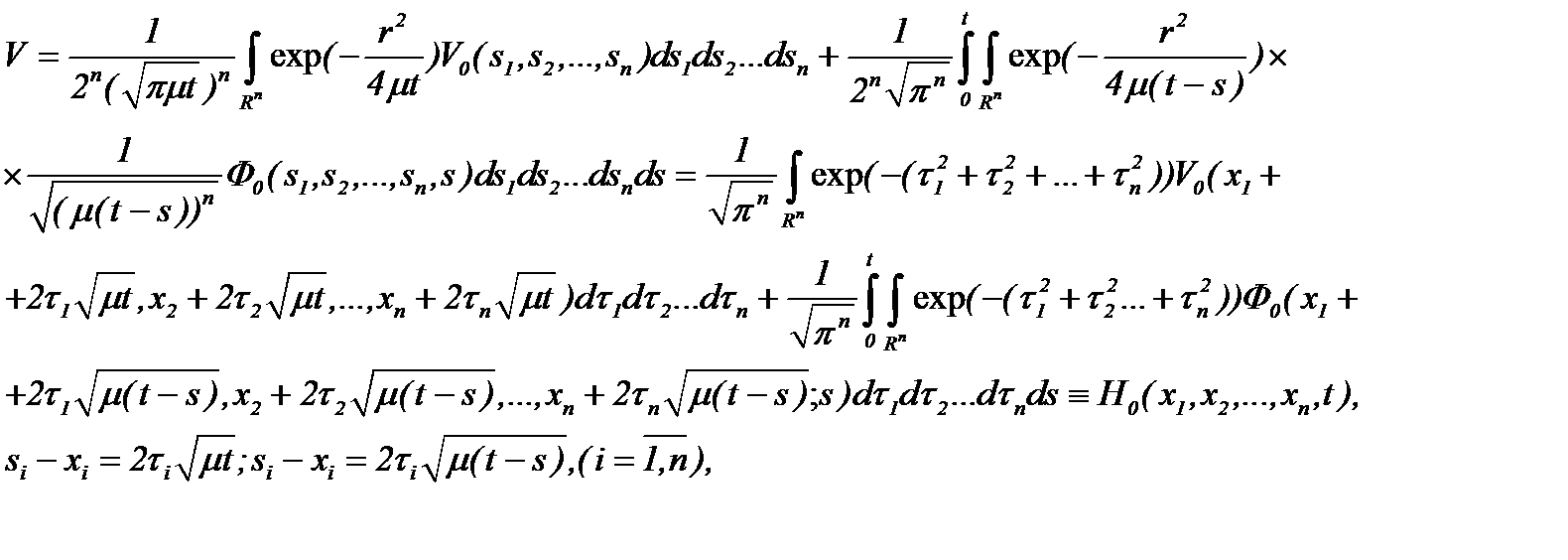(7.6)
где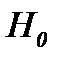 
– известная функция. Для доказательства ограниченности решения (7.5) в 
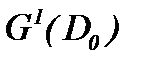, как видно, решение (7.5) сведено к виду (7.6), когда
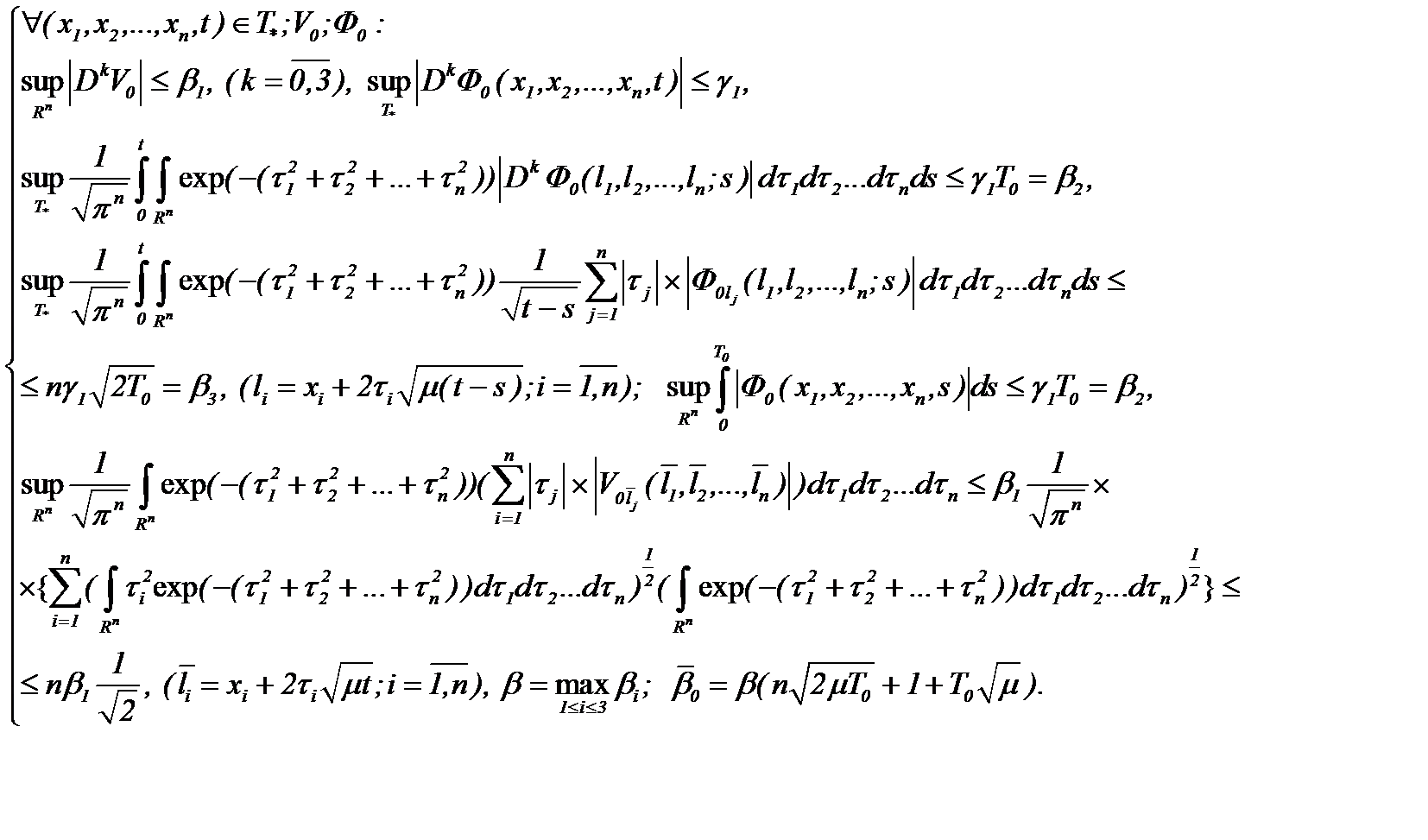(7.7)
Теперь, оценивая (7.6) при соблюдении условия (7.7) в 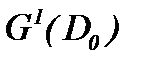, имеем
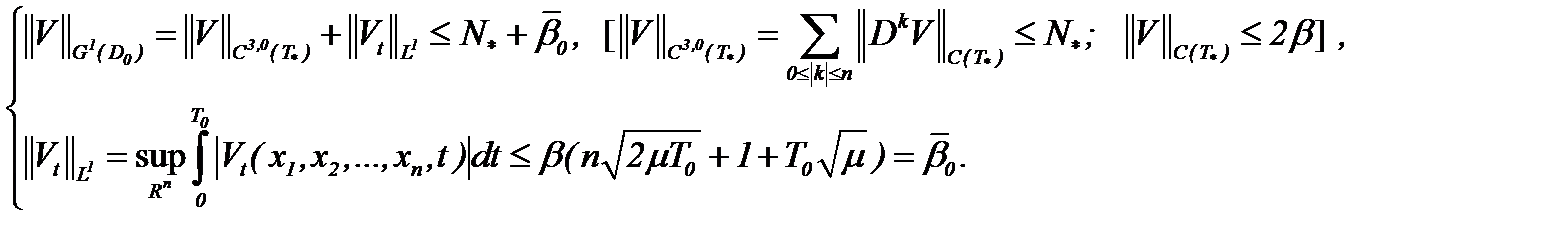(7.8)
Единственность (7.6) в 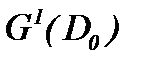очевидна на основе метода от противного. Результаты (7.6) с
условием (7.2), (7.7) получены, когда гладкость функций требуется только по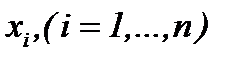 
, а производная первого порядка по времени определяется для всех 
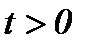. Следовательно, на основе преобразования (7.2) получаем решения системы (1.1)n, которые удовлетворяют условию (1.2)n, т.е.
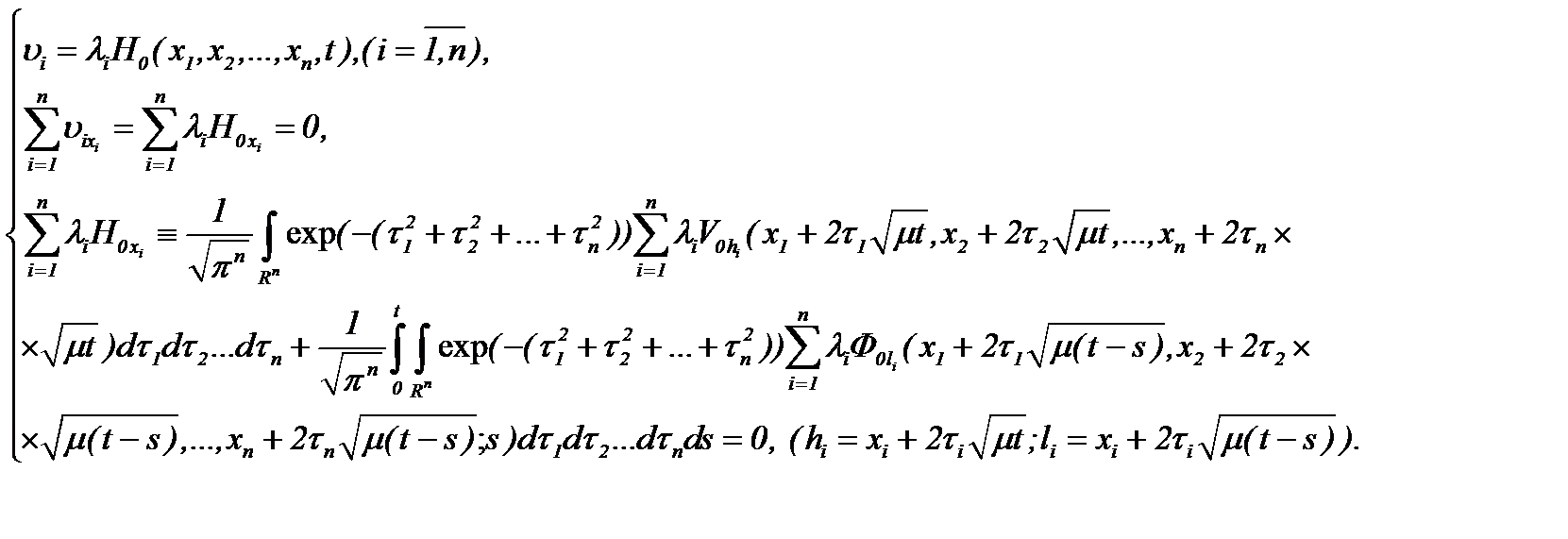(7.9)
Наконец, с учетом нормы пространства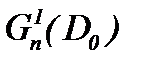 
получим оценку решения (7.9):
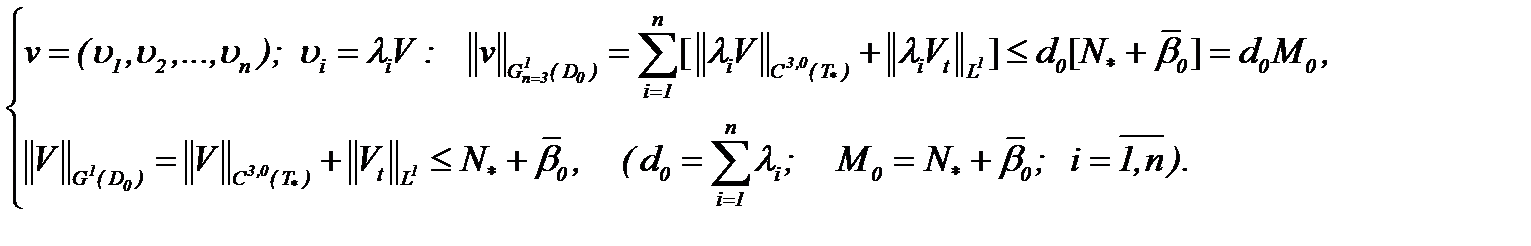(7.10)
Следовательно, полученные результаты формулируются следующей теоремой.
Теорема 8. Задача (1.1)n, (1.2)n, (7.1) при условиях (1.2)n, (7.1), (7.7) и (7.10) имеет единственное решение в 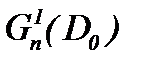, которое определяется правилом (7.9).
Замечание 7. Известно, что турбулентное решение обладает свойством условной гладкости в аналитическом смысле [4]. Поэтому, полагаем, что класс подходящих решений задачи Навье-Стокса является весовое пространство типа Соболева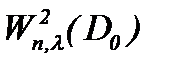 
. Так как 
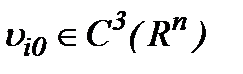, то решение (7.6) задачи Навье-Стокса (1.1)n – (1.3)n принадлежит 
:
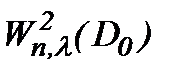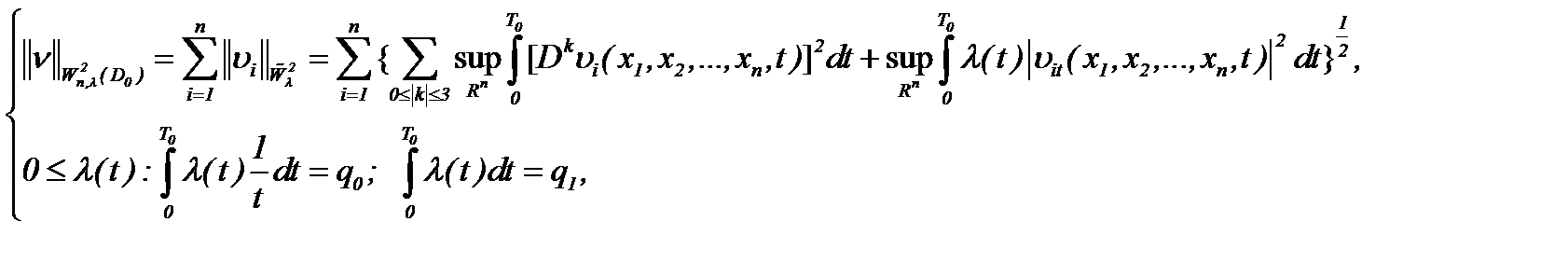
если имеет место
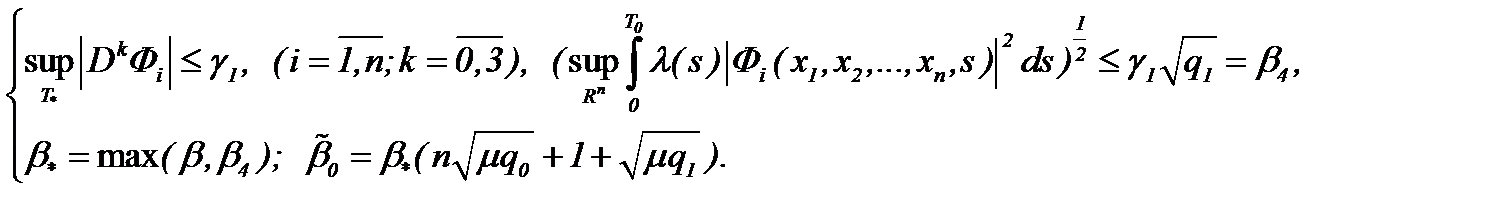(7.11)
Для этого достаточно показать, что функция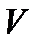 
является элементом пространства 
:
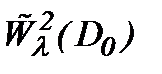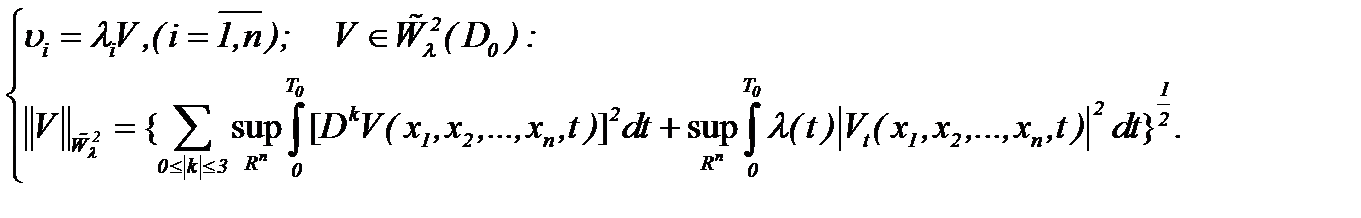
Пусть решение системы (7.5) представлено в виде (7.6) с условиями (7.7), (7.13). Тогда, проведя оценки (7.6) в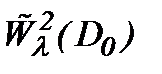 
, получим
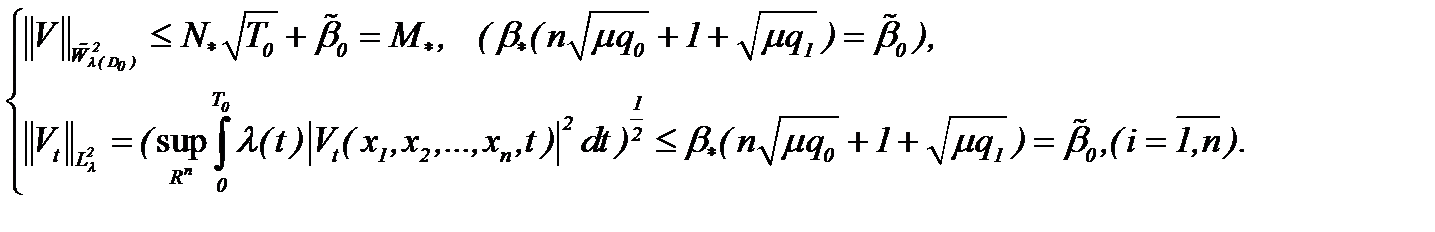(7.12)
Значит, на основании (7.12), оценивая (7.2) в смысле нормы пространства 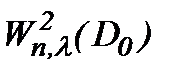, имеем
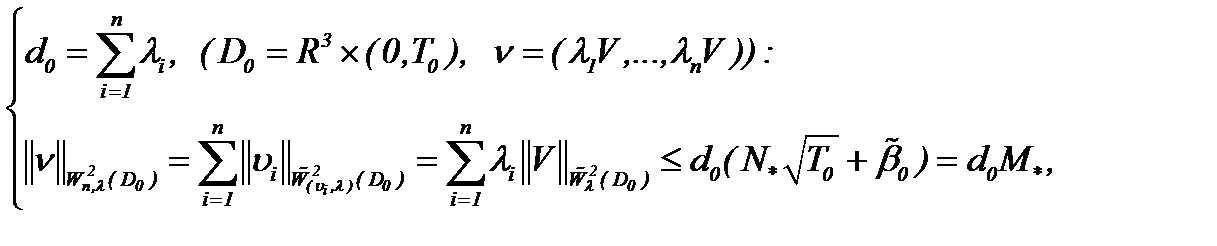
а это означает, что задача (1.1)n – (1.3)n при условиях (1.2)n, (1.3)n, (7.1), (7.7) и (7.11) имеет строгое и условно-гладкое решение в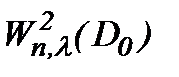 
, что и требовалось доказать.
7.2. Жидкость с вязкостью 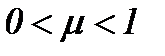, когда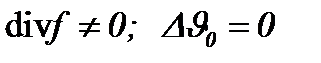 
I . Целью пункта является модификация метода (7.2), необходимая, чтобы получить аналитическое решение задачи Навье-Стокса с вязкостью, принадлежащее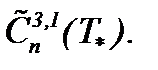 
Поскольку имеем
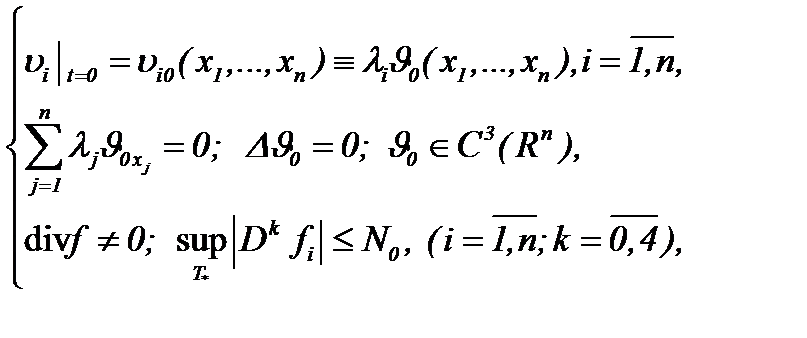(7.13)
то применим преобразование
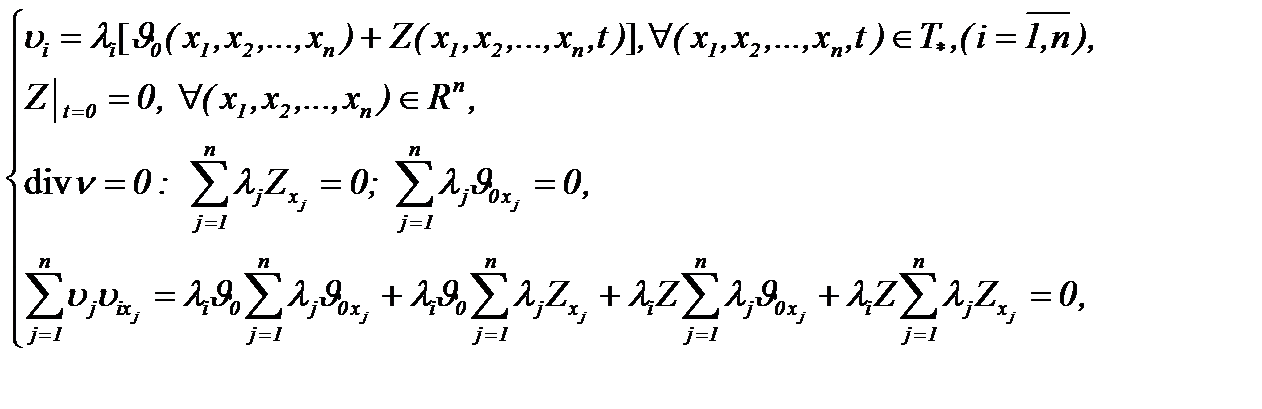(7.14)
где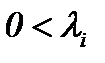 
– известные константы. Тогда система (1.1)n трансформируется к виду
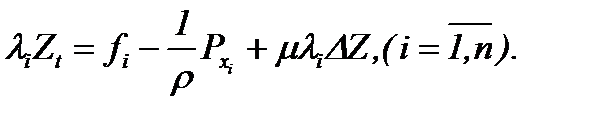(7.15)
Из системы (7.15), учитывая условия (7.13), (7.14) и применяя АПС, получим уравнение (7.4).
Таким образом, на основе (7.4) вместо уравнения (7.15) имеем линейное неоднородное дифференциальное уравнение с условием Коши
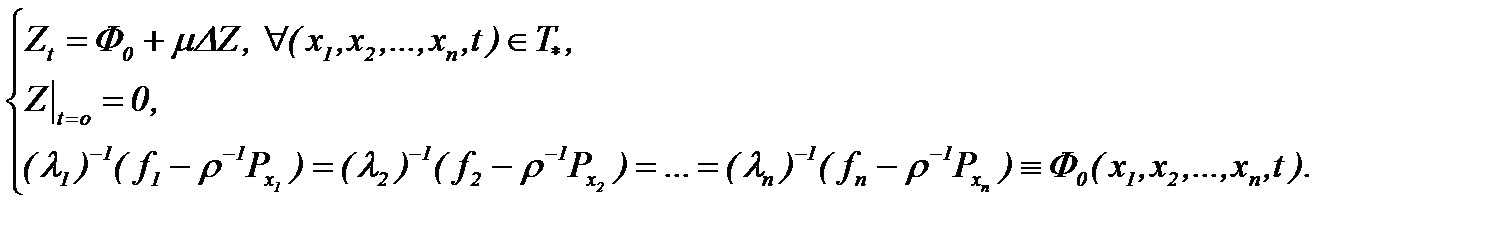(7.16)
Тогда решение задачи (7.16) представимо в виде
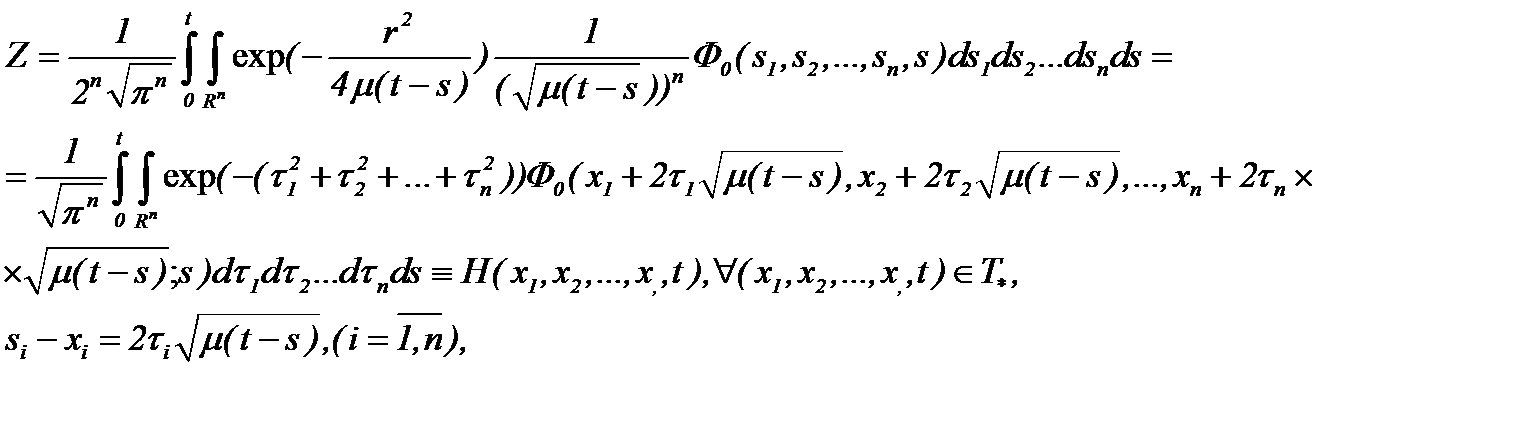(7.17)
где H – известная функция. Найденное решение (7.17) удовлетворяет уравнению (7.16).
Действительно, рассчитав частные производные системы (7.17)
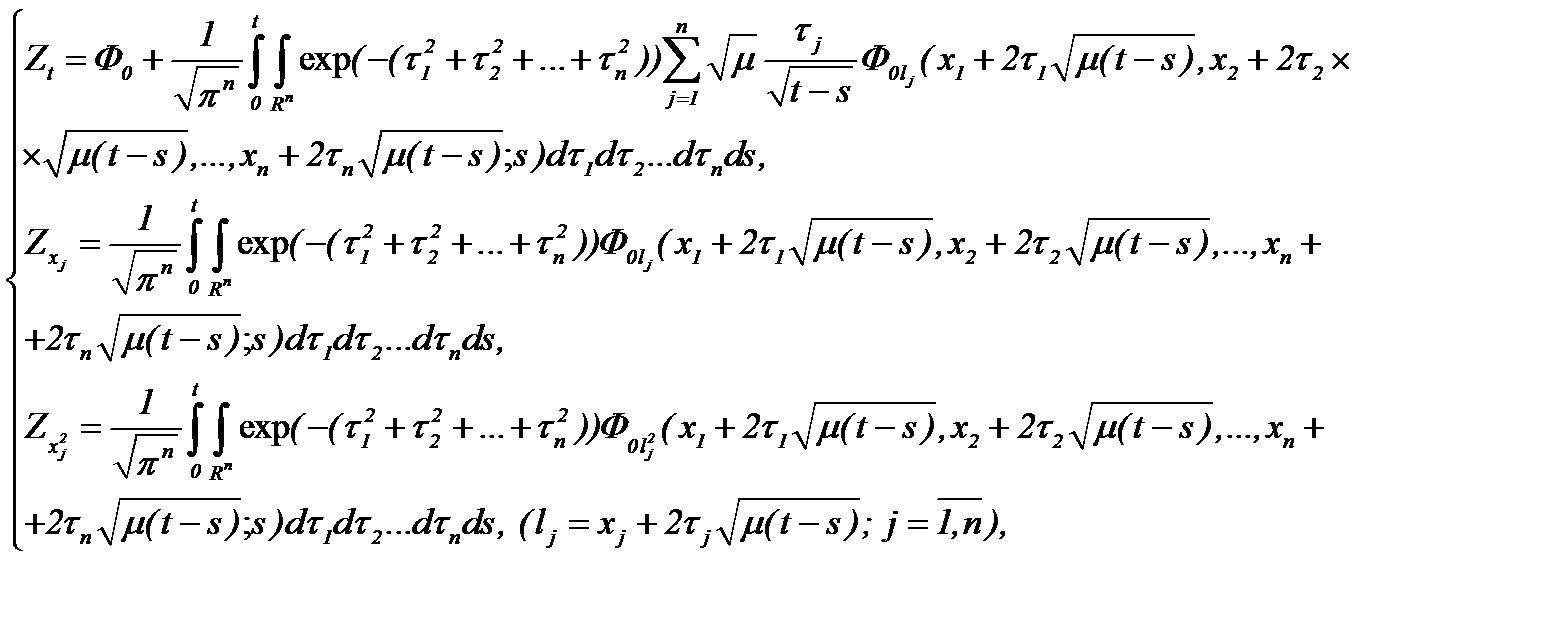(7.18)
а, затем, подставляя (7.18) в (7.16), имеем
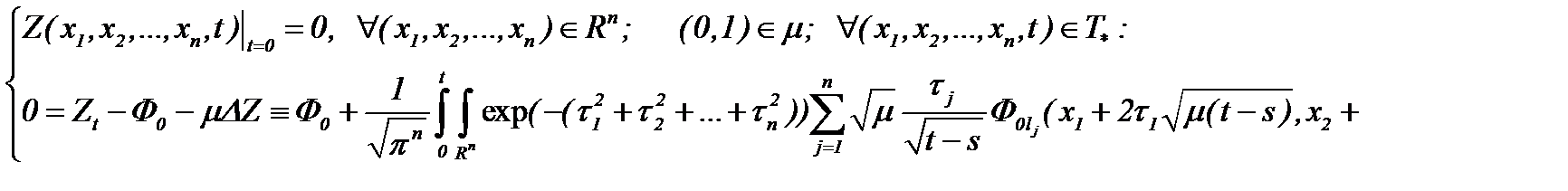
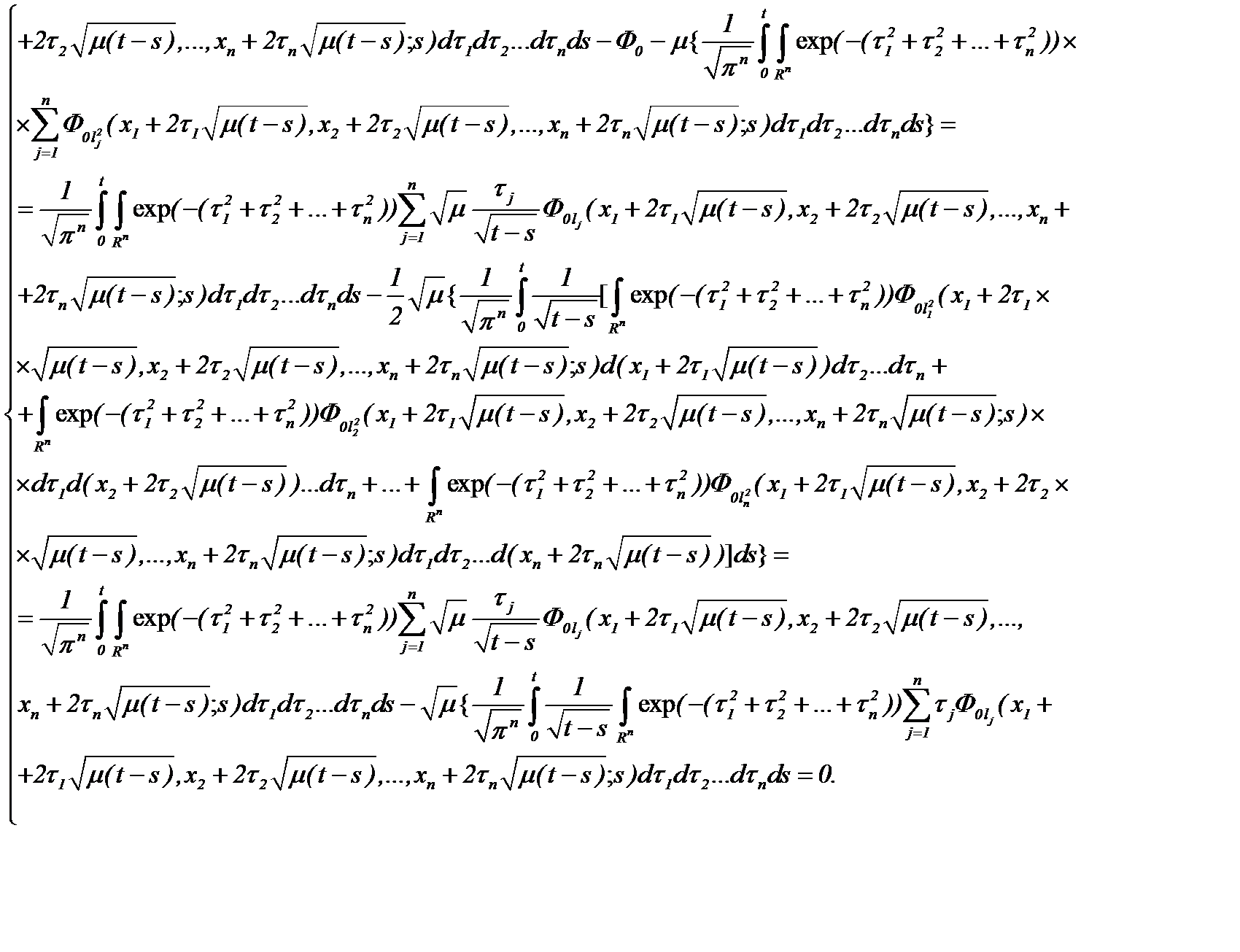
Таким образом, получено то, что и требовалось доказать.
Из полученных результатов следует, что функции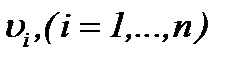 
определяются на основе (7.14), а именно
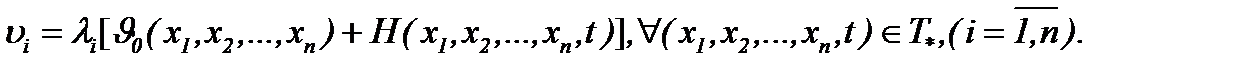(7.19)
Кроме того, учитывая частные производные систем первого порядка (7.19), принимая во внимание (1.2)n и (7.14), а, затем, подводя итог, получим, что система (7.19) удовлетворяет условию (1.2)n:
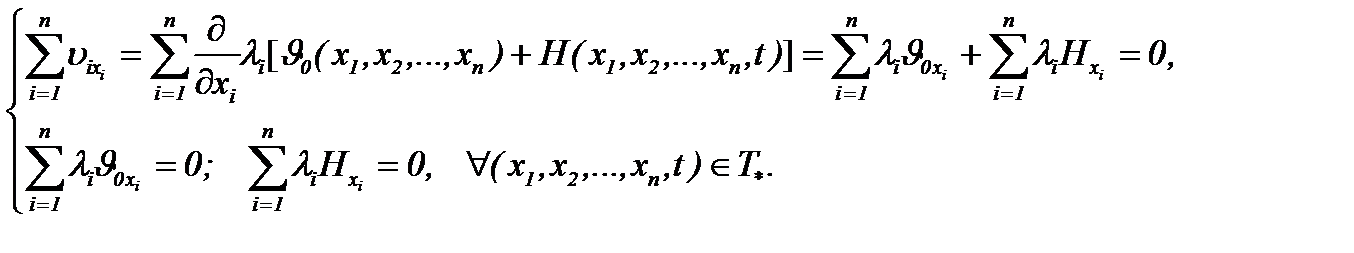
II . Так как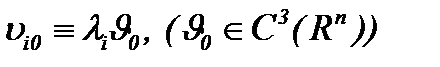 
, то решение задачи (1.1)n – (1.3)n ограничено в 
:
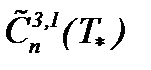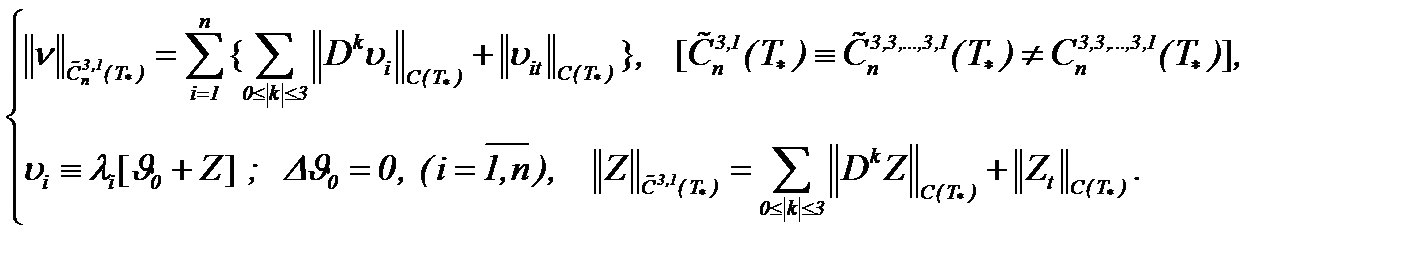
Действительно, если
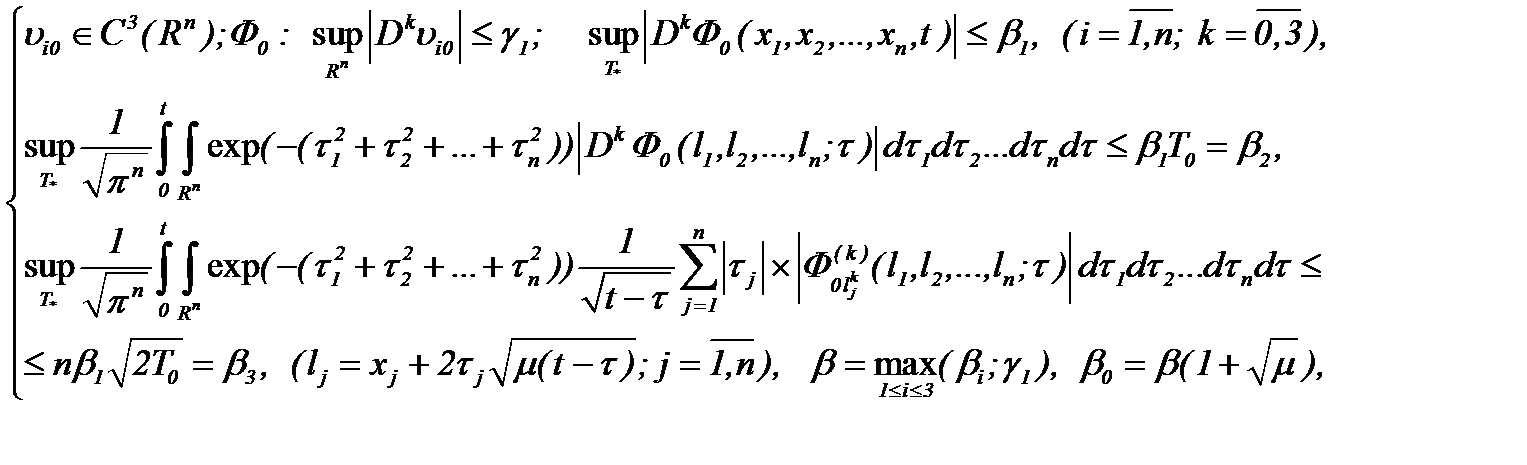(7.20)
то на основе (7.17) получим
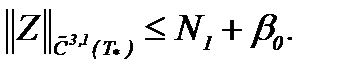
Наконец, оценивая (7.19) в смысле нормы пространства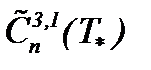 
, имеем
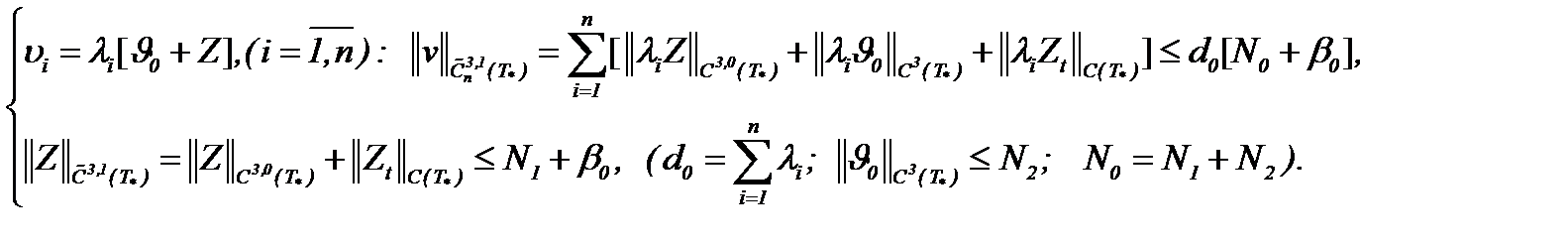
Лемма 3. При условиях (1.2)n, (7.13), (7.14) и (7.20) уравнение (7.17) имеет единственное решение в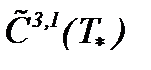 
.
Теорема 8*. Задача (1.1)n, (1.2)n, (7.13) при выполнении условий леммы 3 разрешима в 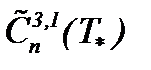и решение определяется правилом (7.19).
Итогом исследований настоящего пункта являются результаты теоремы 8*, на основании которых решение системы (1.1)n является строго аналитическим и единственным решением задачи (1.1)n – (1.3)n в 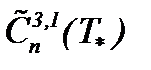. Поэтому корректность постановки задачи (1.1)n – (1.3)n разрешается, исходя из результатов теоремы 8*.