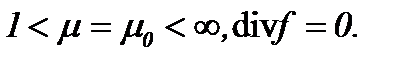Жидкость со средней и большой вязкостью
5.3. Жидкость со средней и большой вязкостью, когда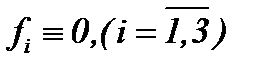 
В 5.1 и 5.2 изучена жидкость со средней вязкостью, если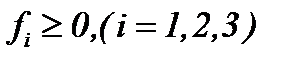 
. Здесь рассмотрим метод интегрирования уравнений Навье-Стокса (1.1) со средним и небольшим числом Рейнольдса ( 
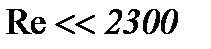) для уравнений [12], содержащих все инерционные
члены и условие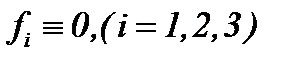 
. Цель этого пункта: найти для метода (5.22) такую модификацию, чтобы получить аналитическое решение задачи Коши для однородных уравнений Навье-Стокса в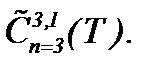 
В этой связи, здесь исследуем задачу
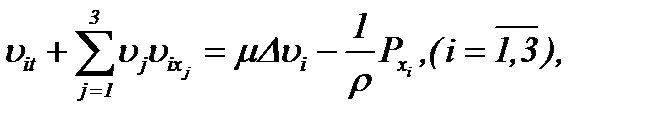(5.31)
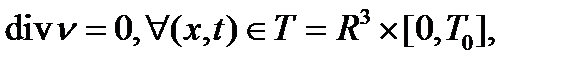(5.32)
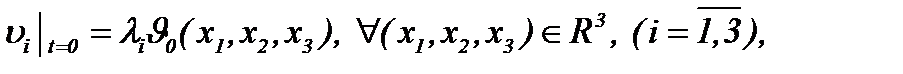(5.33)
где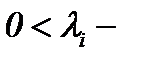 
известные константы и
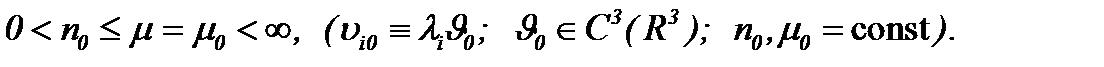(5.34)
Чтобы достичь поставленной цели, будем считать, что существуют функции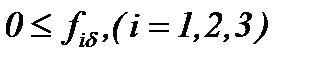 
, которые удовлетворяют условиям
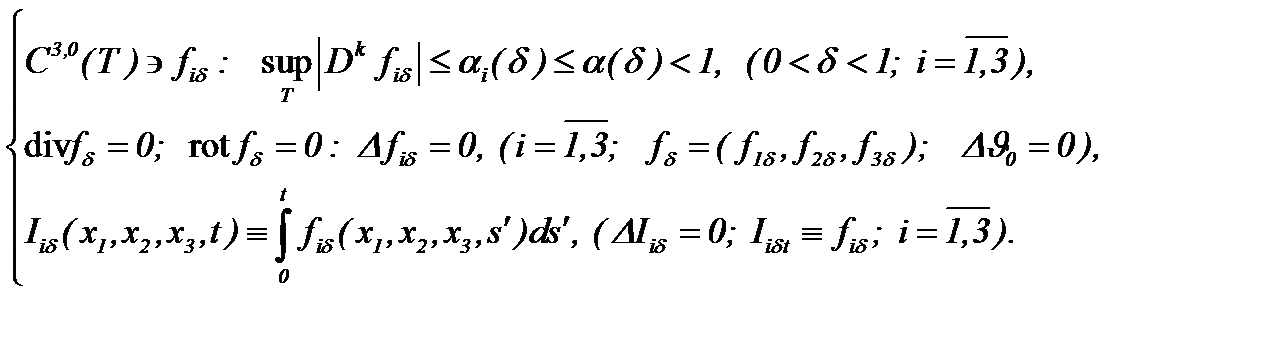(5.35)
Тогда применим метод
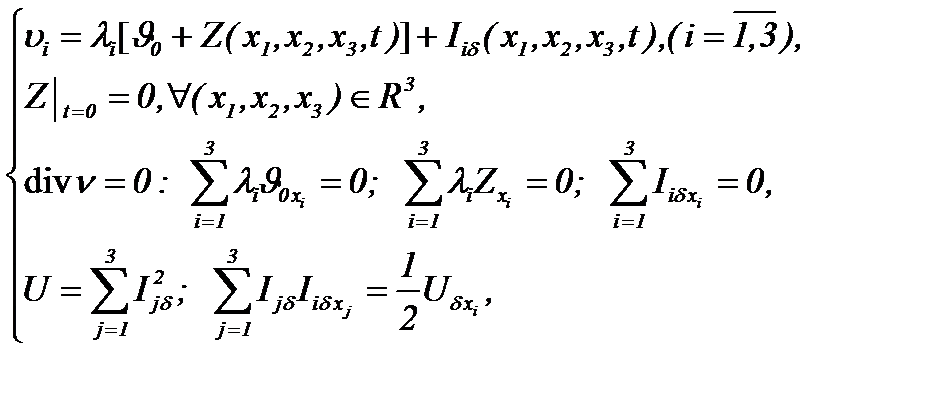(5.36)
для которого соблюдаются условия
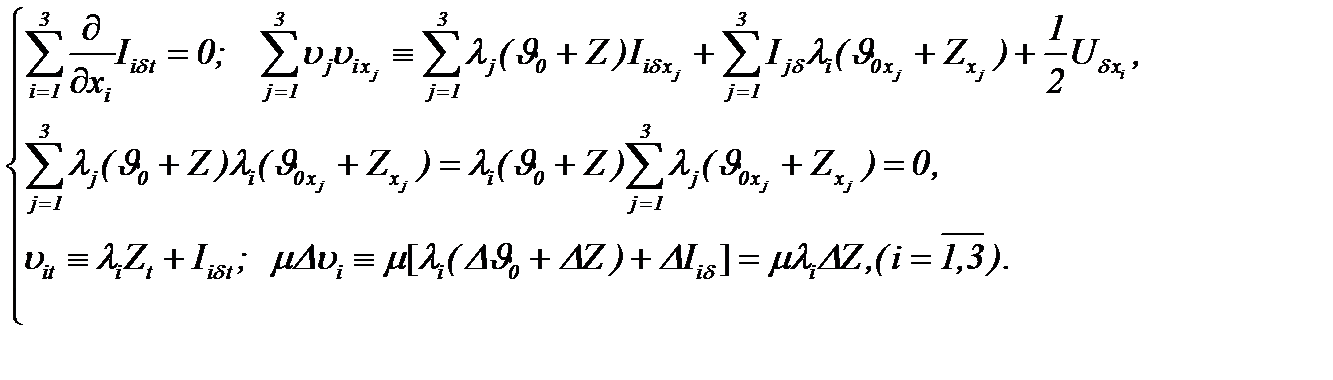(5.37)
С помощью преобразования (5.36) при выполнении условий (5.32) – (5.35) и (5.37), так как все инерционные члены линеаризуется на основе функций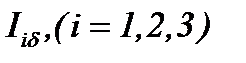 
, уравнение
Навье-Стокса с трением (5.31) сводится к неоднородным линейным уравнениям
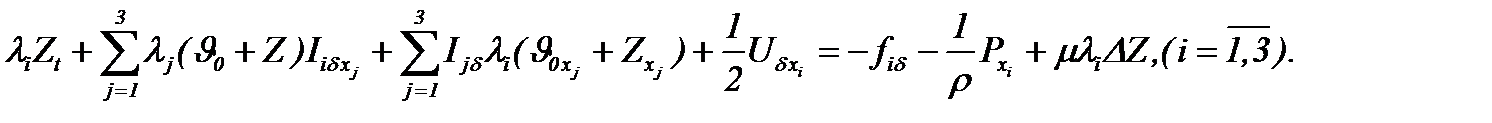(5.38)
Из системы (5.38) с учетом условий (5.31) – (5.33), применяя алгоритм АПС, получим уравнение:
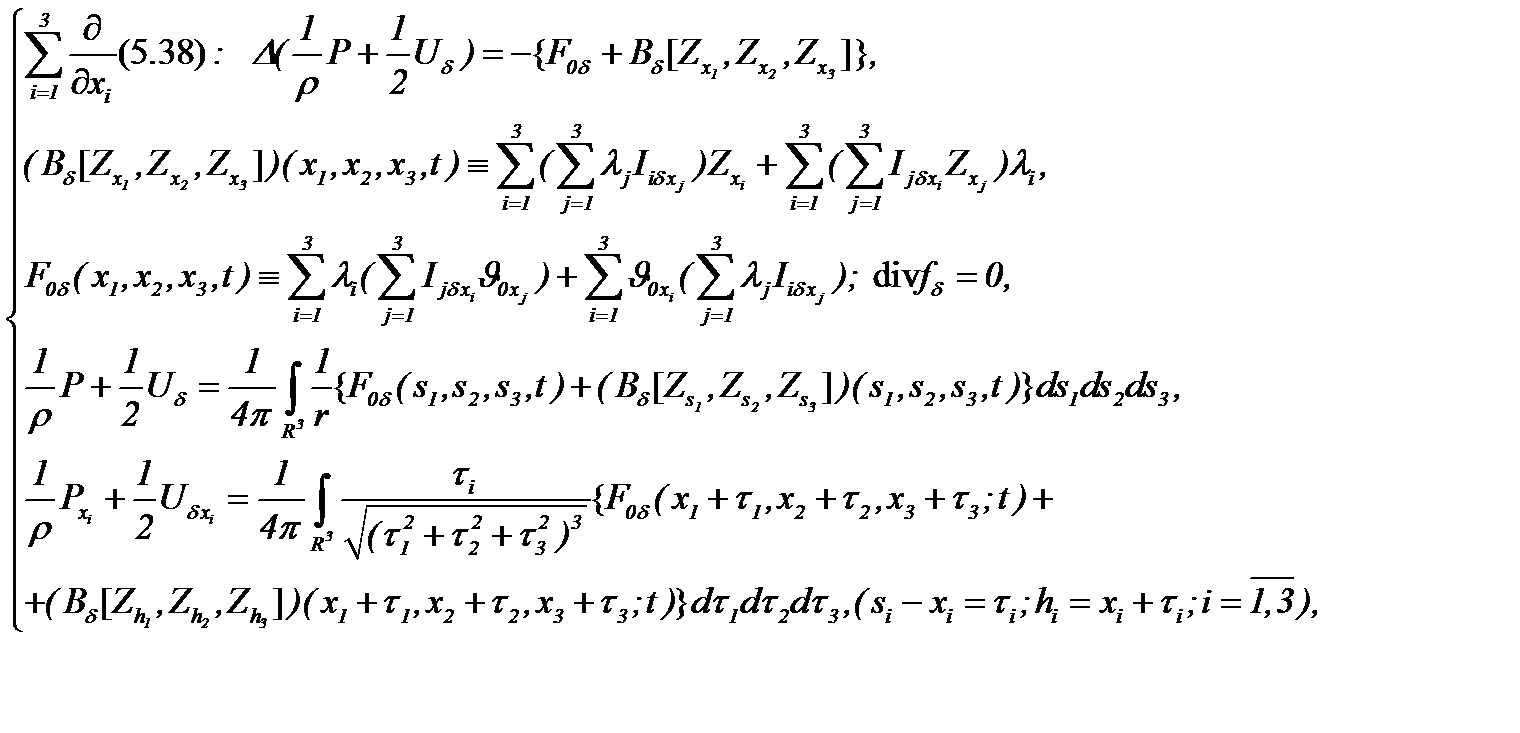(5.39)
так как имеет место
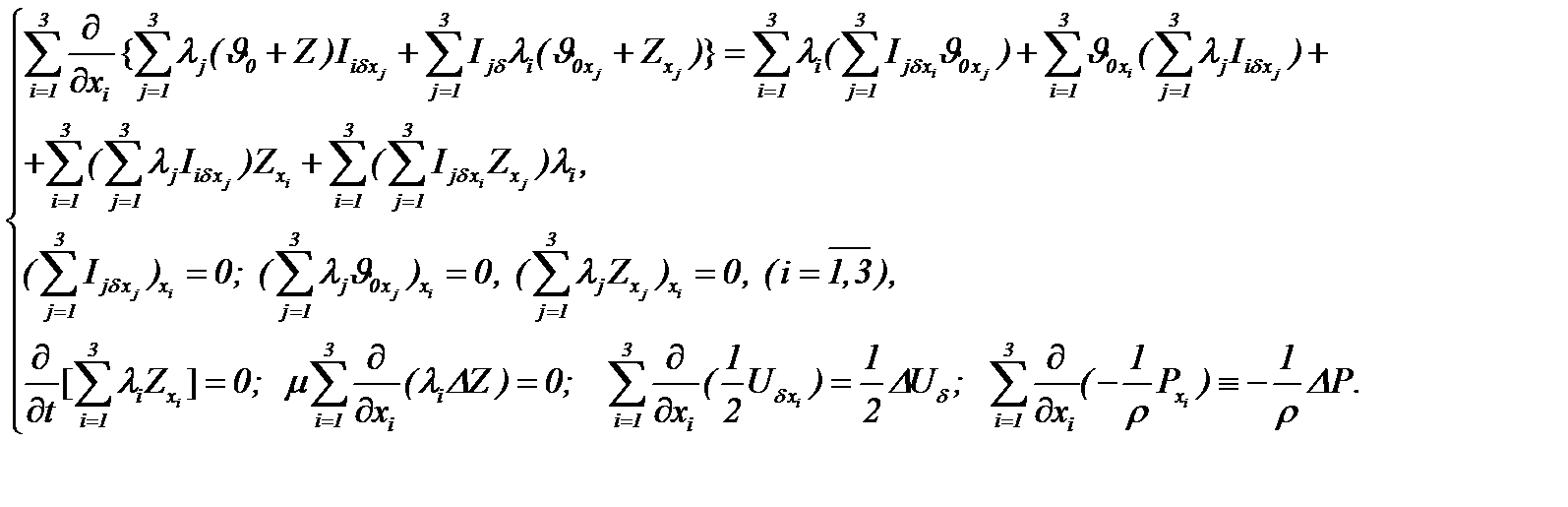
Тогда на основании (5.39) система (5.38) эквивалентно преобразуется к виду
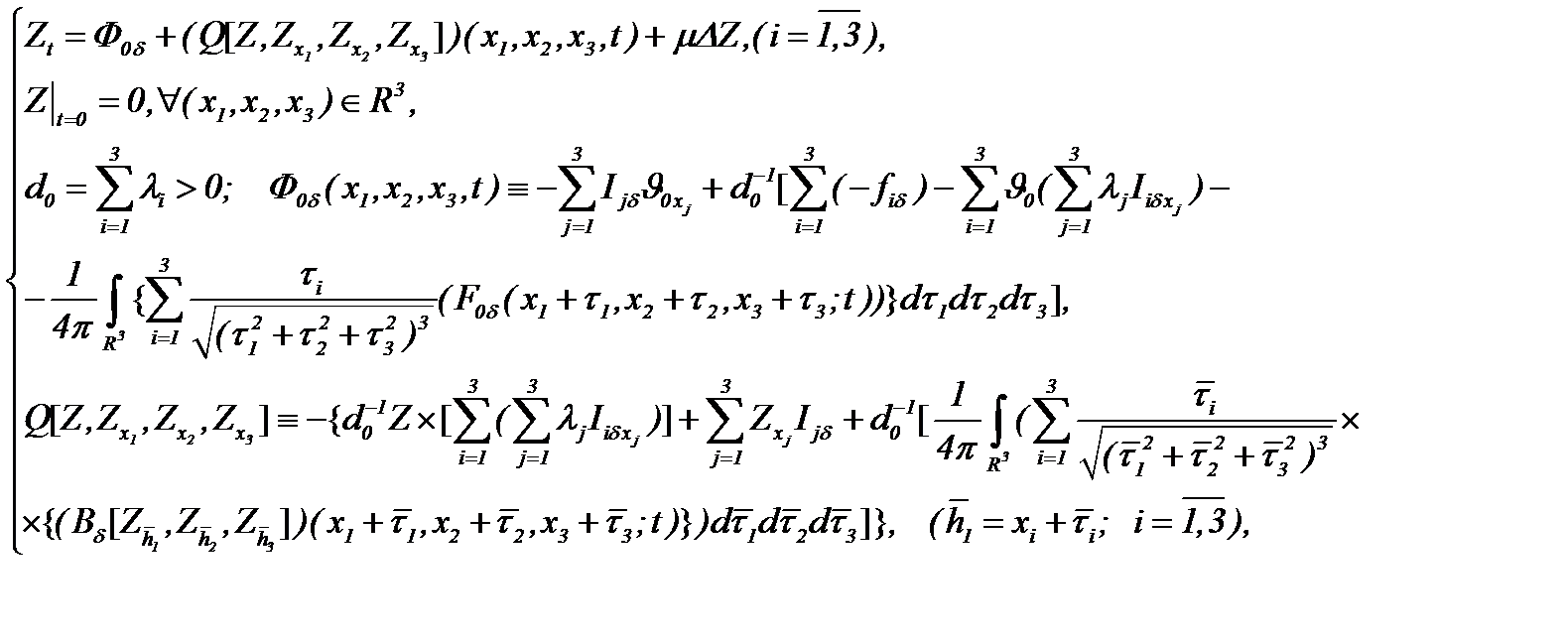(5.40)
для которого имеем
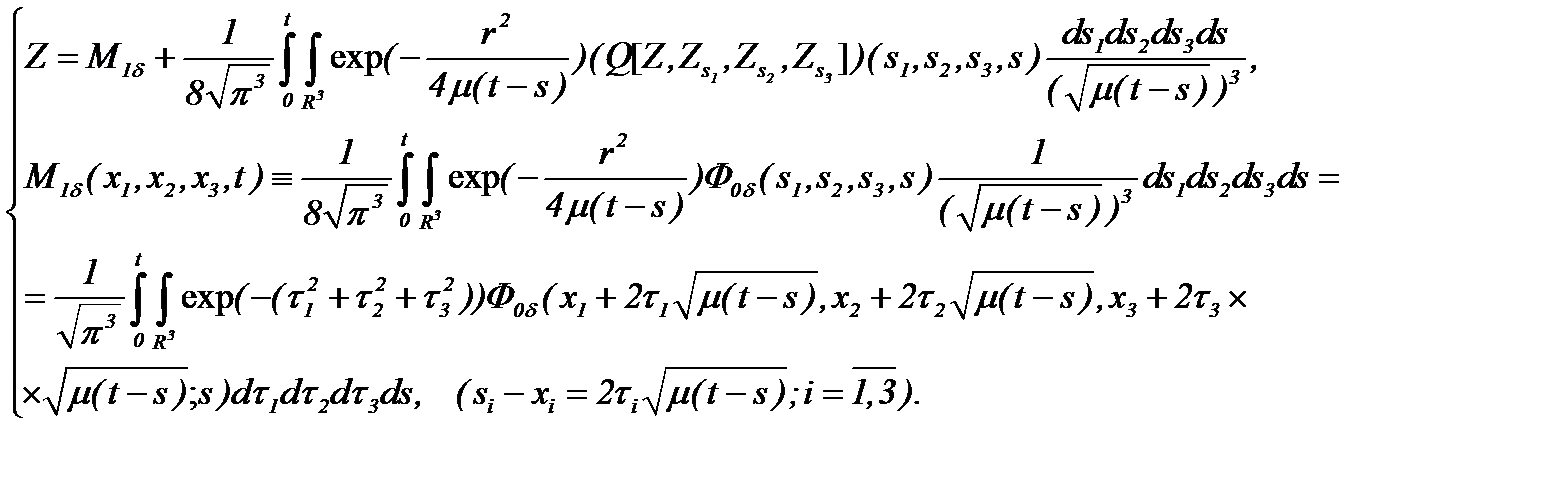(5.41)
Чтобы доопределить (5.41), вычислим частные производные по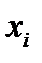 
и на основе математических преобразований выведем систему интегральных уравнений
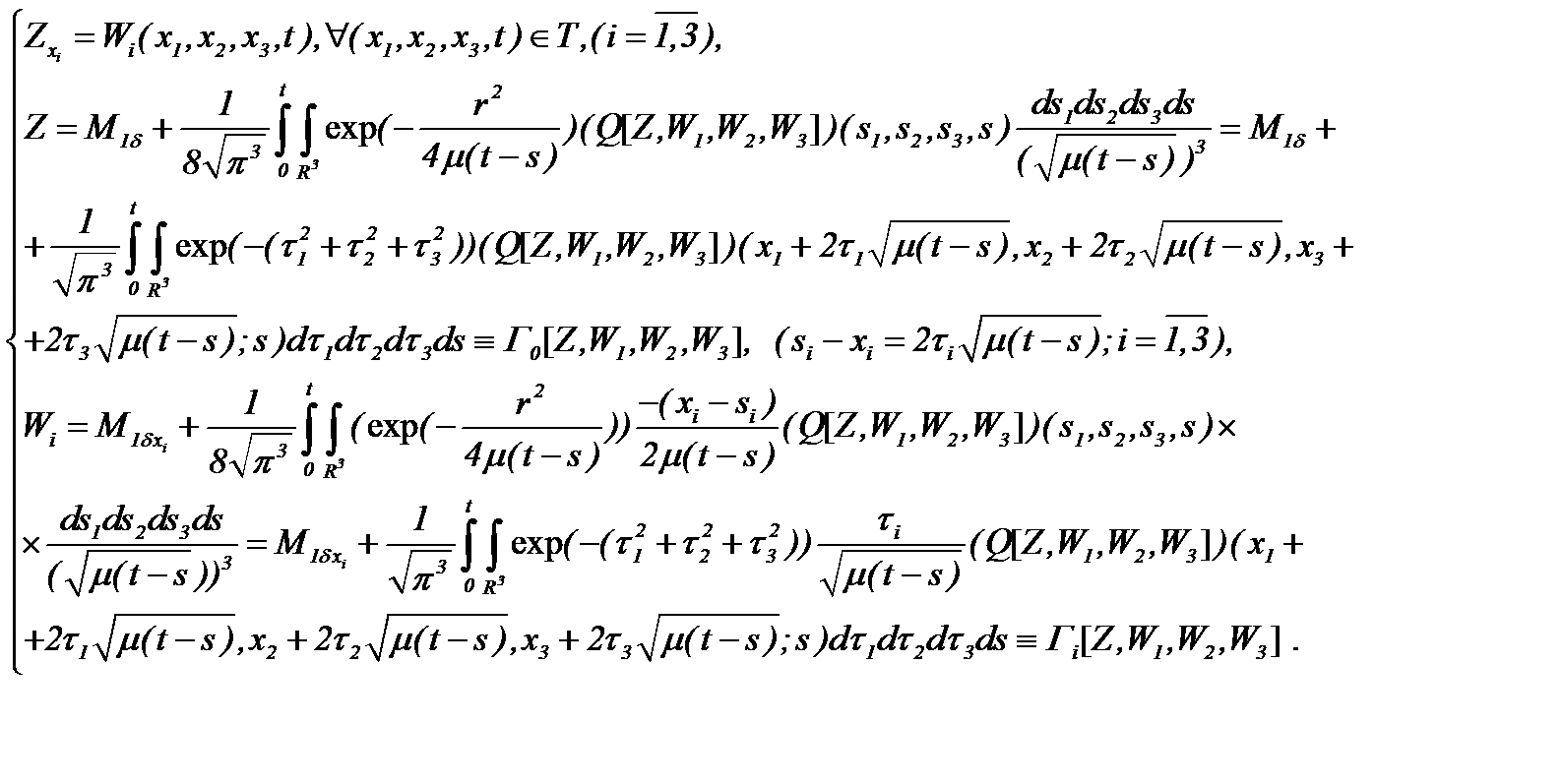(5.42)
Таким образом, для решения задачи (5.40) получили систему (5.42) из четырех интегральных уравнений с четырьмя неизвестными функциями.
Пусть для известных функций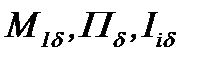 
имеет место
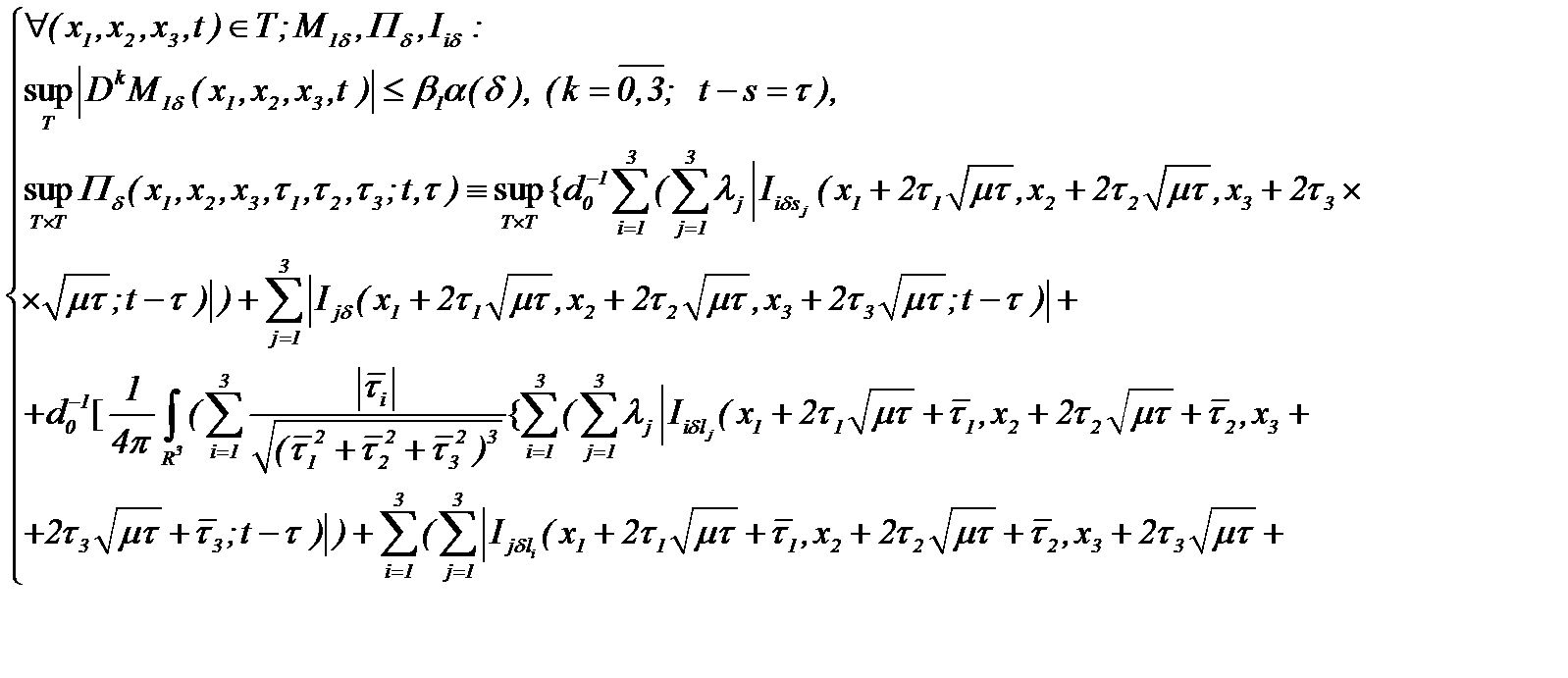
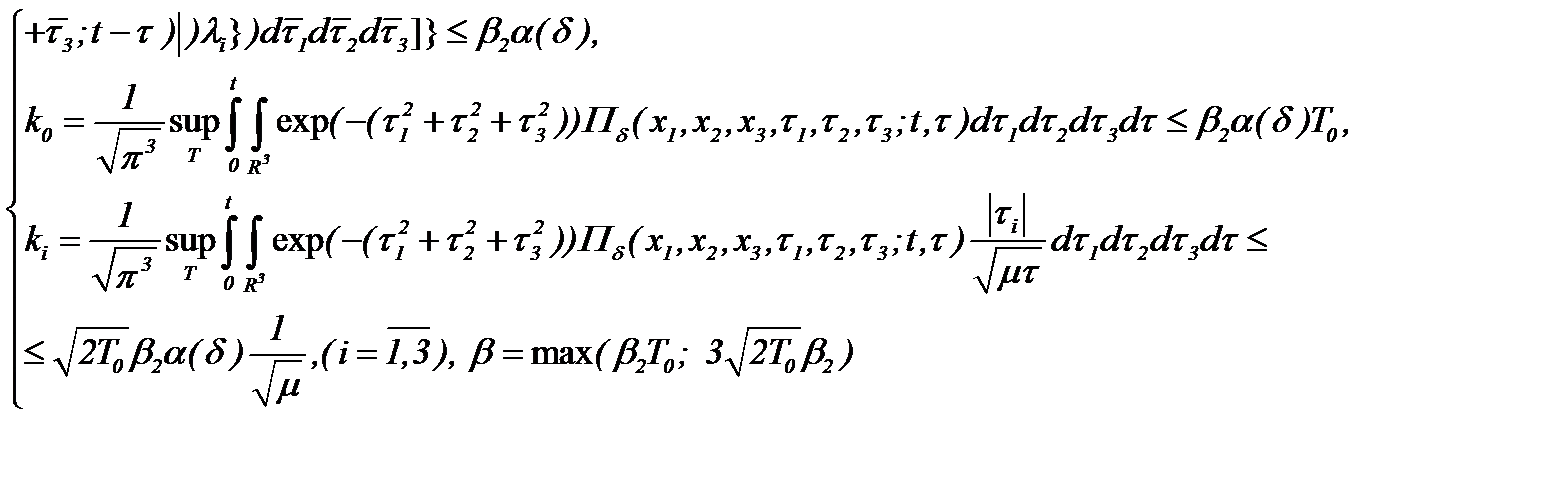(5.43)
и
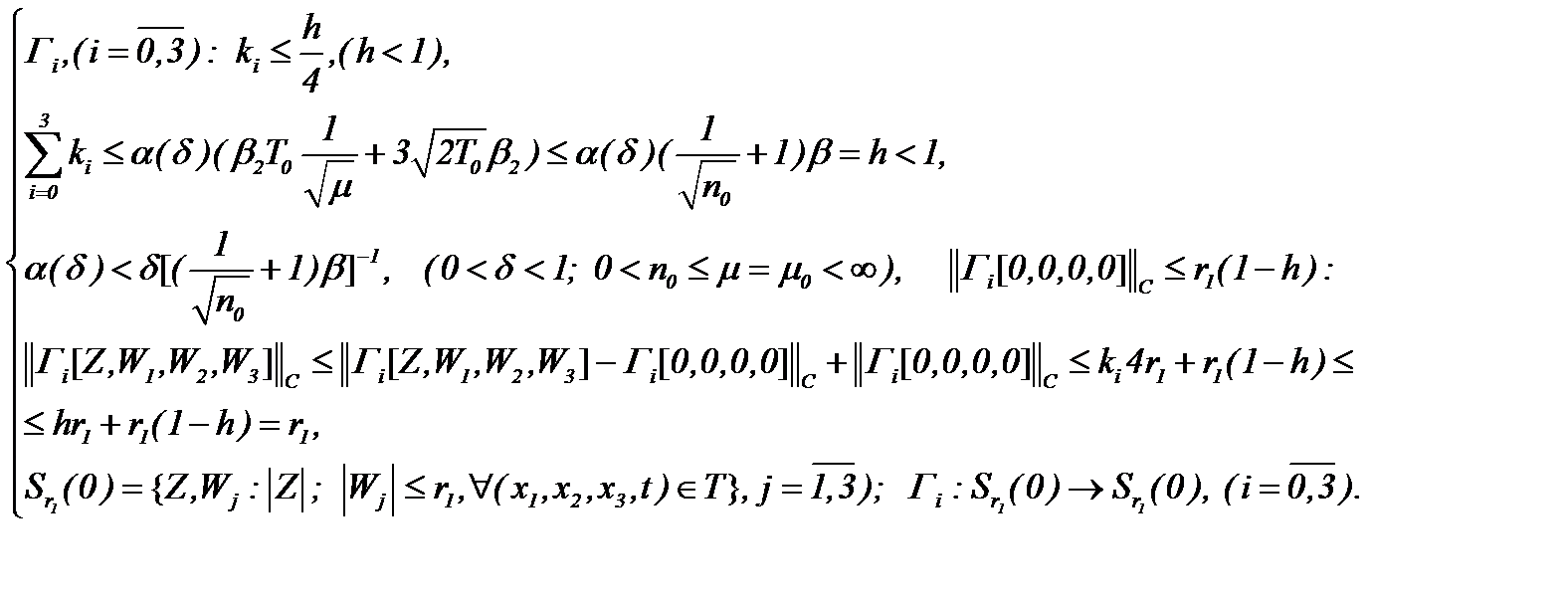(5.44)
Тогда относительно операторов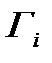 
выполняется принцип сжимающих отображений. Поэтому, система (5.42) разрешима, решение которой строим на основе метода Пикара, а именно
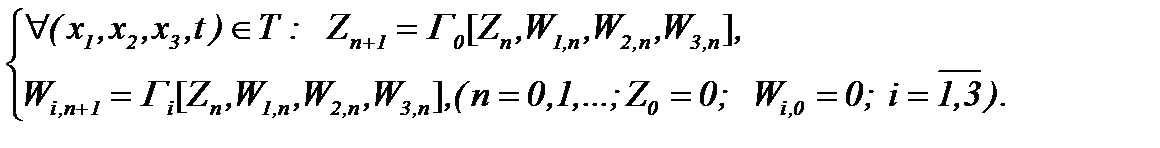(5.45)
Учитывая выводы метода Пикара, имеем
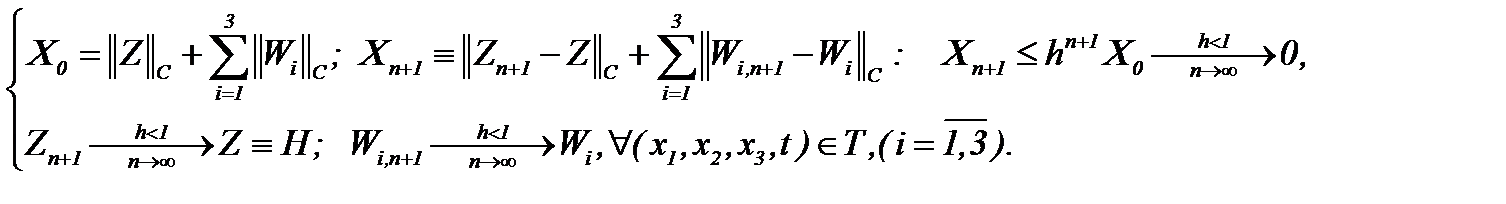(5.46)
Значит, на основании результатов (5.13) – (5.15) получим, что последовательности функций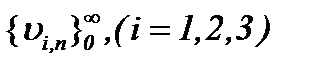 
, построенные по правилу
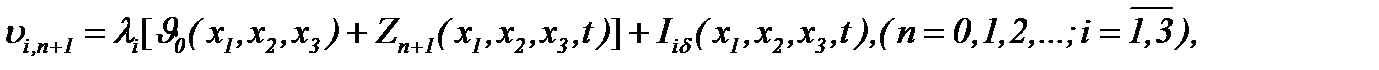(5.47)
сходятся к пределу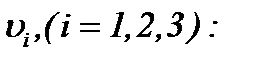 
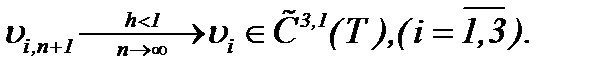(5.48)
Очевидно, малые изменения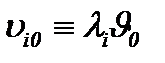 
или 
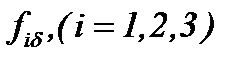не способны влиять на решение
(5.36), значит, решение непрерывно зависит от этих данных. Поэтому корректная постановка задачи (5.31) – (5.33) в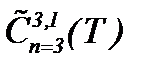 
следует из результатов теоремы 6*.
Отметим, что если же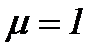 
, причем (см. (5.44)):
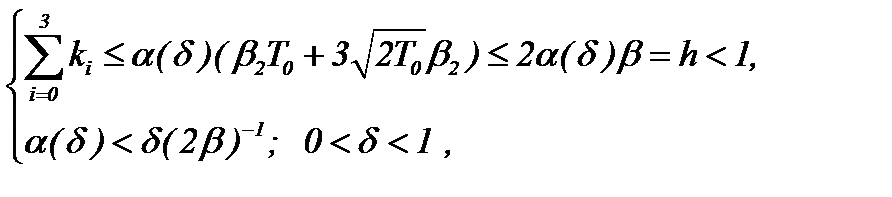
то, очевидно, задача Навье-Стокса (5.31) – (5.33) разрешима в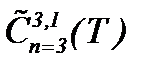 
.
6. Модификация Метода (4.12) на Основе Интегралов Типа Пуассона
В предыдущих параграфах исследованы различные варианты метода (4.12) для задачи Навье-Стокса в пространствах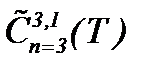 
. Различными исследователями получена связь скорости и давления экспериментальными методами [12]. Например, у Бетца А., Джонса Б.M. и др. связь основана на соотношении типа Бернулли, поэтому скорости 
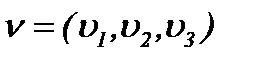выражаются в конкретной форме. В нашем случае для решения 3D уравнений требуется ввести преобразования с помощью интегралов типа Пуассона, что позволит получить соотношение распределения давления, которое даст связь между давлением и скоростью в новой форме, а также позволит выразить скорость в интегральной форме.
В этой связи, в данном пункте рассматривается метод комплексного преобразования на основе интегралов Пуассона, когда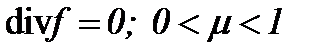 
или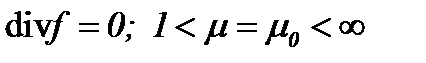 
. Поэтому на основе разработанного метода система Навье-Стокса (1.1) с условиями (1.2) и (1.3) может иметь гладкое единственное решение в 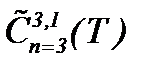, причем в аналитической форме, что и выясним.
6.1. Жидкость с очень малой вязкостью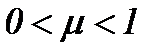 
, когда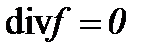 
I . Для несжимаемых течений с трением, если
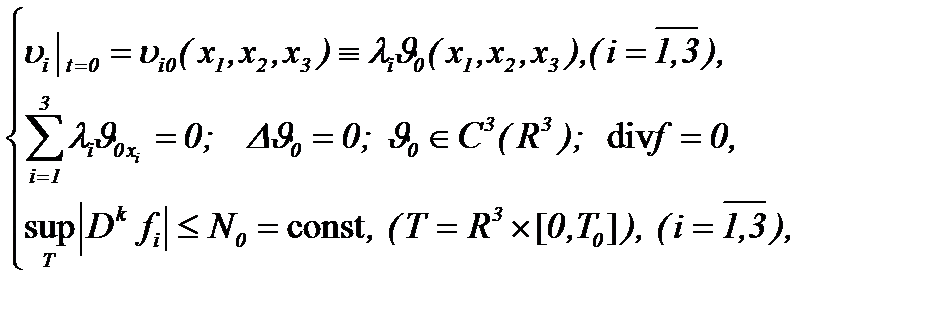(6.1)
то функции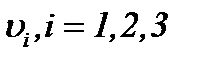 
представимы в виде
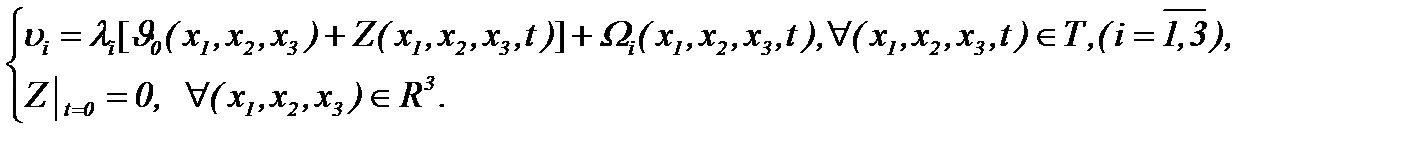(6.2)
От введенных функций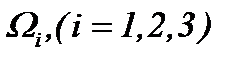 
требуется, чтобы
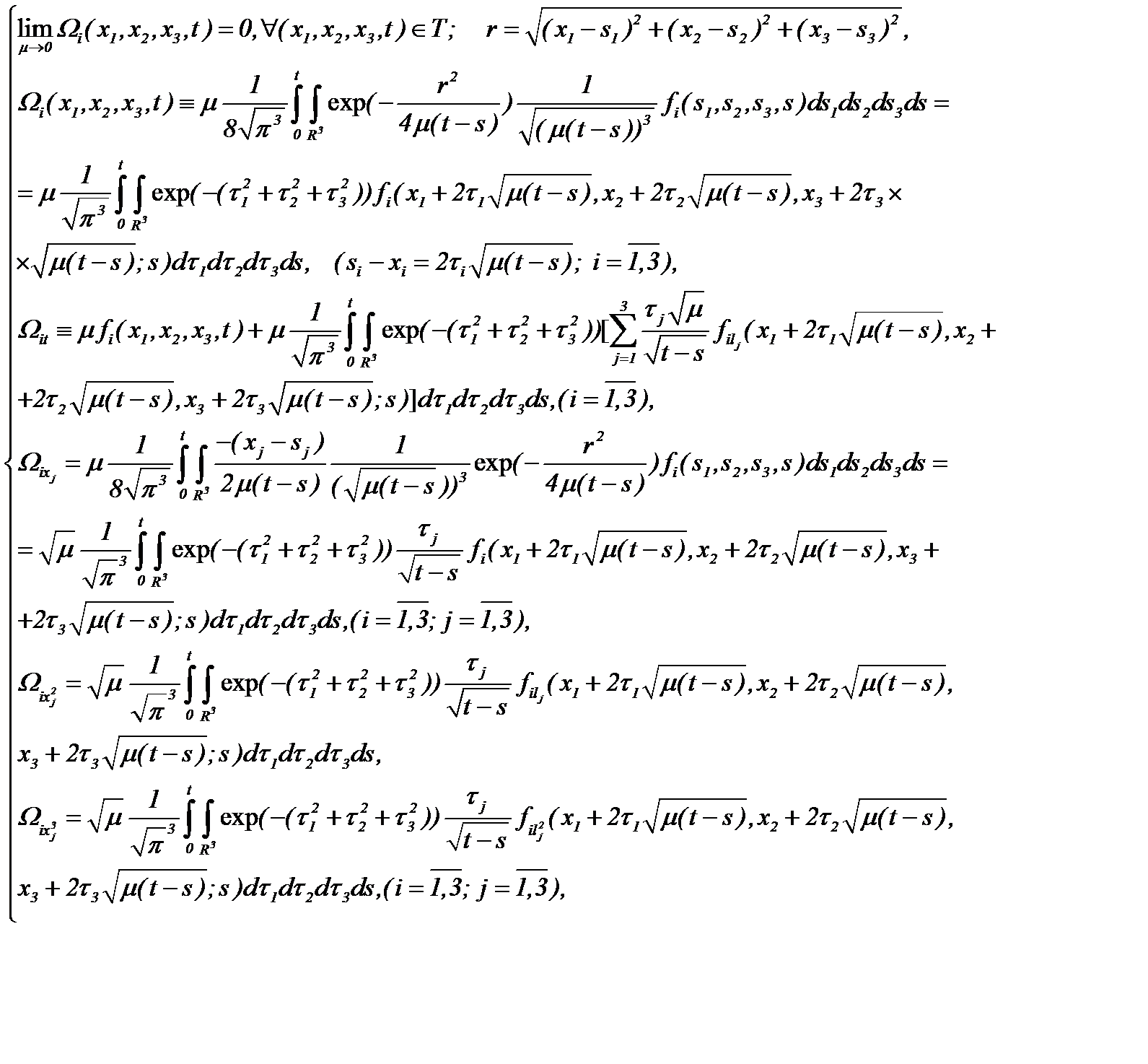
где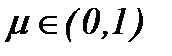 
выступает в роли малого параметра, причем
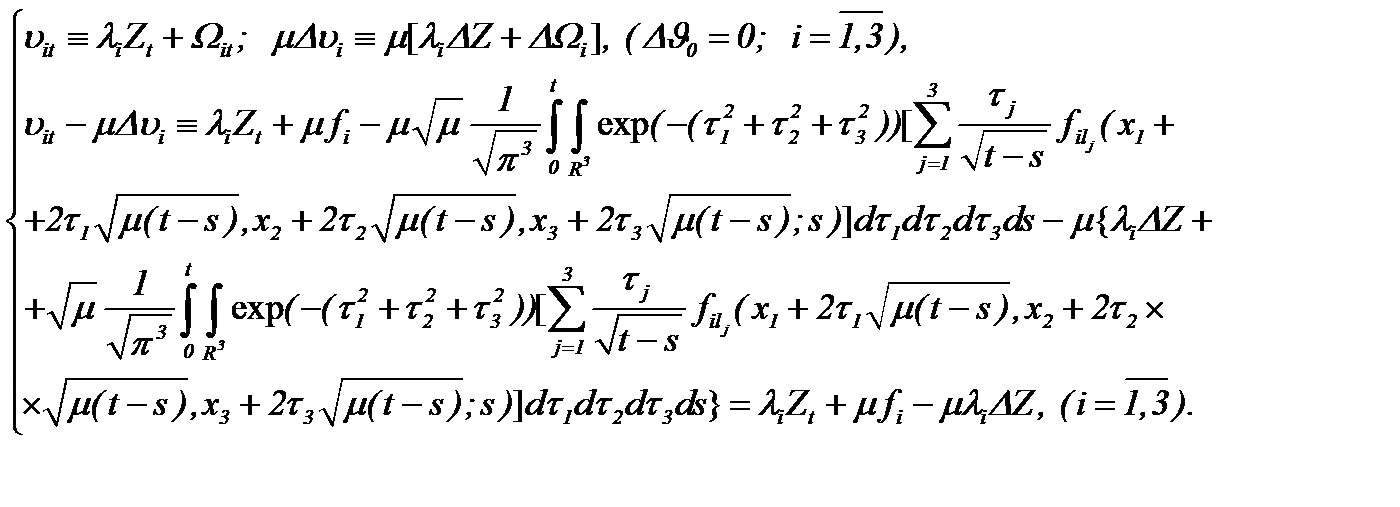(6.3)
Тогда уравнения Навье-Стокса (1.1) для несжимаемых течений с трением трансформируются с помощью (6.1) – (6.3) и принимают следующий вид
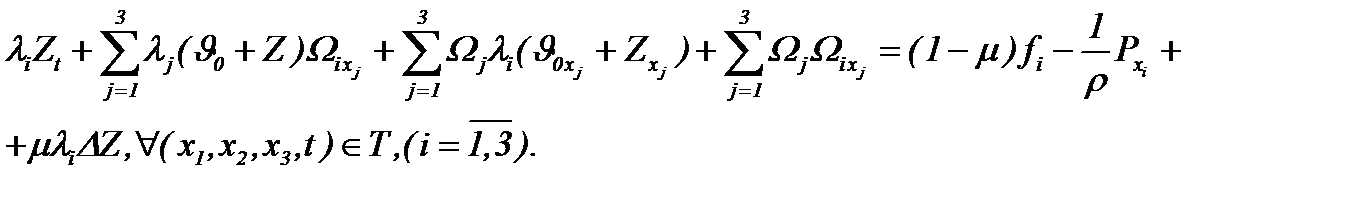(6.4)
Из системы (6.4), учитывая условия (6.1) – (6.3) и применяя АПС, получаем
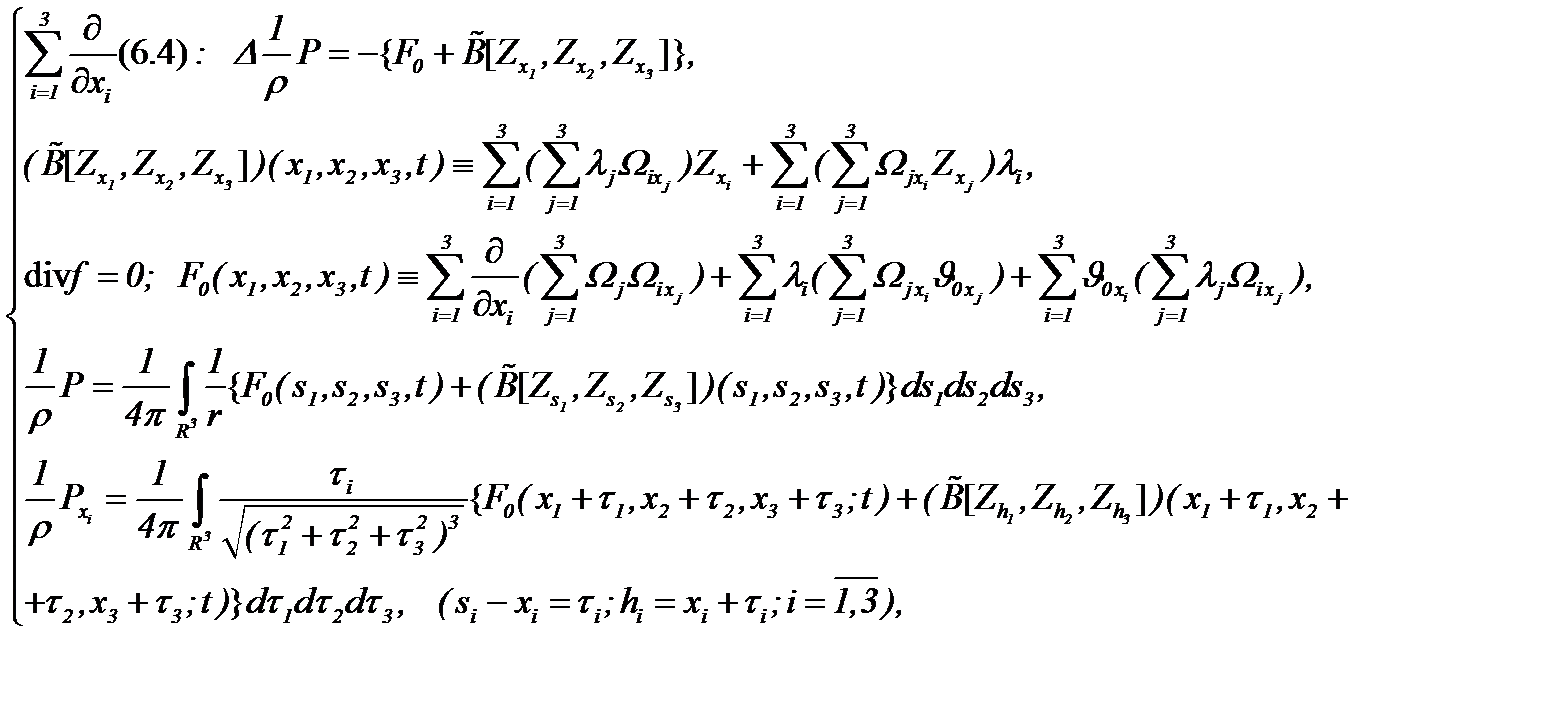(6.5)
так как выполняются условия
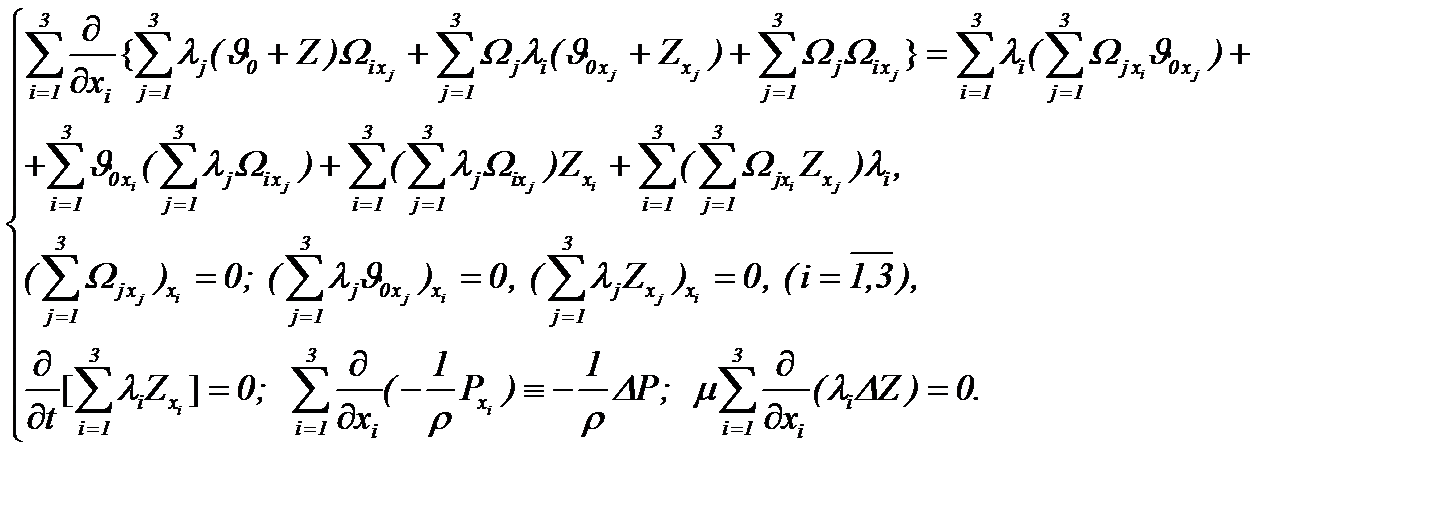
Поэтому, на основе выражения (6.5) система (6.4) эквивалентно преобразуется к виду
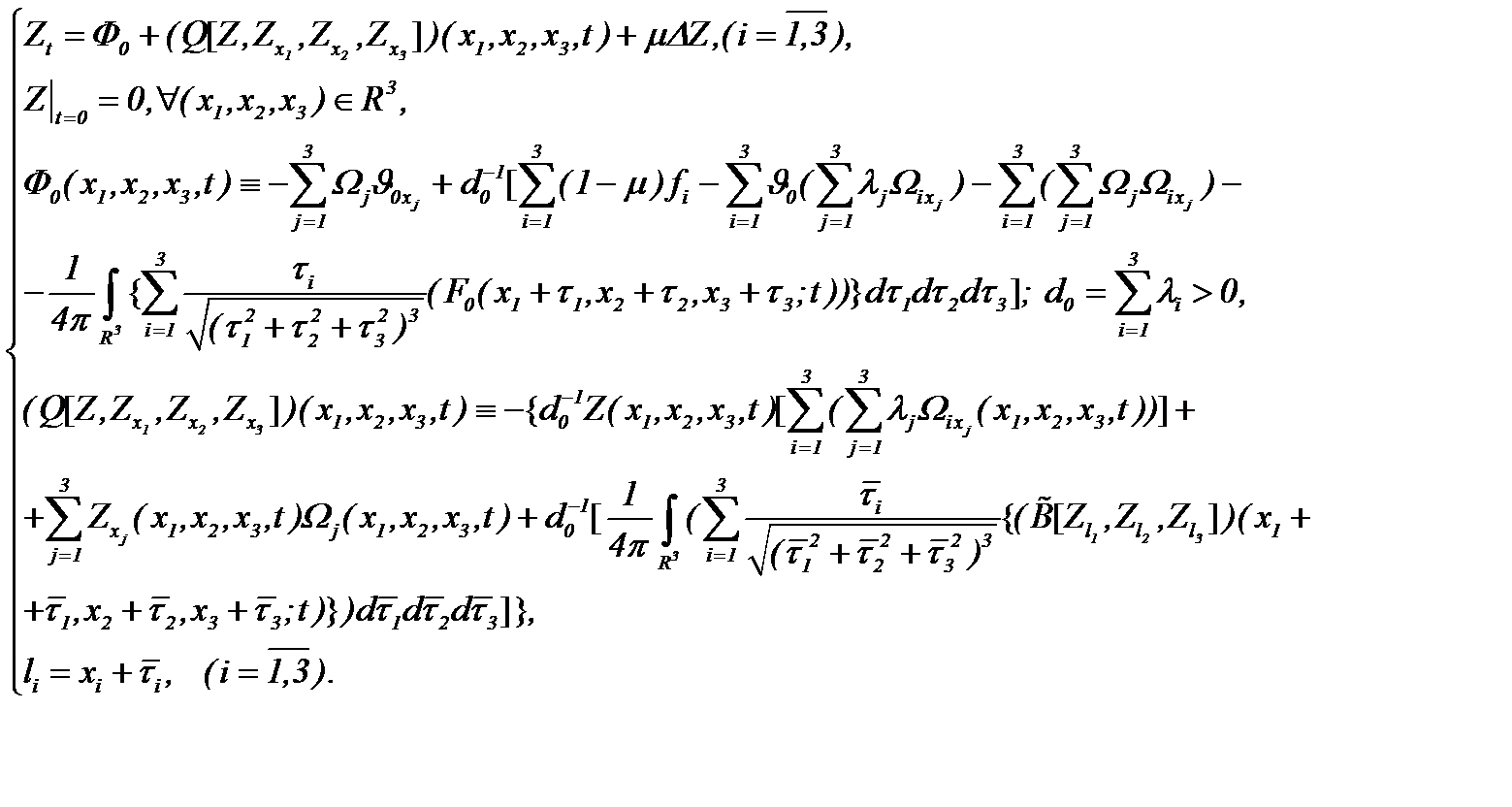(6.6)
Значит, задача (6.6) сводится к системе интегральных уравнений, вполне регулярных относительно параметра вязкости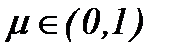 
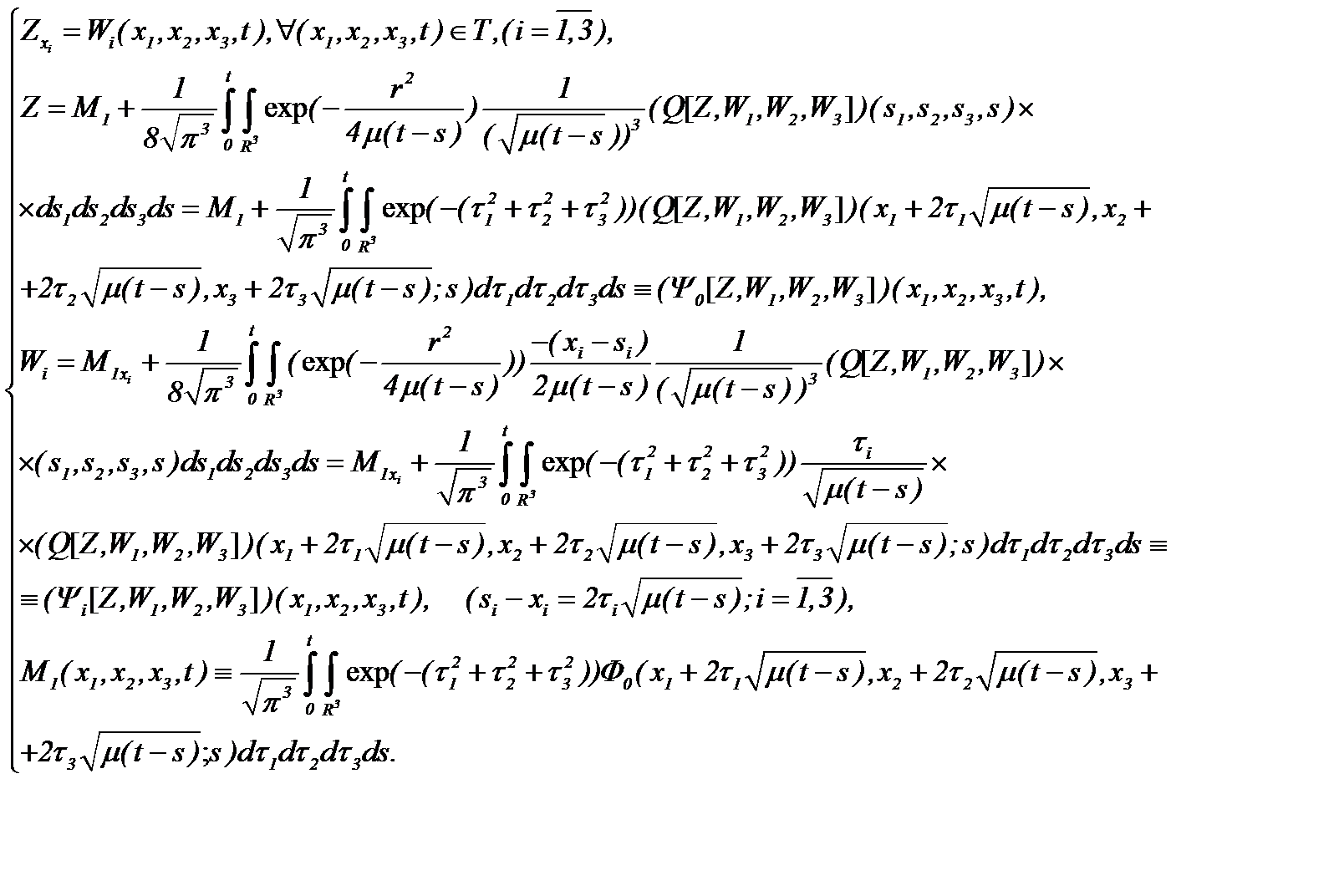(6.7)
Пусть известные функции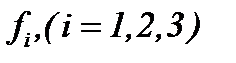 
являются субмультипликативными функциями [15] и имеет место
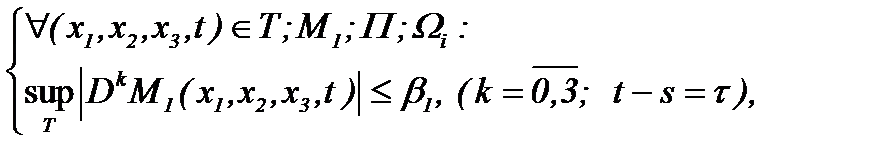
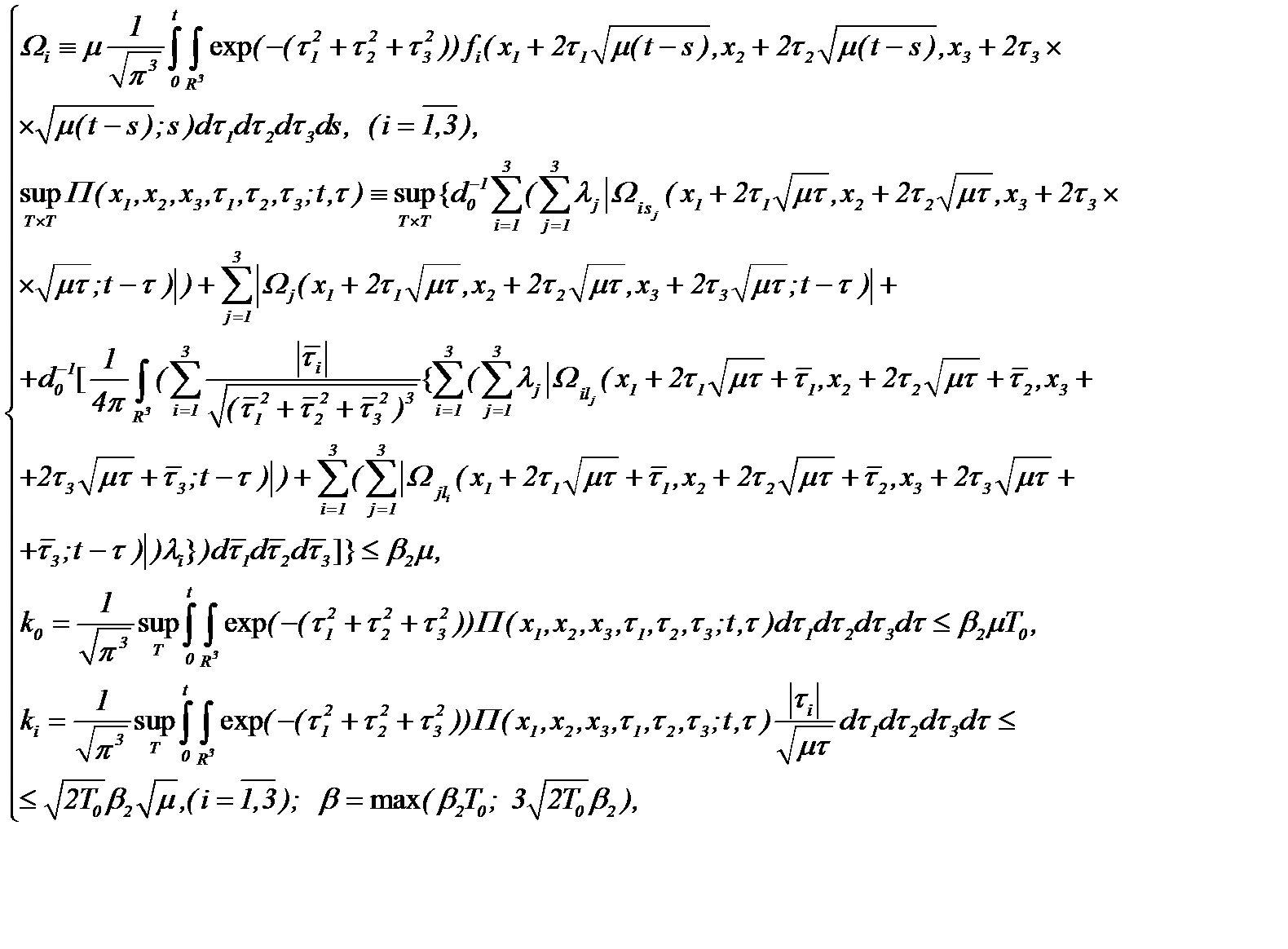(6.8)
причем операторы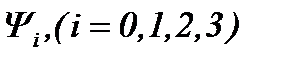 
допускают условия принципа сжимающих отображений:
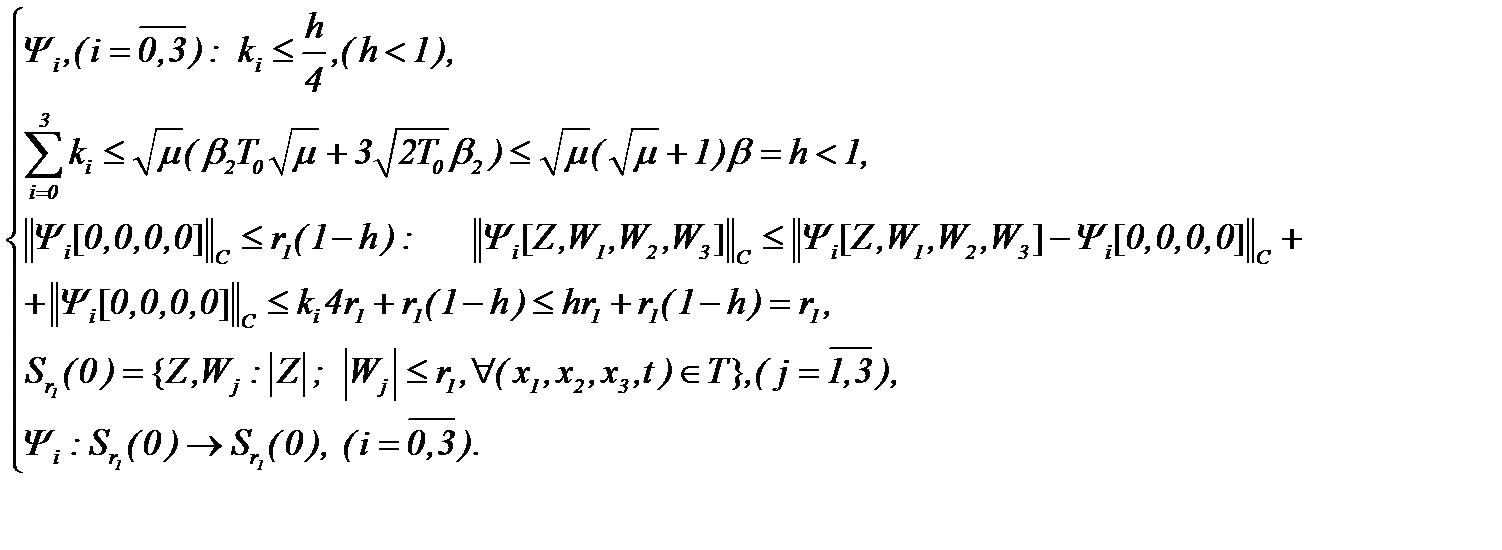(6.9)
Тогда система (6.7) однозначно разрешима, а решение этой системы можем найти на основе метода Пикара
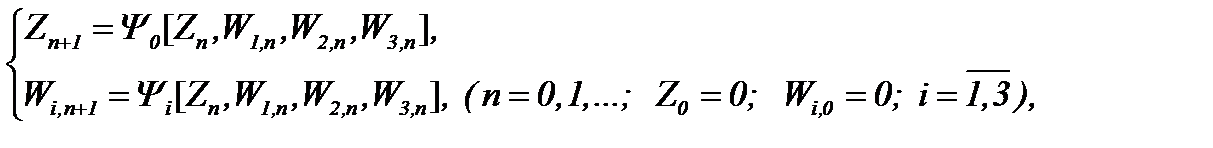(6.10)
при этом имеет место
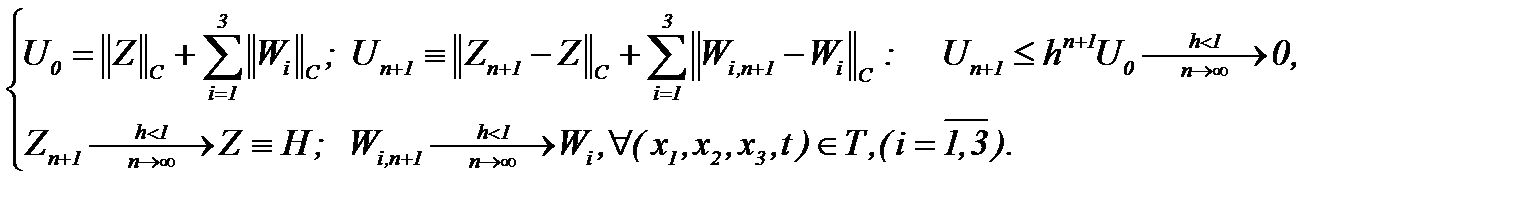(6.11)
Поэтому на основании (6.2) и
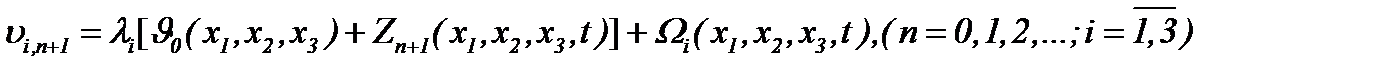(6.12)
получим
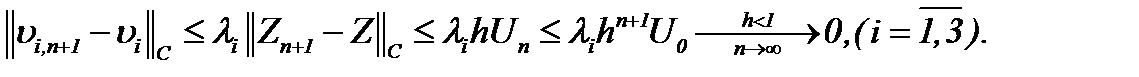(6.13)
Это значит, что последовательность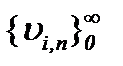 
сходится к пределу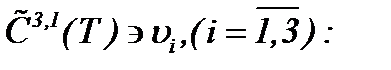 
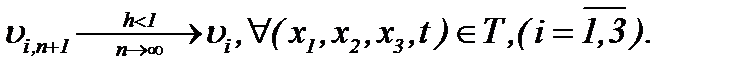(6.14)
А потому задача Навье-Стокса при условиях (1.2), (6.1), (6.2), (6.8), (6.9) и (6.14) имеет гладкое единственное решение вида (6.2) в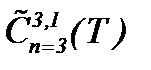 
.
Жидкость с вязкостью, когда div f = 0
6.2. Жидкость с вязкостью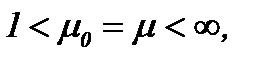 
когда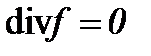 
В параграфе 5 были исследованы уравнения Навье-Стокса с вязкостью среднего размера, при этом введенные математические преобразования свели нелинейные члены конвективного ускорения к линейному виду. Тем самым, с помощью новой теории получены неоднородные линейные уравнения теплопроводности с условием Коши.
Для развития предлагаемой теории рассмотрим аналогичные задачи для жидкости с небольшим числом Рейнольдса и со всеми членами конвективного ускорения в уравнениях Навье-Стокса. В отличие от параграфа 5 будем рассматривать методы интегральных преобразований на основе интегралов типа Пуассона в 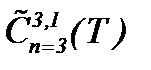, когда 
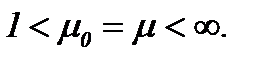Метод аналитического решения уравнений Навье-Стокса, который дает интегрируемость этих уравнений, применяется в случае
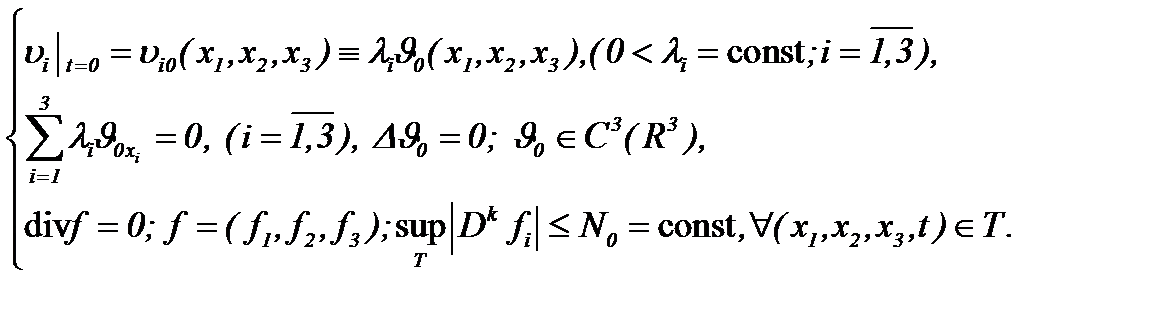(6.15)
На основании чего, вводим формулу для определения компонент скоростей:
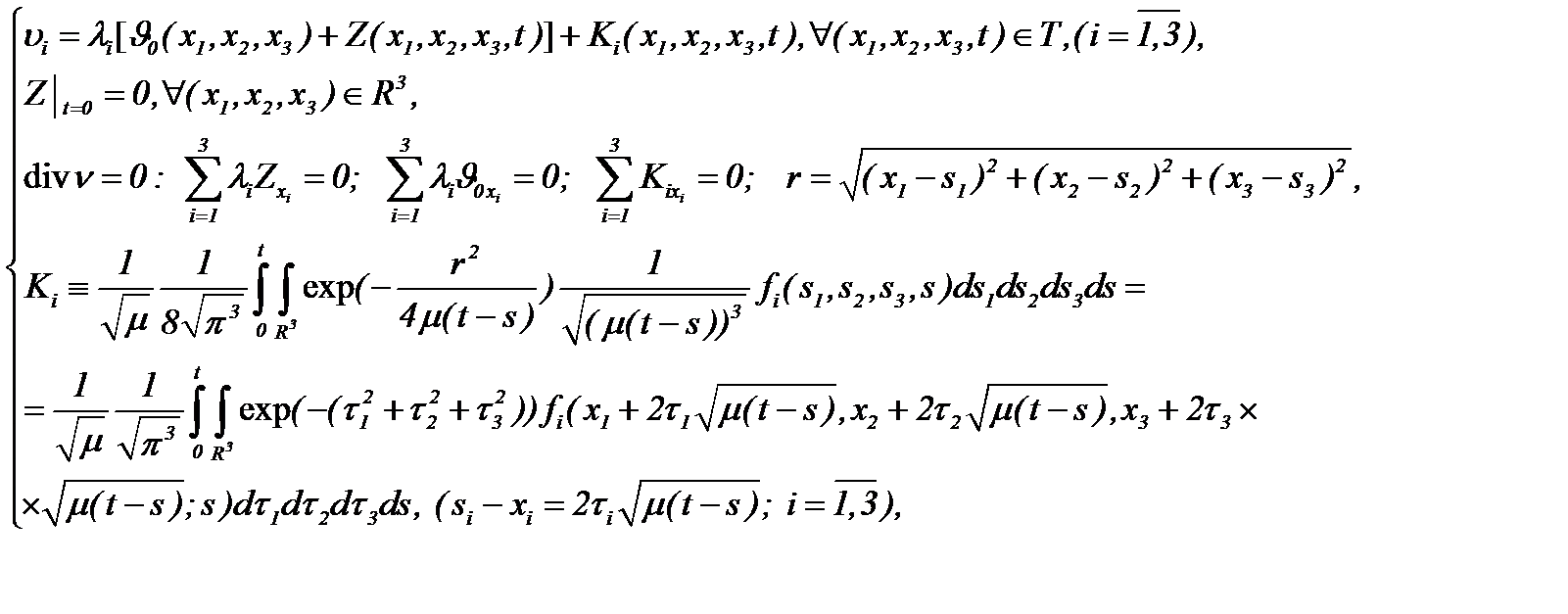(6.16)
причем
(6.17)
Следовательно, с помощью (6.15) – (6.17) система Навье-Стокса (1.1) сводится к виду
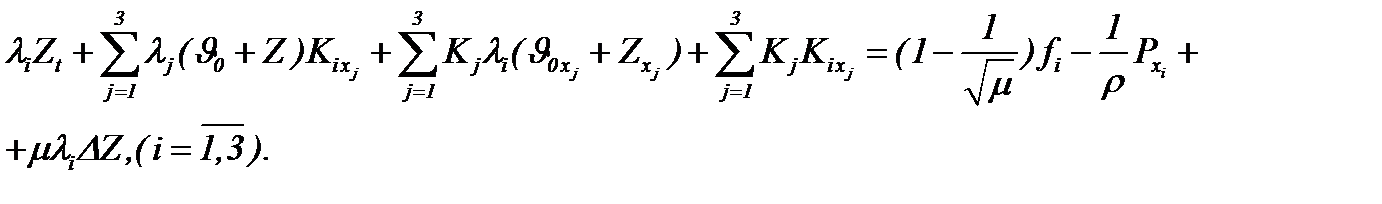(6.18)
Поэтому из системы (6.18) с учетом (6.5) – (6.7), где вместо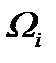 
рассматриваем 
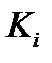, получим
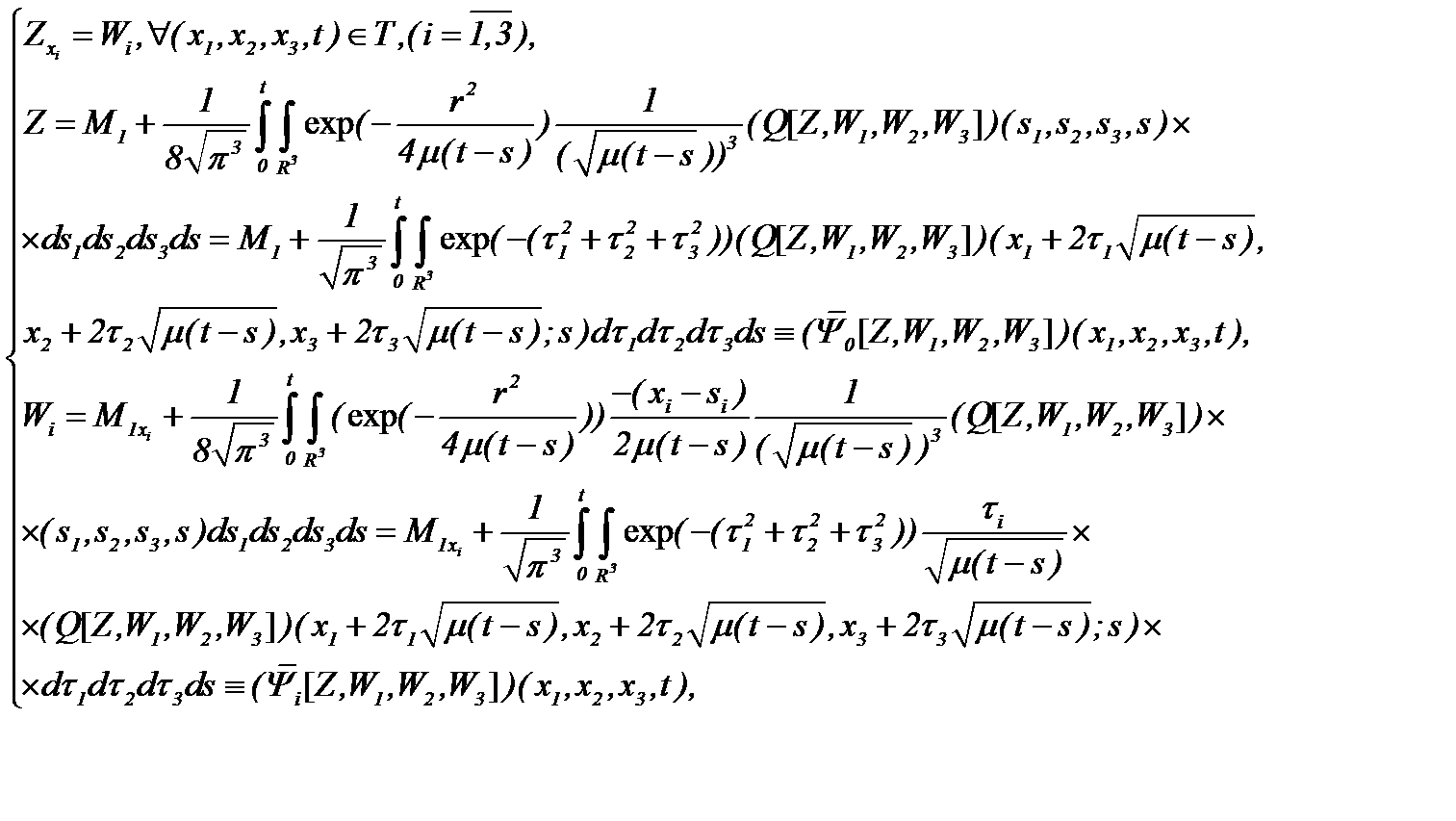(6.19)
в которых
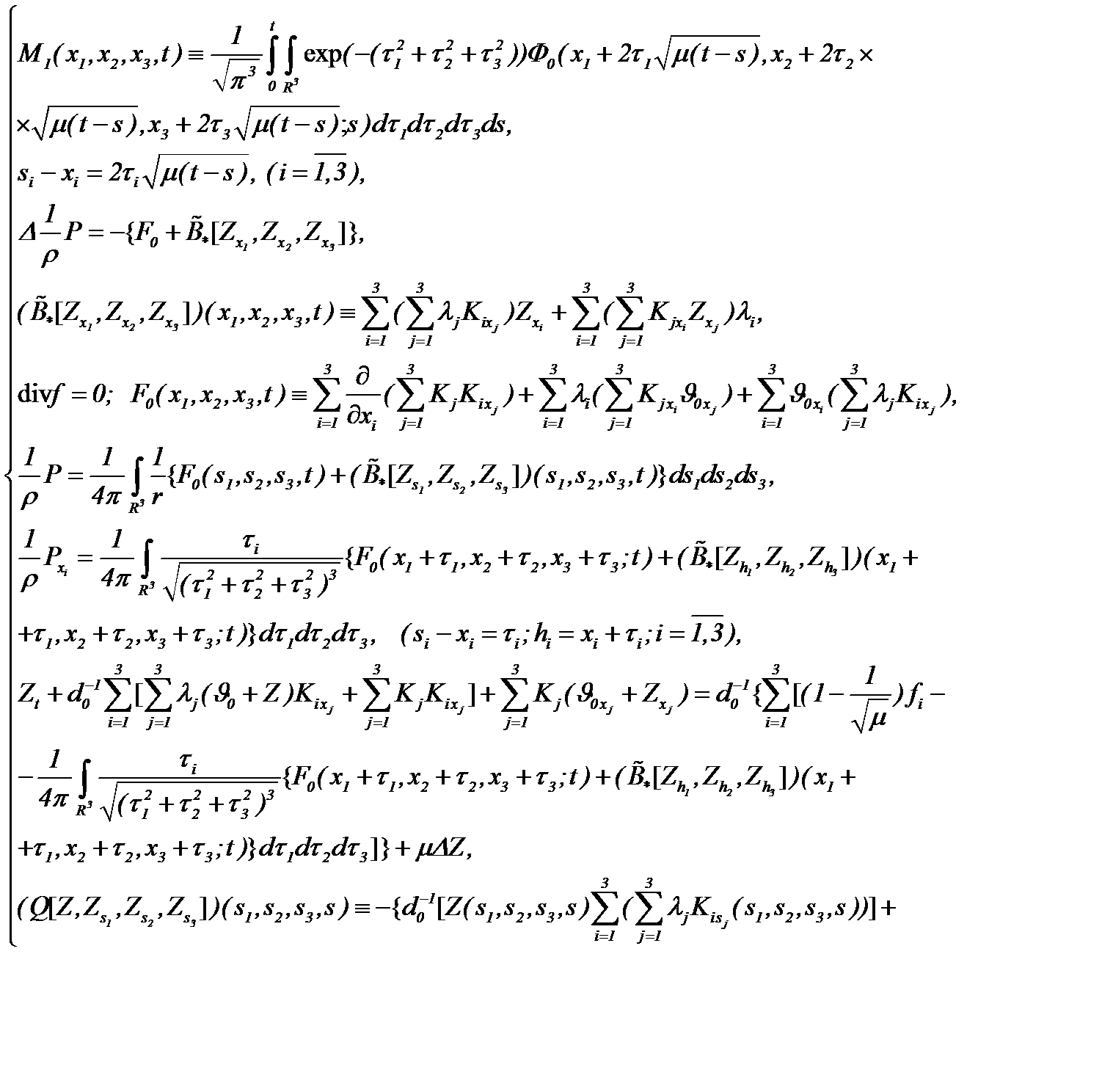
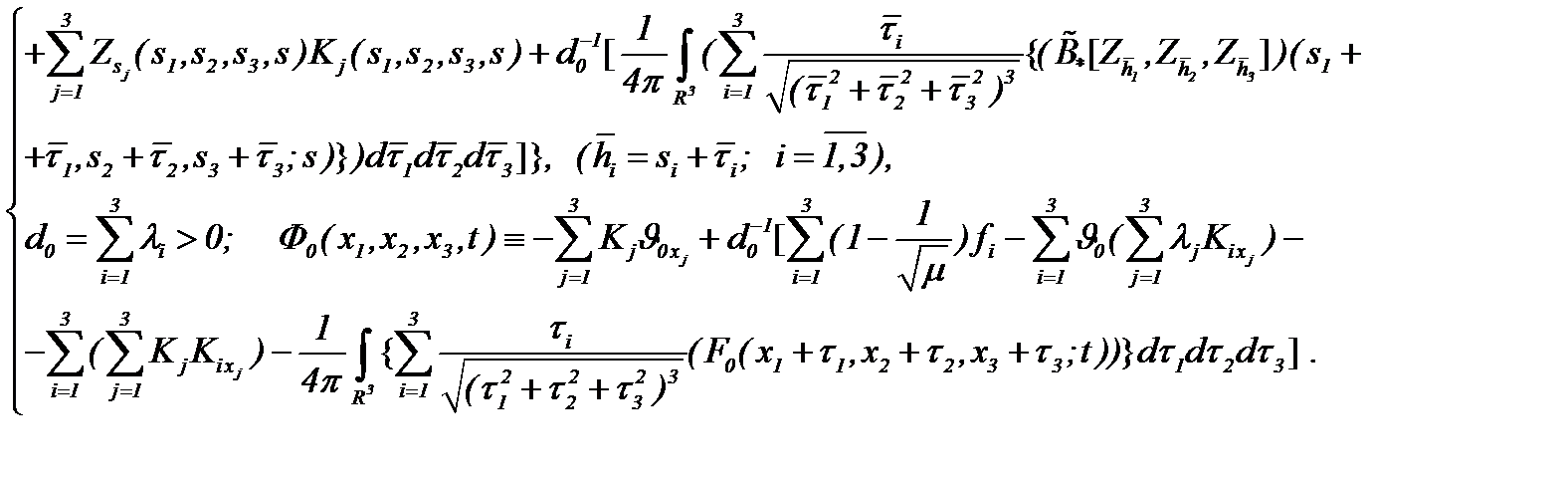
Если имеет место
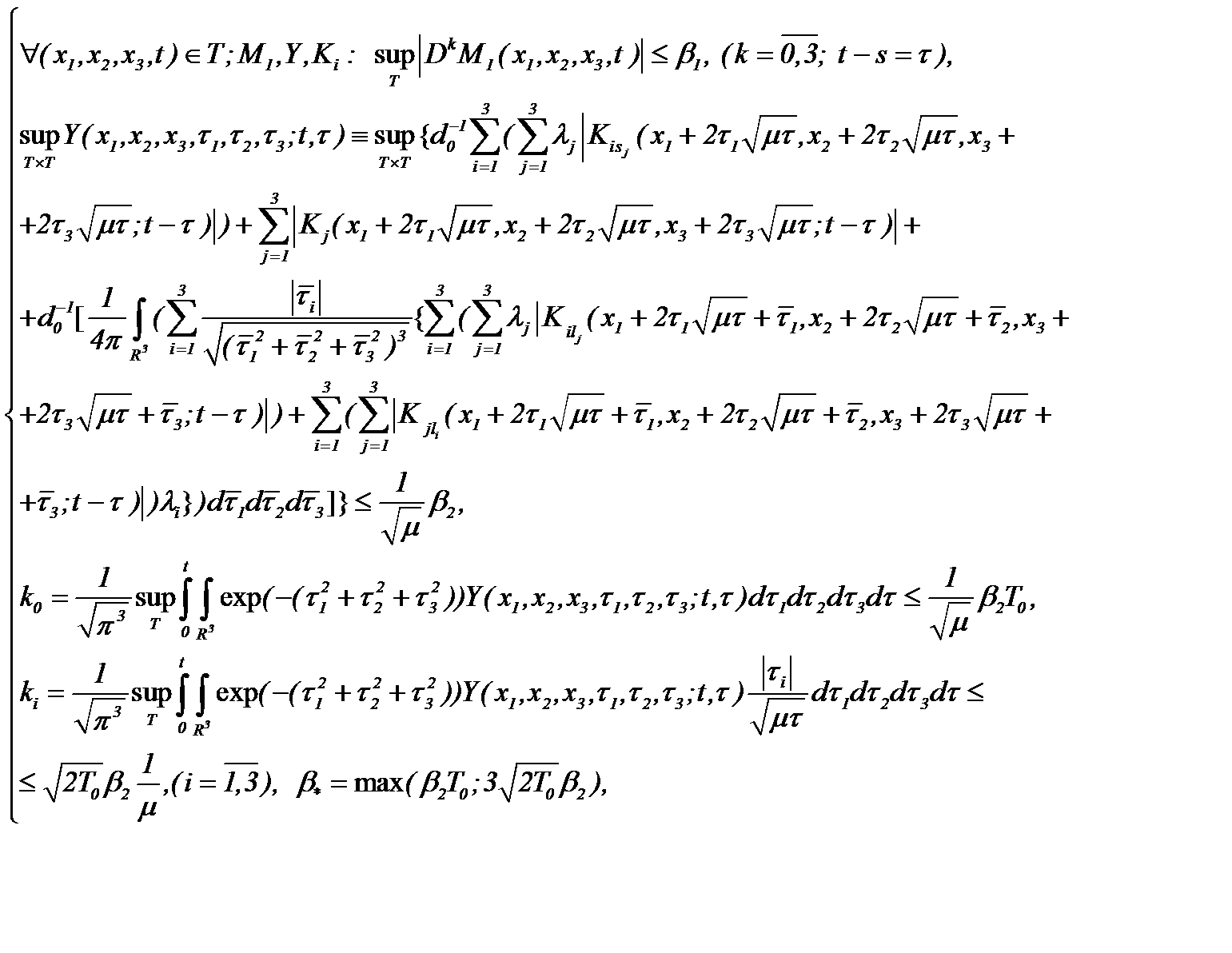(6.20)
а операторы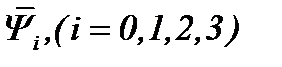 
допускают условия
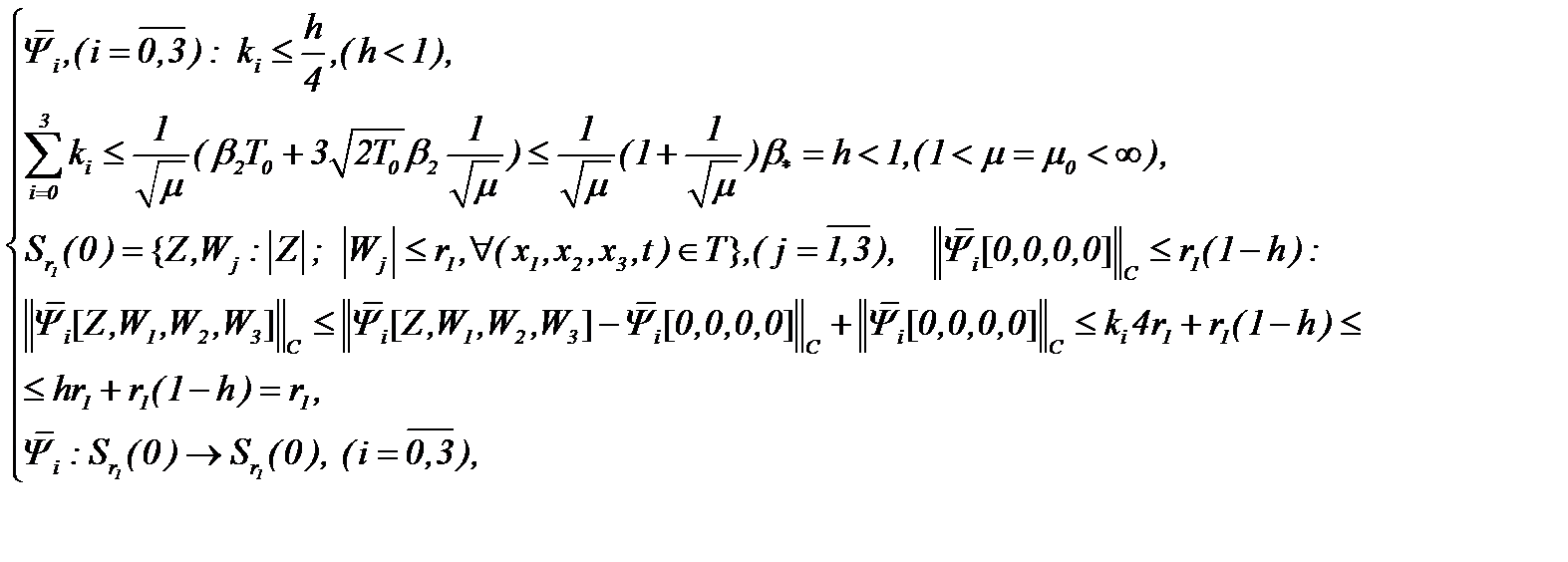(6.21)
то относительно этих операторов выполняются условия сжимающих отображений. Это означает, что система (6.19) однозначно разрешима, а решение данной системы определяется по методу Пикара (6.10). Тогда с учетом результатов (6.11) – (6.14) получим, что последовательности функций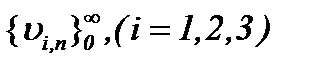 
сходятся к пределу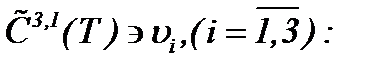 
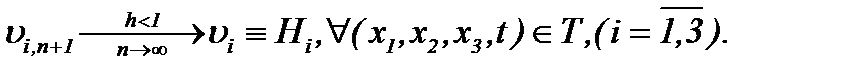(6.22)
Как следствие пунктов 6.1 и 6.2, получим следующие утверждения.
Теорема 7. Нестационарная задача Навье-Стокса (1.1) – (1.3) разрешима в 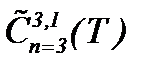, когда
выполнены условия:
a ) (6.1), (6.2), (6.8), (6.9), (6.14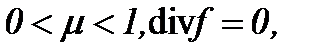) и 
или
б) (6.15) – (6.17), (6.20), (6.21), (6.22) и 