Жидкость со средней вязкостью с условием
5. Жидкость с Вязкостью 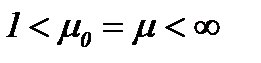
Рассмотрим вязкую жидкость с небольшим числом Рейнольдса, где все инерционные члены содержатся в уравнениях Навье-Стокса для несжимаемой жидкости с вязкостью [12]. Выше отмечено, что уравнения Навье-Стокса такого вида, если не считать работы [8, 9], не исследованы в полном объеме. Технические приложения теории жидкости ограничены при очень больших значениях вязкости, если не поднимать вопросы теории смазки и падение маленьких шариков в густом масле [12]. Однако теоретические исследования в этом направлении важны для науки и практики. Это вызывает к разработке методов интегрирования уравнений Навье-Стокса со средним размером вязкости при наличии всех членов уравнения, поэтому в данном параграфе разработаны методы решения таких задач в пространстве 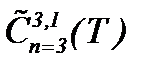 и класс подходящих решений, построенных на основе леммы K. Фридрихса [15] в
и класс подходящих решений, построенных на основе леммы K. Фридрихса [15] в 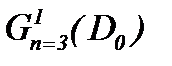 .
.
Для этого модифицируются основные методы параграфа 4: (4.2) и (4.12) на основе регулирующих функций 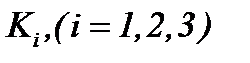 , причем задача (1.1) – (1.3) не допускает ограничений (А1) и (А2), в чем и заключается актуальность исследований этого параграфа.
, причем задача (1.1) – (1.3) не допускает ограничений (А1) и (А2), в чем и заключается актуальность исследований этого параграфа.
5.1. Жидкость со средней вязкостью с условием 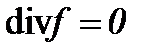
Итак, если исходные данные 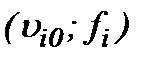 подчинены условию
подчинены условию
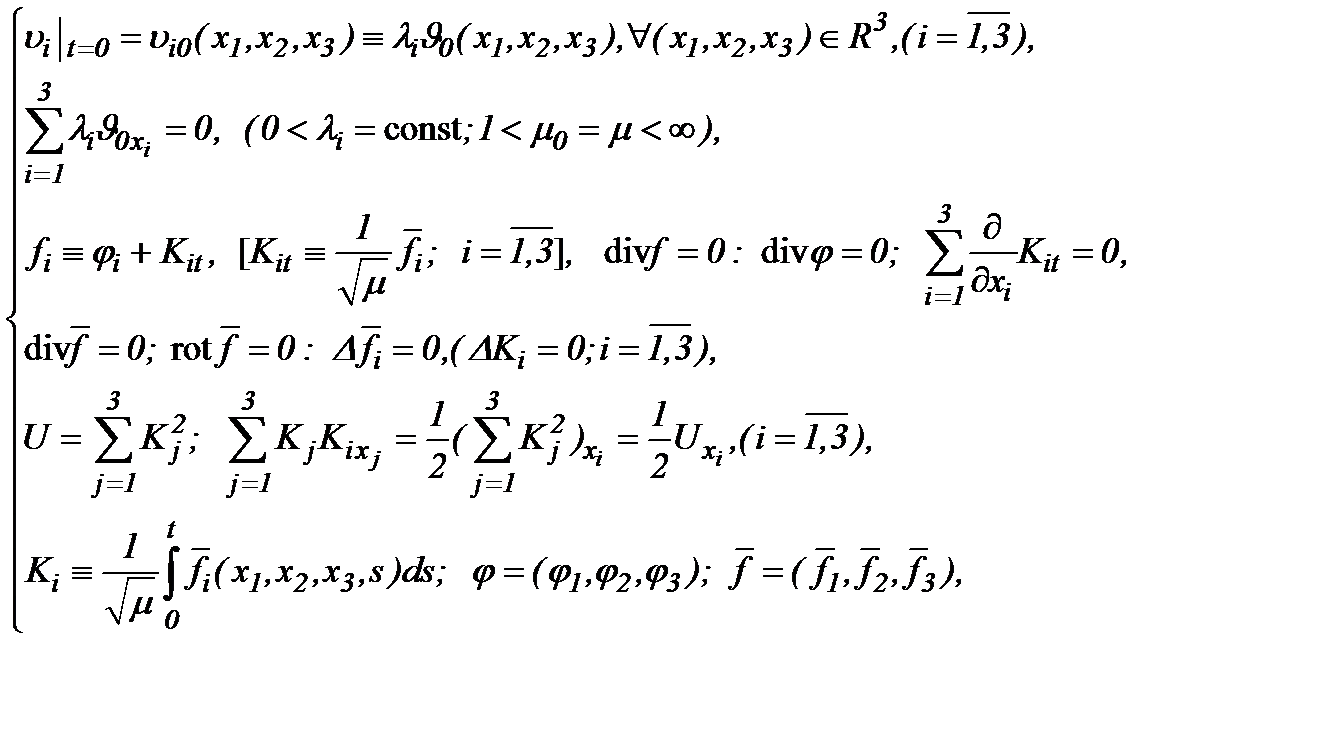 (5.1)
(5.1)
то для определения компонент скоростей введем следующее правило
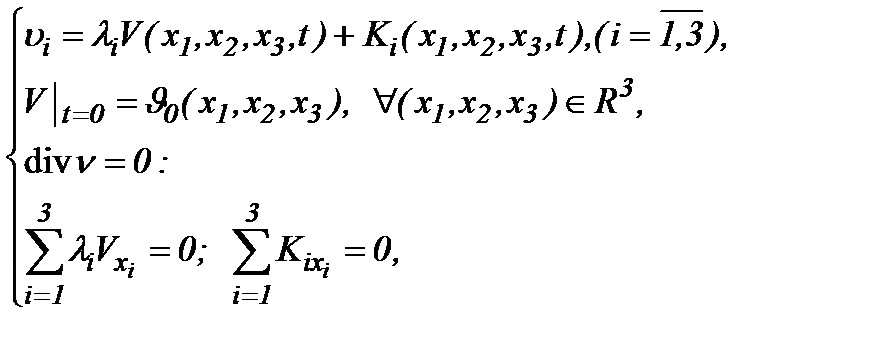 (5.2)
(5.2)
причем
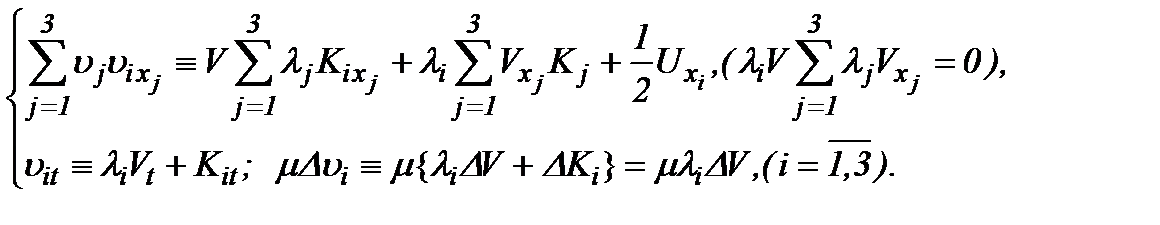 (5.3)
(5.3)
Тогда, принимая во внимание (5.2) и (5.3), получим
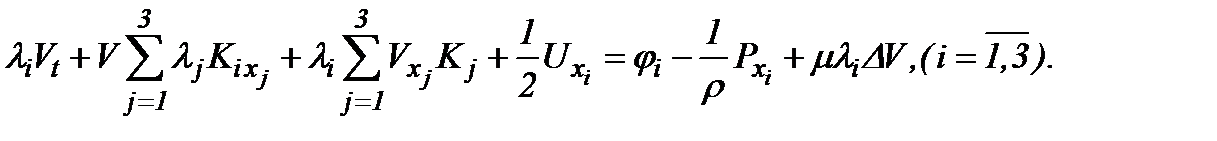 (5.4)
(5.4)
Значит, на основании (5.4) имеем
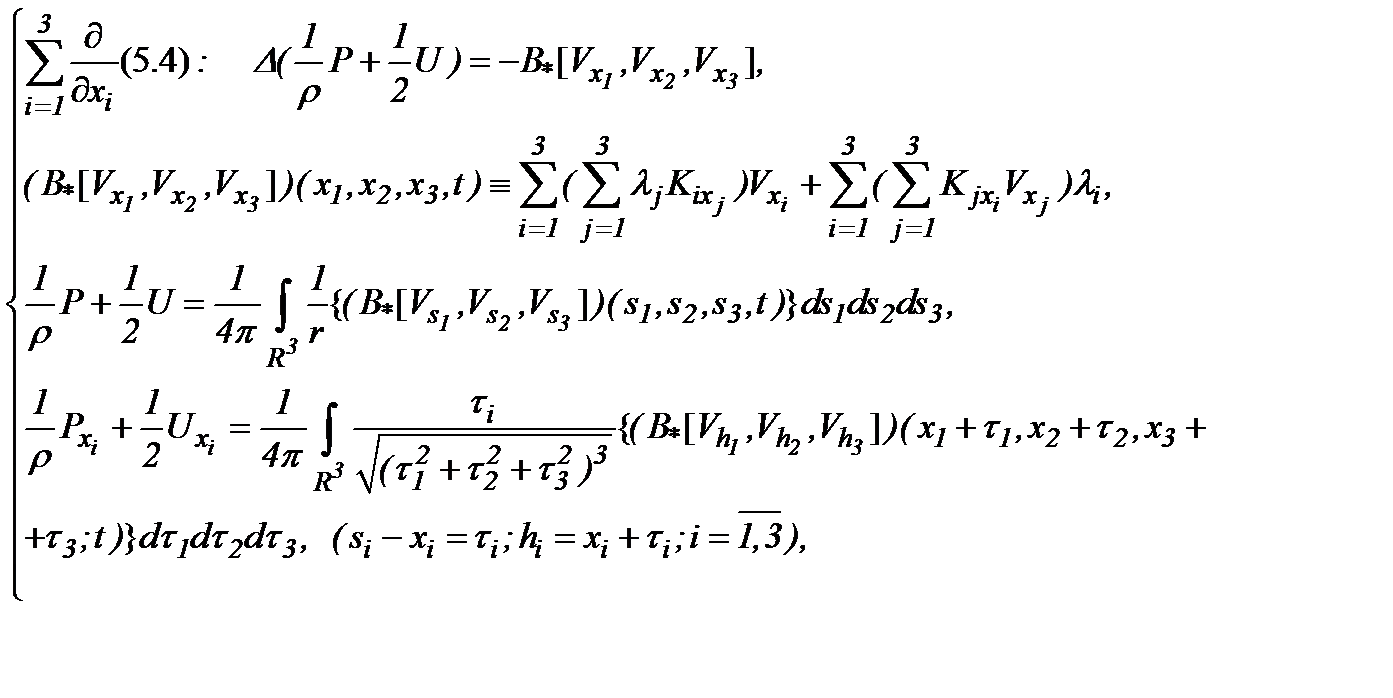 (5.5)
(5.5)
так как имеет место
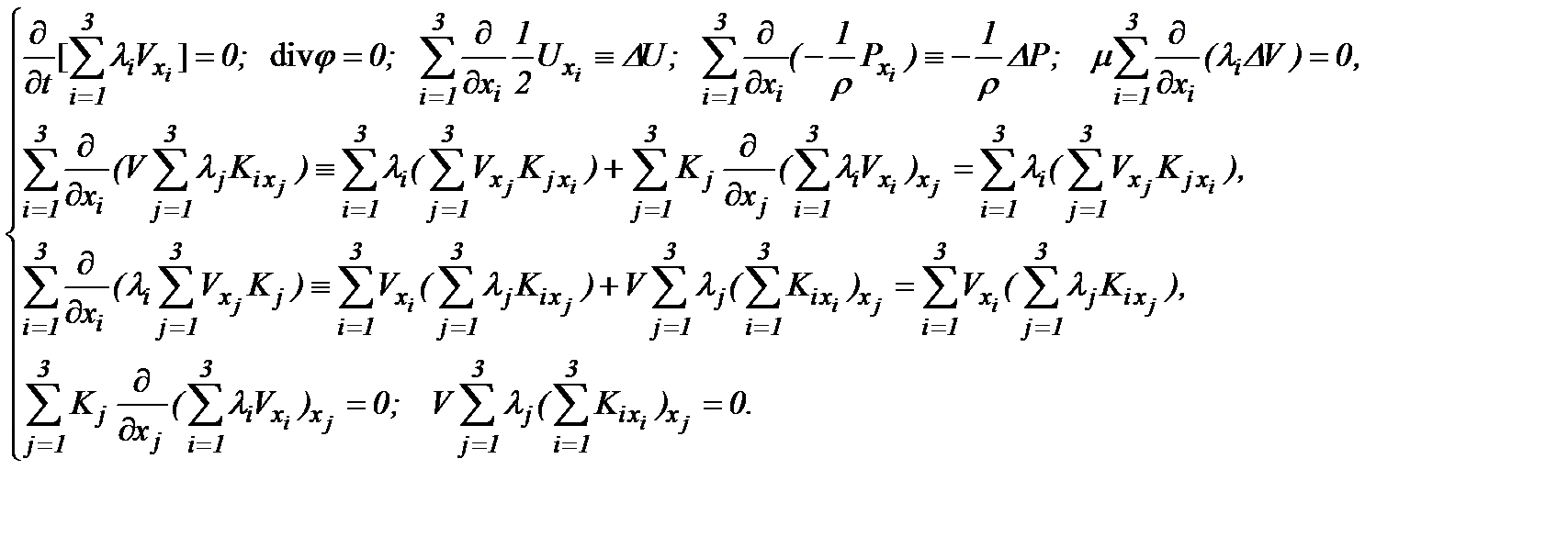
Тогда систему (5.4) можно эквивалентно преобразовать к виду
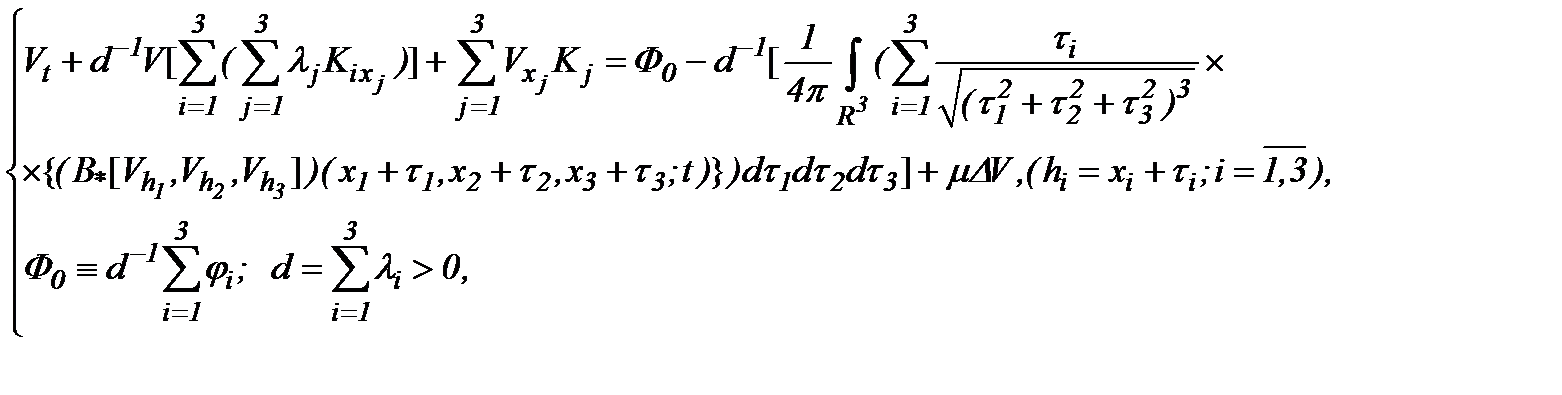 (5.6)
(5.6)
т.е. заменить одним уравнением с одной неизвестной 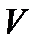 . Следовательно, неизвестная функция
. Следовательно, неизвестная функция 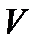 определяется уравнением
определяется уравнением
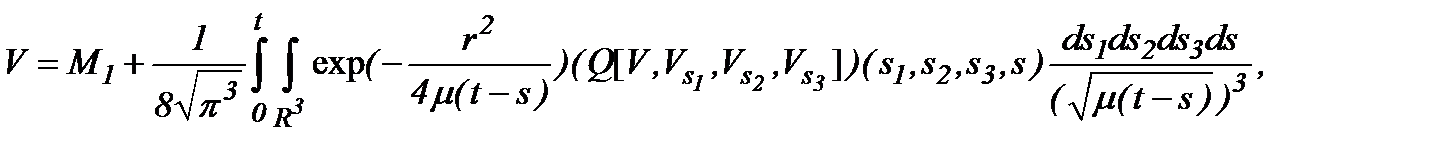 (5.7)
(5.7)
где
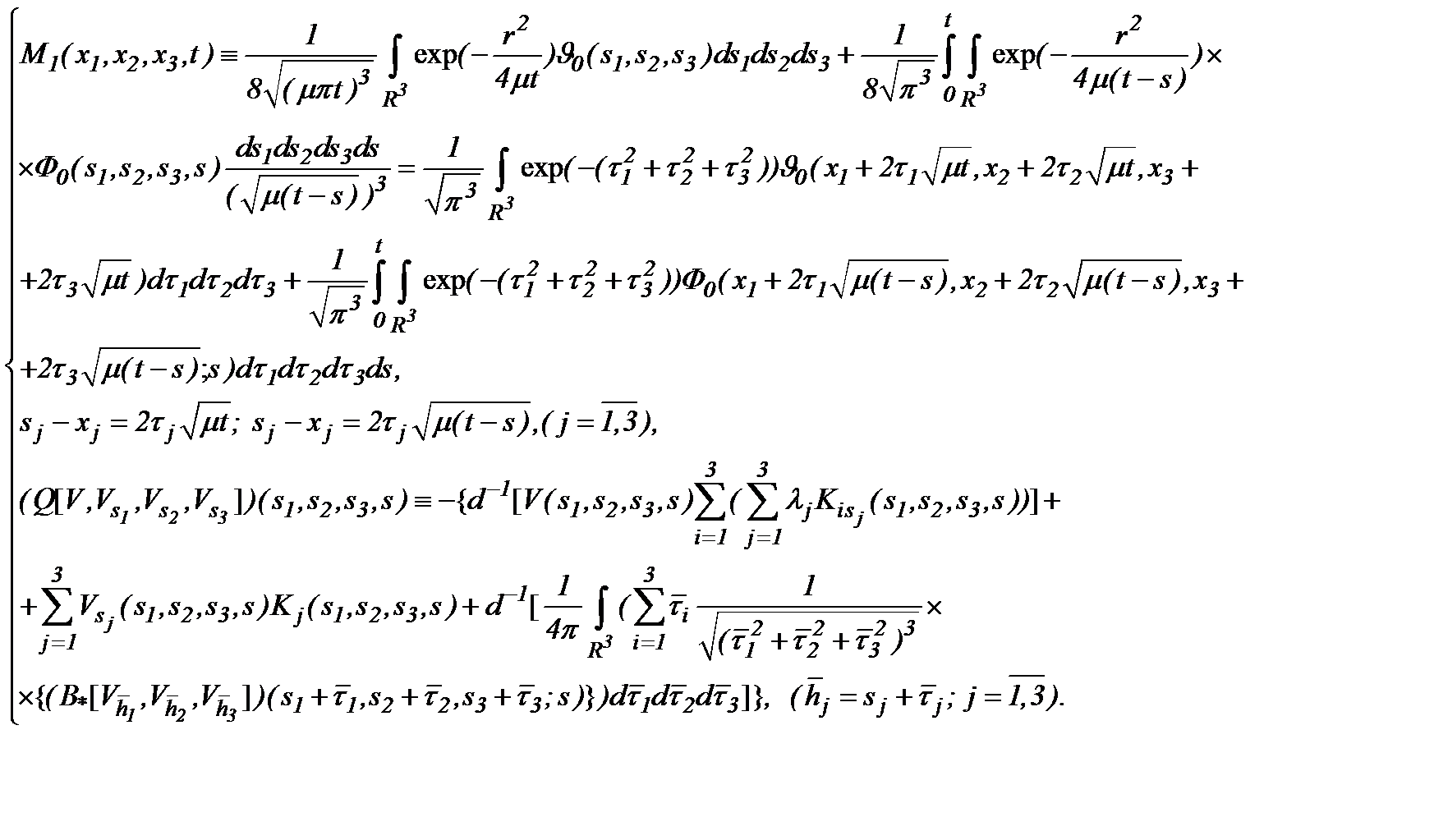
Уравнения (5.7) содержат неизвестные функции 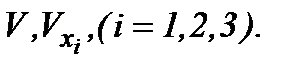 Дифференцируя (5.7) по
Дифференцируя (5.7) по 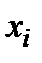 и вводя обозначение
и вводя обозначение
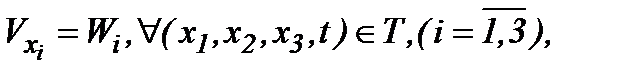 (5.8)
(5.8)
преобразуем выражение (5.7) в систему
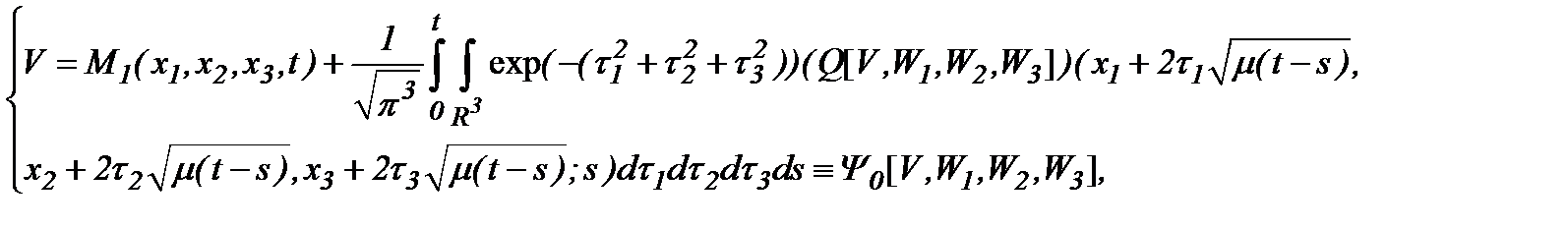
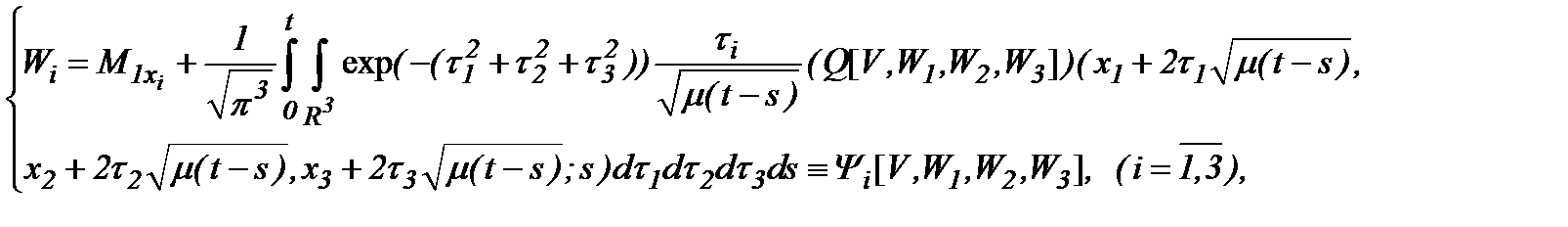 (5.9)
(5.9)
которая (5.9) состоит из четырех интегральных уравнений 2-го рода по переменной 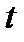 с четырьмя неизвестными функциями.
с четырьмя неизвестными функциями.
Для доказательства однозначной совместимости этой системы положим, что
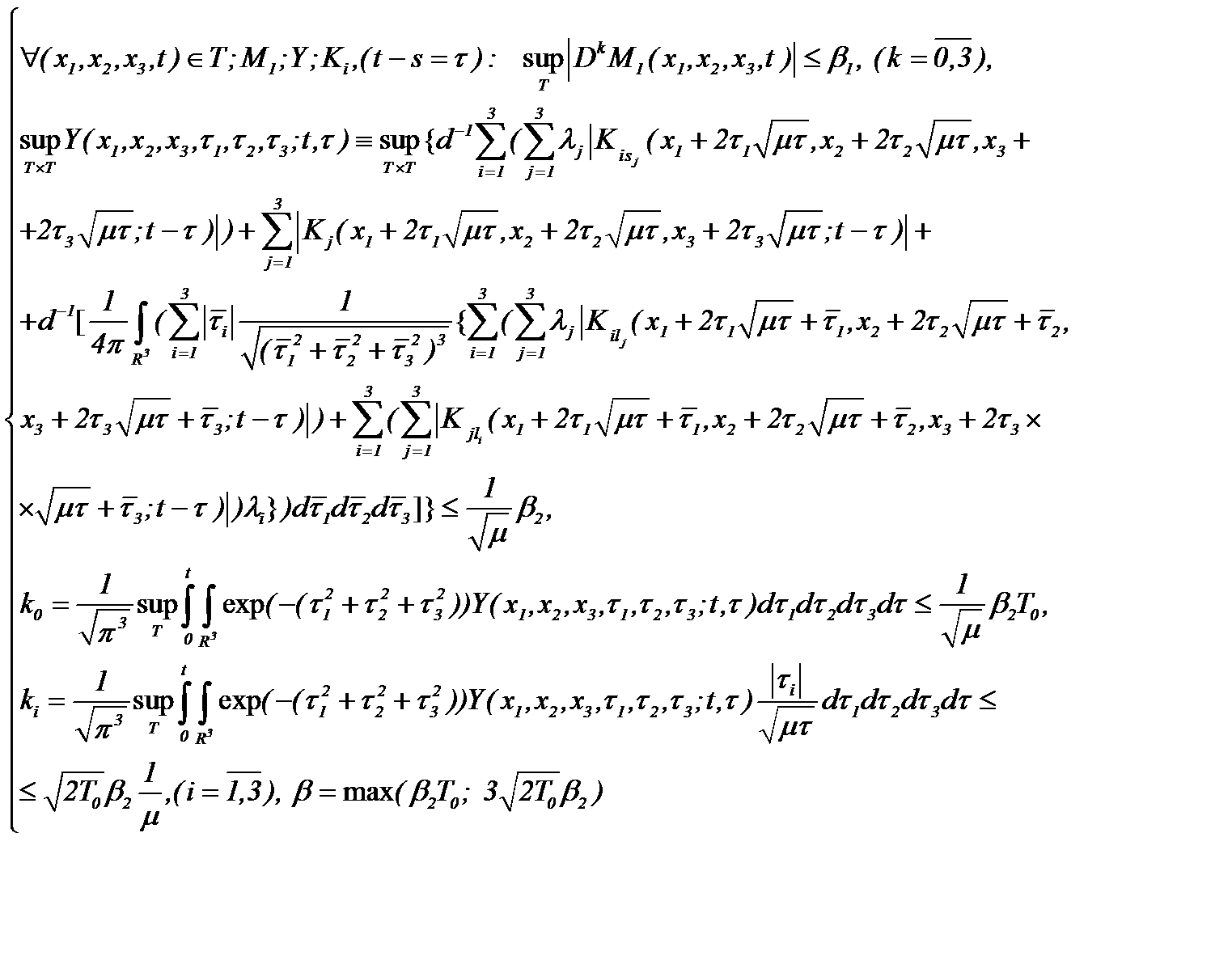 (5.10)
(5.10)
и
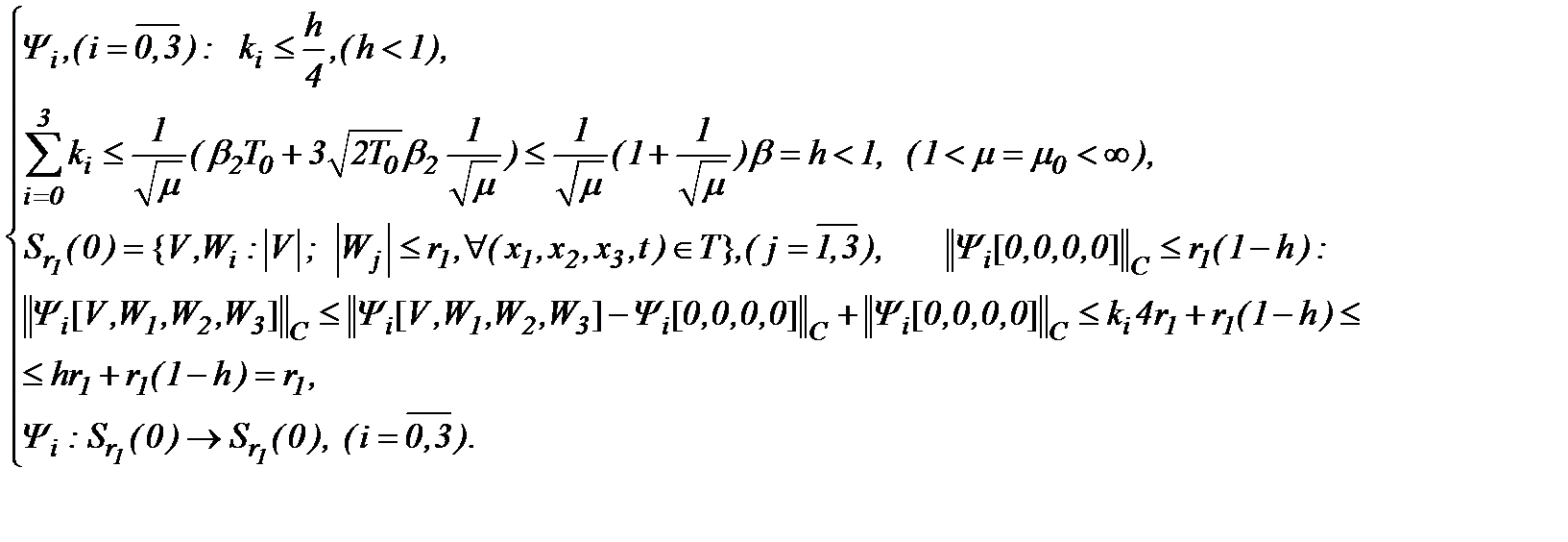 (5.11)
(5.11)
Тогда решение (5.9) существует и единственно и его можно найти по методу Пикара
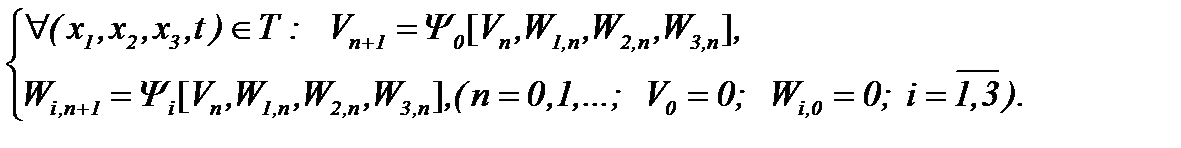 (5.12)
(5.12)
Поэтому на основе математических выводов метода Пикара последовательности функций 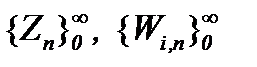 являются сходящимися и фундаментальными в
являются сходящимися и фундаментальными в 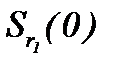 , при этом, то, что элементы построенных последовательностей принадлежат
, при этом, то, что элементы построенных последовательностей принадлежат 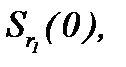 доказывается на основе выражения (5.11). Значит, последовательности
доказывается на основе выражения (5.11). Значит, последовательности 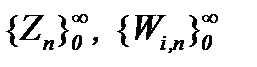 сходятся к пределу
сходятся к пределу 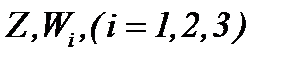 , т.е.
, т.е.
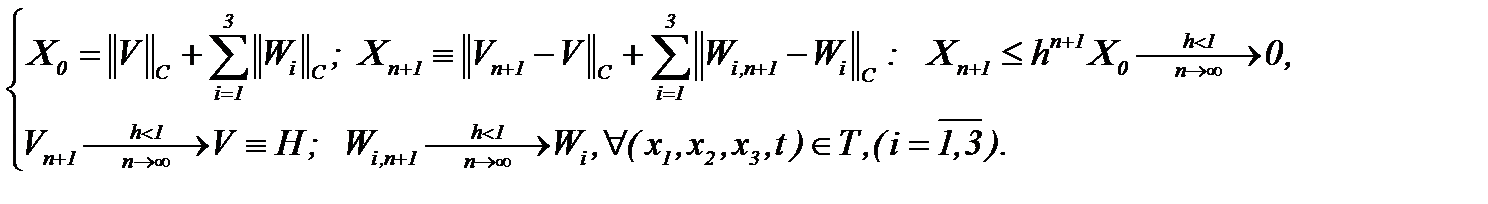 (5.13)
(5.13)
Тогда на основе правила (5.2), получим
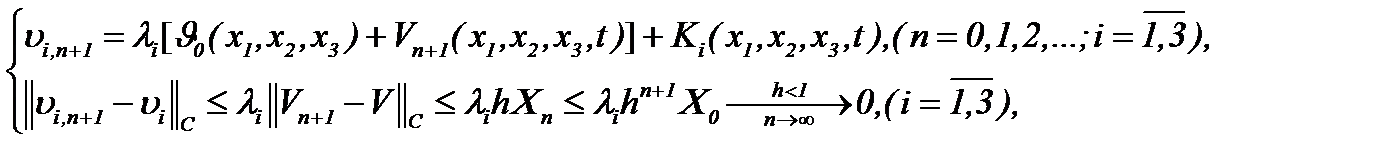 (5.14)
(5.14)
а это означает, что последовательности 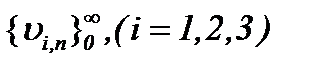 стремятся к пределу
стремятся к пределу 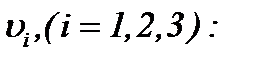
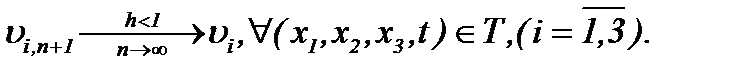 (5.15)
(5.15)
Теорема 6. Задача Навье-Стокса при условиях (1.2), (1.3), (5.1) и (5.15) имеет единственное непрерывное решение в 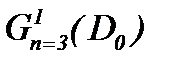 , которое определяется с помощью правила (5.2).
, которое определяется с помощью правила (5.2).
Замечания:
I . Единственность очевидна на основе метода от противного. Результаты (5.13) с условиями (5.1), (5.10), (5.11) получены, когда гладкость функций до требуемого порядка требуется только по 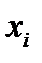 , так как производная первого порядка по времени определяется для всех
, так как производная первого порядка по времени определяется для всех 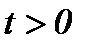 . Тогда с учетом (5.13) система (5.9) имеет единственное непрерывное решение, а потому уравнение (5.7) имеет единственное решение
. Тогда с учетом (5.13) система (5.9) имеет единственное непрерывное решение, а потому уравнение (5.7) имеет единственное решение 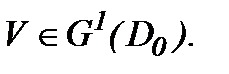 Значит, на основе (5.2), (5.14) и (5.15)
Значит, на основе (5.2), (5.14) и (5.15) 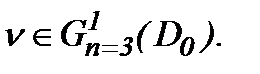
II . Алгоритм (5.2) также справедлив в случае, если
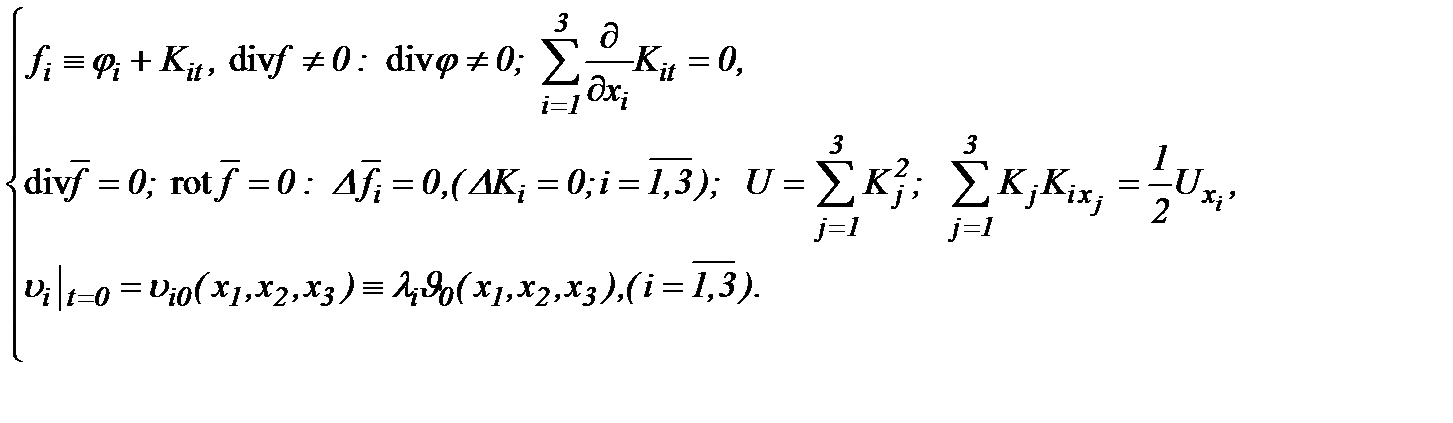 (5.16)
(5.16)
На основе (5.16) и (5.2) получим (5.4). Следовательно,
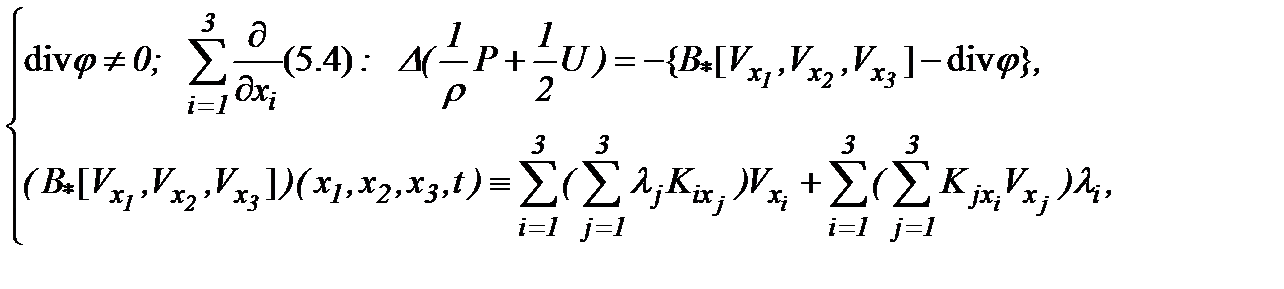
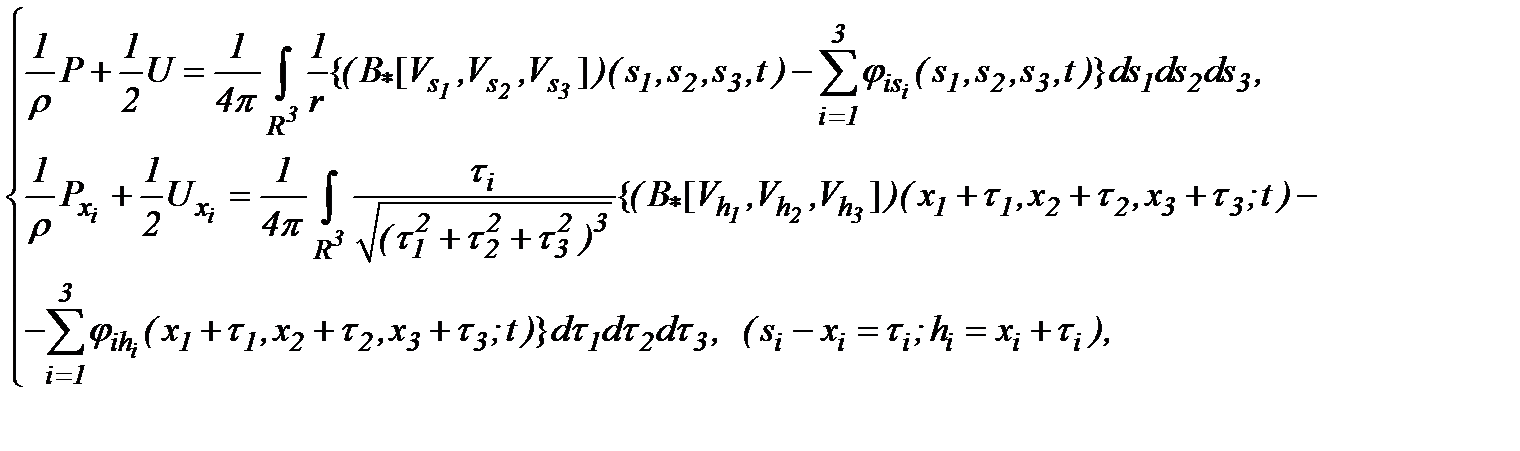 (5.17)
(5.17)
а поэтому имеет место
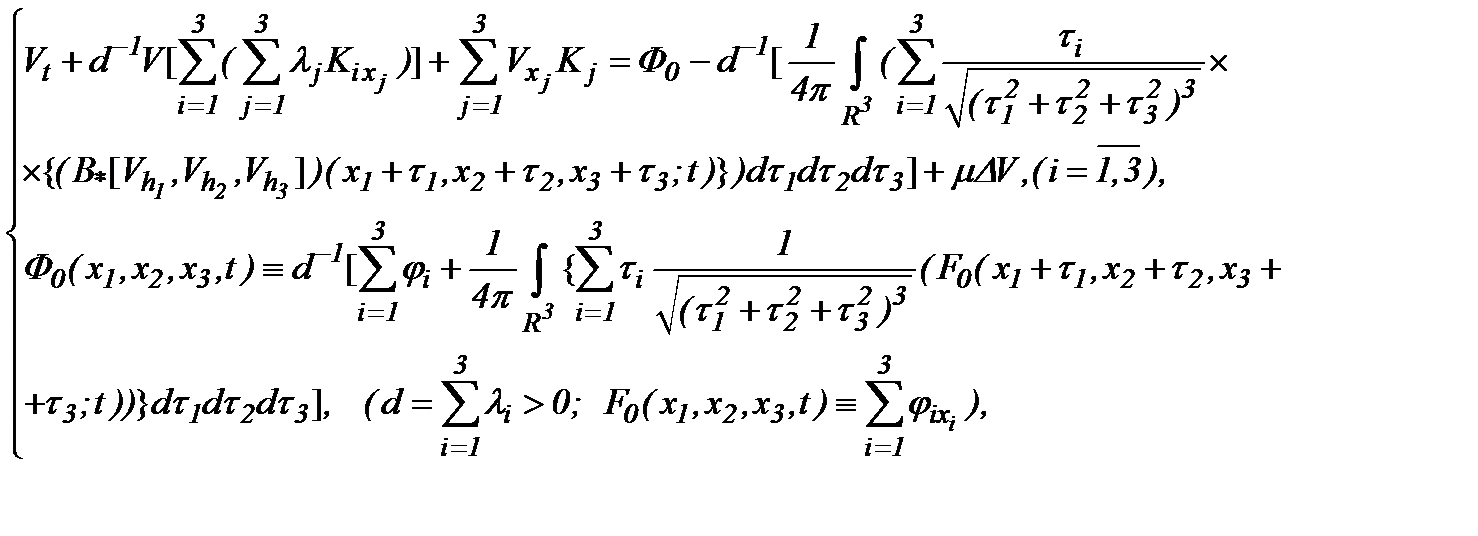 (5.18)
(5.18)
где выражение (5.17), как видно, отличается от (5.5), так как 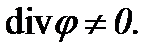
Тогда с учетом (5.18), (5.7) и (5.8), получаем систему (5.9)
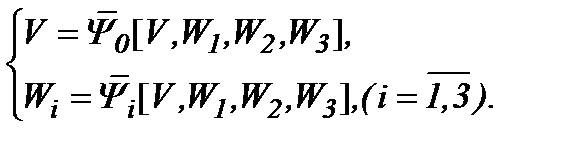 (5.19)
(5.19)
Относительно трансформированной системы (5.19), требуя выполнения условий (5.10), (5.11), (5.13), как следствие (5.14), получим
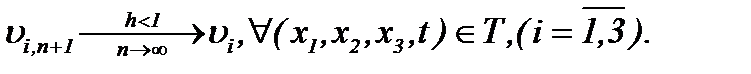 (5.20)
(5.20)
Значит, получен результат, аналогичный результату теоремы 6, что и требовалось доказать.








