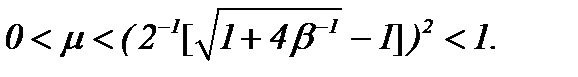Модифицированный вариант метода с условием
4.3. Модифицированный вариант метода (4.12) с условиями 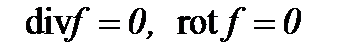
Новизна модификации метода (4.12) по пункту 4.3 в том, что компоненты скорости определяются более произвольно, чем в правилах (4.2) или (4.12), когда 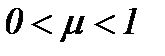 , а точнее с помощью регулирующих функций
, а точнее с помощью регулирующих функций 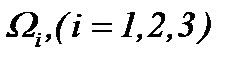 , причем, не теряя физическую значимость, а в этом выражается актуальность исследования при условиях
, причем, не теряя физическую значимость, а в этом выражается актуальность исследования при условиях 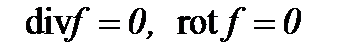 .
.
Предлагаемые методы интегральных преобразований вводятся так, чтобы преобразовать нелинейную задачу Навье-Стокса в линейную задачу теплопроводности. Разрешимость задач доказана на основе разработанных методов, так как они сводят начальные задачи к интегральным уравнениям Вольтерра-Абеля, где есть возможность найти аналитическое решение с учетом теории интегральных уравнений второго рода [13].
Для несжимаемых течений с трением, когда
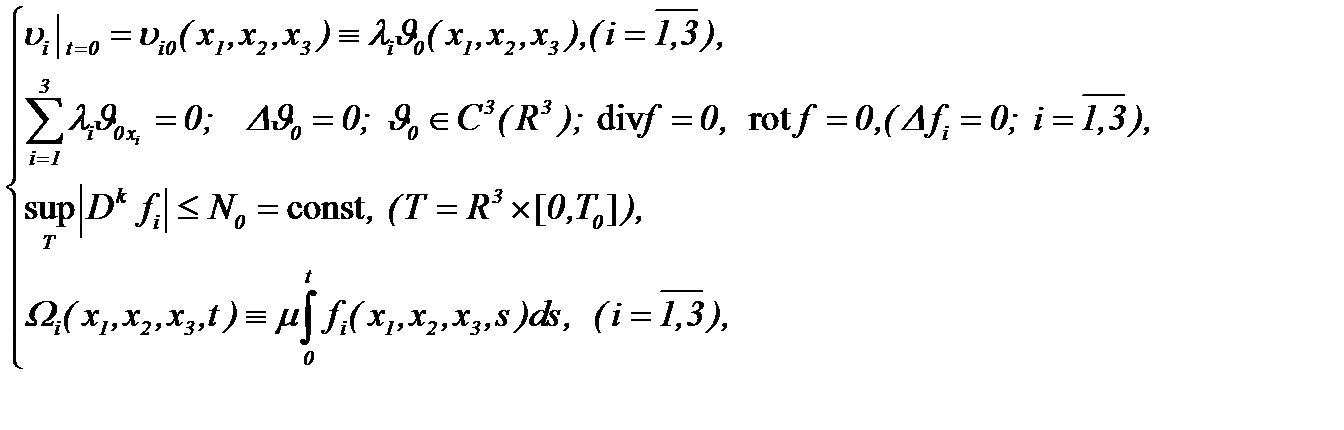 (4.21)
(4.21)
функции 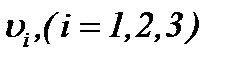 представимы в виде
представимы в виде
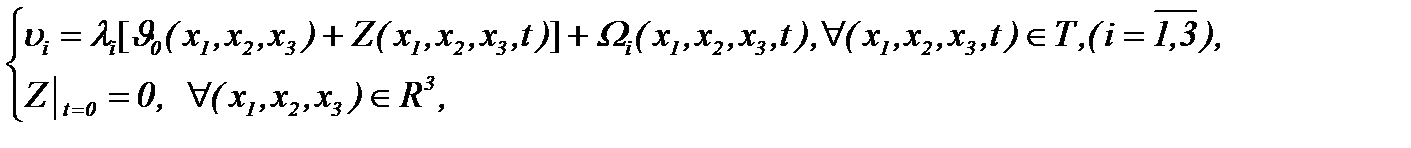 (4.22)
(4.22)
где 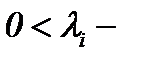 известные константы. От введенных функций
известные константы. От введенных функций 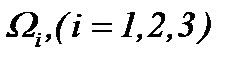 требуется, чтобы
требуется, чтобы
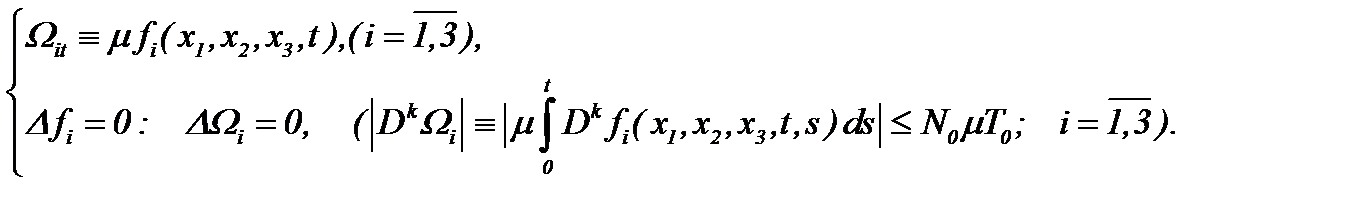
Причем, функции 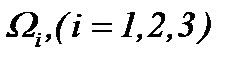 регулярны, относительно параметра вязкости в
регулярны, относительно параметра вязкости в 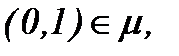 но поскольку вязкость
но поскольку вязкость 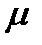 выступает в роли малого параметра, то
выступает в роли малого параметра, то
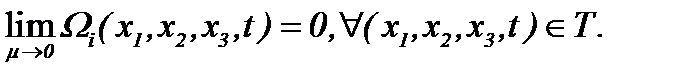
Кроме того, если предположить соблюдение (4.21), (4.22) и
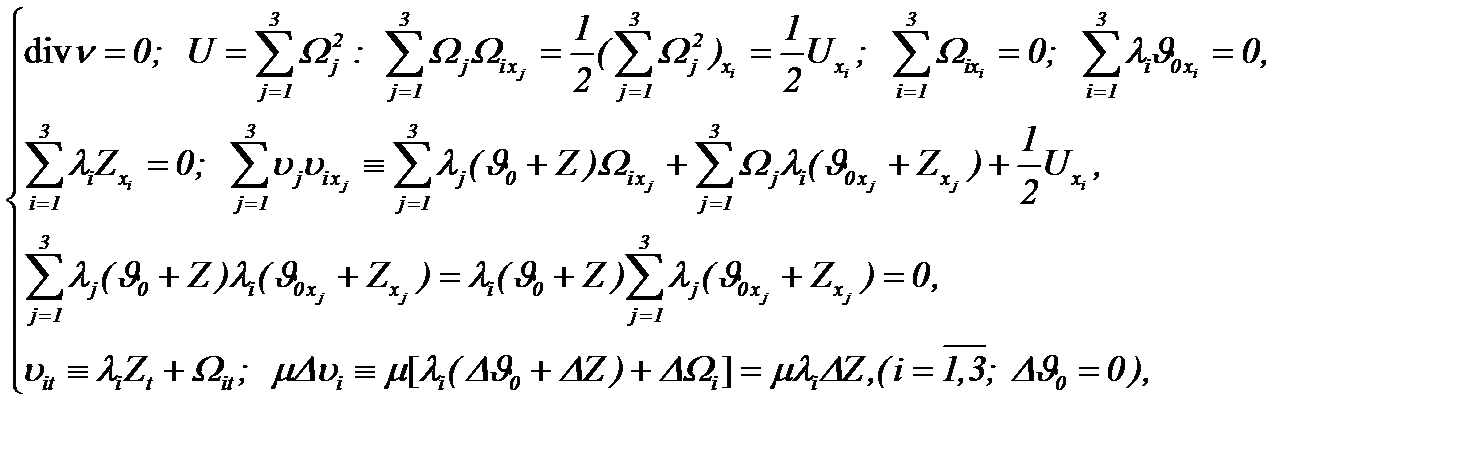 (4.23)
(4.23)
то уравнения Навье-Стокса (1.1) на основе (4.22) преобразуется к виду
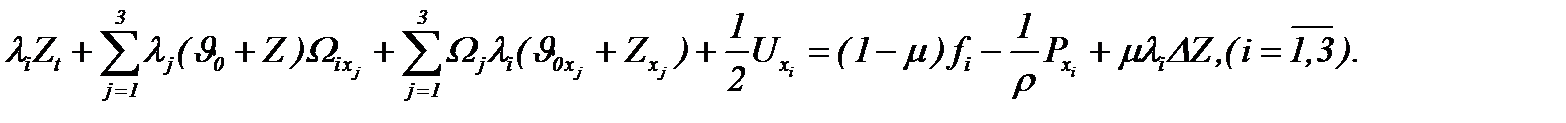 (4.24)
(4.24)
Системы (1.1) и (4.24) эквивалентны. Тогда новая система уравнений будет неоднородной линейной системой переноса вихрей [12]. Здесь инерционные члены в уравнениях (1.1) линеаризуются с помощью регулирующих функций 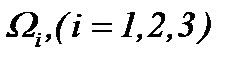 , которые были впервые введены в работе [8] и в методе (4.22).
, которые были впервые введены в работе [8] и в методе (4.22).
Из системы (4.24) с учетом условий (4.21) – (4.23), применяя АПС, получаем уравнение
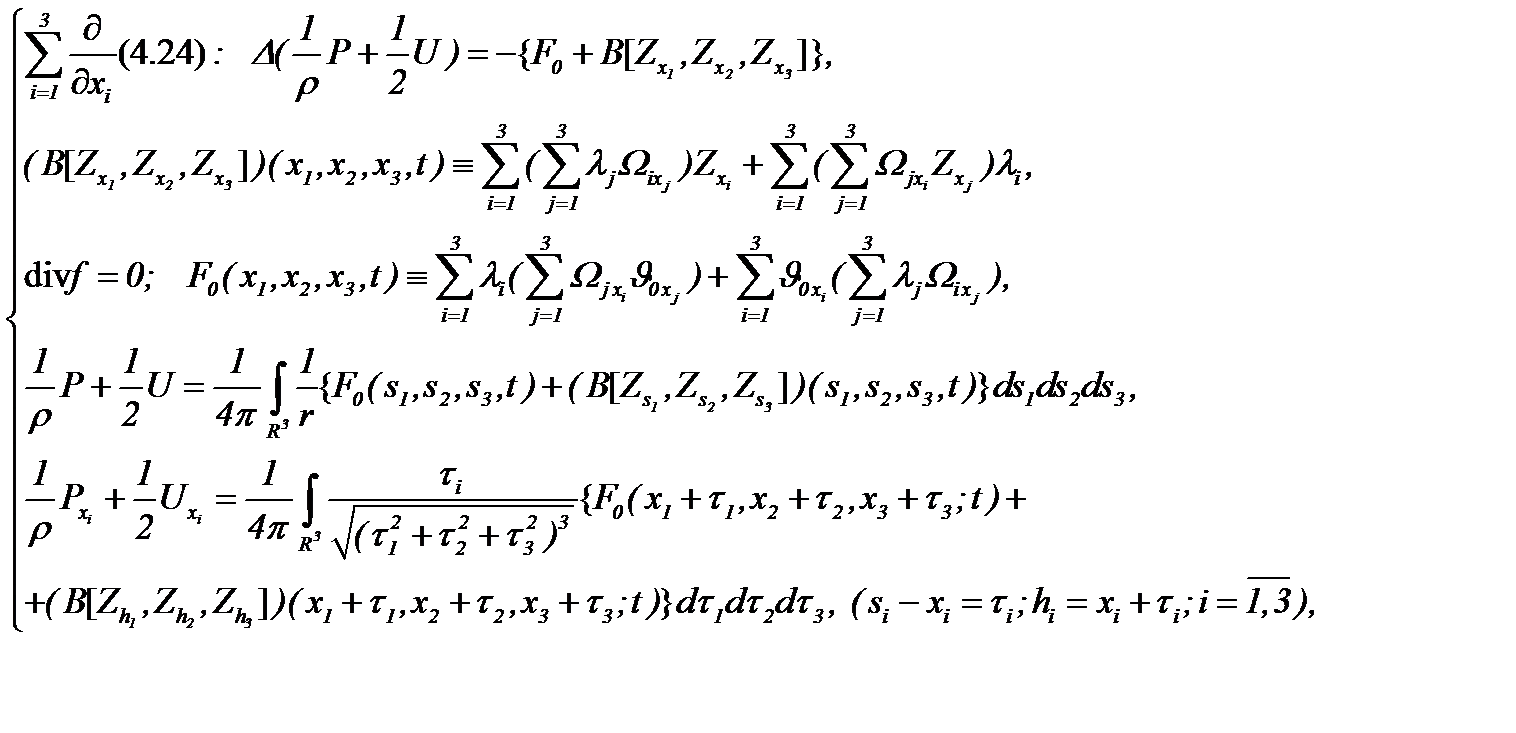 (4.25)
(4.25)
так как соблюдены условия
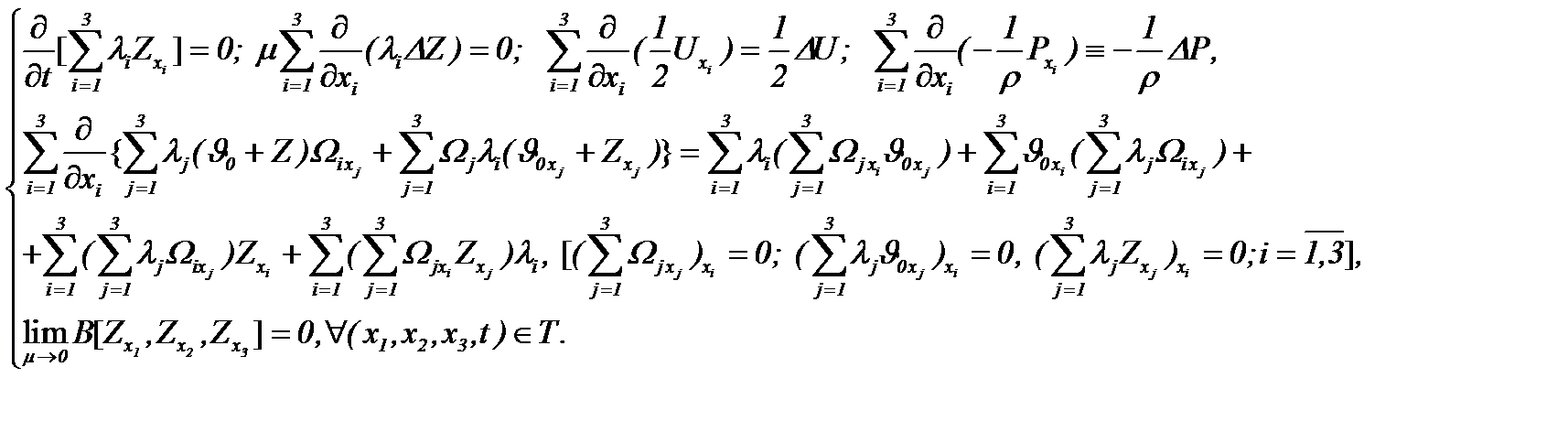
Существуют различные методы [12], которые дают связь скорости и давления в виде закона распределения давления, например, соотношение типа Бернулли. В данном пункте получен закон распределения давления в виде (4.25), но впервые такого рода результаты получены в работе [8]. Поэтому на основе закона (4.25) эквивалентно преобразуем систему (4.24) к виду
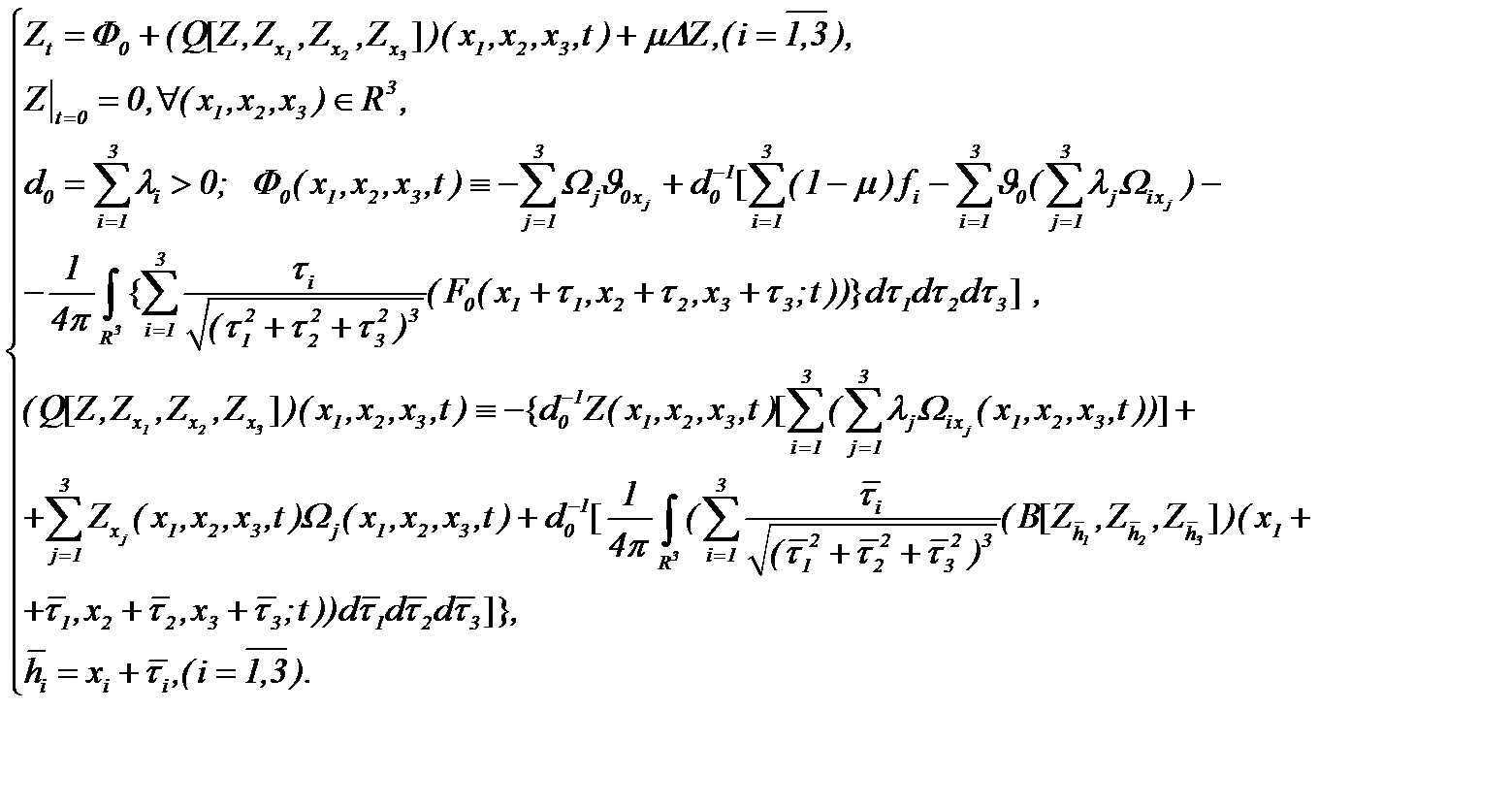 (4.26)
(4.26)
Тогда задача (4.26) трансформируется в систему интегральных уравнений, вполне регулярную относительно параметра вязкости 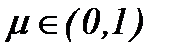 , и имеет следующий вид
, и имеет следующий вид
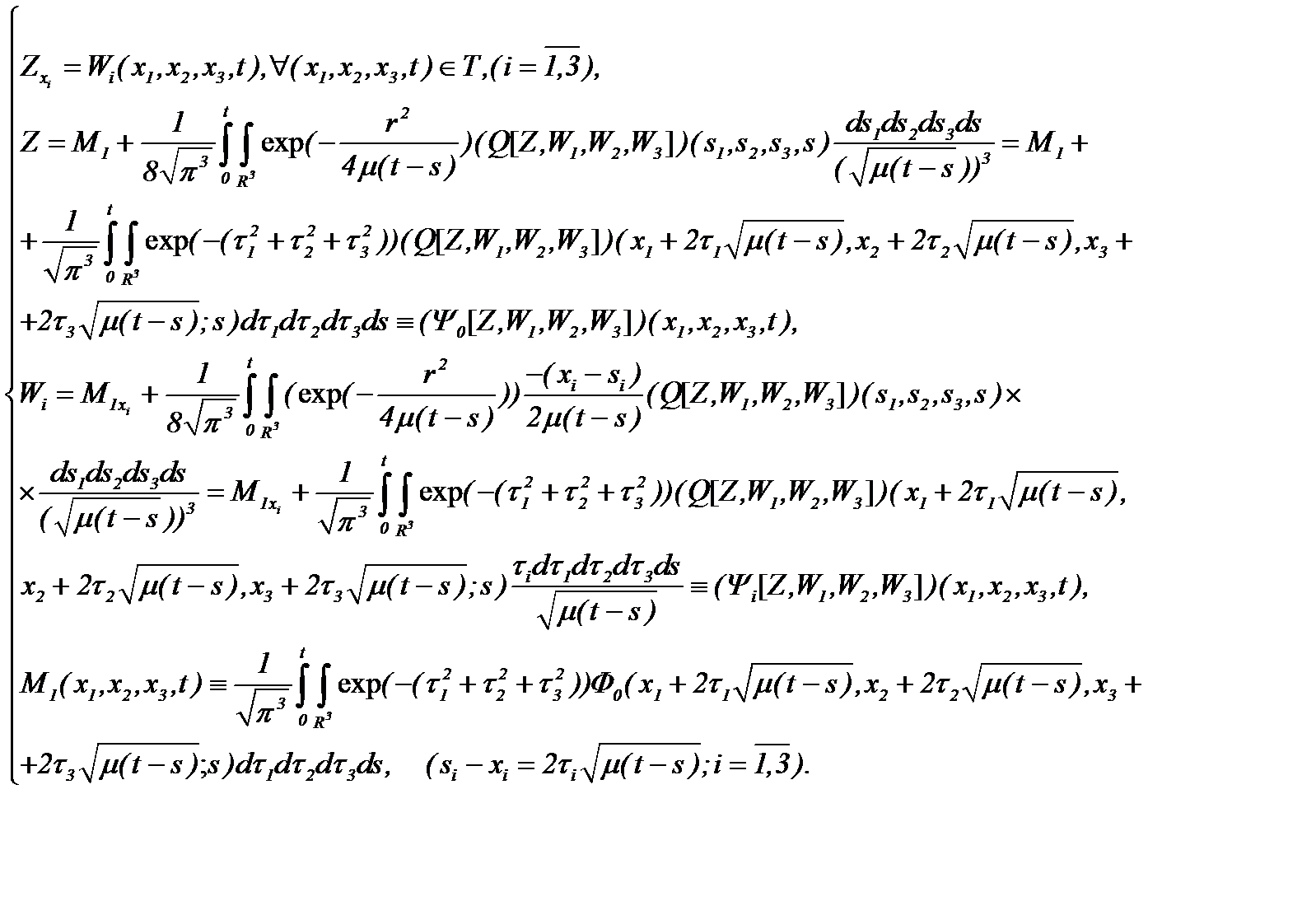 (4.27)
(4.27)
Полученная система (4.27) состоит из четырех интегральных уравнений Вольтерра и Вольтерра-Абеля 2-го рода по переменной 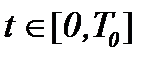 и содержит четыре неизвестные функции. Значит, для разрешимости системы (4.27) достаточно показать, каким образом обеспечивается принцип сжимающих отображений и становится возможным использовать метод Пикара для решения этой системы.
и содержит четыре неизвестные функции. Значит, для разрешимости системы (4.27) достаточно показать, каким образом обеспечивается принцип сжимающих отображений и становится возможным использовать метод Пикара для решения этой системы.
Итак, пусть имеет место
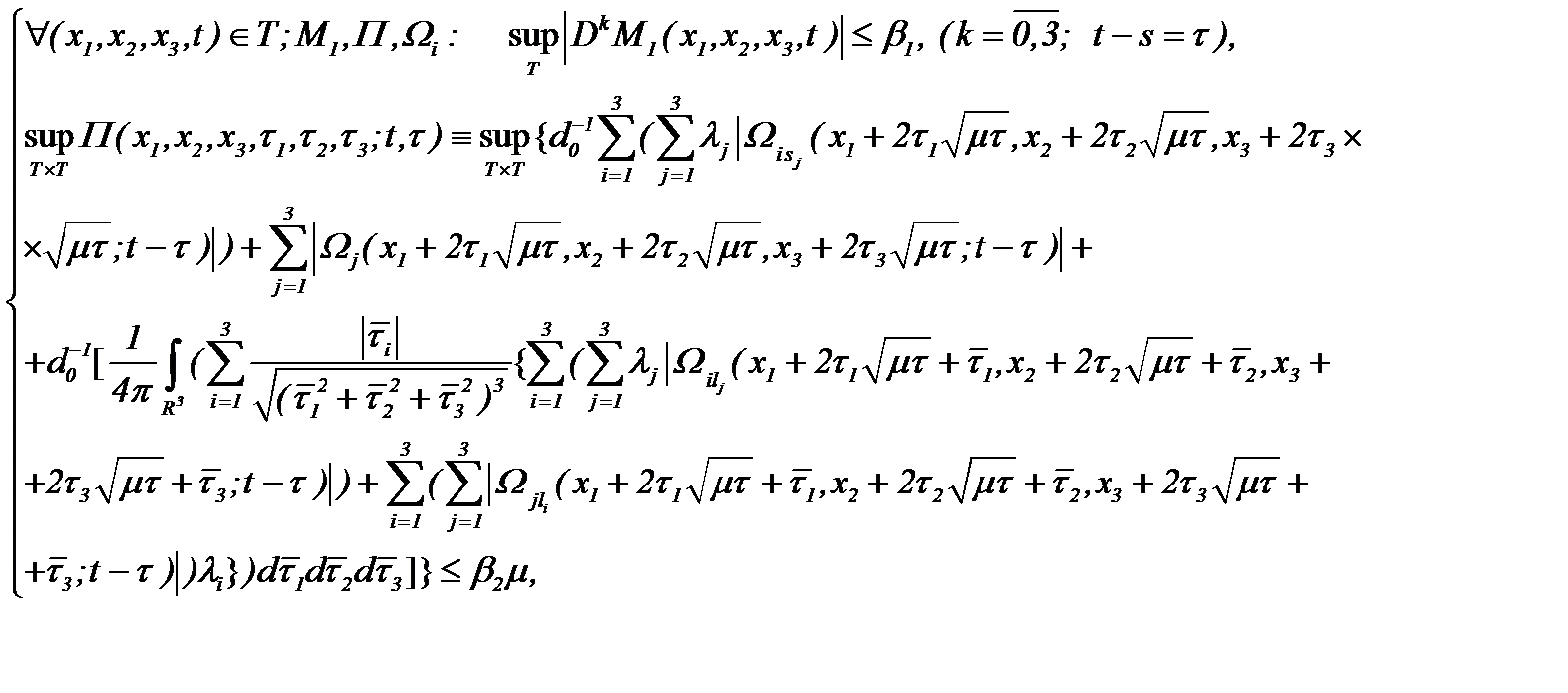
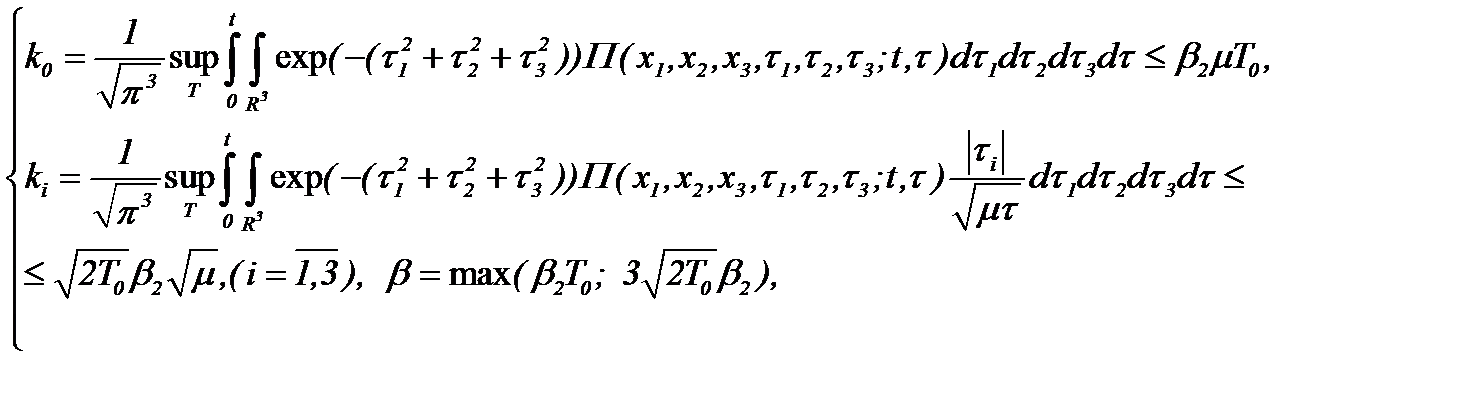 (4.28)
(4.28)
причем операторы 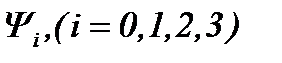 допускают сжатие отображений, т.е.
допускают сжатие отображений, т.е.
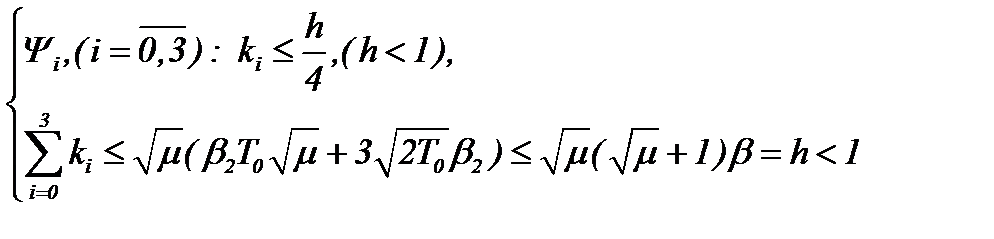 (4.29)
(4.29)
и
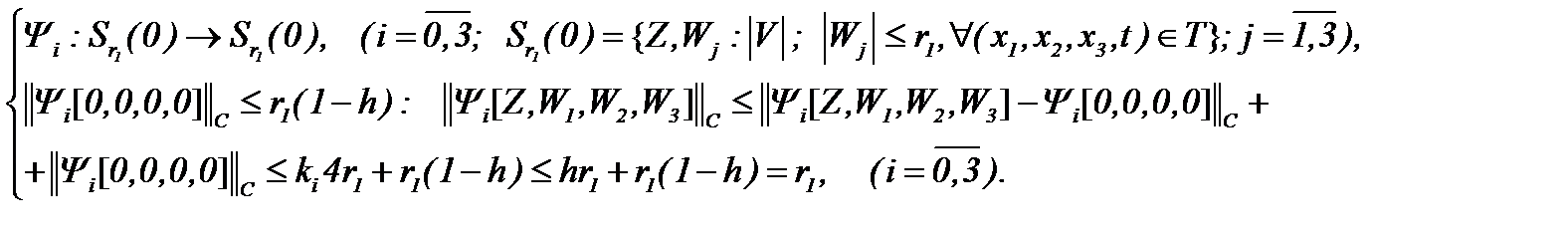 (4.30)
(4.30)
Тогда система (4.27) разрешима на основе принципа сжимающих отображений, а решение этой системы можно найти на основе метода Пикара
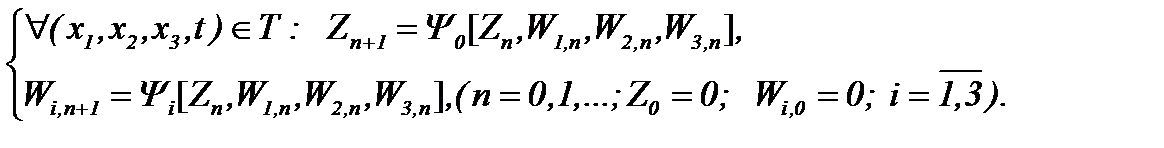 (4.31)
(4.31)
Исходя из чего, учитывая выводы метода последовательных приближений, находим, что построенные последовательности функции по правилу (4.31): 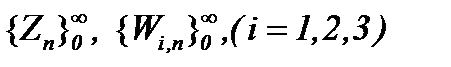 являются сходящимися и фундаментальными в
являются сходящимися и фундаментальными в 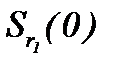 , причем, элементы построенных последовательностей принадлежат
, причем, элементы построенных последовательностей принадлежат 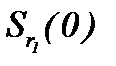 для
для 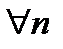 , так как имеют место
, так как имеют место
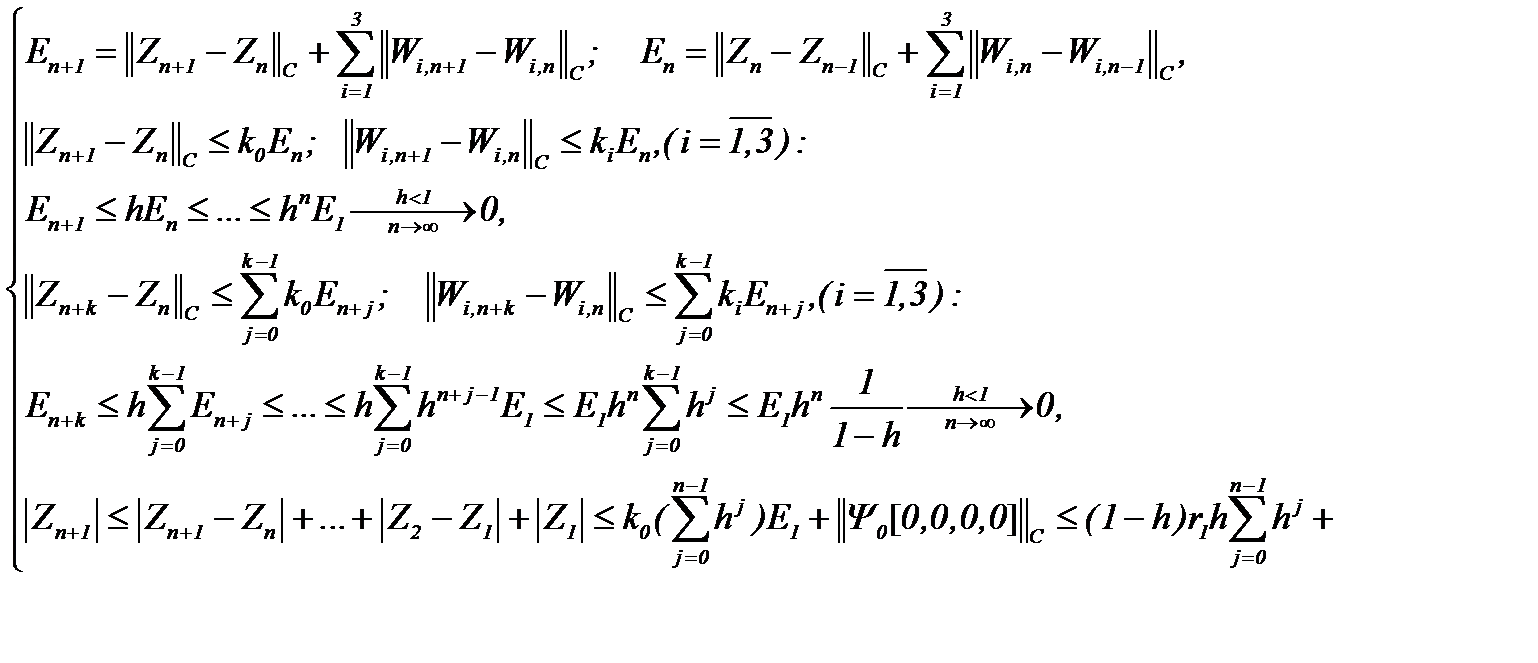
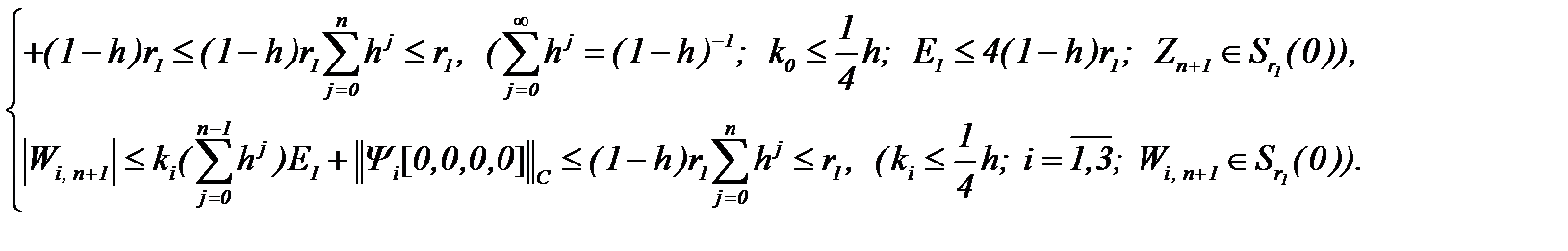 (4.32)
(4.32)
Значит, последовательности 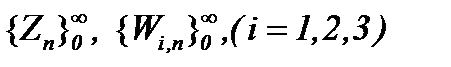 сходятся к пределу
сходятся к пределу 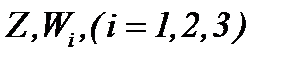 :
:
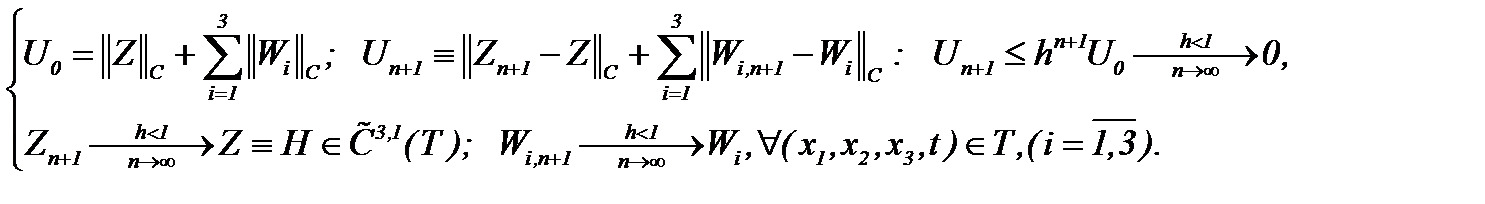 (4.33)
(4.33)
Тогда на основании (4.22) получим
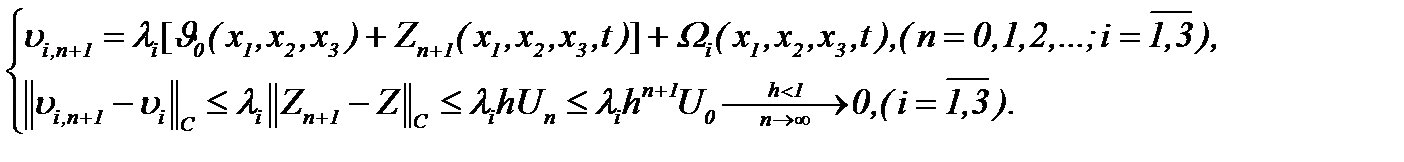 (4.34)
(4.34)
Отсюда следует, что последовательность функций 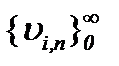 сходится к пределу
сходится к пределу 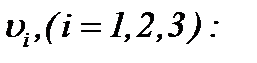
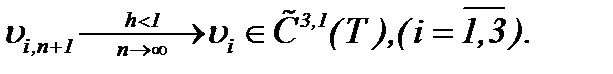 (4.35)
(4.35)
Теорема 5*. Задача Навье-Стокса при условиях (1.2), (1.3), (4.21), (4.22), (4.28) – (4.30) и (4.35) разрешима в 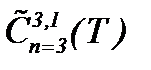 .
.
Замечание 4. Когда 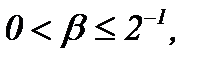 то
то 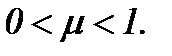 Если
Если 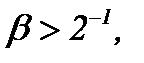 то
то 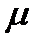 подчиняется неравенству
подчиняется неравенству