Существование, Единственность и Гладкость Решения Задачи Навье-Стокса для Несжимаемой Жидкости с Вязкостью
Таалайбек Д. Омуров
Доктор физ.-мат.наук, профессор Кыргызского национального университета им. Ж. Басалагуна, Бишкек, Кыргызстан, E-mail: omurovtd@mail.ru
Аннотация. Доказательство существования, единственности и гладкости (или условной гладкости) решения уравнений Навье-Стокса стало важнейшей математической проблемой тысячелетия: "Navier-Stokes Millennium Problem". Проблема ограничена изучением уравнений Навье-Стокса для вязкой несжимаемой жидкости. В данной работе разработаны методы построения аналитически гладких решений нестационарной задачи Навье-Стокса, представляющей собой указанную проблему тысячелетия [1].
Ключевые слова: шестая проблема тысячелетия, уравнения Навье-Стокса и Эйлера, критическое число Рейнольдса, критерий Билла-Като-Мажда
Предисловие
Исследование посвящено разработке методов решения 3D и nD уравнений Навье-Стокса, описывающих течение вязкой несжимаемой жидкости и включающее требования "Navier-Stokes Millennium Problem", так как разработанные методы решения содержат доказательство существования и гладкости (условной гладкости) решения уравнений Навье-Стокса, где ламинарное течение отделено от турбулентного течения, когда критическое число Рейнольдса Re = 2300. Решение получено для скорости и давления в аналитическом виде, как того требует Математический Институт Клея в постановке "Navier-Stokes Millennium Problem" [1]. Методы решения подкреплены примерами для различных интервалов вязкости, отвечающих прикладным задачам.
В параграфах 4.3, 4.4, 5, 6 и 7.3 найден новый закон распределения давления. Этот закон получен из уравнения пуассоновского типа и отличается от известных законов Бернулли, Дарси и др. Автор впервые применил специальные пространства для исследования существования и гладкости (в том числе, условной гладкости) уравнений Навье-Стокса для вязкой несжимаемой жидкости. В дальнейшем эти пространства можно назвать пространствами Омурова:
а) одно из них в случае гладкости – это пространство с нормами типа Чебышева,
б) другие имеют место в случае условной гладкости, например: 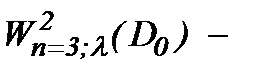 это весовое пространство с топологией типа Соболева.
это весовое пространство с топологией типа Соболева.
Академик К. Жумалиев, директор Института физики НАН КР
1 августа 2014 г.
1. Введение
Трудность решения 3D и nD уравнений Навье-Стокса обусловлена их нелинейностью и необходимостью найти скорость и давление в зависимости от любых значений параметра вязкости [1].
Обозначим компоненты векторов скорости и внешней силы, как
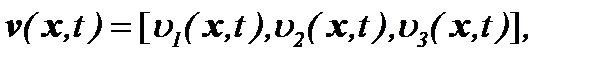
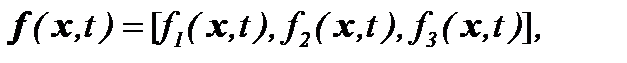
тогда соответствующая задача Навье-Стокса представима в виде
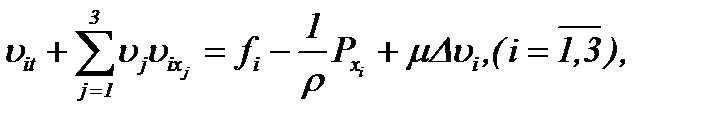 (1.1)
(1.1)
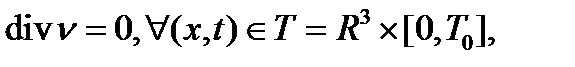 (1.2)
(1.2)
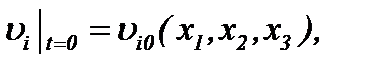
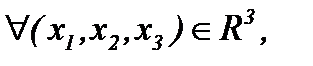 (1.3)
(1.3)
где 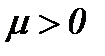 – кинематическая вязкость, r – плотность, D – оператор Лапласа. Условие несжимаемости жидкости (1.2) является дополнительным уравнением задачи (1.1) – (1.3), а скорость n и давление P – это неизвестные величины, подлежащие определению.
– кинематическая вязкость, r – плотность, D – оператор Лапласа. Условие несжимаемости жидкости (1.2) является дополнительным уравнением задачи (1.1) – (1.3), а скорость n и давление P – это неизвестные величины, подлежащие определению.
Для решения поставленной задачи (1.1) – (1.3) предлагается трансформировать уравнения Навье-Стокса следующим образом. Преобразуем (1.1) к виду [7, 10]:
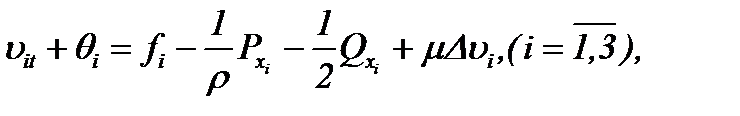 (1.4)
(1.4)
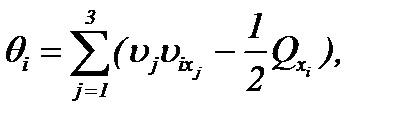 (1.5)
(1.5)
где
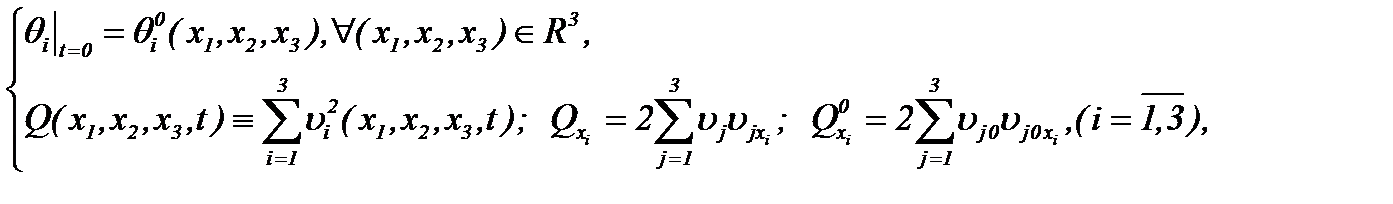
не нарушая, тем самым, эквивалентность системы (1.1) и (1.4), (1.5). Полученные системы (1.4), (1.5) содержат неизвестные функции 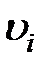 ,
, 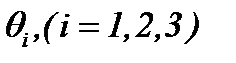 и давление P. Здесь
и давление P. Здесь 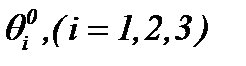 – известные функции, так как известны
– известные функции, так как известны 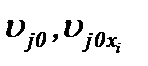 .
.
Предлагаемый метод решения систем (1.4) и (1.5) связан с функциями 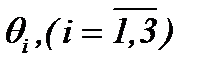 , а именно:
, а именно:
A1) 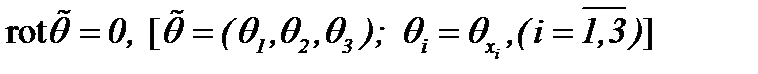 ;
; 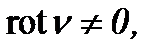 или
или
А2) 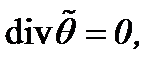
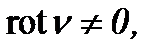 или
или
А3) 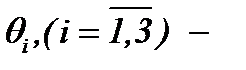 произвольные функции, если, соответственно выполняются как необходимые условия:
произвольные функции, если, соответственно выполняются как необходимые условия:
а01) 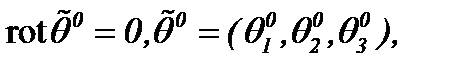 а02)
а02) 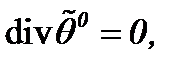 а03)
а03) 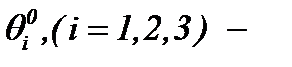 произвольные функции.
произвольные функции.
Известно, что решение многих проблем теоретической и математической физики требует применения специальных весовых пространств. В работах [7, 9] впервые предложен метод решения задачи Навье-Стокса в пространстве 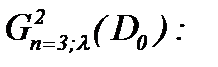
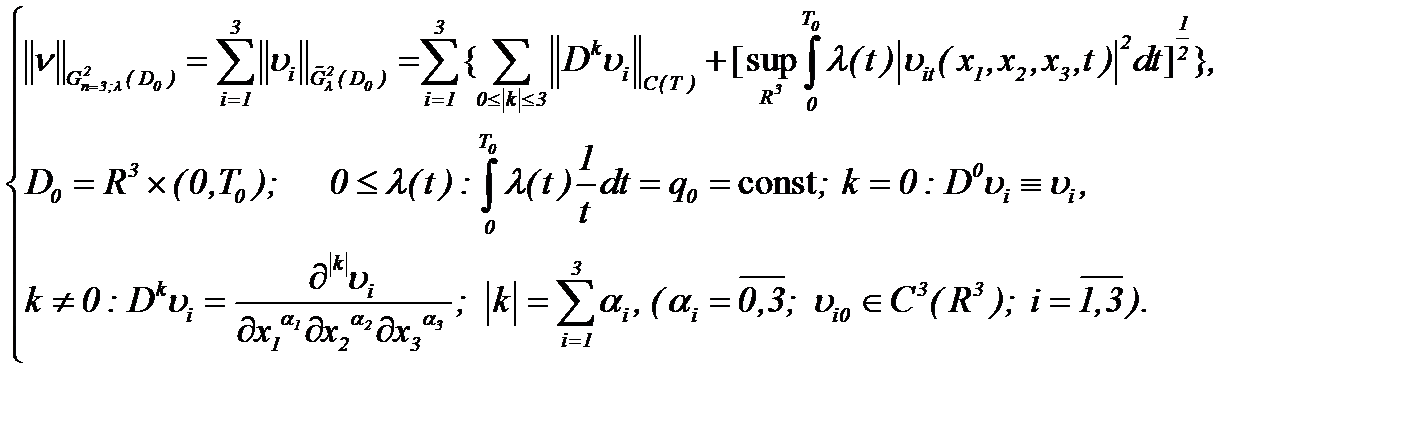 (1.61)
(1.61)
Как альтернатива, в работе [8] на основании леммы К. Фридрихса [15] был построен класс подходящих решений в 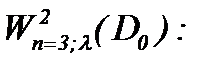
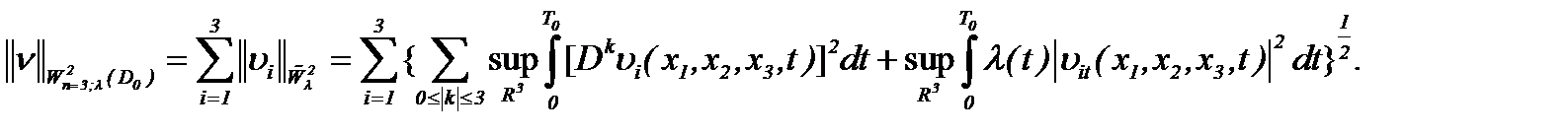 (1.62)
(1.62)
Цель работы. Основная цель настоящей работы – это доказательство существования, единственности и гладкости (или условной гладкости) решения задачи Навье-Стокса для несжимаемой жидкости с вязкостью. В случае гладкости решения результаты исследований получены в пространстве 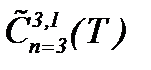 :
:
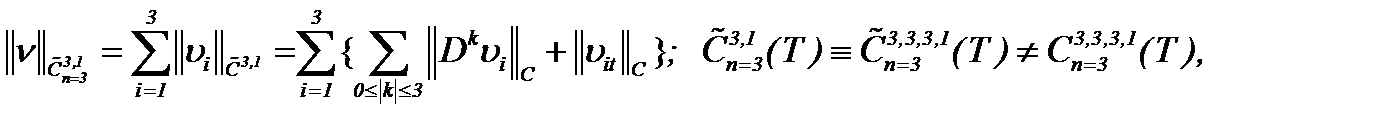 (1.63)
(1.63)
но в случае условной гладкости – в пространстве 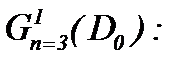
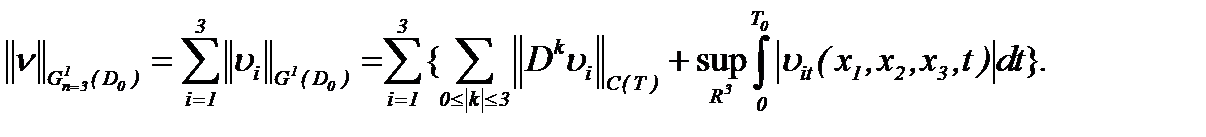 (1.64)
(1.64)
Так как 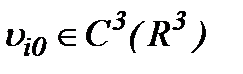 , то ограниченность решения задачи Навье-Стокса (1.1) – (1.3) можно доказать, как и в [8], в
, то ограниченность решения задачи Навье-Стокса (1.1) – (1.3) можно доказать, как и в [8], в 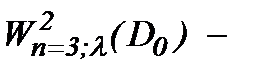 весовом пространстве типа Соболева.
весовом пространстве типа Соболева.
Известно, что из равномерной сходимости последовательности непрерывных функций на [a, b] следует сходимость в среднем на [a, b]. Поэтому, поскольку норма: 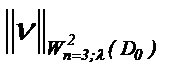 подчинена
подчинена 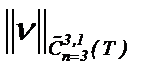 , то из сходимости последовательности
, то из сходимости последовательности 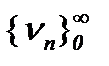 в смысле
в смысле 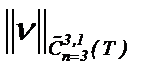 вытекает ее сходимость в
вытекает ее сходимость в 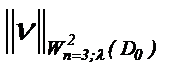 , причем к тому же самому элементу. Таким образом, если решение задачи (1.1) ограничено в пространстве
, причем к тому же самому элементу. Таким образом, если решение задачи (1.1) ограничено в пространстве 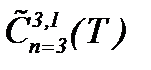 , то следует ограниченность в пространстве
, то следует ограниченность в пространстве 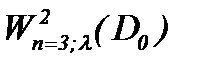 , обратное неверно.
, обратное неверно.
Научная ценность. Разработанные методы без привлечения дополнительных условий преобразуют задачу Навье-Стокса в неоднородные линейные уравнения типа теплопроводности с условием Коши, которые обладают теми же свойствами, что и решение задачи Коши для уравнений Навье-Стокса. В полученных уравнениях аналитическое решение регулярно в отношении фактора вязкости, что во многом упрощает анализ в математическом и физическом смысле [6, 11, 12].
Важным дополнением к решению явилось исследование жидкости с очень малой вязкостью, когда Re ≥ 2300. Оказалось, что и в этом случае разработанные методы дают аналитическое решение задачи Навье-Стокса для несжимаемой жидкости, чем позволяют достичь полного понимания физики турбулентности [4, 12].
Кроме того, в работе исследованы течения со средним размером вязкости при сохранении всех инерционных членов. Отметим, что в медленных течениях или в течениях со средней величиной вязкости, когда конвективное ускорение не равно нулю, возникали проблемы интегрирования уравнений Навье-Стокса в общем виде [12]. Поэтому полученные результаты работы отражают применимость метода к задаче Навье-Стокса со всевозможными значениями вязкости, а также, когда вязкость выступает в роли параметра, а потому доказывают значимость разработанных методов.
Далее, на основе разработанных методов аналогичные результаты получены и относительно задачи Навье-Стокса для несжимаемой жидкости с вязкостью, когда 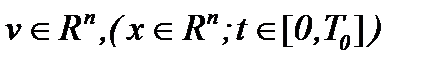 .
.
Вопросы физики и приложений уравнений Навье-Стокса здесь не рассматриваются, с ними можно ознакомиться в [3, 4, 6, 11, 12].
2. Жидкость с Очень Малой Вязкостью с Условием ( A 1 )
В этом параграфе при определенных ограничениях на входные данные будет дано строгое обоснование однозначной совместимости системы (1.4) – (1.5) для очень малой вязкости 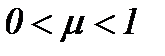 . В предельном случае весьма малых сил трения, т.е. для больших чисел Рейнольдса, решение уравнений Навье-Стокса обладают таким свойством, что все поле потока можно разделить на две области [12], где существует тонкий слой, в котором проявляет себя трение. Во внешней области поток не зависит от сил трения, свободен от вращения частиц, а потому описывается уравнениями Эйлера. Поэтому в этом параграфе изучается поведение решения уравнений Навье-Стокса, когда вязкость стремится к нулю.
. В предельном случае весьма малых сил трения, т.е. для больших чисел Рейнольдса, решение уравнений Навье-Стокса обладают таким свойством, что все поле потока можно разделить на две области [12], где существует тонкий слой, в котором проявляет себя трение. Во внешней области поток не зависит от сил трения, свободен от вращения частиц, а потому описывается уравнениями Эйлера. Поэтому в этом параграфе изучается поведение решения уравнений Навье-Стокса, когда вязкость стремится к нулю.
2.1. Жидкость с условием ( A 1 )
Пусть функции 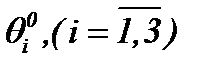 удовлетворяют условию (a01). Тогда относительно
удовлетворяют условию (a01). Тогда относительно 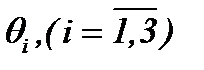 , предполагая условие (A1) и
, предполагая условие (A1) и
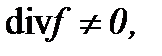 (2.1)
(2.1)
из системы (1.4) – (1.5), соответственно, получим следующие системы
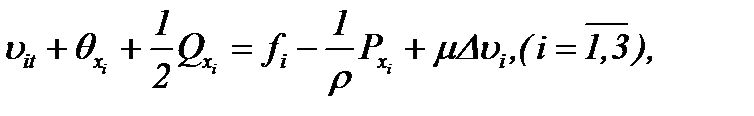 (2.2)
(2.2)
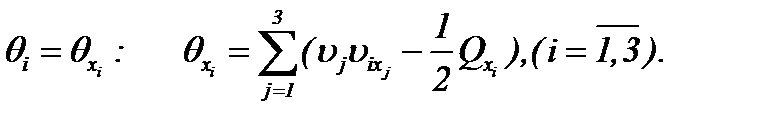 (2.3)
(2.3)
Теорема 1. Пусть выполнены условия (1.2), (1.3), (A1) и (2.1). Тогда системы (2.2) и (2.3) эквивалентно преобразуются к виду
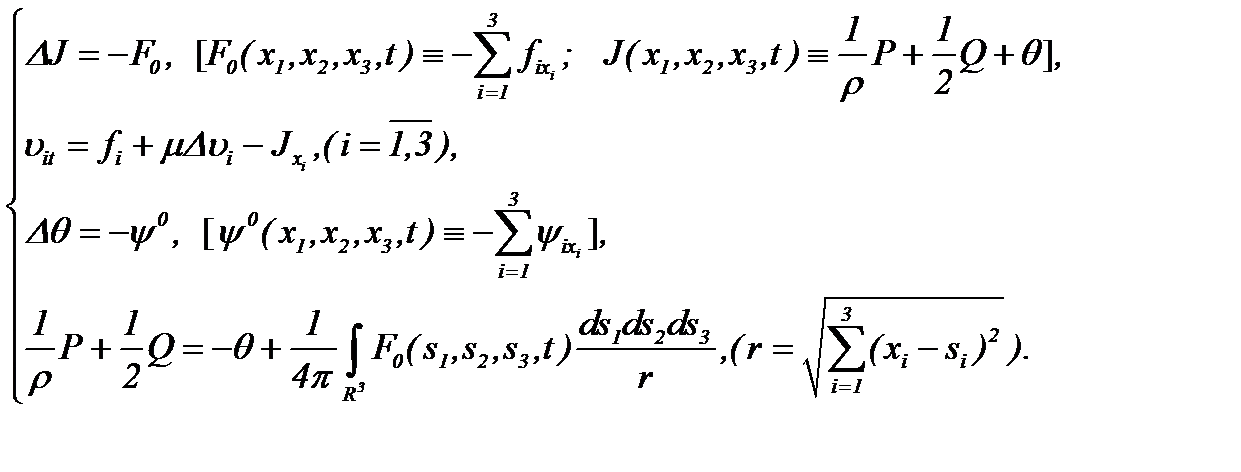 (2.4)
(2.4)
В таком случае задача (1.1) – (1.3) имеет единственное решение, удовлетворяющее условию (1.2).
Доказательство. Доказательство теоремы 1 состоит из четырех этапов.
1) Из системы (2.2) выведем следующий алгоритм [8]. На первом шаге считаем, что первое уравнение (2.2, i = 1) дифференцируемо по 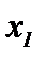 , второе уравнение (2.2, i = 2) – по
, второе уравнение (2.2, i = 2) – по 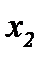 , третье (2.2, i = 3) – по
, третье (2.2, i = 3) – по 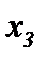 . На втором шаге, беря за основу формулу
. На втором шаге, беря за основу формулу
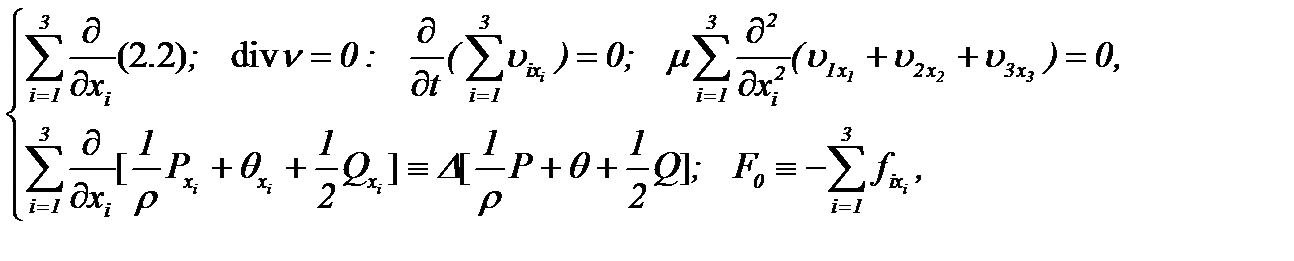 (2.5)
(2.5)
получим уравнение Пуассона [13]
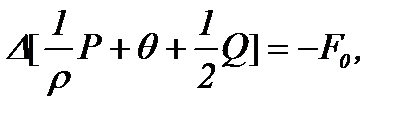
т.е.
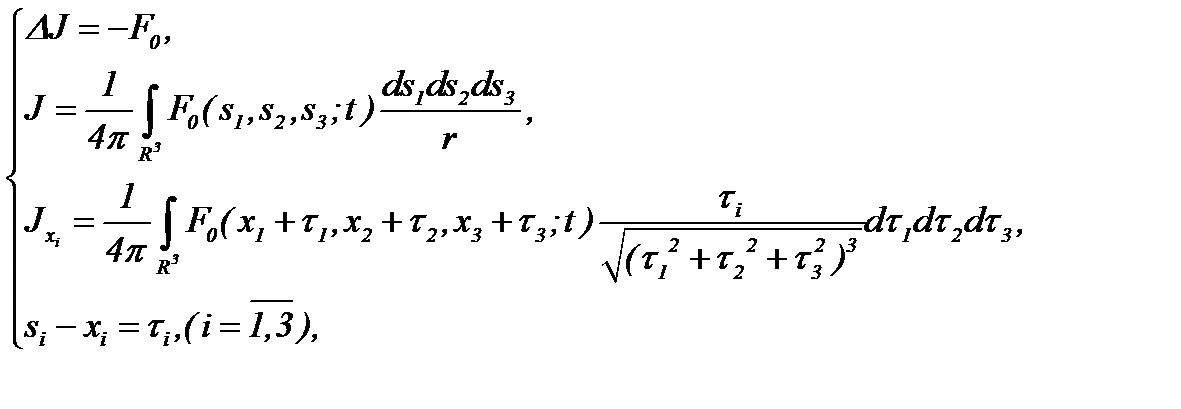 (2.6)
(2.6)
так как
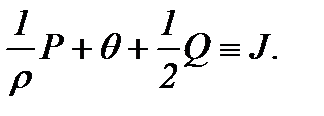 (2.7)
(2.7)
Алгоритм вывода уравнения Пуассона (2.6) назовем "алгоритмом пуассонизации системы", далее, для краткости АПС. Поэтому, если 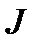 – решение уравнения (2.6), то подставляя в (2.2)
– решение уравнения (2.6), то подставляя в (2.2)
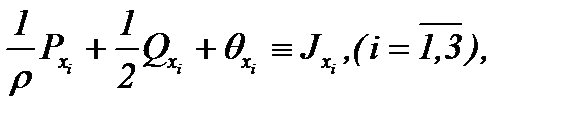 (2.8)
(2.8)
имеем
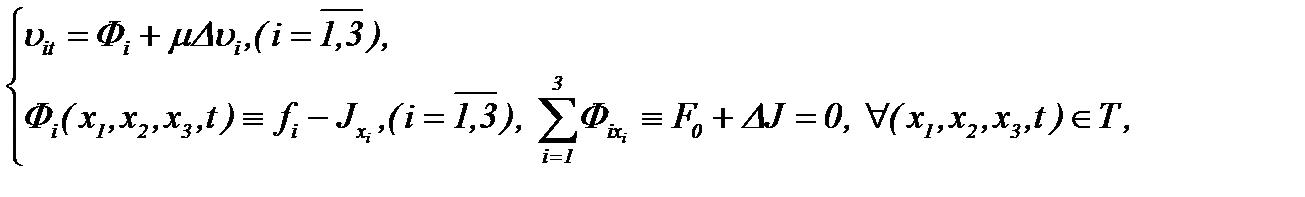 (2.9)
(2.9)
т.е. система (2.2) эквивалентна (2.9). Это означает, что уравнение (2.2) преобразовано в линейное неоднородное уравнение теплопроводности, где уравнения (2.6) и (2.9) – это соответственно первое и второе уравнения системы (2.4).
2) Из полученных результатов следует, что система (1.1) трансформируется в систему линейных уравнений теплопроводности с условием Коши. Значит, задача Коши с достаточно гладкими начальными данными при t = 0 разрешима в классе ограниченных функций [13, 14], поэтому задача Навье-Стокса имеет единственное условно-гладкое решение [8] в 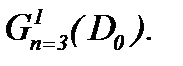
Действительно, из системы (2.9) следует
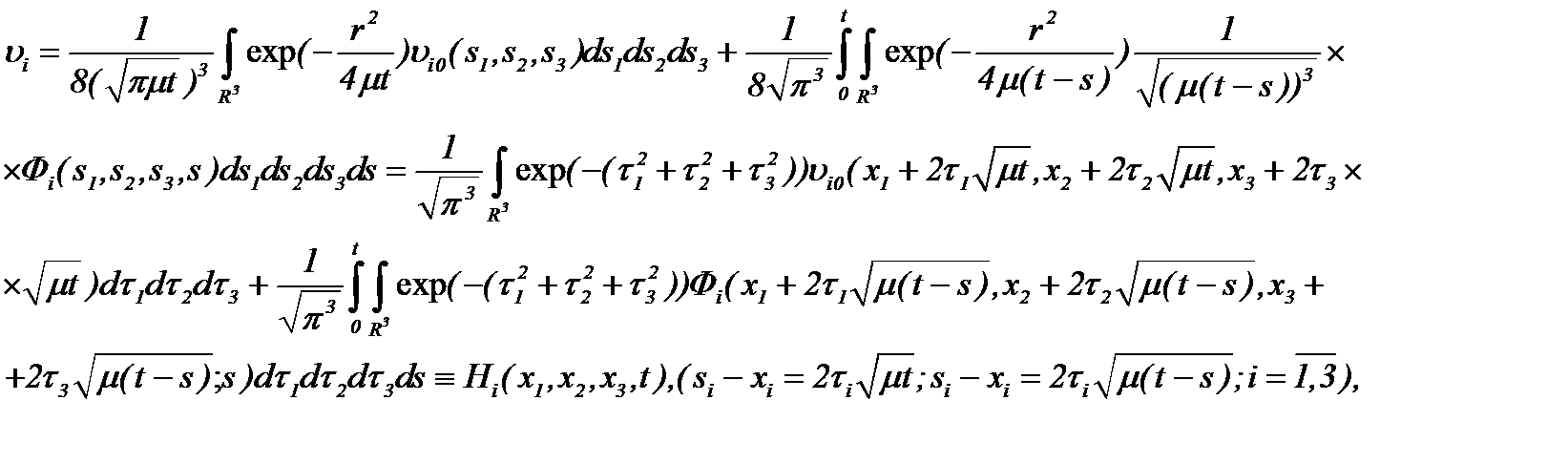 (2.10)
(2.10)
где Hi – известные функции. Найденное решение (2.10) удовлетворяет системе (2.9).
Для этого, с учетом частных производных системы (2.10):
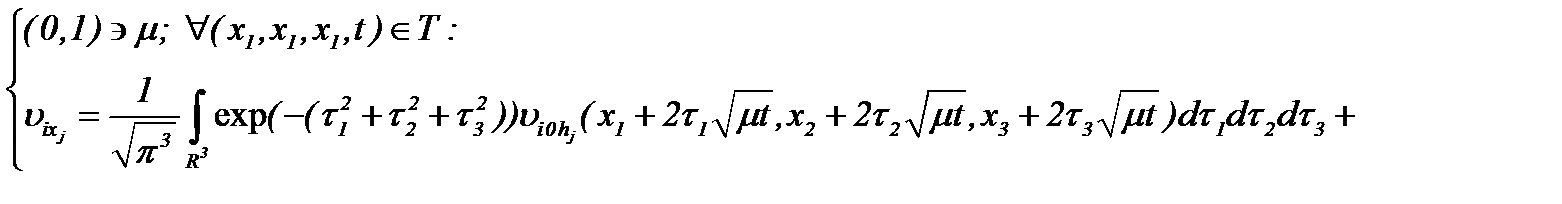
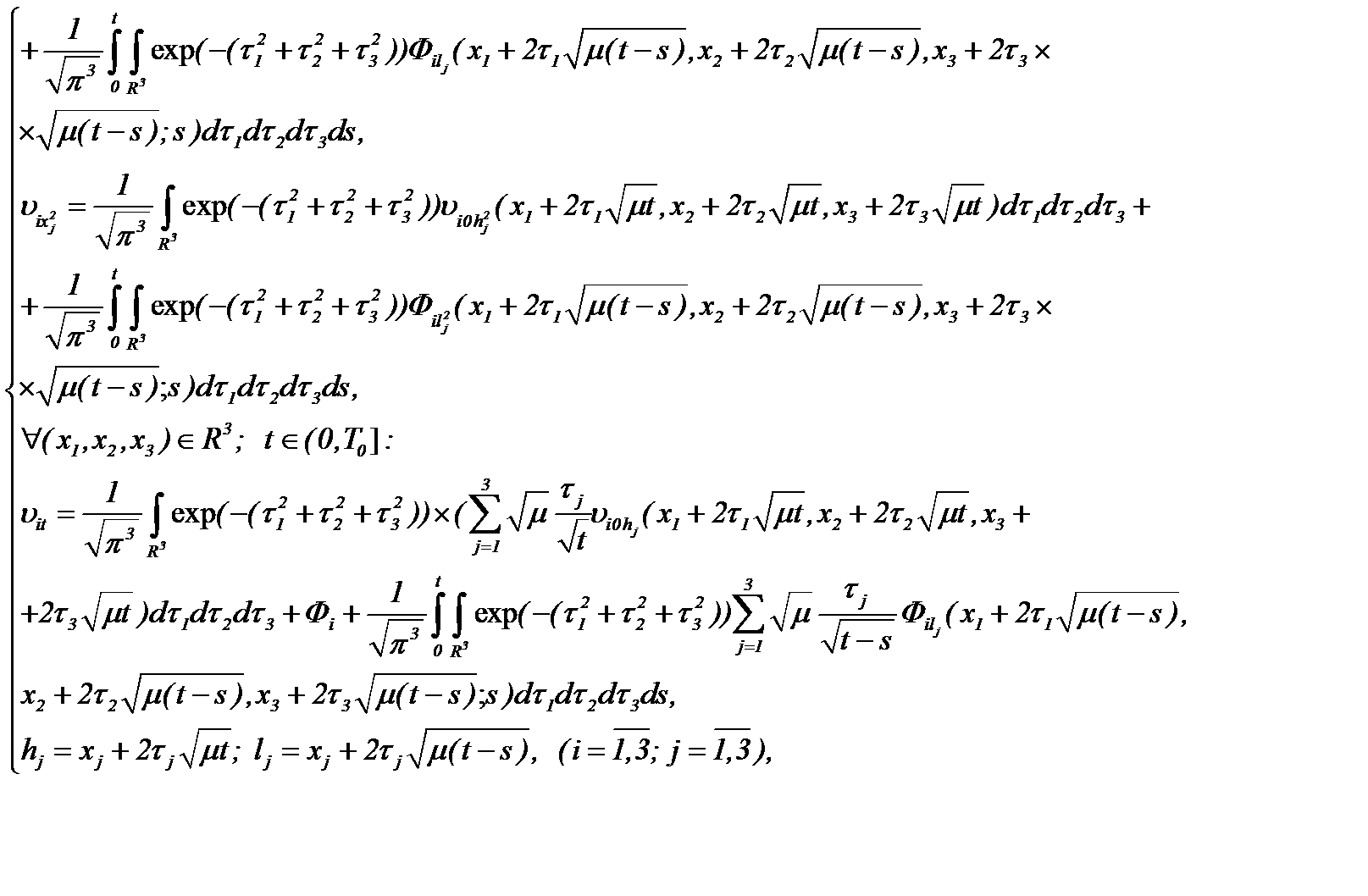 (2.11)
(2.11)
а, затем, подставляя (2.11) в (2.10), имеем
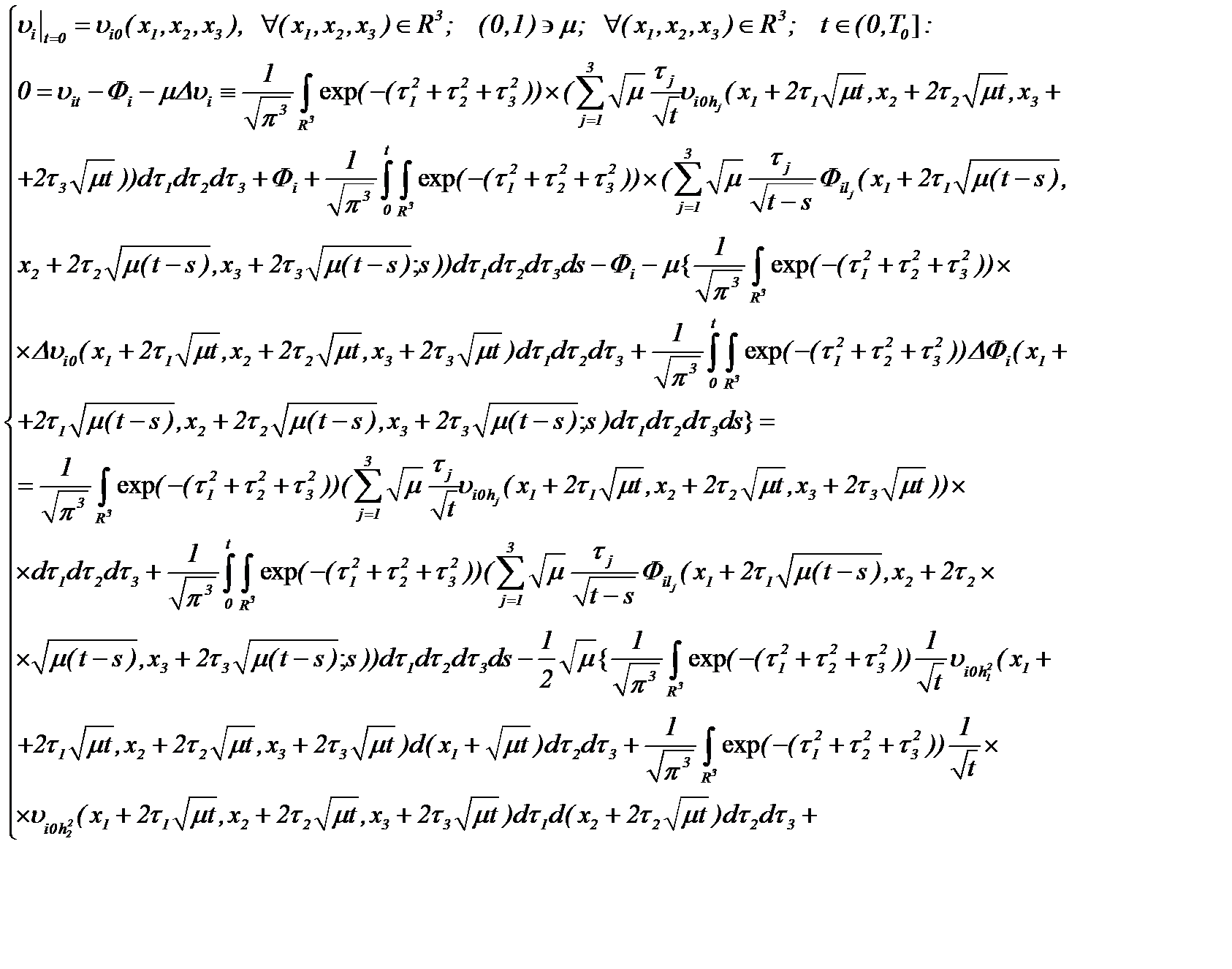
 (*)
(*)
где правая часть формулы (*) интегрирована по частям, что и требовалось доказать.
Далее покажем, что решение (2.10) удовлетворяет (1.2). Для этого, учитывая частные производные первого порядка и суммируя эти производные с учетом (1.2), имеем
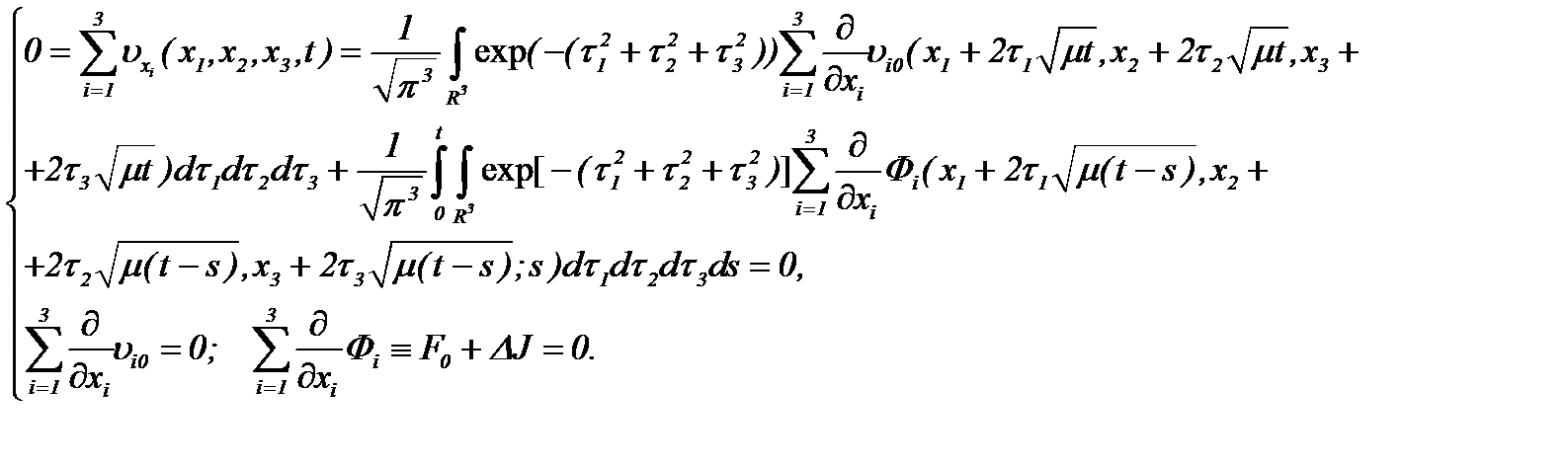
Значит, система (2.10) удовлетворяет уравнению (1.2).
Доказательство ограниченности решений в  предполагает, чтобы решение системы (1.1) было дано в форме (2.10) с условиями (1.2), (1.3), (A1), (2.1) и
предполагает, чтобы решение системы (1.1) было дано в форме (2.10) с условиями (1.2), (1.3), (A1), (2.1) и
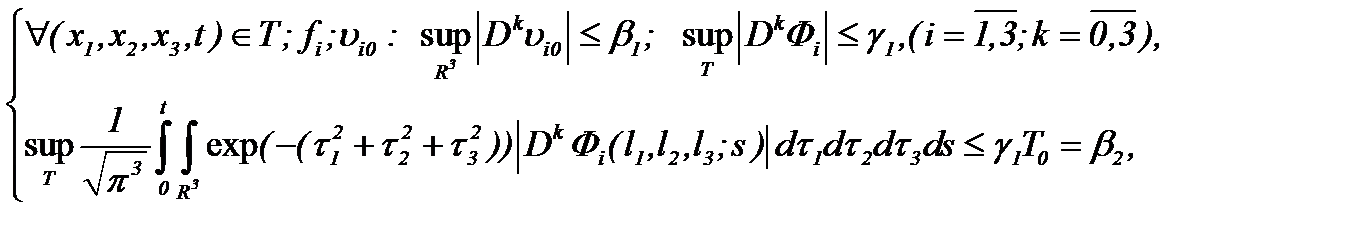
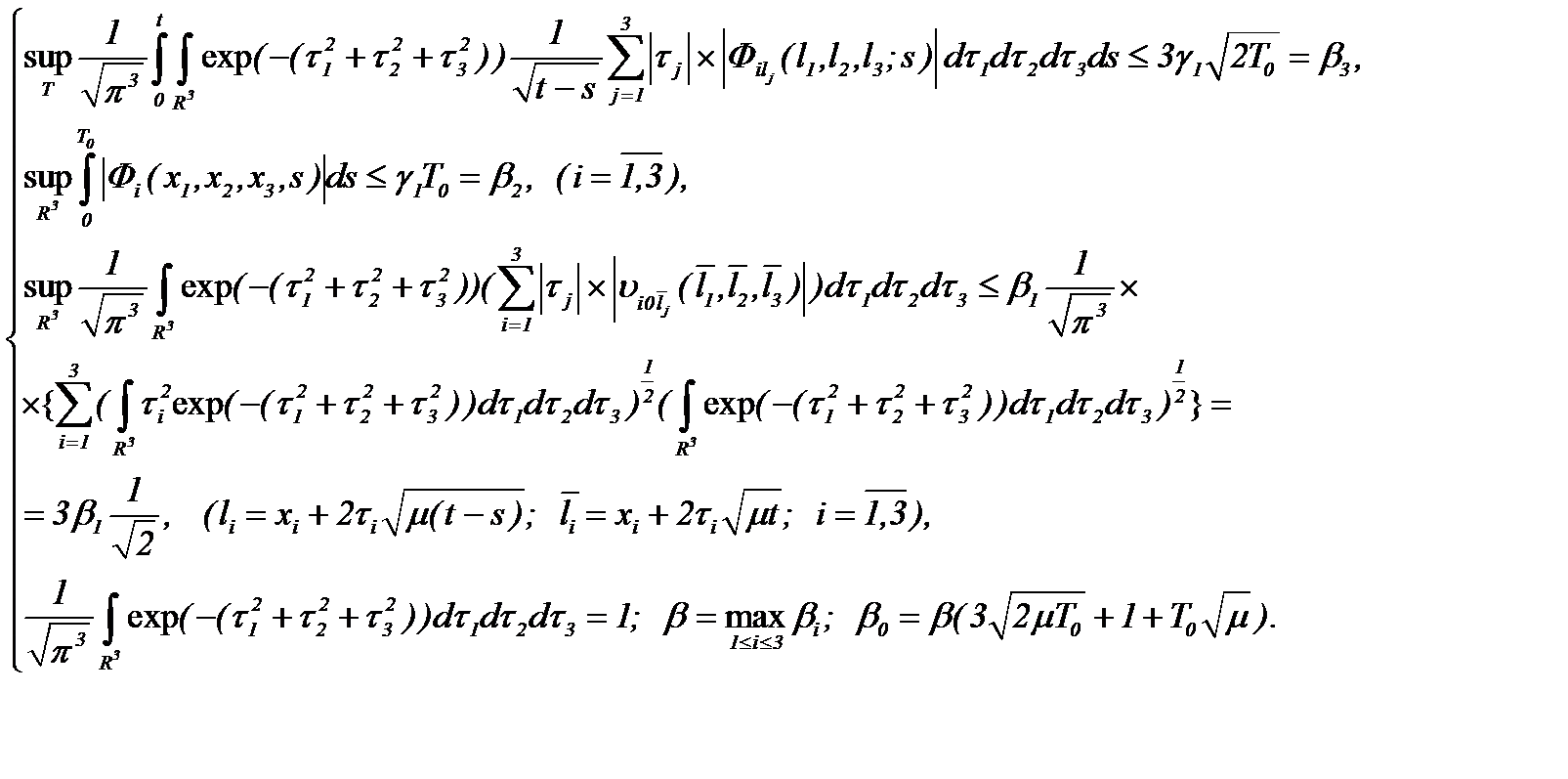 (2.12)
(2.12)
Действительно, оценивая (2.10) в 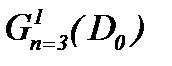 , имеем
, имеем
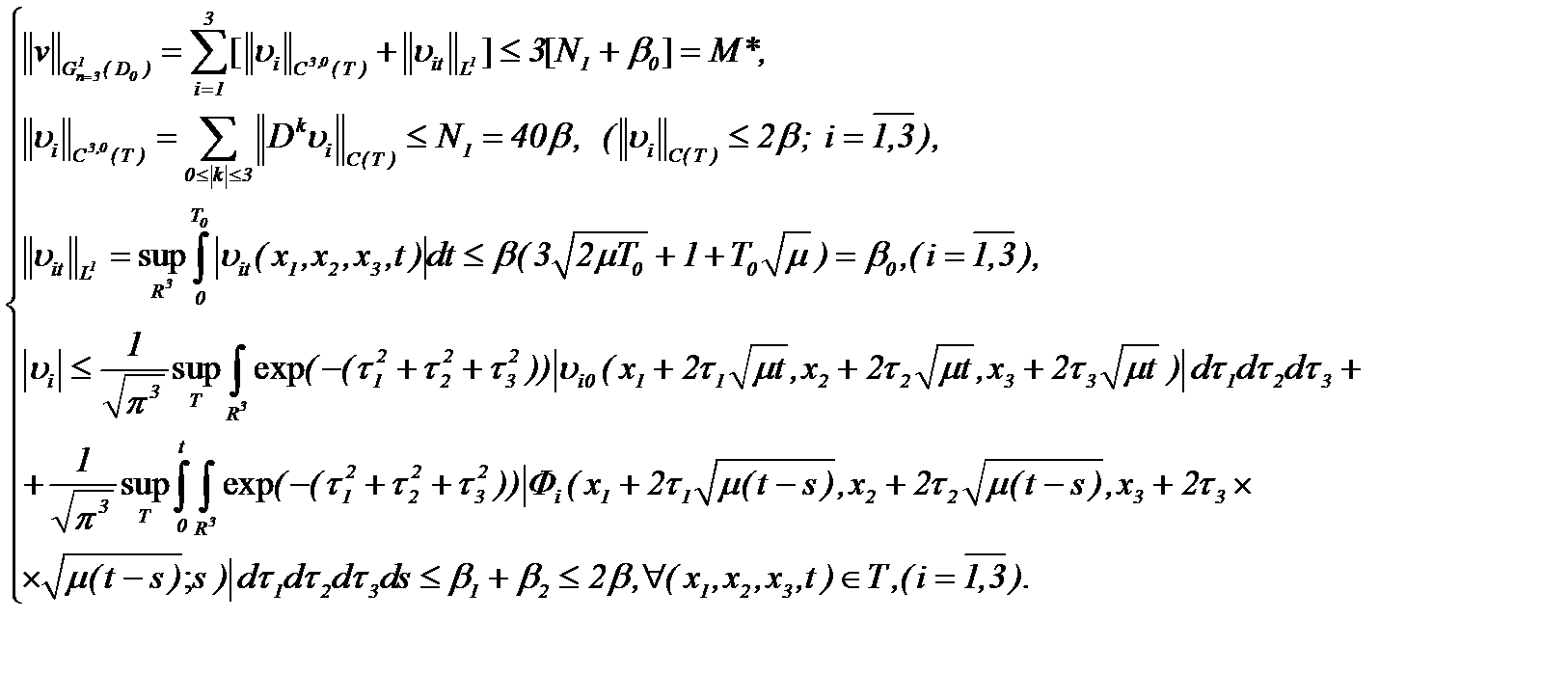
Единственность решения 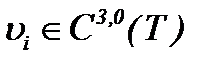 системы (2.10) очевидна из метода от противного [13]. В самом деле, предполагая
системы (2.10) очевидна из метода от противного [13]. В самом деле, предполагая 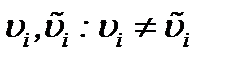 и допуская, что эти решения удовлетворяют системе (2.10), с условием (1.3), получим противоречие
и допуская, что эти решения удовлетворяют системе (2.10), с условием (1.3), получим противоречие 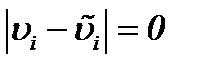 , поэтому система (2.10) имеет единственное решение.
, поэтому система (2.10) имеет единственное решение.
Из результатов (2.10) при условиях (A1), (2.1) следует, что гладкость функций налагается только по 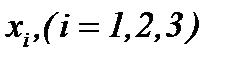 , так как производная первого порядка по времени определяется для
, так как производная первого порядка по времени определяется для 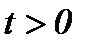 .
.
Замечание 1. Помимо всего, альтернативно можем рассмотреть, например, класс подходящих решений, построенных в 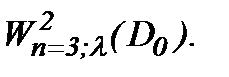
Если решение системы (1.1), представлено в виде (2.10) с условиями (1.2), (1.3), (A1), (2.12) и
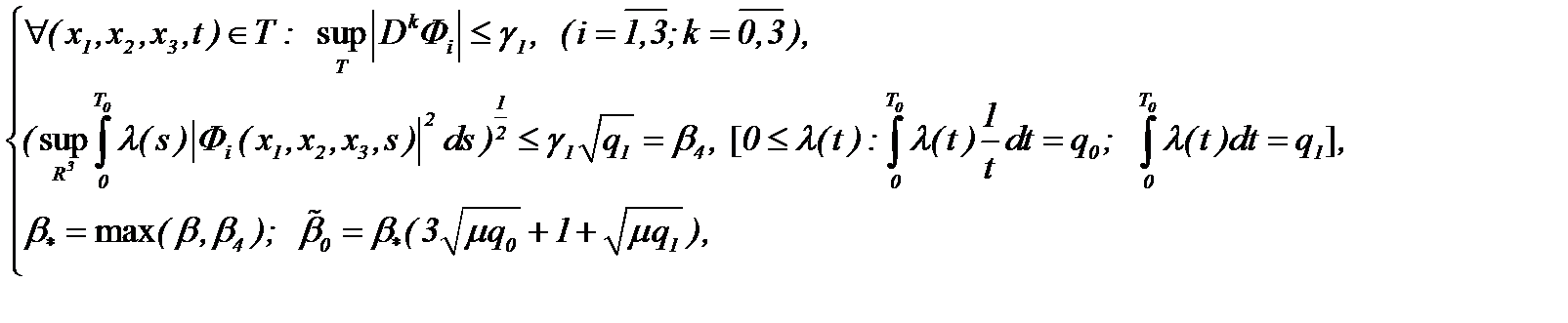 (2.13)
(2.13)
то решение (2.10) задачи Навье-Стокса (1.1) – (1.3) принадлежит 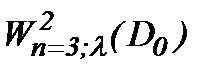 .
.
Действительно, на основе (2.10), проведя оценки в 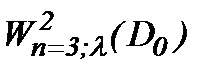 , получим [8]:
, получим [8]:
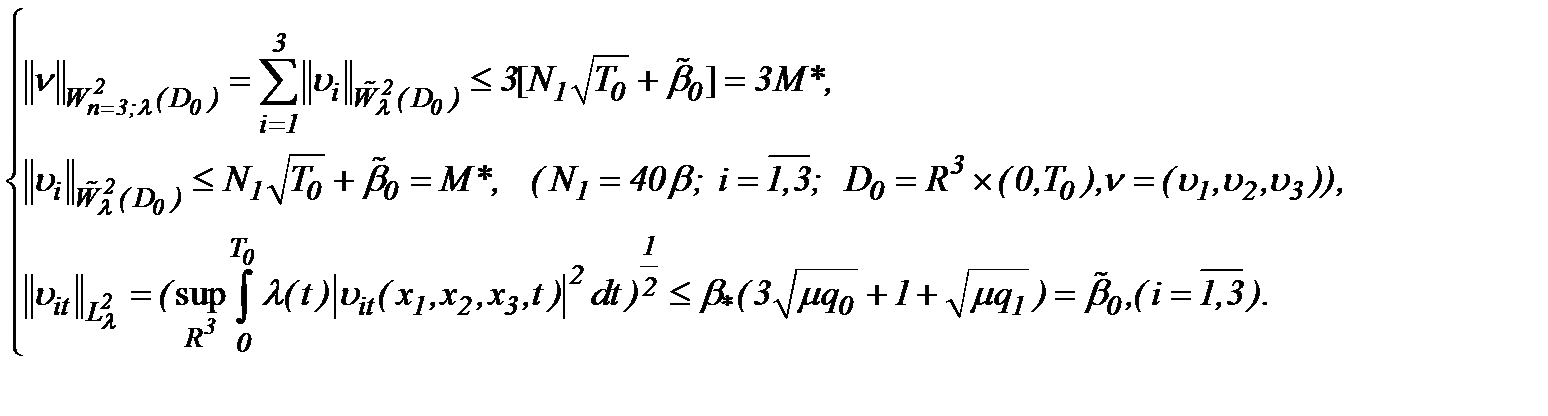
Отметим, что в работе [8] аналогичные результаты в случае (2.10) получены и в весовом пространстве 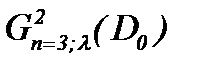 .
.
3) Суть данного подпункта в определении решения (2.9) в 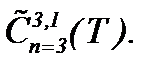 Для этого, задачу (2.9), (1.3) можно решить иначе, если выполняются условия:
Для этого, задачу (2.9), (1.3) можно решить иначе, если выполняются условия:
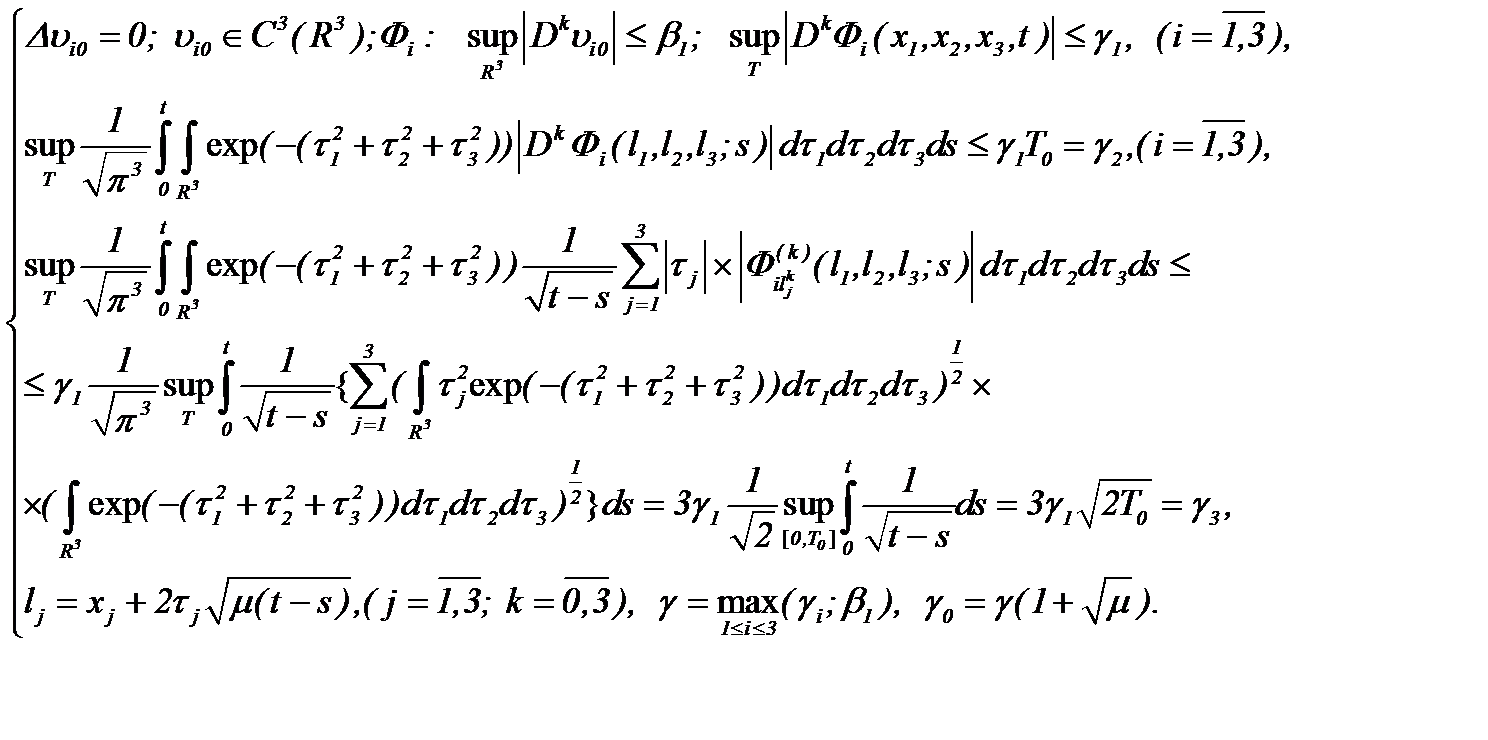 (2.12)*
(2.12)*
Тогда компоненты скорости  определяются по правилу
определяются по правилу
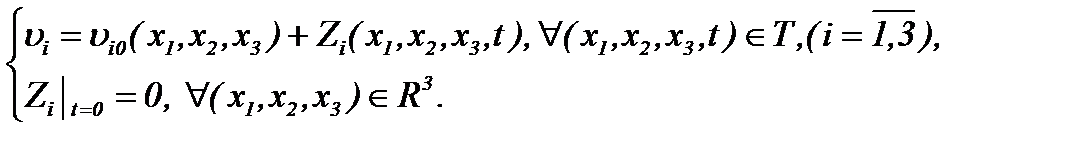 (2.14)
(2.14)
Поэтому система (2.9) преобразуется к виду
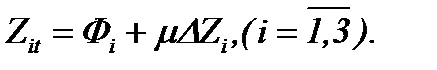 (2.15)
(2.15)
Здесь 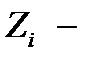 новые неизвестные функции, которые определяют решение задачи Навье-Стокса
новые неизвестные функции, которые определяют решение задачи Навье-Стокса
на основе (2.14) в следующем виде
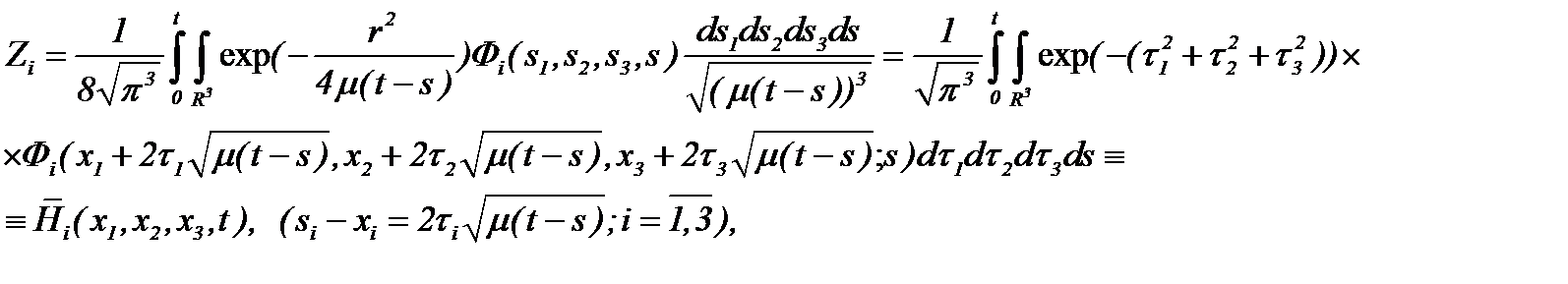 (2.16)
(2.16)
где 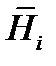 – известные функции, а потому найденное решение (2.16) удовлетворяет систему (2.15).
– известные функции, а потому найденное решение (2.16) удовлетворяет систему (2.15).
Вычислив частные производные системы (2.16)
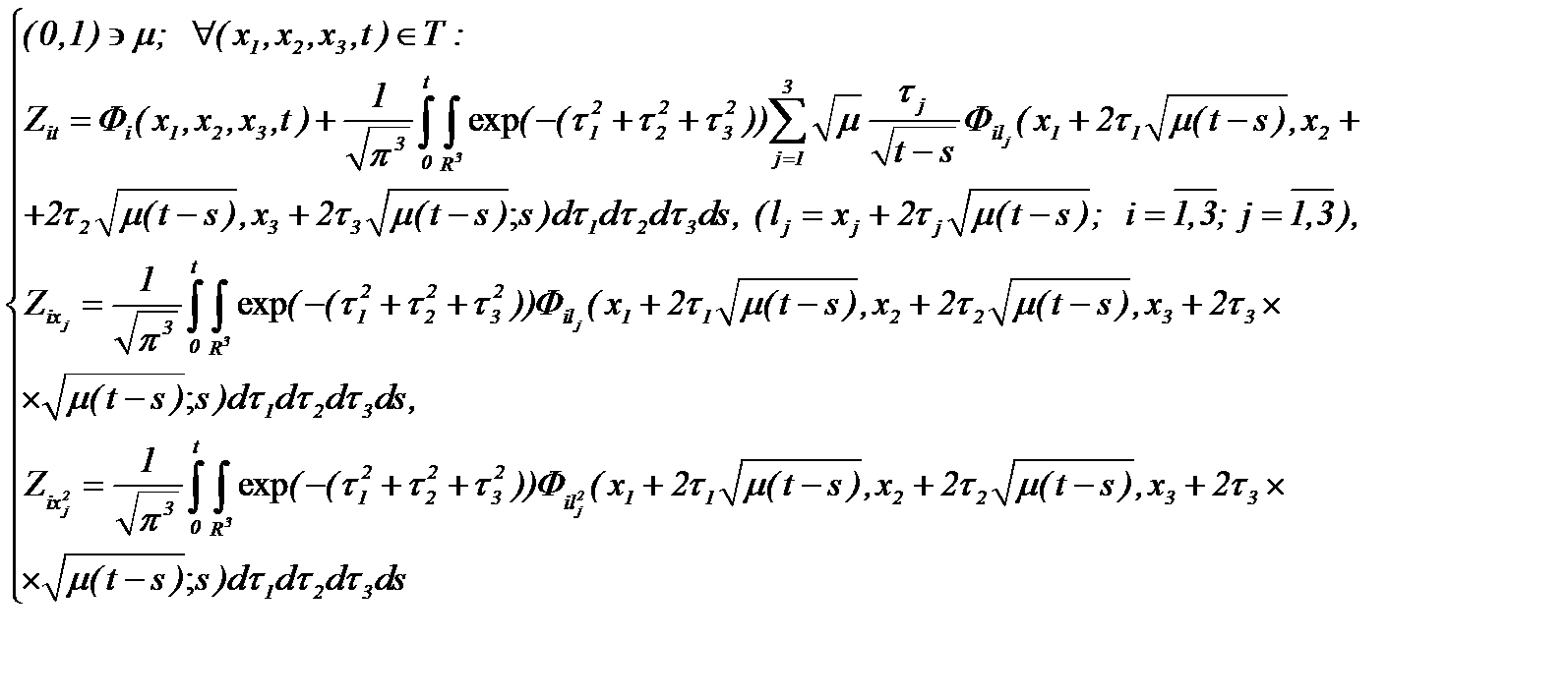 (2.17)
(2.17)
и подставляя (2.17) в (2.15), имеем (см. (*)):
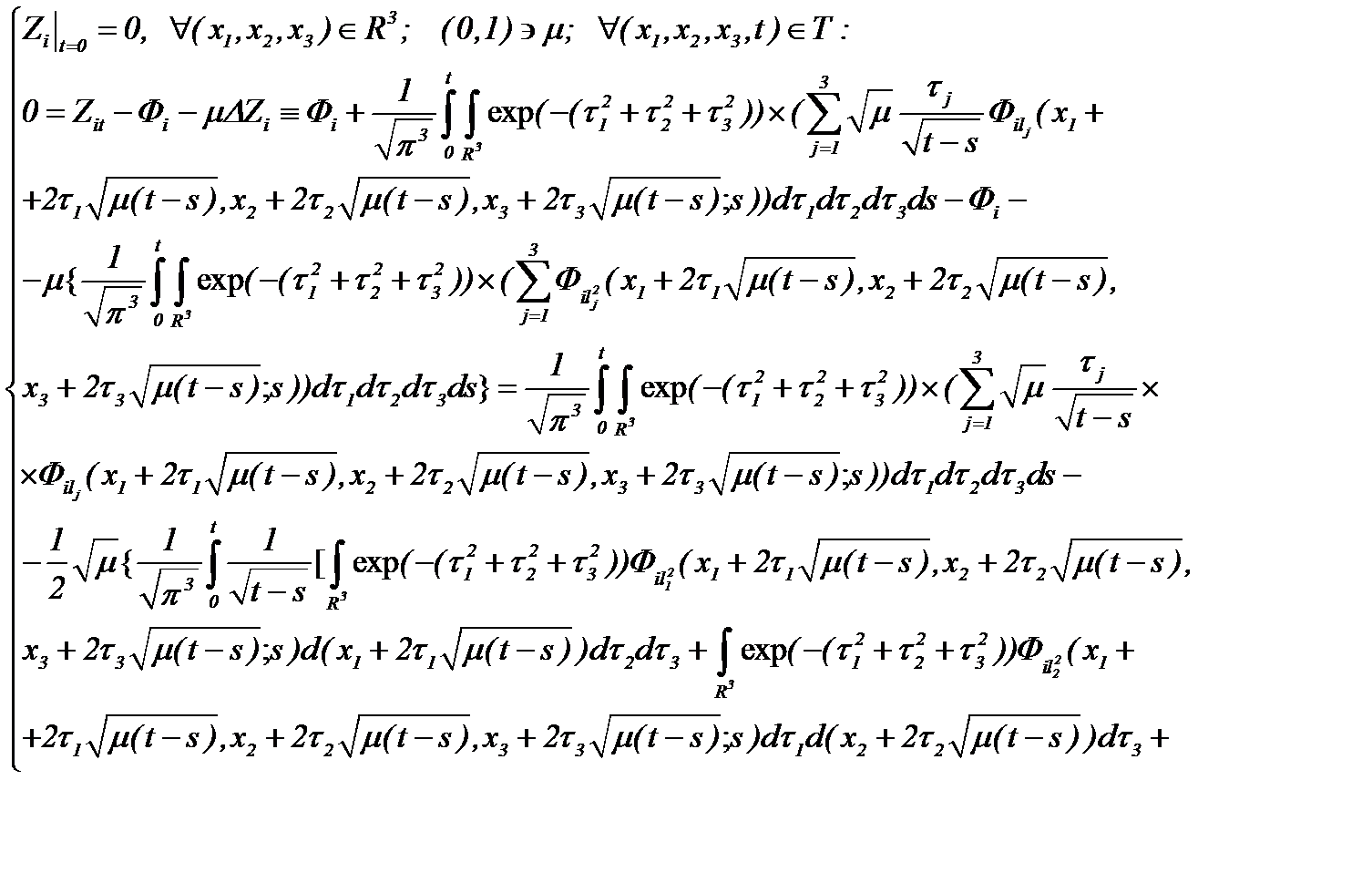
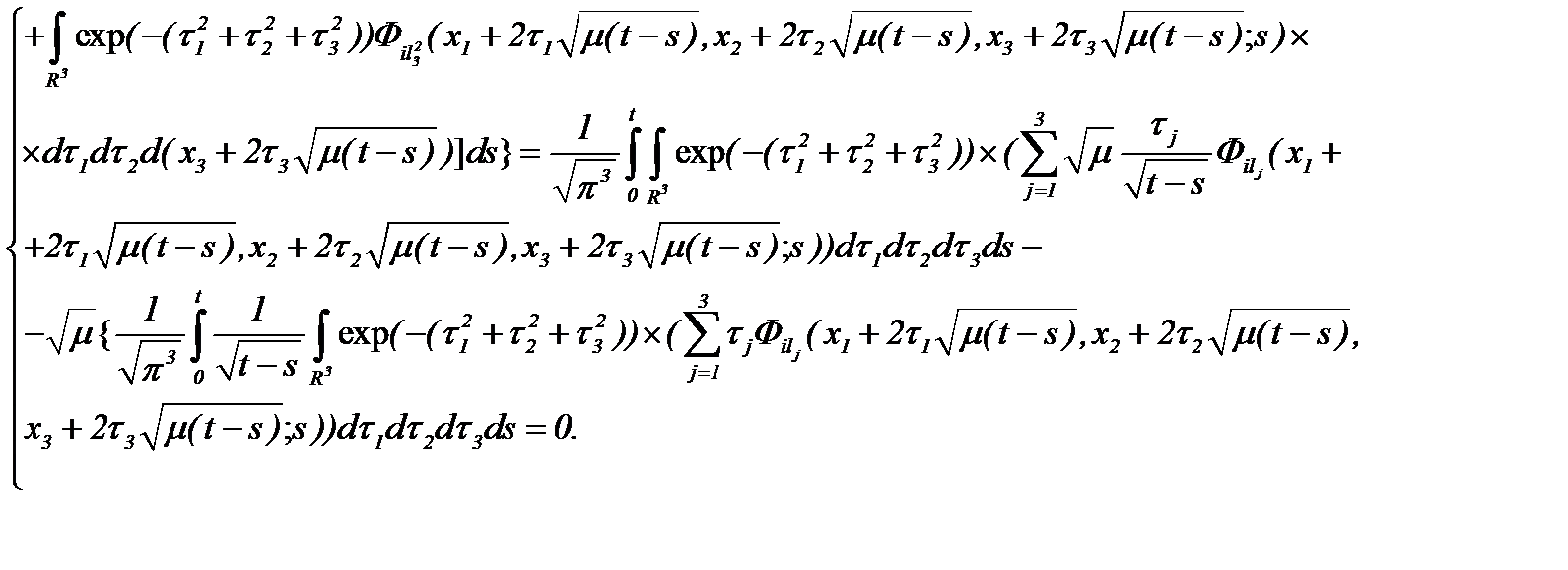 (2.18)
(2.18)
А это именно то, что и требовалось доказать.
Значит, на основании (2.14) и (2.16) получим
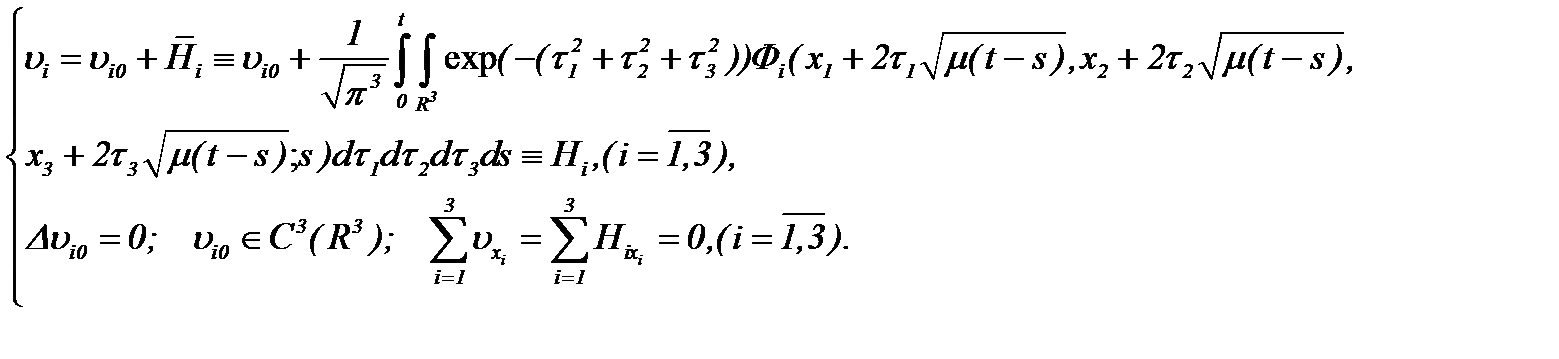 (2.19)
(2.19)
Доказательство ограниченности функций 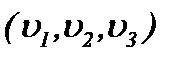 в
в 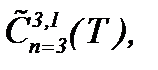 когда решение системы (1.1) представляется в форме (2.19) с условиями (1.2), (1.3), (A1), (2.1) и (2.12)*, проводится на основе результатов теоремы 1. Поскольку функции
когда решение системы (1.1) представляется в форме (2.19) с условиями (1.2), (1.3), (A1), (2.1) и (2.12)*, проводится на основе результатов теоремы 1. Поскольку функции 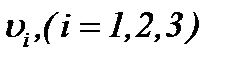 являются решениями системы (2.19), то, вычисляя частные производные до требуемого порядка и оценивая в смысле нормы
являются решениями системы (2.19), то, вычисляя частные производные до требуемого порядка и оценивая в смысле нормы 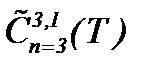 , имеем
, имеем
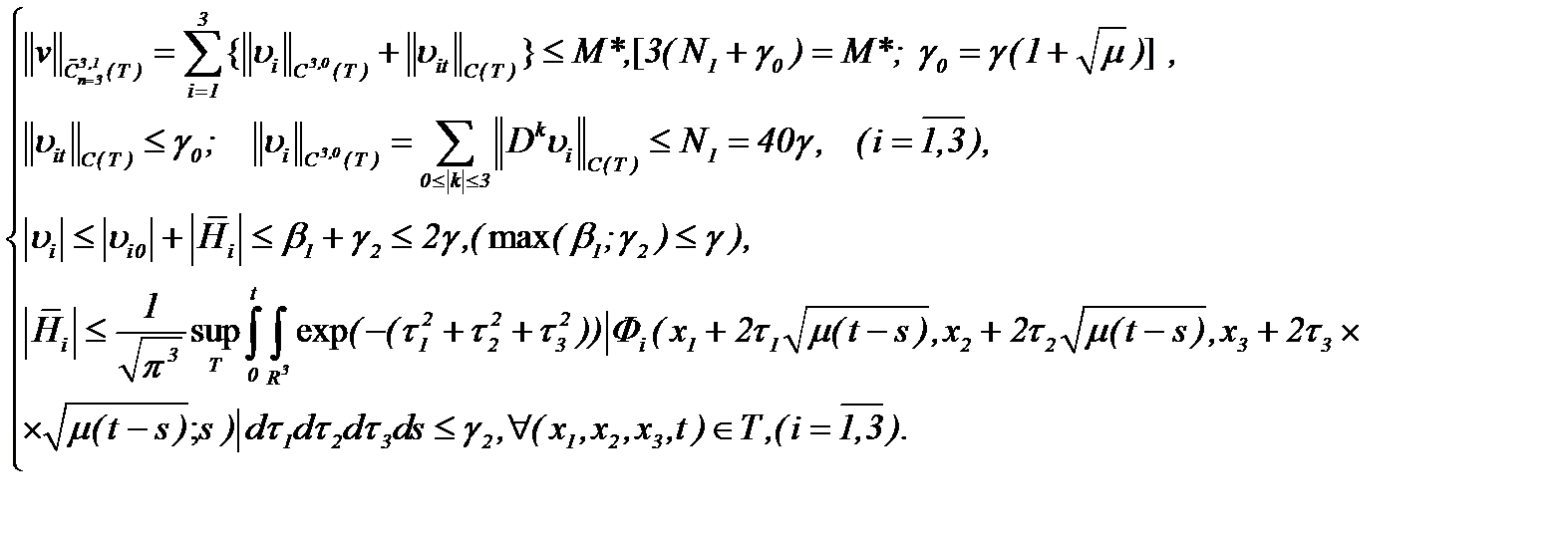 (2.20)
(2.20)
Единственность очевидна, так как на основе метода от противного из (2.16) следует единственность решения данной системы. Тогда, с учетом (2.19) получим единственность решения системы (2.2) в 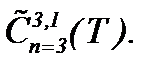
4) Возвращаясь к доказательству теоремы 1, теперь, с учетом (2.3), (2.19) и их частных производных по 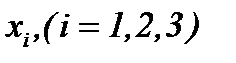 , находим
, находим
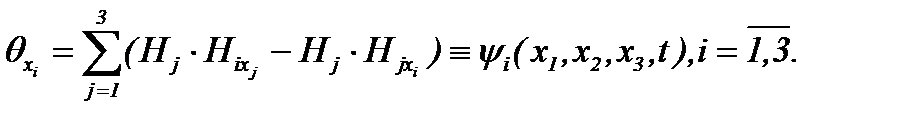 (2.21)
(2.21)








