VI . Магнитные цепи.

Дата: 2025-05-01; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

1. Магнитные цепи при постоянных магнитных потоках.

Магнитная цепь- совокупность феррамагнитных тел и воздушных сред,по которым замыкается магнитный поток.

Магнитные цепи являются частью электротехнического устройства и предназначены для создания в заданном объеме магнитного поля нужной интенсивности.

В неразветвленных магнитных цепях поток сечений каждого участка один и тот же.

2. Закон Ома и законы Кирхгофа для магнитных цепей.

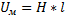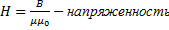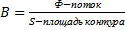, , – индукция

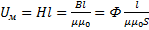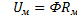, -закон Ома для магнитной цепи, 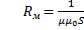- магнитное сопротивление , 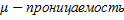, 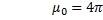* 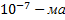гнитная постоянная

Ф= 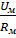, В замкнутом контуре : Ф=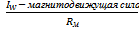

1 закон Кирхгофа вытекает из принципа непрерывности линий магнитной индукции: В любом узле сложной магнитной цепи алгебраическая сумма магнитных потоков равна 0.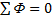

Магнитные потоки направленные к узлу берут со знаком “+”, а выходящие из узла со знаком “-”.

Сумма приходящих к узлу магнитных потоков равна сумме выходящих из узла магнитных потоков.

2 закон Кирхгофа :В любом разомкнутом контуре сложной магнитной цепи алгебраическая сумма магнитных U равна сумме 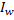действующих в этом контуре.

,

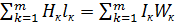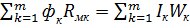
Достоинство этих законов в том, что они помогают провести аналогию между электрическими и магнитными цепями,которая позволяет применять для расчета магнитных цепей те же методы,что и для расчета н.э.ц.

Электрическая цепь Магнитная цепь
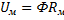1. Действует ЭДС, Е. 2. ЭДС вызывает ток. 3. U=IR, R имеет ВАХ. 4. 1 закон Кирхгофа ∑I=0. 5. 2 закон Кирхгофа ∑U=0. 1. Действует МДС, F=Iw 2. МДС вызывает поток 3. 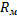имеет вебер-амперную хар-ку 4. 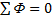5.

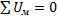
Вывод: возможно использование схем замещения для магнитных цепей постоянного магнитного потока в виде графического изображения элементов магнитной цепи подобных элементам электрической цепи.

3.Расчет неразветвленных магнитных цепей.

При расчете необходимо знать 3 основных соотношения, при использовании которых считаем,что магнитное поле однородное ; B, H, dl- совпадают по направлению.

Ф=BS, ,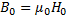

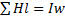
Кроме того необходимо знать кривую намагничивания ферромагнитного сердечника. B=B(H)

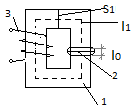
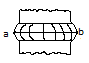цепь состоит из магнитопровода 1 с воздушным зазором 2 и намагничивающей обмотки 3. Считается,что в такой цепи магнитный поток одинаков во всех сечениях,т.е. пренебрегает потоками рассеив-я .

Сечение воздушного зазора 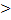сечения магнитопровода. Из-за явления выпучивания магнитно-силовых линий.

Площадь зазора определяется поперечным размером a,b.

В большинстве практических задач явлением выпучивания пренебрегают. И считают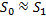


Прямой задачей задается значение магнитного потока или индукция в зазоре, геометрические размеры сечения магнит.-провода, 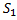, , 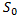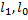и характеристика намагничивания магнитопровода. Требуется найти магнитодвижущую силу . Порядок решения:

1. по 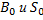находим поток Ф=

2.

 

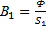
3. по кривой намагнич-я материала сердечника для полученного значения В1 находят направ-сть магнитного поля Н1 в сердечнике.

4. 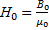= 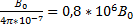5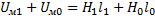. Iw= 6. Iw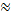

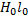
Обратная задача: заключается в том,что задают Iw=F. Нужно определить индукцию в зазоре В0.

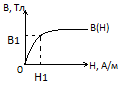
Решение: задаются несколькими произвольными значениями магн. индукции в зазоре и определяют для них магнитодвижущую силу. По полученным значениям строят зависимость Iwk=f(B0k) и получают график зависимости:

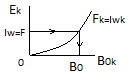По зависимости определяют какая В0 соответствует заданной величине МДС.

Iw=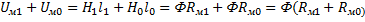

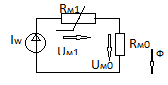Магнитное сопротивление всей цепи равно сумме магнитных сопротивлений ее последовательно соединенных участков. Схема замещения магнитной цепи:

По закону Ома: Ф=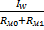

Поскольку магнитное сопротивление является величиной не линейной и зависимой от величины магнитной индукции,то решение находятся методом последовательных приближений. Этот процесс заканчивают при достижении заданной точности расчета.

Графо-аналитический метод:

,

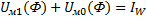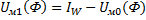
Полученное не линейное уравнение решается графически,путем построения 2х вебер-амперных хар-к.

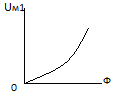
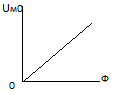
Для построения этих функций рассчитывается ряд значений в соответствии с табл. для параметров исходной магнитной цепи.

В1 Ф=ВS H Uм1=H1l1 B0=Ф/S0 H0 Uм0=H0l0 Iw-H0l0
Тл Вб А/м А Тл А/м А А

 

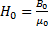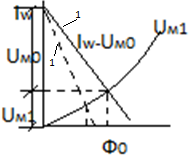, Точка пересечения определяет значение потока в сердечнике 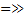поток будет одинаковый и в сердечнике и в зазоре . 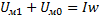, 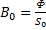.При увеличении воздушного зазора хар-ка 1 идет круче и новая т. Пересечения даст уменьшение магнитного потока. Если же поток необходимо оставить прежним,то нужно увеличить значение МДС.

4. Расчет разветвленных магнитных цепей.

 

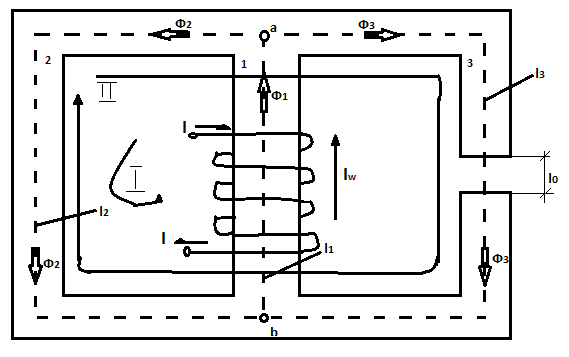
Равлетвленная магнитная цепи с тремя стержнями и одним источником МДС в каждом стержне магнитной цепи протекает свой магнитный поток, составим уравнение по законам Кирхгофа:

Для узла а , Ф1= Ф2+Ф3

Для 1-ого узла , UM2+UM1= IW

Для 2-ого узла , UM1-UM2+ UM0=0.

По закону Ома для магнитных цепей UM=RMФ

Ф1= Ф2+Ф3 RM1Ф1+ RM2Ф2= IW

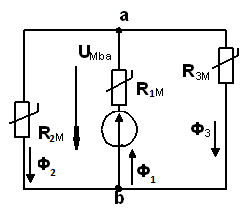RM3Ф3- RM2Ф2+ RM0Ф0=0

Составим расчетную схему замещения:

Схема замещения содержит нелинейные элементы: RM1, RM2, RM3. Удобнее использовать не величинами RM, а Вебер-амперными характеристиками нелинейных элементов Ф(UM). UM=H*l. тогда система уравнений примет вид:

Ф1= Ф2+Ф3 H1l1+ H2l2= IW H3l3- H2l2+ H0l0=0

Прямая задача. Пусть задано значение индукции в зазоре В, или поток в зазоре Ф. определим значение потока: Ф3= В0S0 , S0≈ S3

Определим индукцию В0= Ф3/S3

По значениям В0 и В3 определяем напряженности H0 и H3, затем находим падения магнитного напряжения на развлетвлении (a,b)

UMab= H2l2= H3l3+ H0l0

Находим напряженность во 2-ом стержне H2= UMab/ l2. По напряженности, используя кривую намагниченности определяем В2 и поток Ф2= В2S2. По известным потокам Ф2 и Ф3, определяем поток в первом стержне Ф1= Ф2+Ф3. Зная поток Ф1 определяем индукцию В1= Ф1/S1, по индукции определяем H2. Затем подсчитываем необходимую МДС. H1l1+ H2l2= IW

Обратная задача. Решение проведем графо-аналитически, с использованием метода двух узлов.

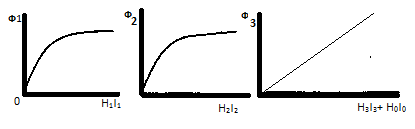Пусть известны характеристики Ф1= Ф1(H1l1); Ф2= Ф2(H2l2); Ф3= Ф3(H3l3+ H0l0).

 

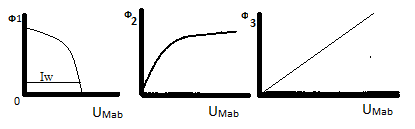Если заданы геометрические размеры магнитоповода (l1, l2 l3 l0 S0 S1 S2 S3 ) и кривая намагниченности сталемагнитного провода В=В(Н), то указанные характеристики можно посторить задаваясь различными значениями магнитной индукции В, и находя по ним значения напряженности Н.

Затем определяют поток Ф= ВS и магнитное напряжение UM=H*l.

Обычно составляют расчетную таблицу:

В3 Ф3= В3S3 Н3 H0=B0/µ0 H3l3+ H0l0
л Вб А/м А/м A

 

Складывать потоки Ф2 и Ф3 непосредственно нельзя, т.к. имеют разные аргументы. Необходимо построить потоки Ф1, Ф2,Ф3 в функции одного общего аргумента. Общим аргументом для всех 3-х ветвей является магнитное напряжение между двумя узлами (а и b)

Для 2-го стержня UMab= H3l3+ H0l0, для 1-го стержня UMab= H2l2= IW + H1l1.

Если выразить потоки Ф1, Ф2,Ф3 через узловое напряжение, то получим характеристики:

 

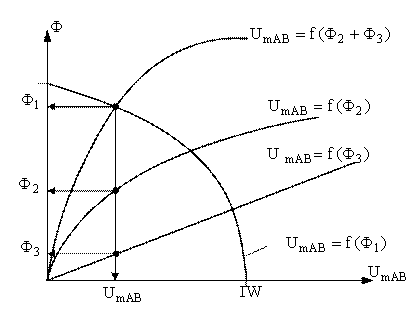
Поскольку все функции имеют одинаковый аргумент, построим их на одном графике:

 

Точка пересечения кривой Ф2 + Ф3 с кривой Ф1, дает рабочую точку. По ней определяем потоки во всех стержнях и узловое магнитное напряжение.

5. Магнитные цепи переменного тока.

Если намагниченную обмотку,расположенную на ферромагнитном сердечнике подключить к источнику переменного U, то по обмотке будет протекать переменный ток, который будет создавать переменный магнитный поток.

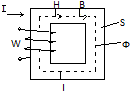u = 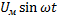е= - W 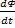u= -e= W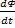

Закон изменения переменного магнитного потока:

Ф= = = = ,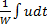

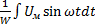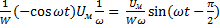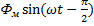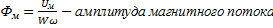
Уравнение показывает,что если U изменяется по синусоидальному закону,то и поток также изменяется по син-му закону, но отстает от U по фазе на 90 .

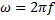, амплитуда питающего 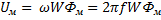, действующее значение U=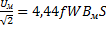

определим форму тока в катушке:

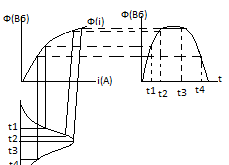Она подобна зависимости В= В(Н), т.к. Ф=ВS, а Н= Iw. По этой зависимости и син-ой форме магнитного потока построим форму намагниченного потока.

Намагниченный ток имеет не синусоид-ую форму, он содержит основную гармонику и высшие гармоники. Причина нессин-сти тока не линейная зависимость В=В(Н). часто на практике не синусоид-ую кривую заменяют эквивалентной синусоидой , это дает возможность изобразить ток в виде вектора на векторной диаграмме.

Петля Гистерезиса :

 

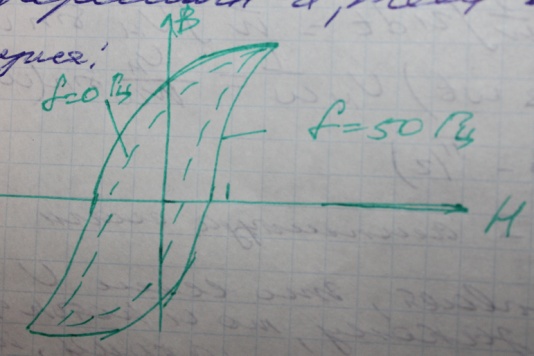
Если учесть потери в стали ,активное и реактивное сопротивление обмотки,то можем построить схему замещения:

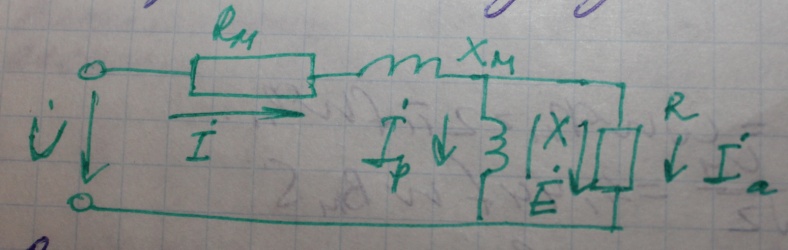
Для этой схемы составляем систему комплексных уравнений

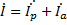
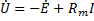: +j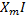

 

VII . Теория электромагнитного поля.

1. Электромагнитное поле и его уравнение в интегральной форме.

Электромагнитное поле является особым видом материи. Оно может существовать в свободном ,отделенным от заряженных частиц состоянии в виде движущихся со скоростью близкой к световой (С=299792458 м/с) фотонов или вообще в виде излученного движущейся с этой скоростью элетромагнитного поля (волн). Электромагнитное поле является носителем количества энергии (определенного), обладает также и определенной соответственной этой энергии массой:

m=E/C2.

Однако плотность массы в использованных обычно электромагнитных полях весьма мала. Ничтожная плотность массы, используемых на практики электромагнитных полей дает основание обычно не интересоваться этой характеристикой поля и обращать внимание в основном на энергетическую сторону рассматриваемых явлений.

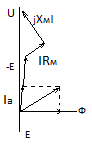
Связь между электрическим тоном и напряженностью магнитного поля устанавливается запасом полного тока. 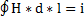- линейный интеграл напряженности магнитного поля по любому методу замкнутому контуру равен полному сквозь поверхность ограниченную этим контуром.

2. ЗАКОН ПОЛНОГО ТОКА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ (ПЕРВОЕ УРАВНЕНИЕ МАКСВЕЛЛА )

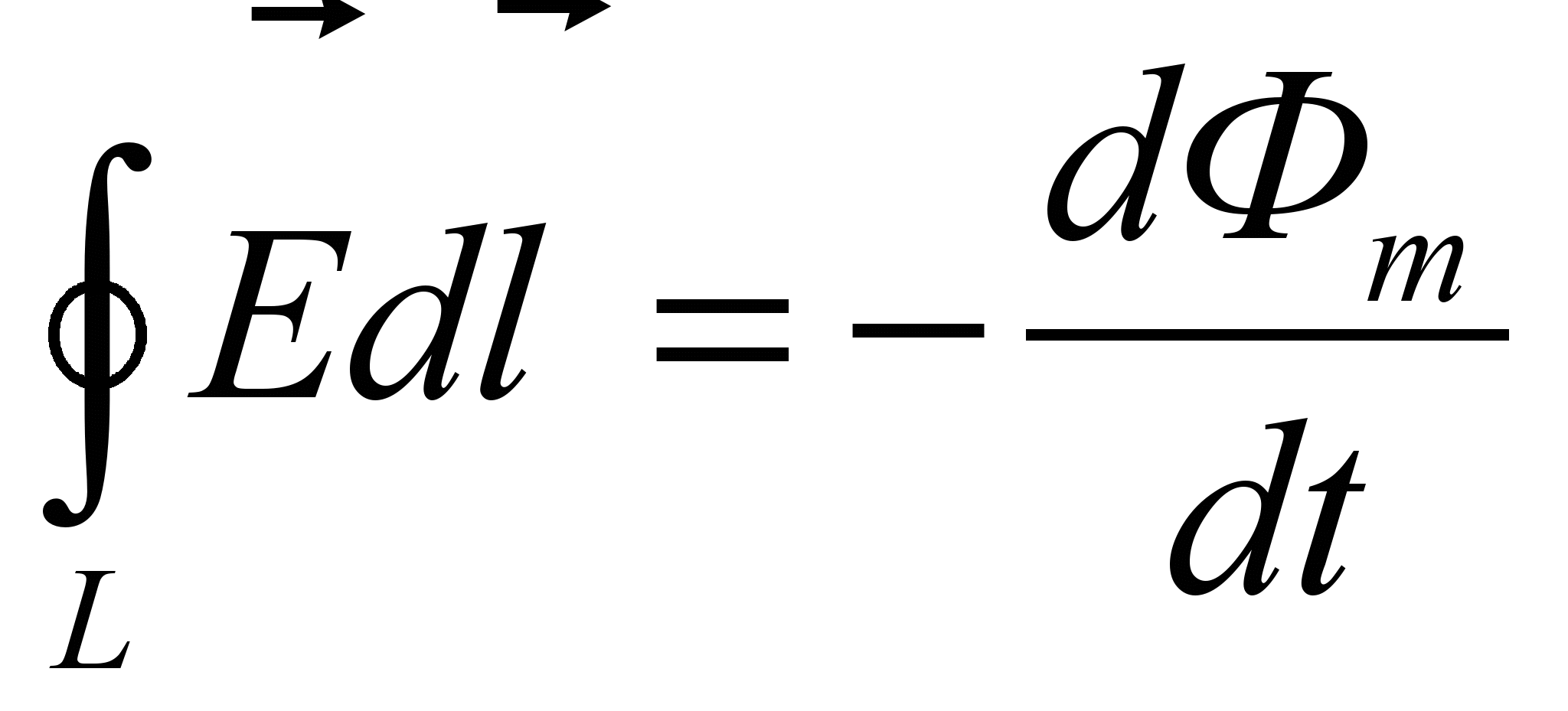  1. Первое уравнение Максвелла является обобщением закона электромагнитной индукции, которое в интегральной форме имеет вид

    1. Из выражения для магнитного потока следует
      →

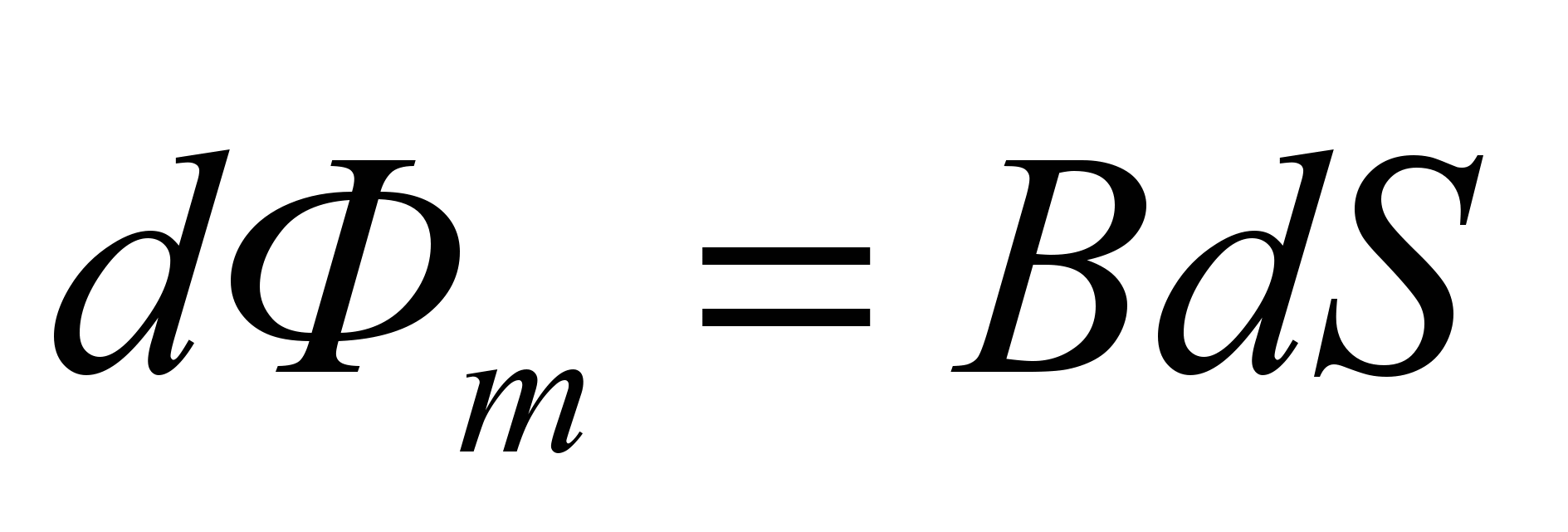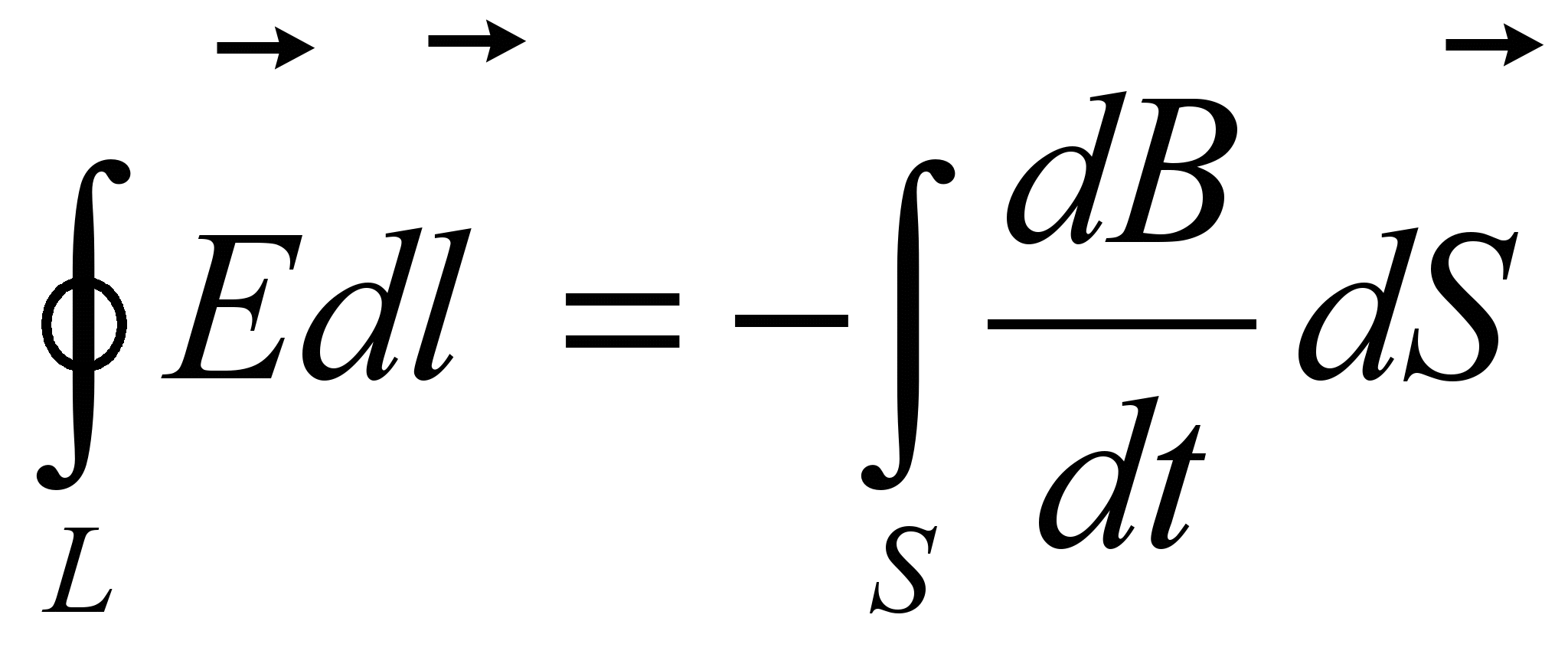
      Интеграл в правой части является функцией только от времени.

    1. Неравенство нулю циркуляции вектора напряженности электрического поля по замкнутому контуру означает, что возбуждаемое переменным магнитным полем электрическое поле является вихревым, как и само магнитное поле.
    2. Из первого уравнения Максвелла следует, что всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле.
    3. По теореме Стокса в векторном анализе


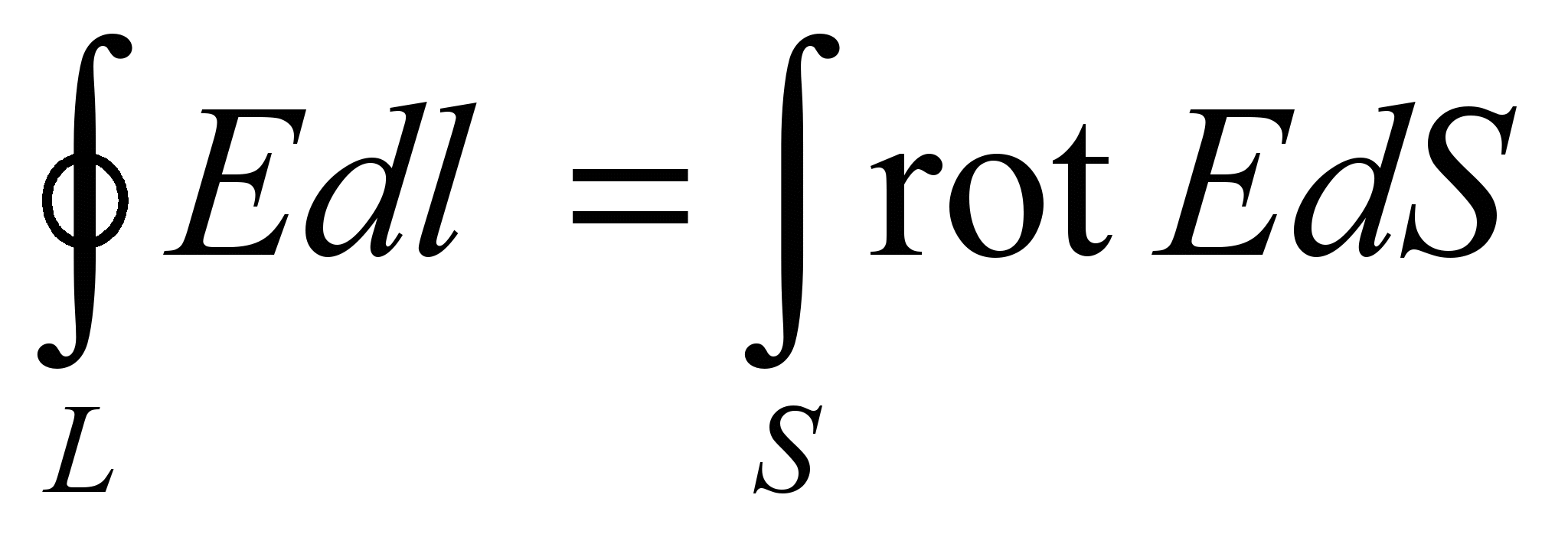,где ротор вектора Е выражается определителем

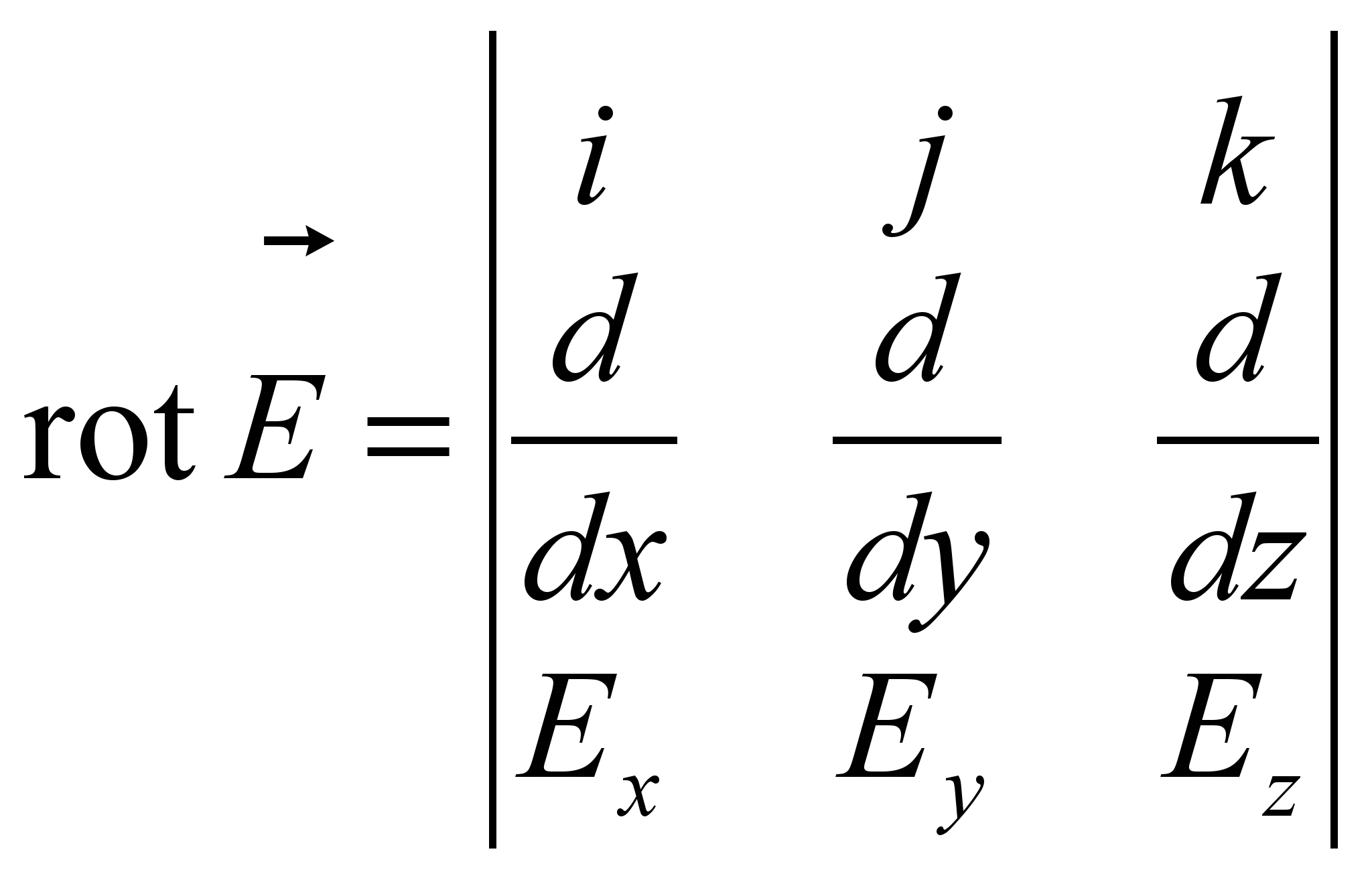что позволяет записать первое уравнение Максвелла в дифференциальном виде

 

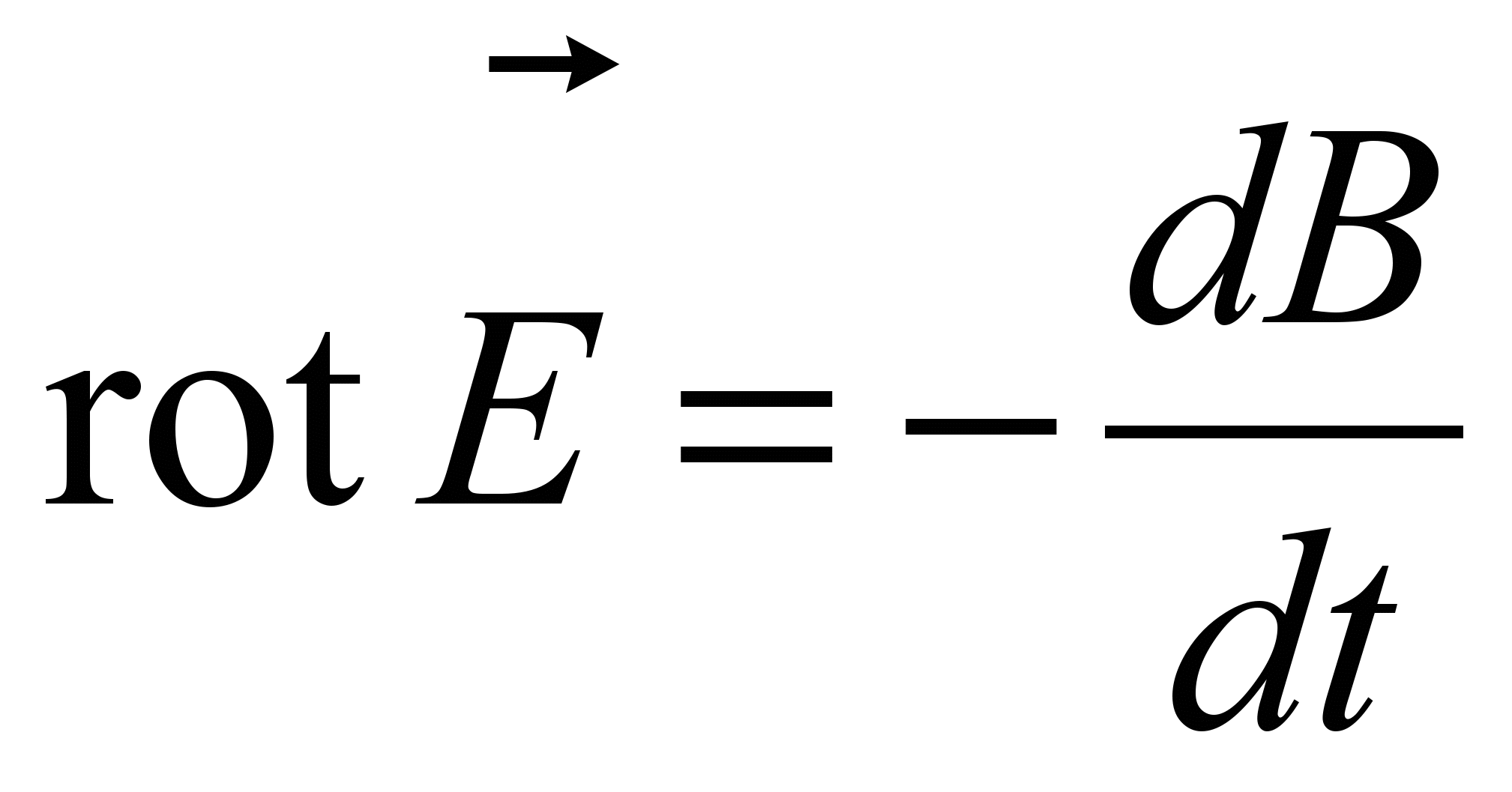
3. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ(ВТОРОЕ УРАВНЕНИЕ МАКСВЕЛЛА)

Второе уравнение Максвелла представляет собой обобщение закона полного тока.

    1. Второе уравнение Максвелла основано на предположении, что всякое изменение электрического поля вызывает возникновение в окружающем пространстве вихревого магнитного поля.
    2. Количественной мерой магнитного действия переменного электрического поля является ток смещения.
    3. Током смещения сквозь произвольную замкнутую поверхность S называется физическая величина, равная потоку вектора плотности тока смещения сквозь эту поверхность


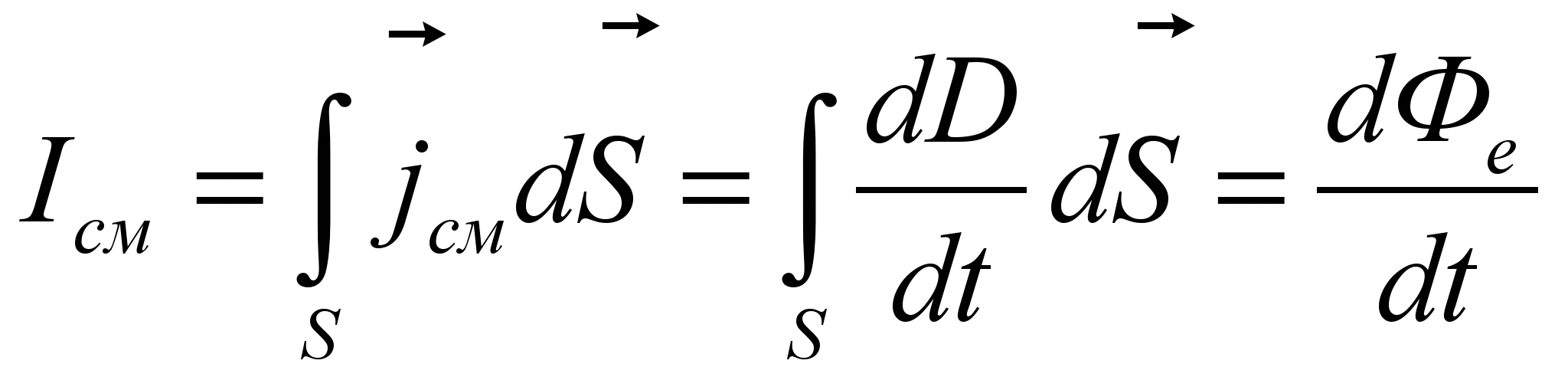с плотностью тока смещения 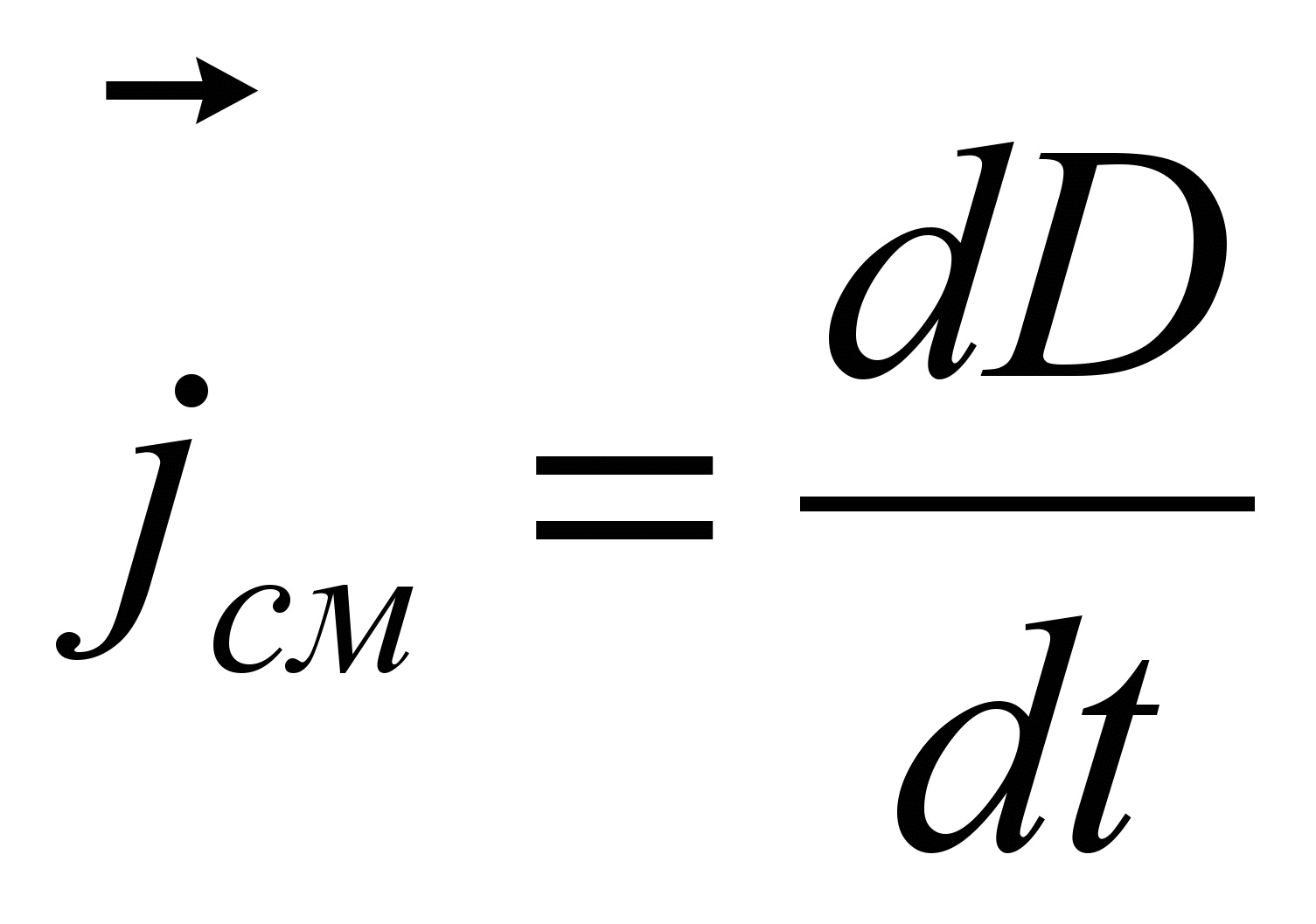, где D –вектор электрического смещения.

 

    1. Токи смещения проходят по тем участкам цепи переменного тока, где отсутствуют проводники (например, между обкладок конденсатора).
    2. В диэлектрике вектор электрического смещения равен
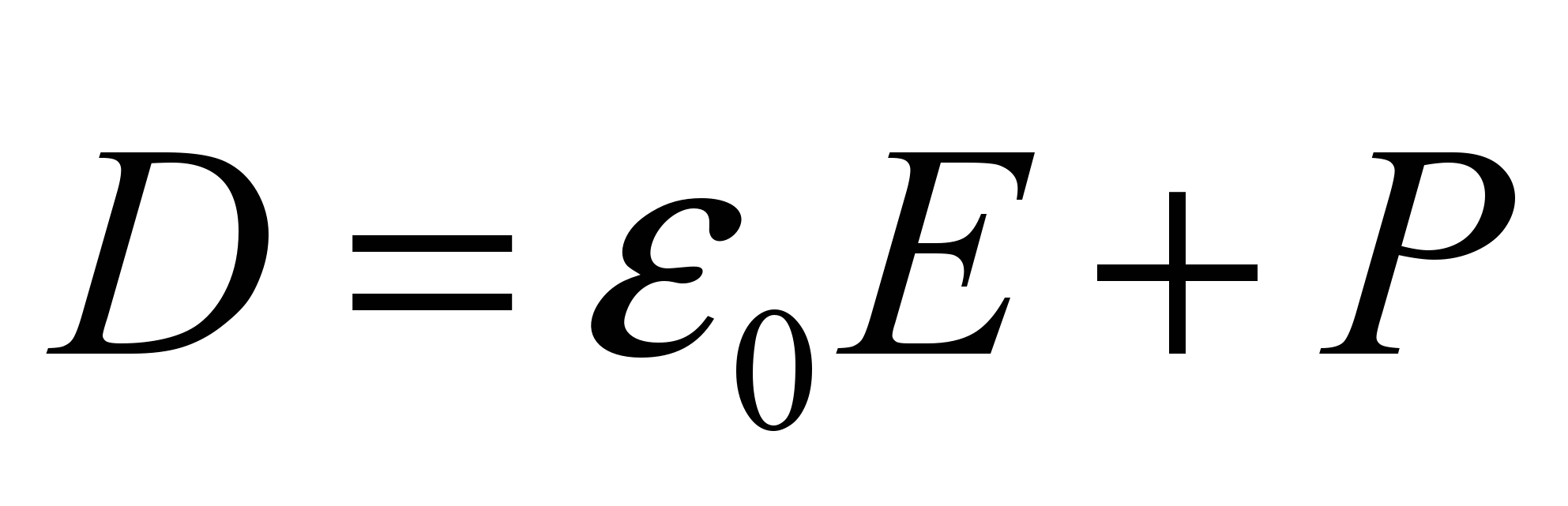      где Р – вектор поляризованности.

      Тогда плотность тока смещения
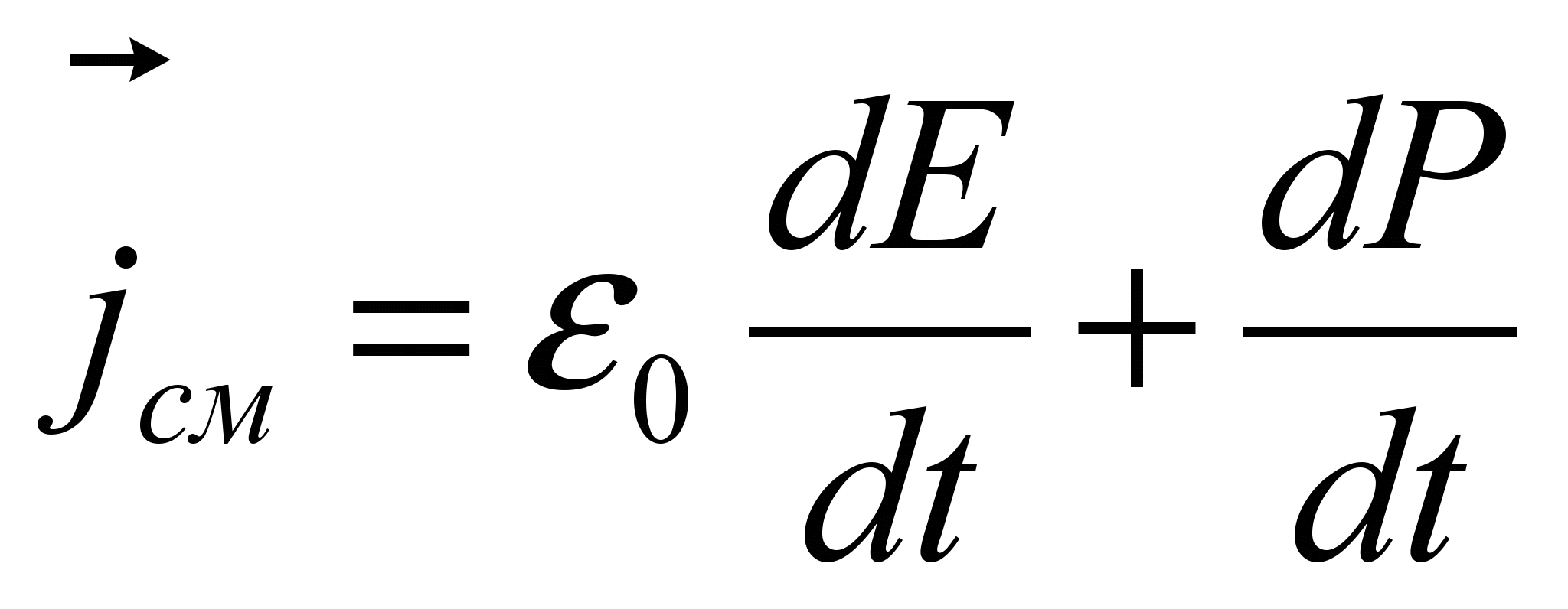      где 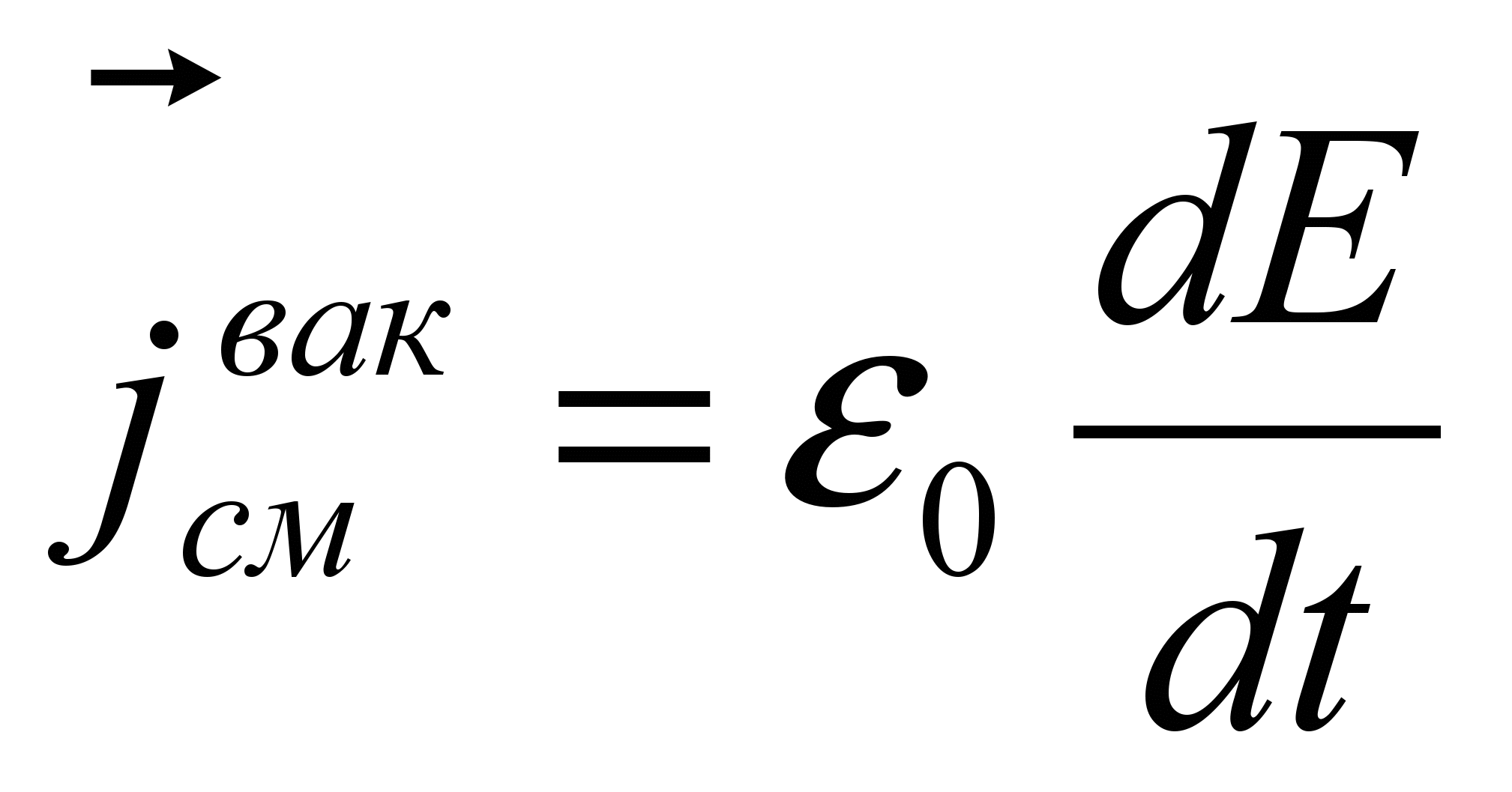– плотность тока смещения в вакууме, а 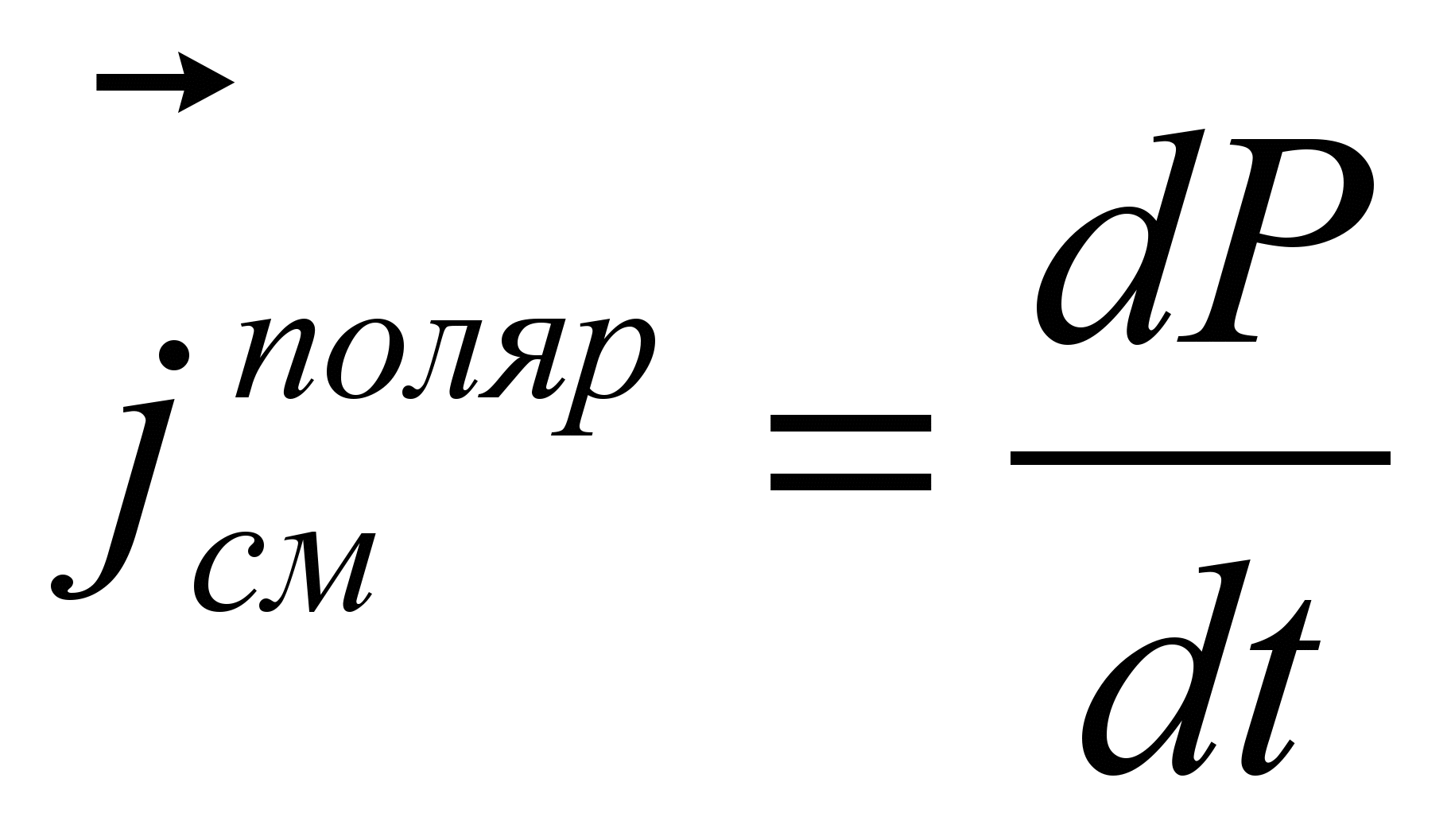– плотность тока поляризации (смещение зарядов в молекулах неполярных диэлектриков или поворот диполей полярных диэлектриков).

    1. Токи смещения не сопровождаются выделением теплоты.
    2. Второе уравнение Максвелла в интегральной форме имеет вид


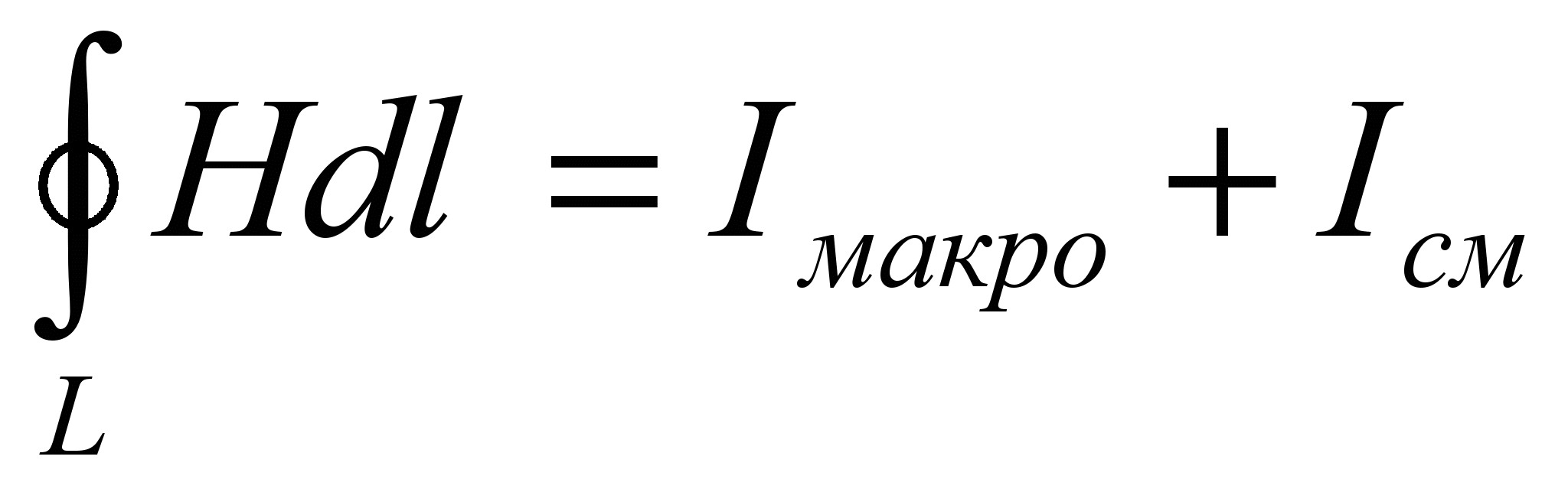
    1. По теореме Стокса 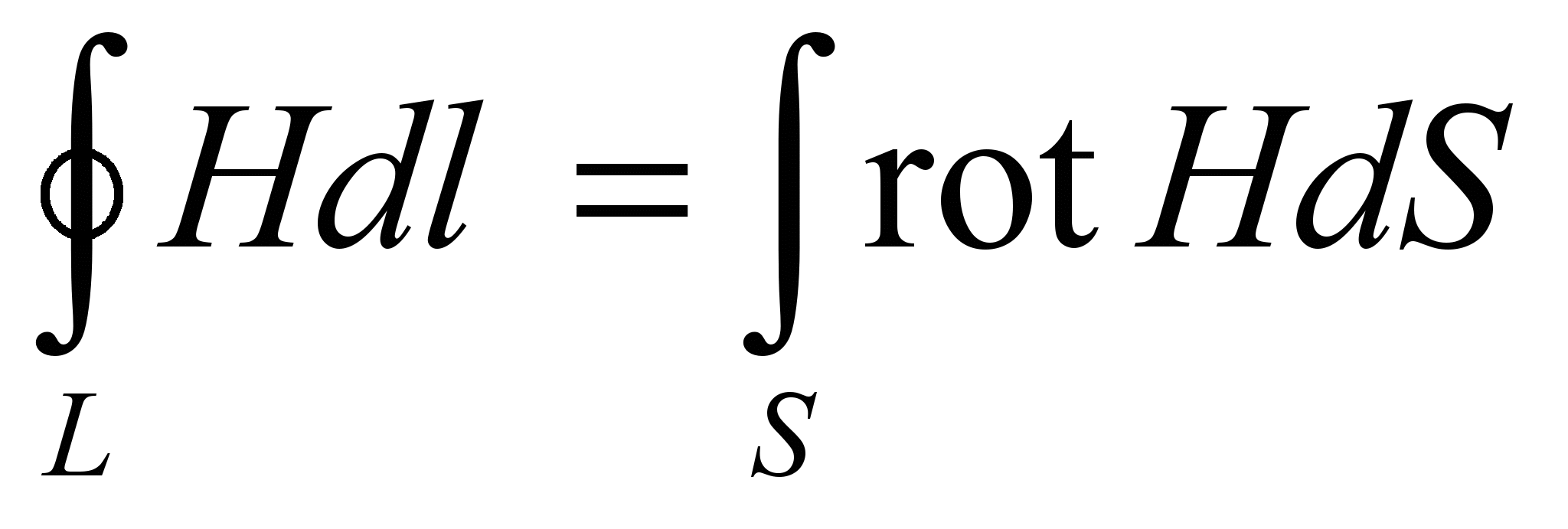,а полный ток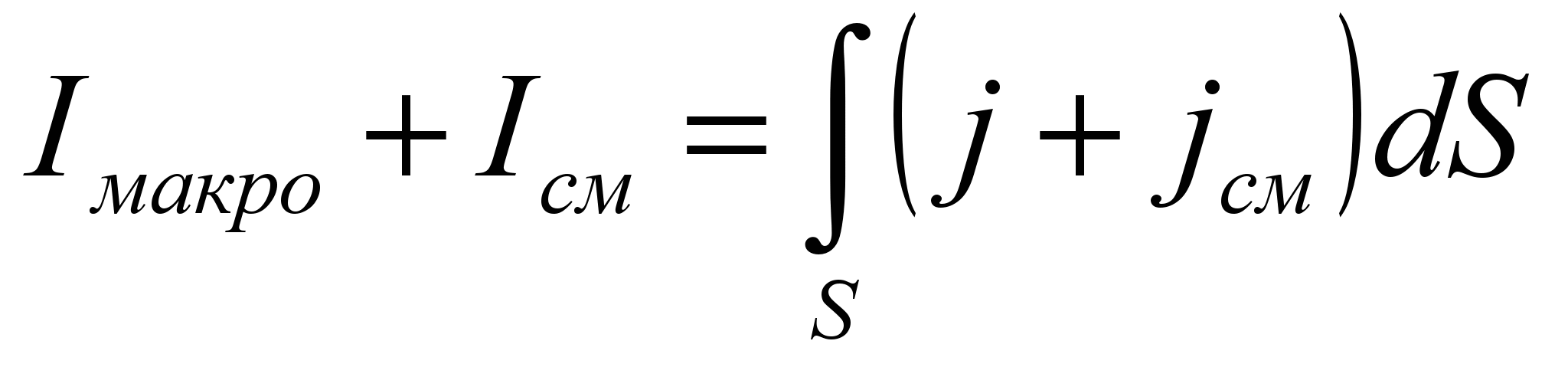

      вследствие чего в дифференциальном виде второе уравнение Максвелла имеет вид




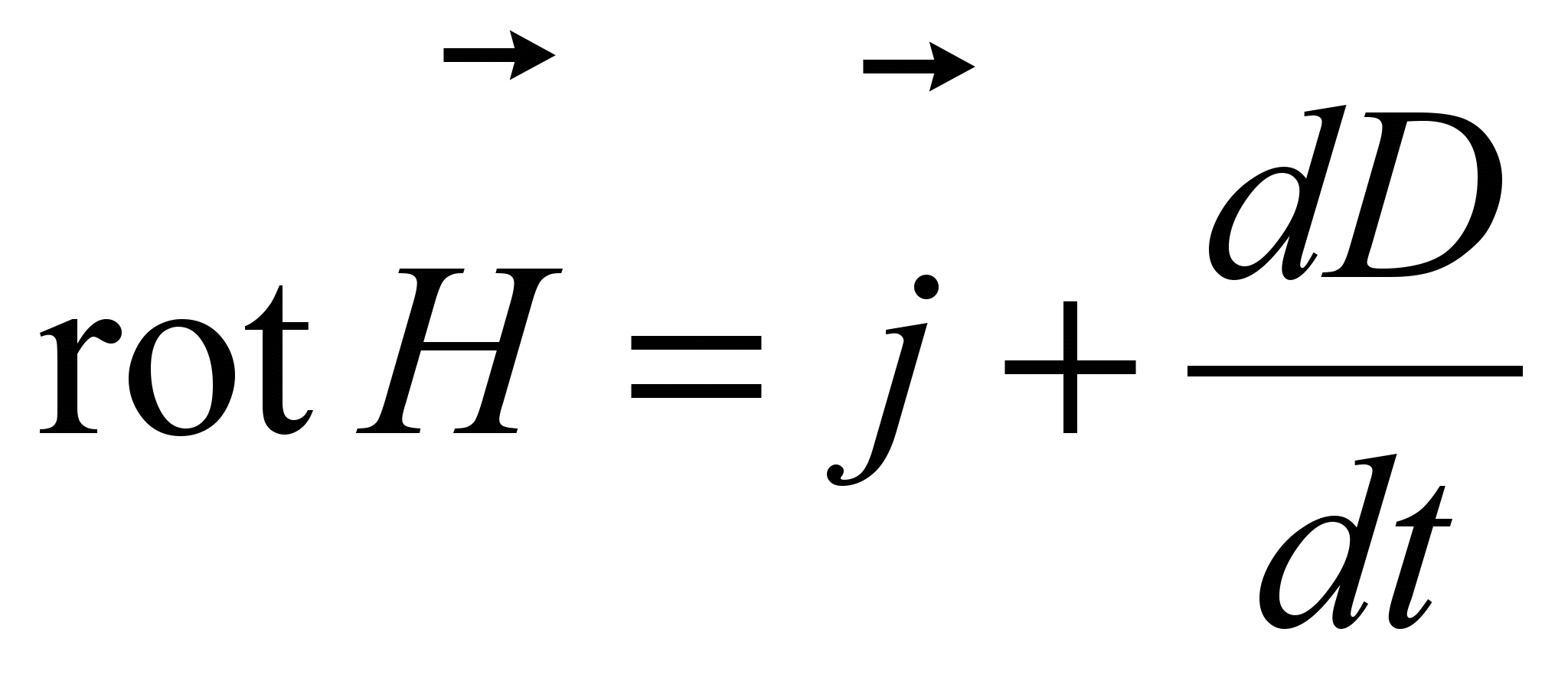
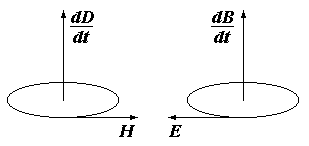
  1. Для областей поля, где нет макротоков

 

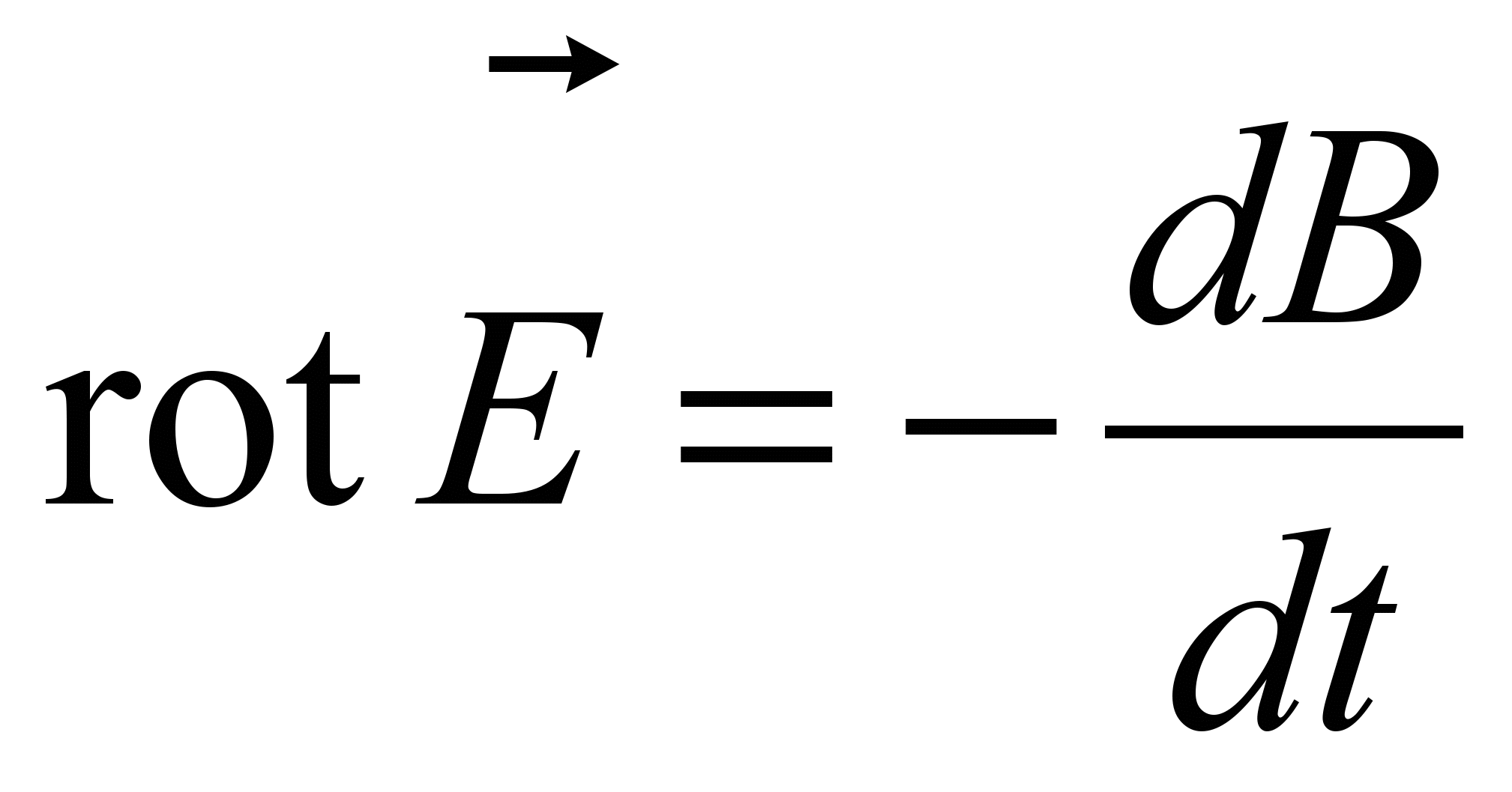
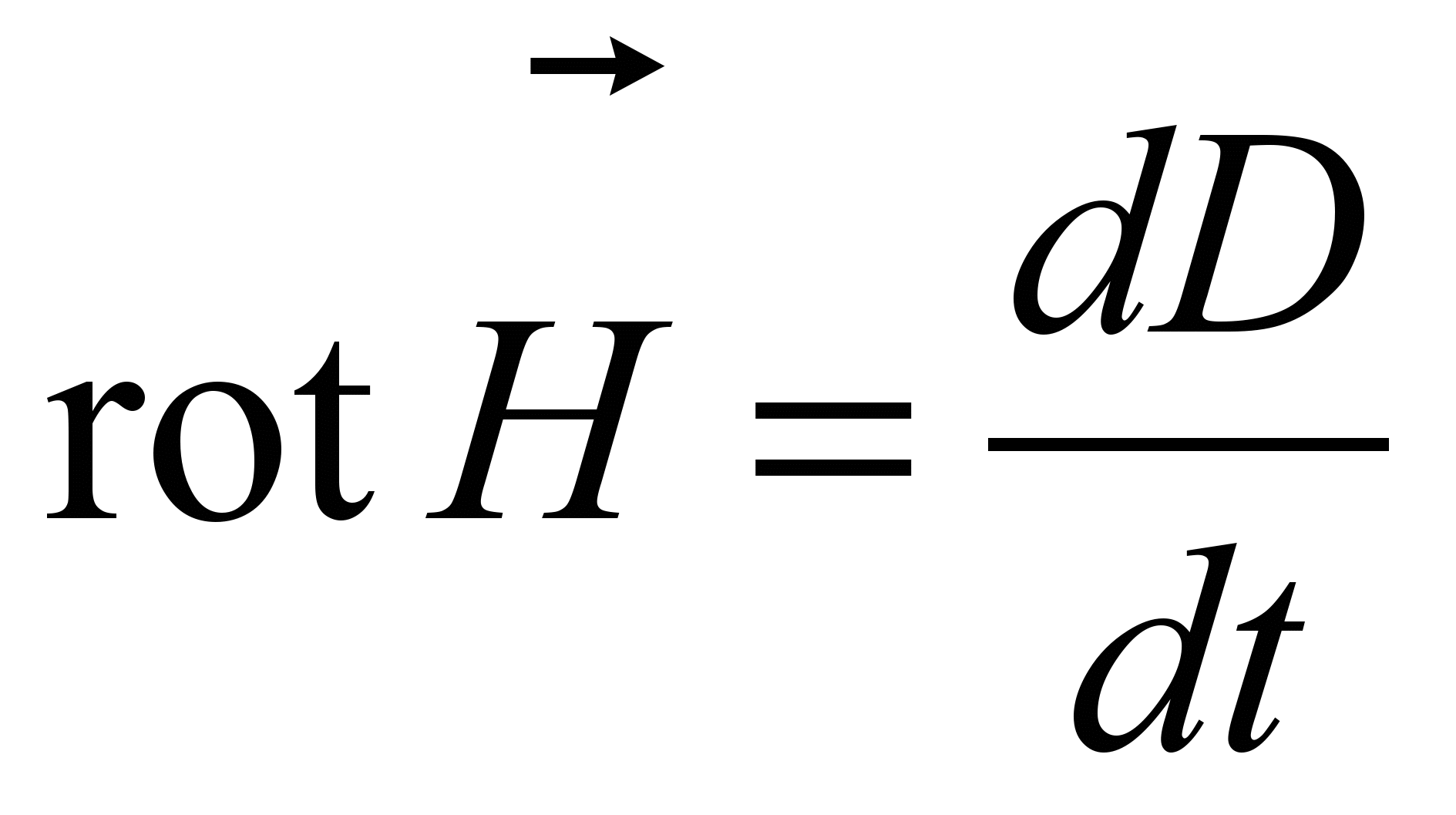
где знак минус в первом уравнении Максвелла означает, что вектора Н и dD/dt соответствуют правовинтовой системе, а вектора Е и dB/dt – левовинтовой.

4. ТЕОРЕМА ГАУССА И ПОСТУЛАТ МАКСВЕЛЛА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ

Максвелл обобщил теорему Гаусса - Остроградского для электростатического поля. Он предположил, что эта теорема справедлива для любого электрического поля, как стационарного, так и переменного. Соответственно, третье уравнение Максвелла в интегральной форме имеет вид: 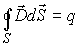. или 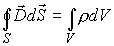. (18), где 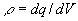- объемная плотность свободных зарядов, [ ρ] =Кл / м3

Из 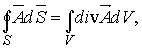следует, что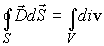 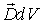. (19).Из сравнения (18) и (19) находим, что 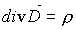. Четвертое уравнение Максвелла в интегральной и дифференциальной формах имеет

следующий вид: , .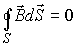

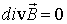5. Выражение в дифференциальной форме принципов непрерывности магнитного потока и непрерывности электрического тока.

Магнитный поток сквозь любую замкнутую поверхность равен нулю.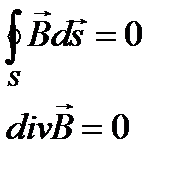

Линии тока нигде не прерываются и всегда являются замкнутыми.

Полный ток, (токи проводимости, переноса и смещения), проходящий сквозь любую замкнутую поверхность в направлении внешней нормали равен 0.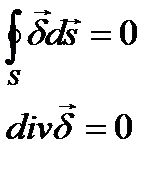

6. Полная система уравнений электромагнитного поля в дифференциальной форме.

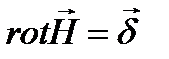
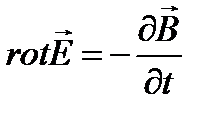
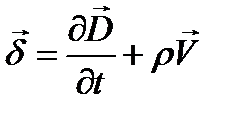
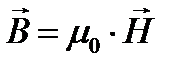
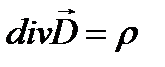
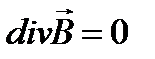
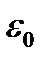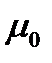Учитывая, что и постоянные величины получаем: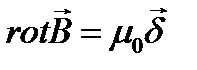

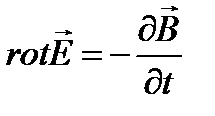
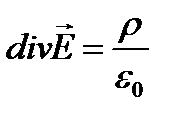
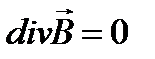
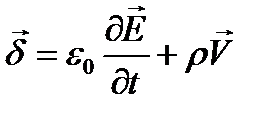
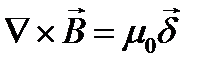
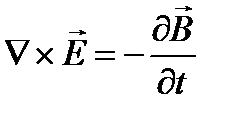
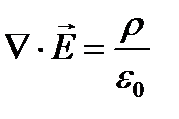
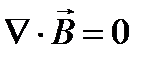
7. Электростатическое поле. Градиент электростатического потенциала.

Допустим, что положение т.А которой рассматривается потенциал φ определяется её расстоянием l от т.О вдоль некоторого пути до точки Р, где потенциал принят равным 0.

Выражение потенциала пишется в виде:

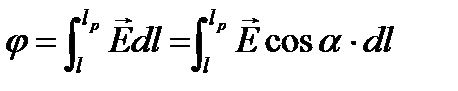
Где lp - длина всего пути от т.О до Р;

α – угол м/у направлением 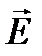и касательной к пути.

Возьмем частную производную от обоих частей равенства по нижнему пределу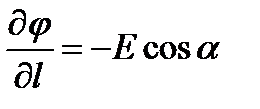

Приращение потенциала рассчитанное на единицу перемещения в каком либо направлении численно равно взятой с обратным знаком составляющей напряженности поля в этом направлении.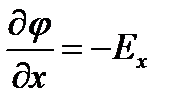

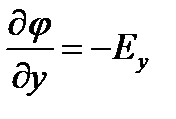
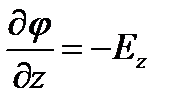
Линии напряженности поля нормальны к поверхности равного потенциала по координате имеет наибольшее значение в направлении нормальном к поверхности равной потенциалу и противоположным направлению вектора Е и называется градиентом электростатического потенциала ( gradφ)

Градиент потенциала равен приращению потенциала отнесенному к единице длины и взятому направлении, в котором это приращение имеет наибольшее значение.

Векторы Е и gradφ равны м/у собой по величине и направлены в противоположную сторону:

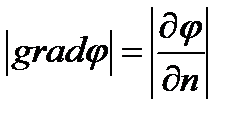
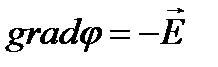
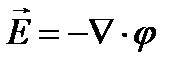
В декартовой системе координат: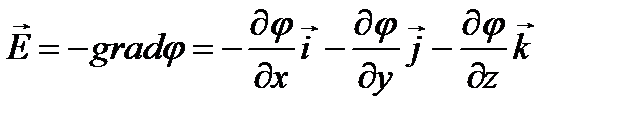

 

 

8. Уравнение Пуассона и Лапласа для электростатического поля

div =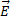

+ =

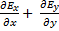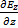Ex = 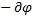/ 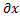, Ey = 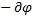/ 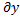, Ez = / ,

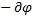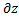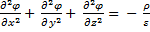- уравнение Пуассона

Интеграл φ = 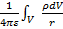- является решением уравнения Пуассона в случае, когда заряды распределены в конечной области пространства.

Если рассматриваемой области пространства отсутствуют объемные эл.заряды¸ то уравнение Пуассона примет вид:

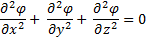
и называется в этом частном случае уравнением Лапласа.

Уравнение Лапласа можно записать в виде: 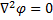∆φ = 0 ∆ ≡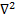

9. Уравнение Максвелла в комплексном виде. Волновое уравнение Гельмгольца

Объединим плотности тока проводимости и смещения:

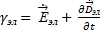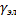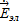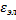
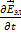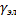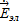= · + = · + jω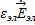

Тогда при изменении векторов поля во времени по гармоническому закону (в комплексной форме, как 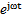), система уравнений Максвелла в комплексной форме может быть приведена к комплексному виду:

I. rot 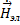= jω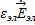

II. rot 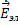= -jωμ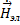

III. div 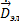= 0

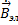IV. div = 0

Комплексная диэлектрическая проницаемость среды: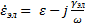

В этом случае волновые уравнения преобразуются в уравнения Гельмгольца:

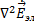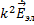+ = 0 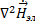+ 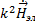= 0 k = ω 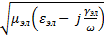комплексное волновое число.

11. Вектор Пойнтинга

Вектор Пойнтинга определяет направление и величину потока электромагнитной мощности, проходящей через единицу поверхности в направлении распространения волны.

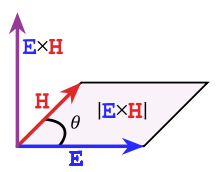Вектор плотности потока энергии электромагнитного поля:

В случае квазимонохроматических электромагнитных полей справедлива формула для усредненной по периоду комплексной плотности потока энергии:

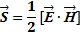
где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно. В этом случае чёткий физический смысл имеет только действительная часть комплексного вектора S — это вектор усреднённой за период плотности потока энергии. Физический смысл мнимой части зависит от конкретной задачи.

 

12. Вывод волновых уравнений непосредственно из уравнений Максвелла в дифференциальной форме

Рассмотрим вывод волновых уравнений непосредственно из уравнений Максвелла. Возьмем уравнение для ротора электрического поля, определяемого через производную по времени от магнитной индукции.

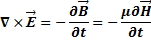
Векторно домножим это уравнение на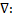

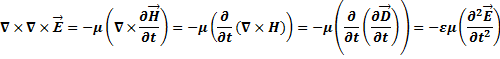
Так как дивергенция электрического поля в диэлектрической среде равна нуля, то в однородной среде дивергенция вектора 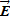тоже равна нулю, что следует из уравнения Максвелла.

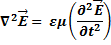
Волновое уравнение для электрической составляющей поля.

Рассуждая аналогичным образом можно получить волновое уравнение для магнитной составляющей поля.

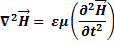
10. Основные свойства плоских электромагнитных волн

Плоской называют волну, распространяющуюся вдоль какой – либо линейной координаты и неизменную в каждый фиксированный момент времени в плоскости, перпендикулярной этой координате.

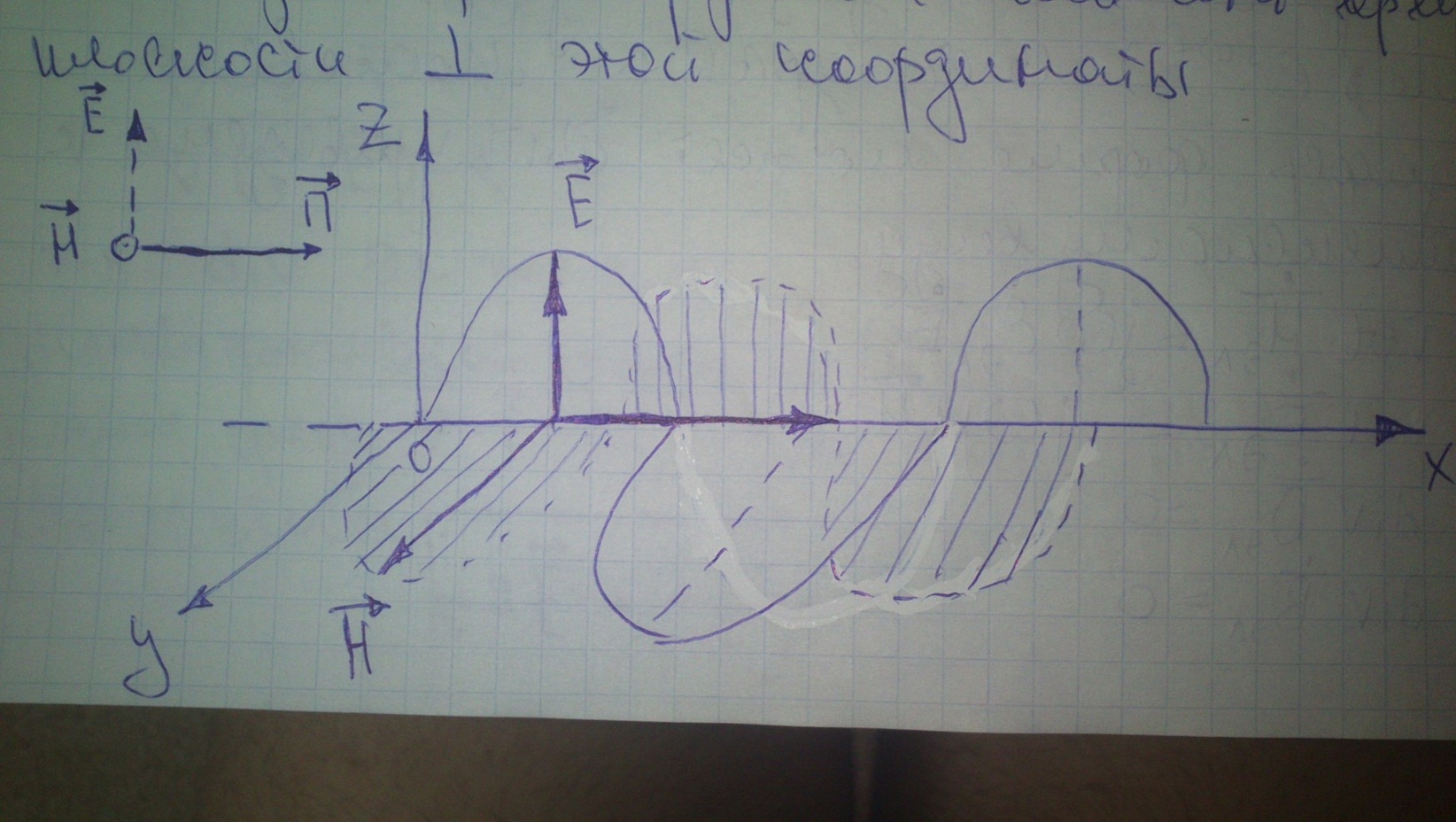Предположим, что плоская волна распространяется вдоль оси Х декартовой системы координат.

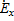= Еmxej(ωt-kz)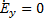 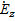= 0

Основные свойства и характеристики плоских волн:

1) Вектор напряженности эл.поля удовлетворяет волновому уравнению Гельмгольца:

2) 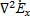= 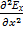+ + 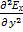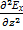= Еmxejωt 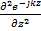= - k2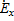

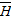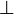
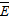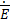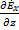
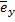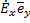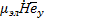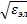3) Вектор напряженности магнитного поля перпендикулярен вектору напряженности эл.поля ( эл эл). Из 2ого уравнения Максвелла:rot = = - jk = - j𝜔 Emx = Нmy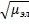

4) Отношение 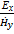- называется волновым или характеристическим сопротивлением среды. 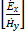= 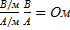Оно определяет связь между векторами эл.и магнитного поля в плоской волне. 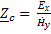= = 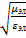= 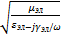|Z|ejφz

Волновое сопротивление среды последовательно – взаимная связь между векторами поля, определяется параметрами пространства, в котором распространяется плоская волна и частота самой волны.

Для проводимых сред: 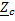= 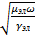ejπ/4, Т.е.в проводящих средах вектор напряженности эл.поля опережает вектор напряженности магнитного поля по фазе на угол π/4.

4) Комплексное волновое число:k = ω 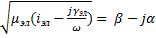, 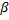- коэффициент фазы,α – постоянная затухания. Определяет характер изменения амплитуды и фазы, напряженности плоской волны с расстоянием Z. ,

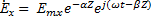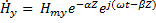
5) Фазовая скорость волны – скорость перемещения фронта волны, фиксированного значения фазы, вдоль направления распространения волны. ωt – βZ = const , v ф = dz/dt, ωdt – βdZ =0 v ф = dz/dt = ω/β

6) Длина волны 𝝀 – расстояние, на котором фаза волны изменяется на 2π: β𝝀 = 2π 𝝀 = 2π/β = v ф/f

7) 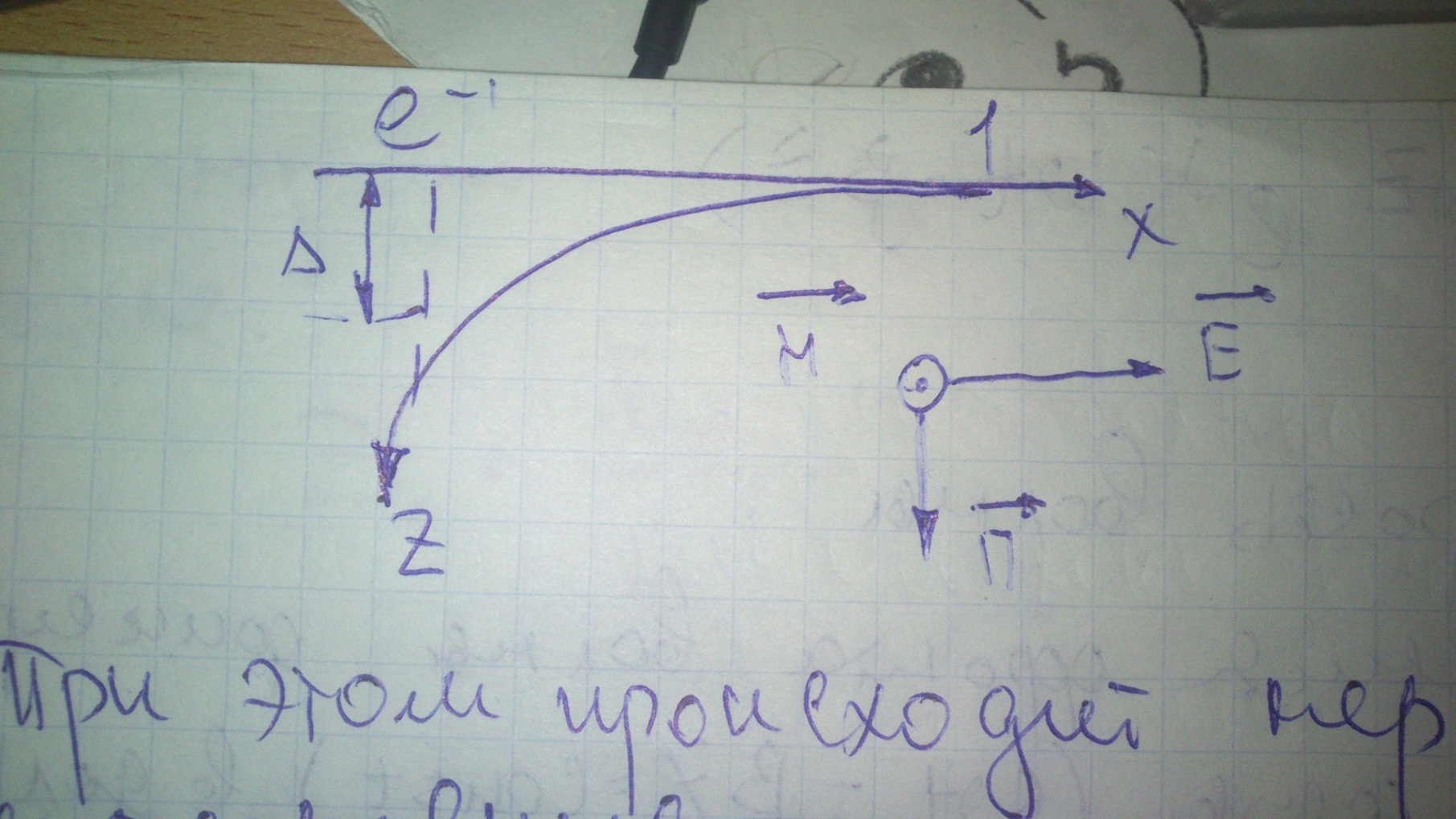Явление поверхностного эффекта заключается в неравномерном распределении переменного электромагнитного поля в проводящей среде из – за затухания электромагнитной волны.

 

При этом происходит неравномерное распределение плотности тока и магнитной индукции, в установившемся режиме эти величины имеют максимальное значение у поверхности проводника.

Расстояние, на котором амплитуда вектора 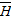эл или 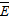эл волны в проводящих средах уменьшатся в е = 2,71 раз, называется глубиной проникновения.

∆ = ≈

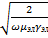
В большинстве случаев поверхностный эффект вреден, т.к.увеличивает эл.сопротивление переменному току и магнитное сопротивление переменному магнитному потоку. Поверхностный эффект может быть и полезен, например, в установках для индукционного поверхностного нагрева и закалки, а так же в электромагнитных экранах.

 

 

13. Численные методы расчета электромагнитных полей. Граничные условия

Среди численных методов наибольшее распространение получили: метод конечных разностей и метод конечных элементов.

Для расчетов применяют уравнение Пуассона:

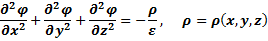
А так же уравнение Лапласа:

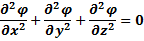
Решая задачи о потенциальном электрическом поле внутри некоторой области, недостаточно сказать, что поле должно удовлетворять в этой области уравнению Лапласа, но надо сообщить, например, какими электродами создается поле и какие потенциалы приданы электродам (граничные условия).

Метод сеток представляет собой числовой метод интегрирования дифференциальных элементов путем сведения их к уравнениям в конечных разностях.

 

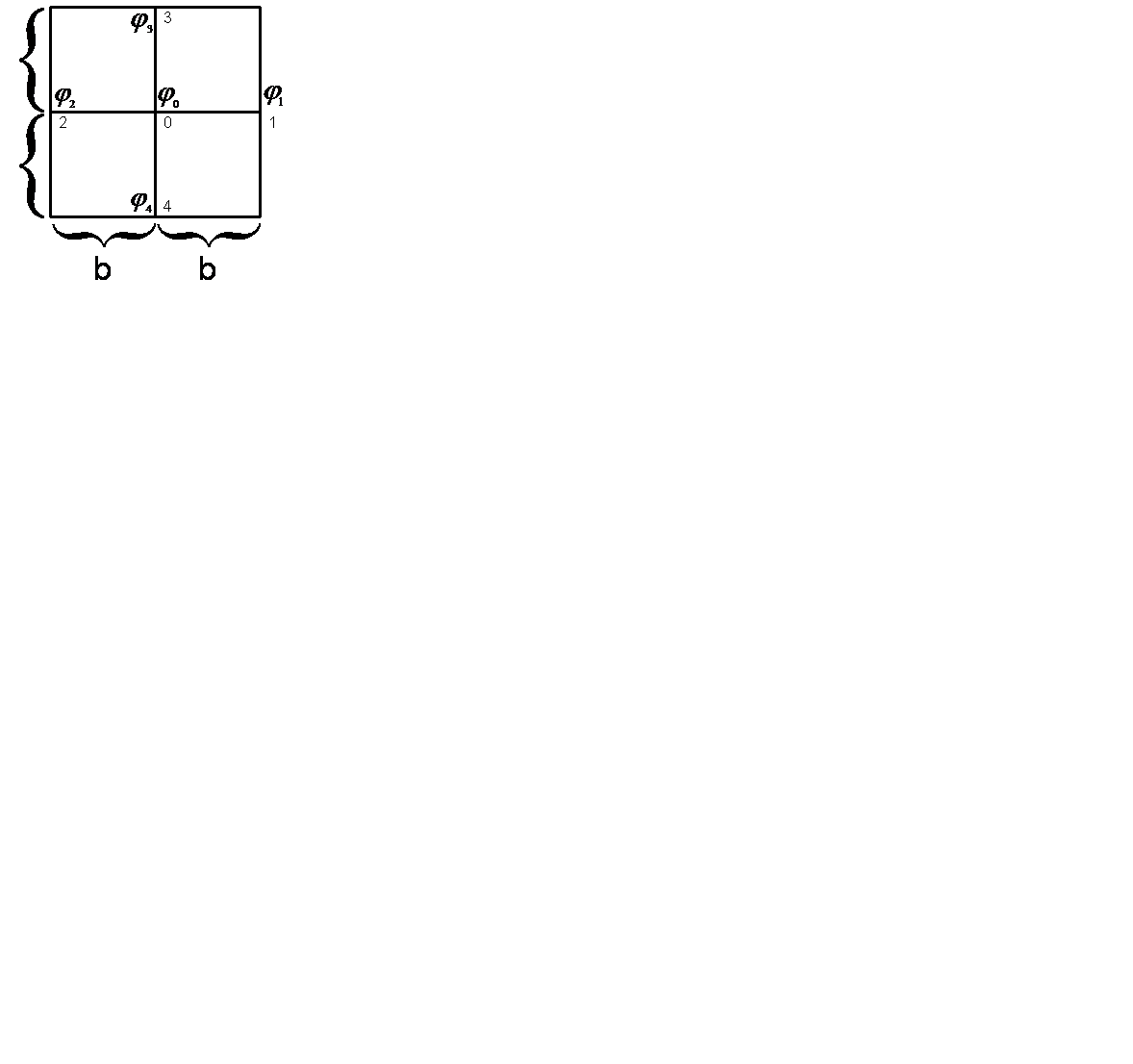Выведем приближенное соотношение между потенциалами сетки:

 

 

 

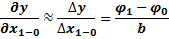
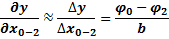
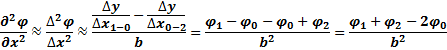
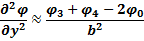
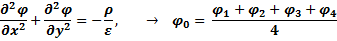
Чем меньше шаг сетки b, тем меньше погрешность от замены уравнений Пуассона или Лапласа на уравнения в конечных разностях. Применяют не только квадратные сетки, но и полярные.