III . Периодические несинусоидальные токи в электрических цепях.
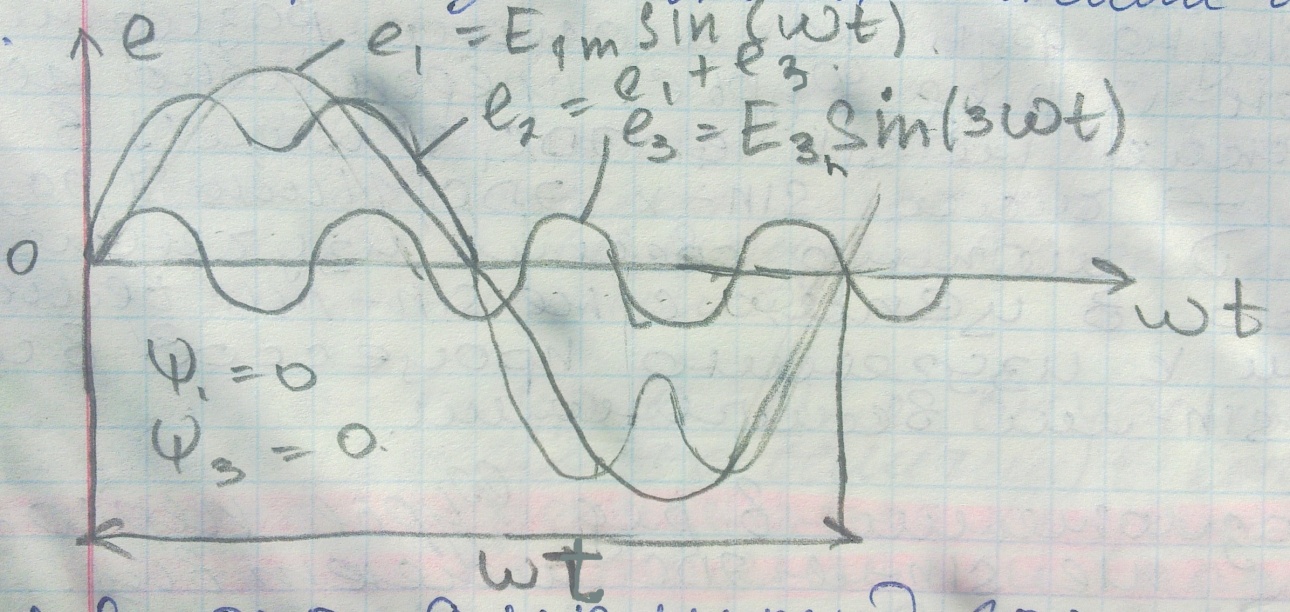 1. Основные понятия о несинусоидальных ЭДС, напряжениях, тока и методах анализа.
1. Основные понятия о несинусоидальных ЭДС, напряжениях, тока и методах анализа.
Для большинства эл.приёмников нормальный режим работы обеспечен синусоидальным напряжением подачи, всвязи с этим ГОСТ 13109 устанавливает нормы допустимого отклонения периодических ЭДС, напряжения и тока от синусоидальной формы.
В реальных условиях в эл.установках различного назначения возникать несинусоидальные токи, это может иметь место даже при подаче в цепь синусоидального напряжения. Например включение в цепь нелинейных элементов.
В реальных эл.цепях функции описывающие несинусоидальные ЭДС, напряжение, токи всегда удовлетворяют условиям Дирихле.
За полный период имеются конечное число разрывов 1-го рода и конечное число максимумов и минимумов. Такую функцию можно разложить в гармонический ряд Фурье, представив периодические несинусоидальные ЭДС, напряжение или ток в виде суммы бесконечного числа синусоидальных ЭДС, напряжения или токов различной частоты можно свести изучение процесса в цепях с несинусоидальными величинами к изучению процессов в цепях с синусоидальными величинами.
При разложении в ряд Фурье периодическая несинусоидальная ЭДС имеет вид:
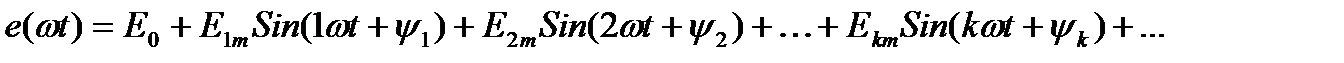
У каждой гармоники своя частота.
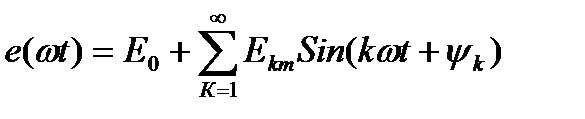 ,
, 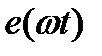 -Значение несинусоидальной ЭДС в момент времени t, Е0-Постояная составляющая ЭДС.
-Значение несинусоидальной ЭДС в момент времени t, Е0-Постояная составляющая ЭДС.
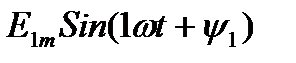 -Основная или 1-я гармоника, имеющая ту же частоту, что и несинусоидальная ЭДС
-Основная или 1-я гармоника, имеющая ту же частоту, что и несинусоидальная ЭДС
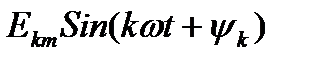 -Гармоника высшего порядка, имеющая частоту в К раз больше основной.
-Гармоника высшего порядка, имеющая частоту в К раз больше основной.
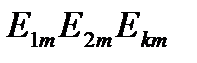 -Амплитуды гармоник 1-го, 2-го, К-го порядка,
-Амплитуды гармоник 1-го, 2-го, К-го порядка, 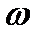 -угловая частота основной гармоники.
-угловая частота основной гармоники. 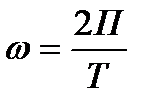 .
.
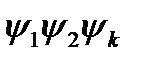 -Начальные фазы гармоник.
-Начальные фазы гармоник.
Амплитуды гармоник разного порядка зависят только от формы несинусоидальной кривой, а начальные фазы изменяются при изменении начала отсчёта времени. ( 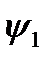 =0;
=0; 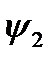 =0)
=0)
Для определения амплитуд гармоник целесообразнее её представить в виде суммы 2-х гармоник 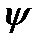 =0
=0 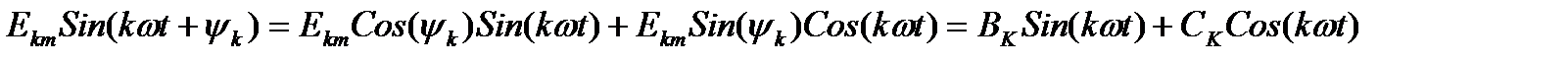 ;
;
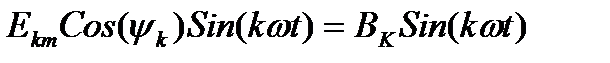 ;
; 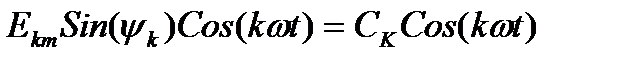 ;
;
Амплитуда гармонических колебаний ВК и СК зависят от начальных фаз и поэтому изменяются при изменении начального отсчёта времени. С учётом последнего выражения для ограниченного числа членов ряда выражение принимает вид: 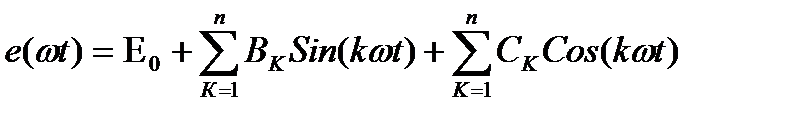 ;
;
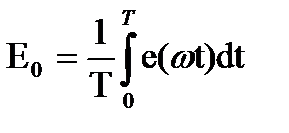 ;
; 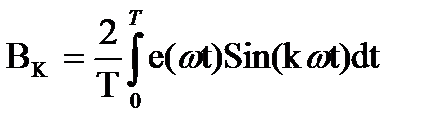 ;
; 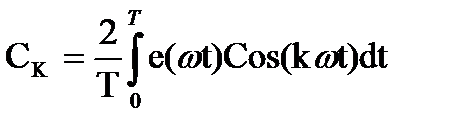 ;
;
Зная амплитуды двух слагаемых каждой гармоники можно найти полную амплитуду этой гармоники и её фазу:
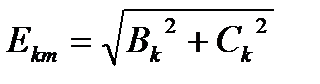 ;
; 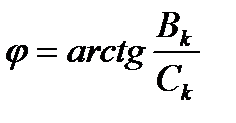 .
.
Постоянная составляющая Е0 является средним значением периодической несинусоидальной ЭДС. Аналогичным образом можно представить рядом Фурье несинусоидальные функции тока и напряжения.
2. Действующие и средние значения несинусоидальных электрических величин.
Измерительные приборы тепловой, эл.магнитной, эл.динамической, эл.статической систем показывают действующие значения измеряемых величин. Действующие значение несинусоидальных ЭДС (напряжения и тока), равно среднеквадратичному её значению за время равное её периоду:
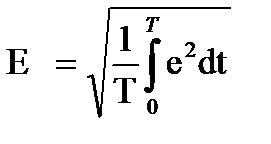 ;
; 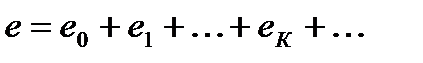 ;
; 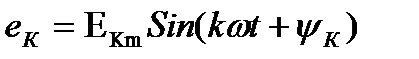 ;
;
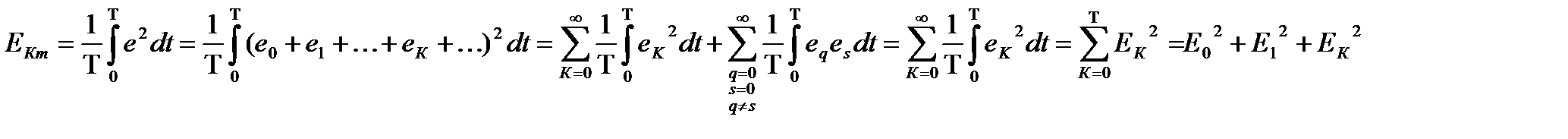 При
При 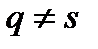
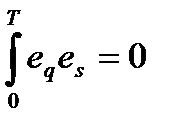 ;
;
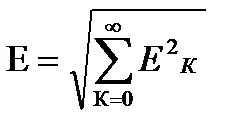 - аналогично для действительных значений тока и напряжения:
- аналогично для действительных значений тока и напряжения:
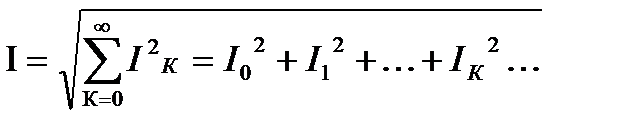 ;
; 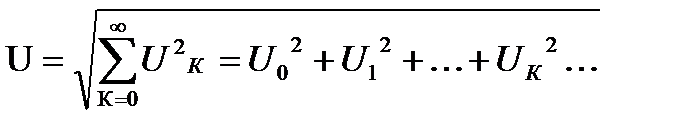 ;
;
Действующее значение несинусоидальной величины равно корню квадратному из суммы квадратов действующего значения и действующих значений её гармоник .
Эквивалентной синусоидальной величиной называют такую величину действующего значения, которая равна действующему значению несинусоидальной величины.
Амплитуда эквивалентной синусоидальной ЭДС определяется выражением: 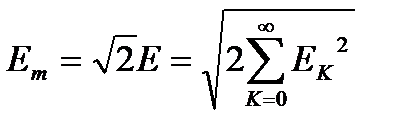 ;
;
Среднее значение за полупериод: 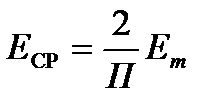 .
.
4. Анализ линейных электрических цепей при несинусоидальном напряжении источника питания.
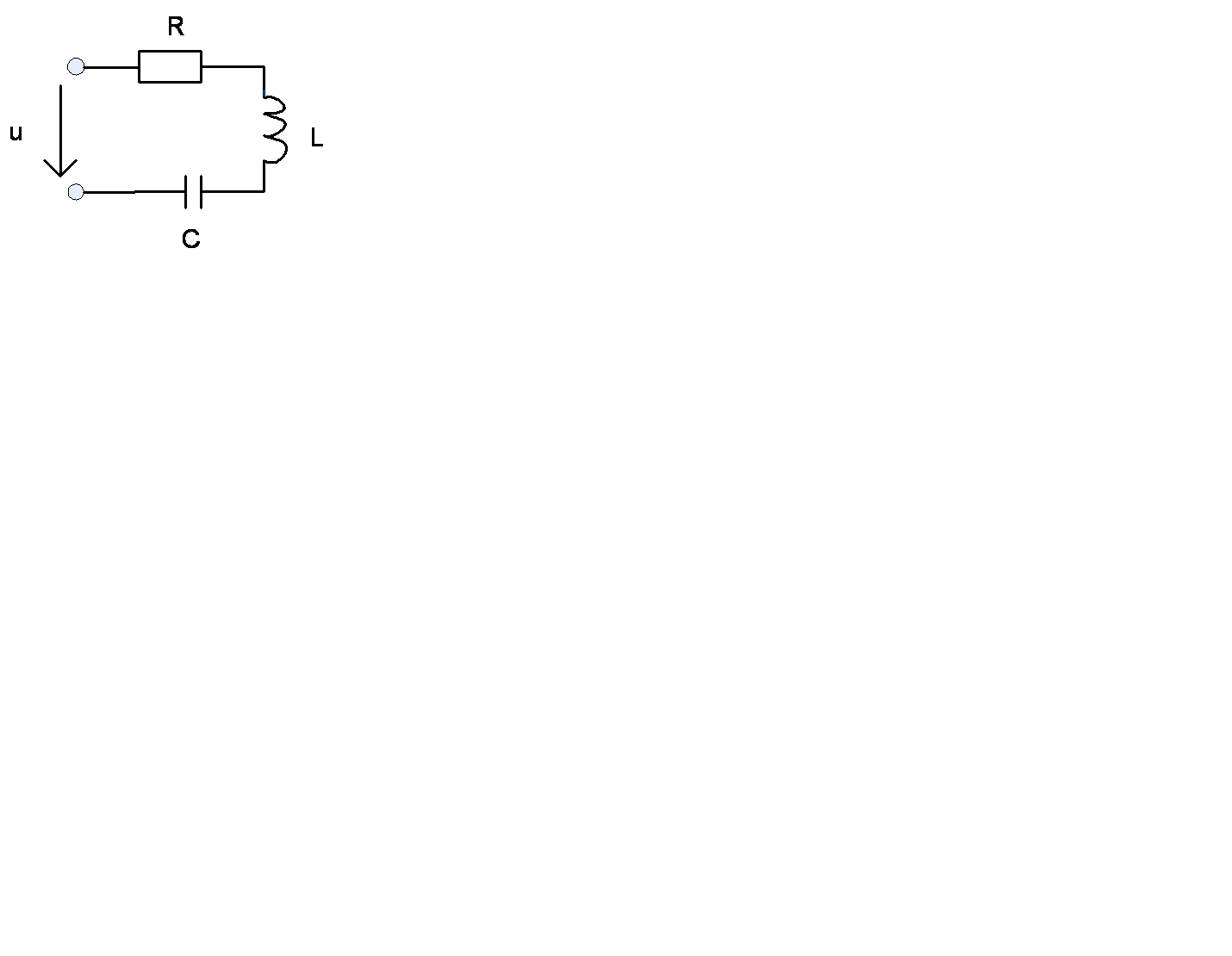
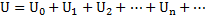
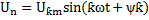
Так как цепь линейна то можно найти составляющую тока создаваемую каждой составляющей U –нием ,а суммарный ток найти сложением составляющих токов используя принцип наложения.
Постоянное состояние I не синусоидального тока может существовать только тогда ,когда в цепи нет C конденсатора.
Гармоника 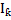 – порядка определиться:
– порядка определиться: 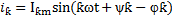
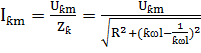 ,
, 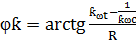
Далее по принципу: 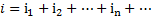
Полное сопротивление цепи для любой гармоники I зависит от порядка гармоники 
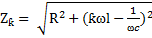 ,
, 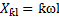 ;
; 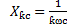
3. Активная мощность при несинусоидальных напряжении и токе.
Активная мощность определяется как средняя мощность за период.
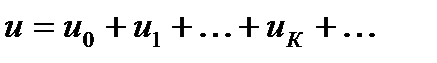 ;
; 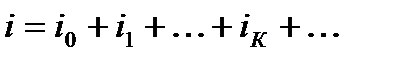 ;
;
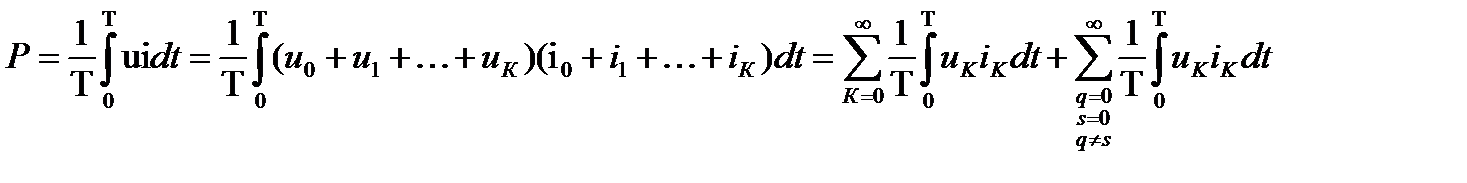 ;
;
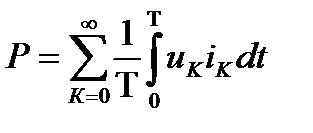 ;
; 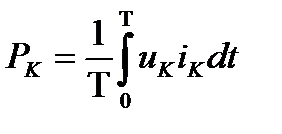 ;
;
Для активной мощности при несинусоидальном напряжении выражение представляет из себя сумму активной мощности каждой гармоники в отдельности.
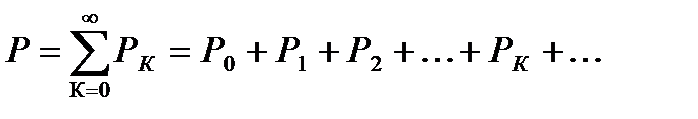 ;
; 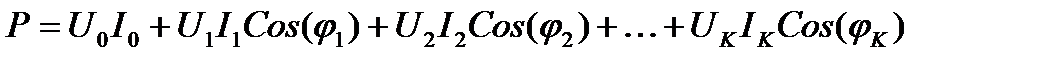 ;
;
К эл.цепям с несинусоидальными напряжением и током применимо понятие полной мощности, определяемой произведением действующих значением напряжения и тока S=UI.
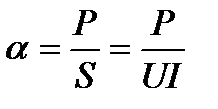 ;
; 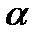 -коэффициент мощности для несинусоидальных напряжений и тока, Р-активная мощность, S-полная мощность.
-коэффициент мощности для несинусоидальных напряжений и тока, Р-активная мощность, S-полная мощность.
В отличие от эл.цепей синусоидального тока где коэффициент мощности цепи с активным сопротивлением равным 1, в цепях несинусоидальных напряжений и тока 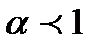 , даже для цепи с активным сопротивлением, зависящим от частоты и тока.
, даже для цепи с активным сопротивлением, зависящим от частоты и тока.
Допустим что ток в цепи синусоидальный, а ток содержит высшие гармоники: 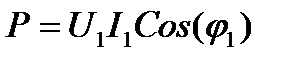 ;
; 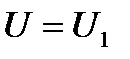 ;
; 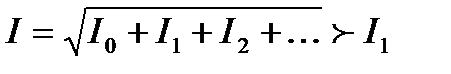
Действующее значение напряжения: 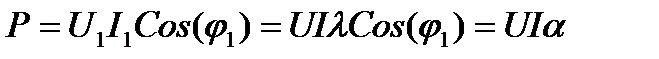 ;
;
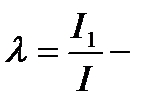 коэффициент искажения.
коэффициент искажения.
Так как 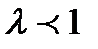 , то
, то 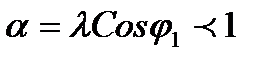 , в любом случае из этого следует что наличие высших гармоник в напряжении и токе почти всегда приводит к уменьшению коэффициента мощности, при замене несинусоидальных напряжений и тока эквивалентными величинами сдвиг фаз между ними определяется коэффициентом мощности -
, в любом случае из этого следует что наличие высших гармоник в напряжении и токе почти всегда приводит к уменьшению коэффициента мощности, при замене несинусоидальных напряжений и тока эквивалентными величинами сдвиг фаз между ними определяется коэффициентом мощности - 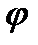 .
. 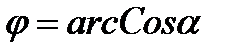 .
.
 4. Анализ линейных электрических цепей при несинусоидальном напряжении источника питания.
4. Анализ линейных электрических цепей при несинусоидальном напряжении источника питания.
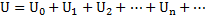
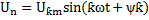
Так как цепь линейна то можно найти составляющую тока создаваемую каждой составляющей U –нием ,а суммарный ток найти сложением составляющих токов используя принцип наложения.Постоянное состояние I несинусоидального тока может существовать только тогда ,когда в цепи нет C конденсатора.
Гармоника 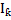 – порядка определиться:
– порядка определиться: 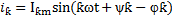 ,
,
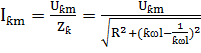 ,
, 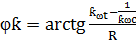 ,Далее по принципу:
,Далее по принципу: 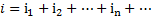
Полное сопротивление цепи для любой гармоники I зависит от порядка гармоники  :
:
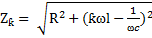 ,
, 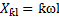 ;
; 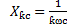
5. Несинусоидальные кривые с периодической огибающей. Биения
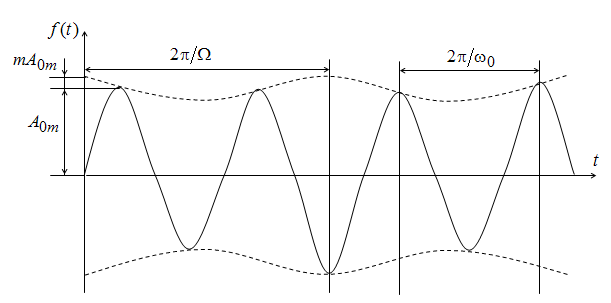
Это кривые, относящиеся к классу почти периодических. Они также разлагаются на гармонические составляющие. Период таких кривых обычно во много раз превышает период любой из составляющих и может стремиться к бесконечности. К числу явлений, характеризуемых такими кривыми, относятся биения и модуляции.
Биения. Простейший случай получается при сложении двух синусоид с равными амплитудами, но не равными частотами ω1 и ω2, причем ω1 > ω2: 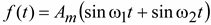
Преобразуя сумму синусов, получим 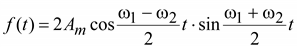
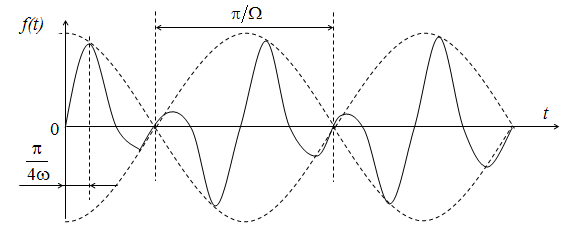 Можно считать, что кривая f(t) представляет собой синусоиду с угловой частотой
Можно считать, что кривая f(t) представляет собой синусоиду с угловой частотой 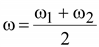 амплитуда которой изменяется по косинусоиде со значительно меньшей угловой частотой
амплитуда которой изменяется по косинусоиде со значительно меньшей угловой частотой 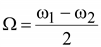 , тогда
, тогда
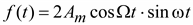
Частотой биений - частота 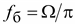 , равная числу максимумов огибающей кривой в единицу времени.
, равная числу максимумов огибающей кривой в единицу времени.
Пример несинусоидальной кривой с периодической огибающей показан на рис.1.
Период биений 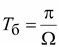 в общем случае не равен периоду кривой f(t).
в общем случае не равен периоду кривой f(t).
Модулированные колебания. Синусоидально изменяющаяся величина f(t) = 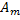 sin(ω t + Ψ) задается тремя параметрами: амплитудой
sin(ω t + Ψ) задается тремя параметрами: амплитудой 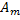 , угловой частотой ω и начальной фазой Ψ. Эти величины не зависят от времени. Однако для передачи различного рода сигналов применяются генераторы, в которых одна из этих величин изменяется по некоторому заданному закону. Изменение во времени одного из параметров
, угловой частотой ω и начальной фазой Ψ. Эти величины не зависят от времени. Однако для передачи различного рода сигналов применяются генераторы, в которых одна из этих величин изменяется по некоторому заданному закону. Изменение во времени одного из параметров 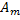 , ω или Ψ называют модуляцией. Различают амплитудную, частотную и фазовую модуляции.
, ω или Ψ называют модуляцией. Различают амплитудную, частотную и фазовую модуляции.
Пусть функция, изменяющаяся с частотой 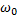 и амплитудой
и амплитудой 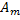 (t), модулирована гармоническим сигналом с частотой Ω <
(t), модулирована гармоническим сигналом с частотой Ω < 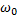 относительно среднего значения
относительно среднего значения 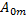 , т.е. с законом изменения
, т.е. с законом изменения 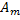 (t) (рис.8.2):
(t) (рис.8.2):
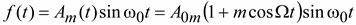
Частота 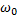 называется несущей частотой, частота Ω – модулирующей частотой, m – коэффициентом модуляции.
называется несущей частотой, частота Ω – модулирующей частотой, m – коэффициентом модуляции.
При определении токов или напряжений модулированные по амплитуде колебания могут быть разложены на синусоидальные составляющие: 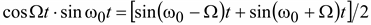
Тогда
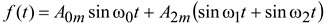 , где
, где 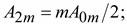
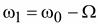 ;
; 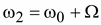
Таким образом, простейшие модулированные по амплитуде колебания могут быть представлены в виде суммы трех синусоидальных колебаний с несущей частотой 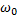 , боковыми частотами
, боковыми частотами 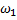 ,
, 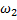 и постоянными амплитудами.
и постоянными амплитудами.
Под действующим значением колебаний с периодической огибающей, описываемых функцией 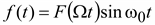 , обычно понимают действующее значение огибающей, деленное на
, обычно понимают действующее значение огибающей, деленное на 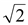
| Этим выражением можно пользоваться, если исследуется непериодический процесс за достаточно больной промежуток времени |
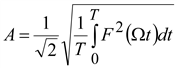 , где T = 2π/Ω.
, где T = 2π/Ω.
.
| 6.Резонанс в цепи несинусоидального тока. |
В цепях несинусоидального тока резонансные режимы возможны для различных гармонических составляющих. Как и при синусоидальных токах, резонанс на к-й гармонике соответствует режиму работы, при котором к-е гармоники напряжения и тока на входе цепи совпадают по фазе, иначе говоря входное сопротивление (входная проводимость) цепи для к-й гармоники вещественно.
Пусть имеет место цепь на рис. 1,а, питающаяся от источника несинусоидальной ЭДС, в которой емкость конденсатора может плавно изменяться от нуля до бесконечности.
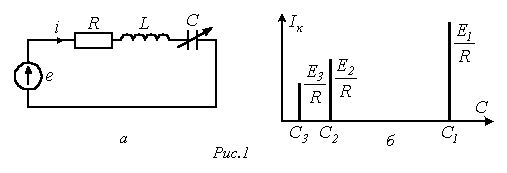 Для к-й гармоники тока можно записать Для к-й гармоники тока можно записать 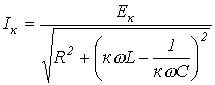 ,где ,где 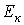 - действующее значение к-й гармоники ЭДС.
Таким образом, при изменении С величина к-й гармоники тока будет изменяться от нуля при С=0 до - действующее значение к-й гармоники ЭДС.
Таким образом, при изменении С величина к-й гармоники тока будет изменяться от нуля при С=0 до 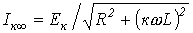 при при 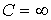 , достигая максимума , достигая максимума 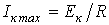 при резонансе (рис. 1,б), определяемом величиной емкости при резонансе (рис. 1,б), определяемом величиной емкости 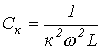 .
Следует отметить, что, несмотря на то, что обычно с ростом порядка гармонической ЭДС ее амплитуда уменьшается, в режиме резонанса для к-й гармонической ее значение .
Следует отметить, что, несмотря на то, что обычно с ростом порядка гармонической ЭДС ее амплитуда уменьшается, в режиме резонанса для к-й гармонической ее значение 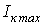 может превышать величину первой гармоники тока.
Резонансные явления используются для выделения гармоник одних частот и подавления других. Пусть, например, в цепи на рис. 2 необходимо усилить q-ю гармонику тока на нагрузке и подавить р-ю. может превышать величину первой гармоники тока.
Резонансные явления используются для выделения гармоник одних частот и подавления других. Пусть, например, в цепи на рис. 2 необходимо усилить q-ю гармонику тока на нагрузке и подавить р-ю.
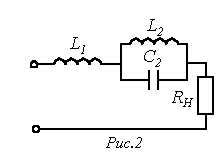 Для подавления р-й гармоники в режим резонанса токов настраивается контур Для подавления р-й гармоники в режим резонанса токов настраивается контур 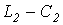 : : 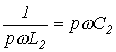 .
Для выделения q-й гармоники вся цепь для нее настраивается в режим резонанса напряжений: .
Для выделения q-й гармоники вся цепь для нее настраивается в режим резонанса напряжений:
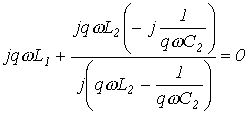 ,откуда при известных ,откуда при известных 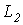 и и 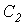 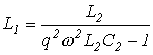 .
Отметим, что рассмотренные явления лежат в основе работы L-C -фильтров. .
Отметим, что рассмотренные явления лежат в основе работы L-C -фильтров.
|
7. Высшие гармоники в трехфазных цепях.
В трехфазных цепях кривые напряжения фаз B и C обычно воспроизводят форму кривой фазы A.
UА=f(t)
UB=f(t-T/3)
UC= f(t+T/3)
Рассмотрим гармоники K-ого порядка во всех трех фазах:
UАK=UKMsin(Kωt+ 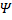 K)
K)
ωt=2 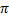
UBK= UKMsin(Kωt+ 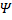 K-
K- 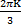 )
)
UCK=UKM(Kωt+ 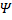 K+
K+ 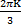 )
)
Следов-но напряж. гармоник,порядка кратного 3, K=3n n 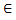 Z во всех фазах в момент времени имеет одно и тоже значение и направление
Z во всех фазах в момент времени имеет одно и тоже значение и направление
при K=3n+1 гармоники трех фаз образуют симметрич. сис-му U последовательность которых совпадает с последовательностью фаз первой гармоники.
при при K=3n+2 гармоники трех фаз образуют симметрич. сис-му U последовательности обратной основной.
Таким образом гармоники порядка 1,4,7,10 обр-т сис-му U прямой последовательности
гармоники порядка 2,5,8,11 обр-т сис-му U обратной последовательности
гармоники порядка 3,6,9,12 обр-т сис-му напряжений нулевой последовательности
При наличии постоянной составляющей в напряжении каждой из фаз она может рассматриваться как нулевая гармоника порядка кратного 3,т.е. образующая нулевую последовательность.
Если фазы генератора соединены звездой, то при несинусоид. фазном U, линейные U не содержат гармоник порядка кратных 3,т.к. они образуют сис-мы нулевой послед-ти.
Uф= 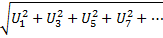
UЛ= 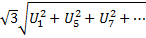
UЛ< Uф* 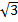
Ток в нейтральном проводе
IN=3 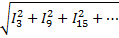
n=3*1 n=3*3 n=3*5
При отсутствии нейтральн. провода токи в каждой из фаз не могут содерж. высших гармоник порядка кратного 3.
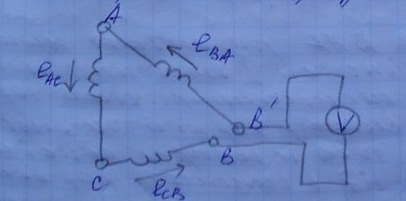
Если фазы генератор. соеденин. треу-ком, то при несинусоид. ЭДС,сумма ЭДС,действ. в замкн. контуре генератора не равно 0,а равна 3-ой сумме высших гармоник, порядка, кратного 3.
Вольтметр измерит гармоники ЭДС ,порядка кратн. 3 т.к. остальные в сумме дадут 0.
U=3 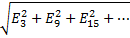
ЭДС гармон. порядка кратн. 3 вызыв. внутренний ток в генераторе.
Фазное U линейному
Uф= 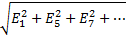 IФ=3
IФ=3 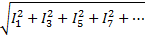
Линейный ток во внешней цепи.
Iл= 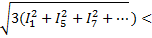 IФ*
IФ* 
Открытый треугольн. с ЭДС содерж. высшие гармоники примен. как утроитель частоты во внешн. цепи,подключ. к генератору обмотки кот. соедин. треугольн. токи не содержат гармон. порядка кратного 3.
IV . Цепи (линии) с распределенными параметрами.
1. Направляющие сис-мы передачи электроэнергии и их модели.
Электротехн. устр-ва предназн. для выработки и преобразов. эл. энергии. Электрические сигналы служащие носителями энергии необходимо передавать от одного устр-ва к другому из одной области простр. в другую. Для этого служат различные виды передающих сис-м:
1)Радиоприемник(передача электр. волн в неогран. среде)
2)Направляющие линии передач
3)В электроэнергетики используют проводные линии передачи низкой промышл. частоты
4)В информационных сис-х применяют оптические и диэлектрические волноводы, кабельные и проводниковые линии связи.
Решение задачи распространения электром. энергии по направл. сис-м базируется на ур-нях электродинамики(ур-е Максвела).
В диапазоне работы большинства пром. линий связи при частотах f<108 Гц в основном справедливо квази-статическое приближение и можно использовать эквивалент. электр. схемы.
В проводных линиях связи длина линии может быть соизмерима с длиной волны, но поперечные размеры линии существ. меньше в таких линиях токи и напряжения для одного и того же момента времени различн. в разных сечениях и необходимо учитывать изменение их значения вдоль линии.
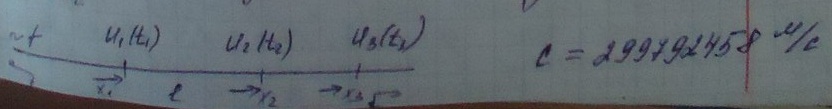
К распредел. цепям относятся не только проводн. линии,но и электротехнические устройства ,в которых требуется учитывать распределение U и I вдоль координат,например многоветк. обмотки эл. машины.
Обмотку трансформатора можно считать цепью с распред. параметрами только при большой частоте прилож. U либо импульса U.Ток в такой цепи изменяется по длине обмотки от витка к витку и ее следует рассматривать как эл. цепь с распредел. вдоль цепи продольн. и поперечными сопротивл.
Цепью с распредел. параметрами называют устр-во,в котором величина тока или магнитного потока изменяется вдоль длины и зависят от двух переменных времени и расстояния.
Любые электр. и магнитн. цепи с распредел. параметрами могут быть нелинейн. и линейн. однородн. и неоднородн.i(t,e), Ф(t,e), U(t,e)
Однородной называют цепь с распределительными параметрами при условии, что одинаковые все продольные U и поперечные проводимости идентичных участков устройства.
Электрические линии связи и передача электроэнергии имеют различные конструктивные исполнения:
1)Коаксиальный кабель 2)Триоаксиальный кабель 3)Плоский многожильный кабель
4)Многопроводная ВЛ связи 5)Трехфазная линия электропередачи энергии
 2. Уравнение двухпроводной линии
2. Уравнение двухпроводной линии
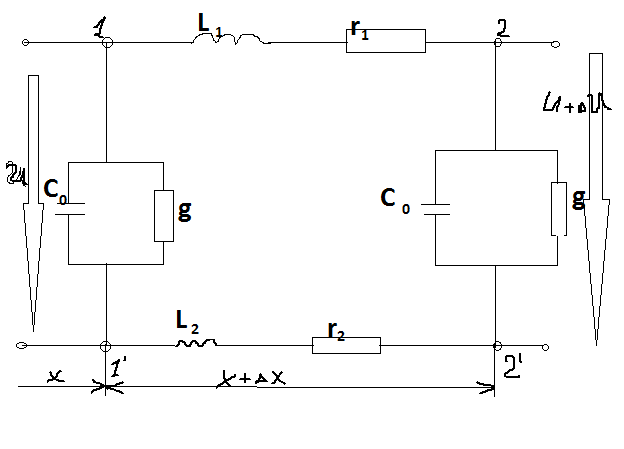
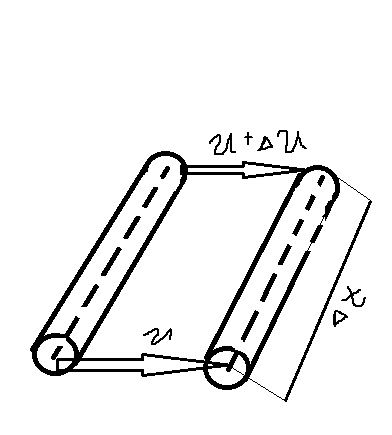 Процесс распространения эл. энергии вдоль однородной симметричной системы из 2 проводов. Выделим отрезок достаточной малой длины и представим его эквивалентной схемой участка.
Процесс распространения эл. энергии вдоль однородной симметричной системы из 2 проводов. Выделим отрезок достаточной малой длины и представим его эквивалентной схемой участка.
r-сопротивление тепловых потерь в проводах на единицу длинны(Ом\м), L-связанные внеш. И внутр. Индуктивностями проводов (Гн\м),g – проводимость потерь в диэлектрике(См\м), С – емскость учитывающая ток смещения между проводами(Ф\м).
Предположим, что по проводам протекает син. Ток не слишком высокой частоты (50Гц). Энергия входящая в провод идет на нагревание проводов и образование маг. Поля. Изменяющиеся маг. И эл. поля в диэлектрике отраженна погонной емкостью.
Наличие продольных сопротивлений и поперечной проводимости приводит к тому, что на участке длинной ΔХ получим приращение тока i +Δ i , U +Δ U .Δ i = 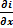 Δx ; ΔU =
Δx ; ΔU = 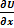 Δ x . Из ур-ий Кирхгофа для контура 1-2-2`-1`-1 узла 2 получим систему уравнений относительно приращений U,i:
Δ x . Из ур-ий Кирхгофа для контура 1-2-2`-1`-1 узла 2 получим систему уравнений относительно приращений U,i: 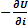 = r 0 i + L 0
= r 0 i + L 0 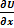 ; -
; - 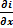 = g 0 U + C 0
= g 0 U + C 0 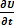 ; r 0 = r 1 + r 2 – погонное продольное сопротивление,
; r 0 = r 1 + r 2 – погонное продольное сопротивление, 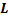 0 = r 1 + L 1- индуктивная линия.
0 = r 1 + L 1- индуктивная линия.
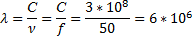
3.Уравнения многопроводных линий
Участок трехпроводной линии ,имеющий 2 прямых провода(1 и 2) и один обратный (0), содержит погонные элементы, отражающие электрические процессы. В общем случае к+1 проводной линии (к прямых проводов и 1 обратный) можно записать матричное соотношение
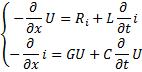
i и U – векторы токов и напряжений, R- диагональная матрица погонных сопротивлений, L,G и C- матрицы собственных и взаимных погонных индуктивностей, проводимостей и емкостей.
Погонные параметры применяемых линий являются паспортными параметрами и приводятся в справочниках. При расчетах необходимо учитывать зависимость погонных параметров от конструктивных и электрофизических. Указанные соотношения могут быть получены только из решений соответствующей краевой электродинамической задачи.
В зависимости от соотношения параметров для линии наряду с полной моделью возможно использование упрощенных моделей:
1)линия без потерь r0=0, g0=∞
2)резистивно-емкостная линия g0=∞, L0=0
3)Резистивная линия С0=0, L0=0
4.Расчет процессов в цепях с распределенными параметрами.
Система уравнений с начальными и граничащими условиями описывает процессы в цепях с распределенными параметрами.
В классическом подходе систему уравнений сводят к 1-му уравнению 2-го порядка, исключив переменную,например,ток.
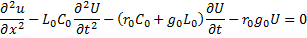
Начальные и граничные условия так же необходимо формулировать для напряжения u(t,x).
Процессы в линии без потерь(r0=0, g0=∞) описывают одномерным волновым уравнением.
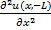 +
+ 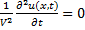 , V=-
, V=- 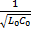 - скорость распространения волны
- скорость распространения волны
Его решение - совокупность функций ,т.е сумму прямой и обратной волн.u(t,x)=uп(t-  )+u0(t+
)+u0(t+  )
)
Если в точке линии с координатой х0 наведен импульс напряжения u(t0,x0), то значение напряжения u(tк,x0) будет иметь место во всех точках линии при х 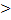 х0 с запаздыванием во времени.
х0 с запаздыванием во времени.
tP= 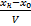 , т.е равным времени распространения.Распределение напряжения вдоль линии можно получить заменой аргумента t
, т.е равным времени распространения.Распределение напряжения вдоль линии можно получить заменой аргумента t 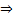 t-
t-  - для прямой волны(х
- для прямой волны(х 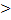 х0), t
х0), t 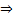 t+
t+  - для обратной волны(х
- для обратной волны(х 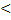 х0).Оба импульса распределяются вдоль линии без изменения формы со скоростью V в противоположных направлениях.
х0).Оба импульса распределяются вдоль линии без изменения формы со скоростью V в противоположных направлениях.
Распространение импульса напряжения вдоль линии приводит к возникновению тока (изменение заряда на проводниках).
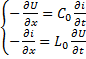 , i=
, i= 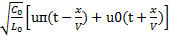 iп(x,t)=
iп(x,t)= 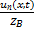 ,ZB=
,ZB= 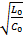 - волновое сопротивление линии
- волновое сопротивление линии
i(x,t)=iп 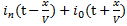
Аналитическое решение телеграфных уравнений можно получить операторным методом.
Рассмотрим процессы в линии при нулевых начальных условиях U=U(x,o), i(x,o)=0.Если в линии в начальный момент времени имеется заряд и напряжение, то можно воспользоваться принципом наложения с рассмотреть 2 режима:
а)переходный процесс в заряженной линии б)установившийся режим в линии без воздействия.
Телеграфные уравнения в операторном виде 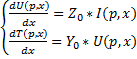
U(p,x) и I(p,x)- изображения по масштабу функций времени для каждой координаты х-линии:
Z0=r0+pL0, Y0=g0+pC0
Операторные погонные параметры линии,продольное сопротивление и поперечная проводимость.
Систему уравнений сведем к одному из уравнений: 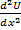 = γ2(p)U(x,p) ,
= γ2(p)U(x,p) , 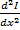 = γ2(p)I(x,p)
= γ2(p)I(x,p)
γ= 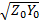 =
= 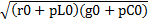 - постоянное распространение. Решение уравнений имеет вид:
- постоянное распространение. Решение уравнений имеет вид:
U(x,p)=А1е-γх+ А2еγх I(x,p)= 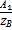 е-γх -
е-γх - 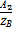 еγх, А1 и А2 –постоянные,зависящие от граничных условий.ZB=
еγх, А1 и А2 –постоянные,зависящие от граничных условий.ZB= 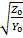 =
= 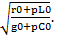 По аналогии с процессами в линиях без потерь решение можно записать в виде
По аналогии с процессами в линиях без потерь решение можно записать в виде
U(x,p)=Uп+U0, I(x,p)=Iп-I0 Uп,U0, Iп,I0 –изображение прямых и обратных волн U и I соответственно
Следует иметь ввиду, что название прямой и обратной волн для изображения условны,т.к. реальные процессы в некоторых видах линий не имеют характера распространяющейся волны.
Вид решения для изображений зависит от 2-х операторных величин: вторичных параметров γ(р) и ZB(p) ,определяющих особенности процессов в различных линиях.
Для линии без потерь γ=p* 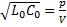 , ZB=
, ZB= 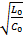 , причем волновое сопротивление имеет резистивный характер.
, причем волновое сопротивление имеет резистивный характер.
Если в линии без потерь существует только прямая волна,то U(x,p)= U(0,p)*е-γх, I(x,p)= U(0,p)*е-γх / ZB
Переход от изображений к функциям времени согласно теореме запаздывания дает
u(t,x)=u(0,t-  ) i(t,x)=u(0,t-
) i(t,x)=u(0,t-  )/ ZB
)/ ZB
Резистивно-емкостная линия характеризуется системой уравнений: 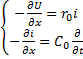 ,которая сводится к уравнению для напряжения
,которая сводится к уравнению для напряжения 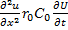 .
.
Полученное уравнение не является волновым и его решение не может быть представлено совокупностью волн. В операторном виде: U(x,p)=А1 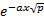 + А2
+ А2 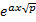 .γ=
.γ= 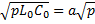 -постоянное распространение
-постоянное распространение
5.Установившиеся режимы в линиях.
При действии на входе линейной цепи с распределенными параметрами установившегося синусоидального сигнала U и I в любой точке линии так же будут синусоидальными, одной частоты с отличающимися амплитудами и начальными фазами.
Задача расчета процессов линии сводится к нахождению распределения амплитуд и фаз синусоидальных U и I в зависимости от координаты.
В символической форме записи телеграфные уравнения сводятся к системе обыкновенных дифференциальных уравнений.
- 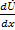 = (r0+ jωL0)İ=
= (r0+ jωL0)İ= 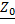 İ -
İ - 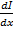 = (g0+ jωC0)
= (g0+ jωC0) 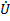 =
= 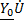
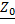 ,
, 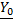 - полные погонные сопротивления и проводимость
- полные погонные сопротивления и проводимость
Решение уравнений: 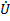 (x)=
(x)= 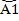 е-γх+
е-γх+ 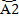 еγх
еγх 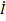 (x)=
(x)= 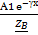 –
– 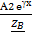 , где γ=
, где γ= 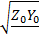 - комплексная постоянная распределения на частоте ω,
- комплексная постоянная распределения на частоте ω, 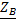 =
= 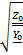 - комплексное волновое сопротивление на частоте ω
- комплексное волновое сопротивление на частоте ω
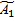 ,
, 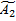 - комплексные коэффициенты,зависящие от граничных условий.
- комплексные коэффициенты,зависящие от граничных условий.
Комплексы прямой и обратной волн: 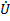 (x) =
(x) = 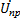 (х)+
(х)+ 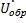 (х)
(х) 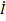 (x) =
(x) = 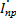 (х)+
(х)+ 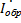 (х)
(х)
Волновое сопротивление и постоянная распространения определяет характер процессов в линии при синусоидальном воздействии и носит название вторичных параметров. Первичные параметры линии : r0, g0, c0, l0… Постоянная распространения включает в себя коэффициенты затухания α и коэффициент фазы β.
γ= 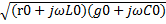 = α+β
= α+β
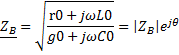
Вторичные параметры завися от типа линии передачи и использованной частоты.Вторичные параметры линии постоянного тока: γ= 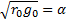
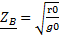
Для линии без потерь r0=0, g0= 0: γ= 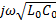 α=0 β=
α=0 β= 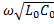 ,
, 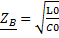
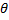 =
= 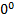
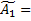 A1*
A1* 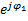
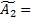 A2*
A2* 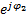 , u(x,t)=A1
, u(x,t)=A1 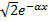
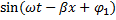 + A2
+ A2 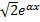
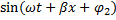
i(x,t)= 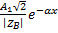
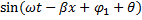 -
- 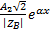
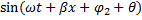
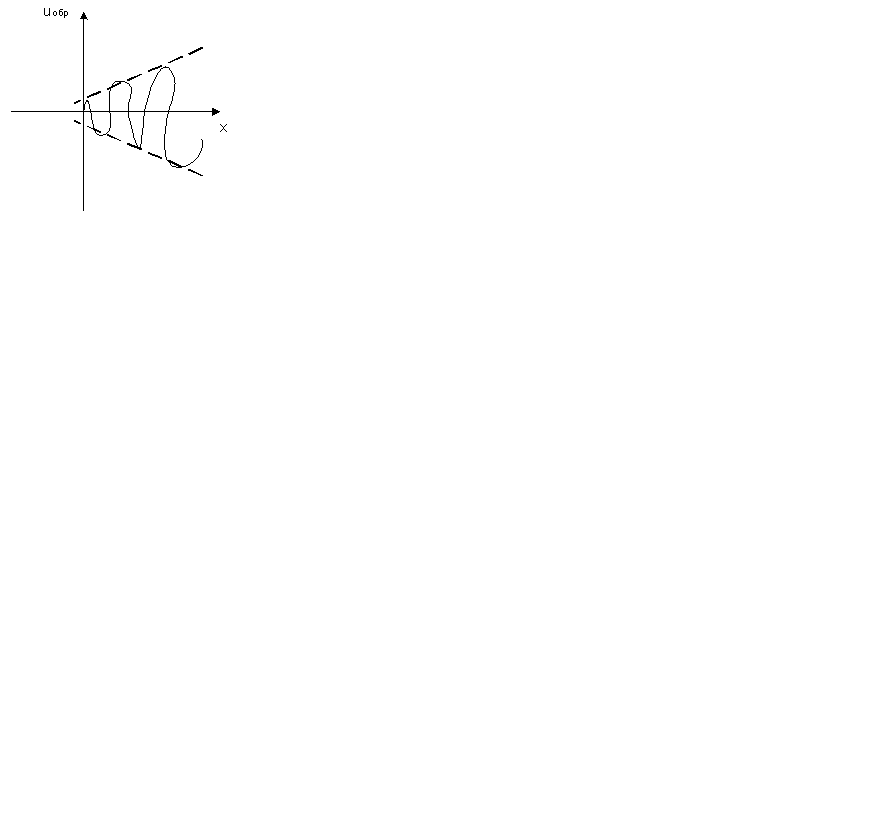 Фиксированные точки линии Хн напряжения представляют собой синусоидальную функцию времени.
Фиксированные точки линии Хн напряжения представляют собой синусоидальную функцию времени.
u(xн,t)=A 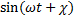
 Если рассмотреть напряжение вдоль линии в фиксированный момент времени t1 ,то оно представляет собой сумму затухающих синусоидальных функций.Одну называют прямой волной напряжения,вторую-обратной волной напряжения.
Если рассмотреть напряжение вдоль линии в фиксированный момент времени t1 ,то оно представляет собой сумму затухающих синусоидальных функций.Одну называют прямой волной напряжения,вторую-обратной волной напряжения.
 Для линии без потерь при α=0 и момента времени t2 амплитуда синусоиды не изменяется.а начальная фаза увеличивается на ω∆t. Кривая как бы передвинулась на значение ∆х = ω∆t/β.
Для линии без потерь при α=0 и момента времени t2 амплитуда синусоиды не изменяется.а начальная фаза увеличивается на ω∆t. Кривая как бы передвинулась на значение ∆х = ω∆t/β.
Синусоидальное распределение напряжения (тока) в пространстве по координате х называют бегущей волной. Основные характеристики бегущей волны: фазовая скорость и длина волны.Фазовая скорость-скорость перемещения точки с неизвестным фазовым углом. Vф= 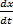 =
= 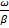
Длина волны λ – расстояние,на которое распространяется бегущая волна за период Т: λ= Vф*Т
Для обратной волны фазовая скорость отрицательна.С энергетической точки зрения важно распределение вдоль линии действительных значений напряжения и тока при известной нагрузке.
Для начала линии х=0 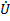 (x)=
(x)= 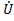 chγx -
chγx - 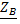 I1 sinγx
I1 sinγx 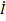 (x)=-
(x)=- 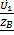 shγx +
shγx + 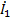 chγx
chγx
Относительно конца линий: 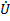 (y)=
(y)= 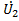 chγy +
chγy + 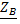 shγy
shγy 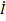 (x)=-
(x)=- 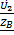 shγy +
shγy + 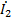 chγy. Для линии без потерь γ= jβ
chγy. Для линии без потерь γ= jβ
Введем комплексное сопротивление нагрузки 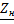 =
= 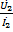 .
.
Входное сопротивление линии в произвольной точке. 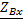 (y)=
(y)= 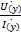
Сопротивление полученных выражений с общим решением для линий без потерь приврдит к выводу,что реализован режим бегущей волны.
Действующие значения выражений напряжения и тока не изменяются вдоль линии.Такой режим работы называют режимом согласования нагрузки с волновым сопротивлением линии.
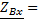 RΩ=
RΩ= 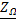 - для любой точки линии
- для любой точки линии
Для режима разомкнутой линии 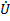 (y)=
(y)= 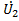 cosβy
cosβy 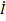 (y)=-
(y)=- 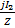 sinβy
sinβy
Распределение модулей действующих значений I(y)=- 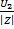 sinβy
sinβy
Такое распределение действующих значений вдоль линии называется режимом стоячих волн.
u(y,t)=U2msinωtcosβy i(y,t)=I2mcosωtsinβy
В фиксируемой точке линии получаем синусоидальные U и I ,имеющие фазовый сдвиг П/2.Если в различные моменты времени зафиксировать картины распределения U и I вдоль линии,то получим синусоидальные кривые,у которых нулевые точки неподвижны,а изменяется синусоида.
В режиме размыкания выхода активная мощность =0 в любой точке линии.Входное сопротивление линии имеет реактивный характер.
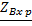 =-jZBctgβy
=-jZBctgβy
 С энергетической точки зрения оптимальным является режим согласованной нагрузки, поскольку в других режимах имеются отрезки линии с повышенным напряжением и отрезки с большим значением тока. Повышение напряжения затрат на улучшение изоляции для снижения сопротивления утечки и предотвращения пробоя. Большое значение тока приводит к необходимости увеличения сечения проводников добавочному расходу металла. В реальных линиях предпринимаются меры по приближению режима работы линии к согласованному с использованием различных согласующих устройств.
С энергетической точки зрения оптимальным является режим согласованной нагрузки, поскольку в других режимах имеются отрезки линии с повышенным напряжением и отрезки с большим значением тока. Повышение напряжения затрат на улучшение изоляции для снижения сопротивления утечки и предотвращения пробоя. Большое значение тока приводит к необходимости увеличения сечения проводников добавочному расходу металла. В реальных линиях предпринимаются меры по приближению режима работы линии к согласованному с использованием различных согласующих устройств.








