II . Переходные процессы в электрических цепях.
1. 
 Основные понятия и принципы анализа переходных процессов.
Основные понятия и принципы анализа переходных процессов.

Такие токи устанавливаются лишь через некоторое время после вкл цепи или после изменения параметров. Могут существовать все время пока к ней приложено напряжение, и параметры остаются неизменными. 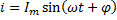
Эти токи называются установившимися токами, а соответственно напряжение на отдельных участках установившимися напряжениями.
К каждому установившемуся режиму электрической цепи соответствует строго определенные энергетические состояния

рассеивает
накапливает напряжение
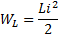
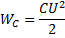
Любое изменение состояния электрической цепи (вкл, отк, изменение параметров и т. д.) называют коммутацией.
Будем считать, что процесс коммутации осуществляется мгновенно. Энергетическое состояние не может изменяться мгновенно.

 Если предположить, что ток в цепи изменяется мгновенно от
Если предположить, что ток в цепи изменяется мгновенно от 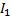 к
к 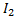 , то это будет означать, что в индуктивности в этот момент времени индуцируется ЭДС самоиндукции
, то это будет означать, что в индуктивности в этот момент времени индуцируется ЭДС самоиндукции
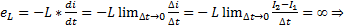 ток не может изменяться скачкообразно.
ток не может изменяться скачкообразно.
Любая ЭДС самоиндукция препятствует изменению тока цепи, поэтому предположение о мгновенном изменении токов цепи не верно!
Законы коммутации:
· Ток в цепи с индуктивностью не может изменяться скачком;
· Напряжение на зажимах конденсатора или другого емкостного элемента не может измениться скачком.
Индуктивные и емкостные элементы являются инерционными. Вследствие чего, для изменения энергет. состояния электрической цепи требуется некоторый промежуток времени в течении которого происходит переходный процесс. Длительность переходного процесса зависит от параметров цепи.
Как и любой динамический процесс, переходный процесс в электрических цепях описывают дифференциальными уравнениями. Режим линейных электрических цепей с постоянными параметрами R, L, C описываются линейными дифференциальными уравнениями с постоянными коэффициентами.
Пример:

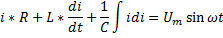
Полное решение неоднородного дифференциального линейного уравнения находится в виде:
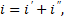
где 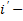 частное решение неоднородного дифференциального уравнения;
частное решение неоднородного дифференциального уравнения;
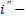 общее решение неоднородного дифференциального уравнения.
общее решение неоднородного дифференциального уравнения.
Ток 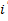 поддерживается в цепи напряжением источника питания и является установившемся током (принужденное составляющее). Ток
поддерживается в цепи напряжением источника питания и является установившемся током (принужденное составляющее). Ток 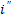 называется свободным током (свободное составляющее), т. к. его определяют в свободном режиме цепи.
называется свободным током (свободное составляющее), т. к. его определяют в свободном режиме цепи.
6. Переходные процессы в rLC цепи(последовательном контуре).
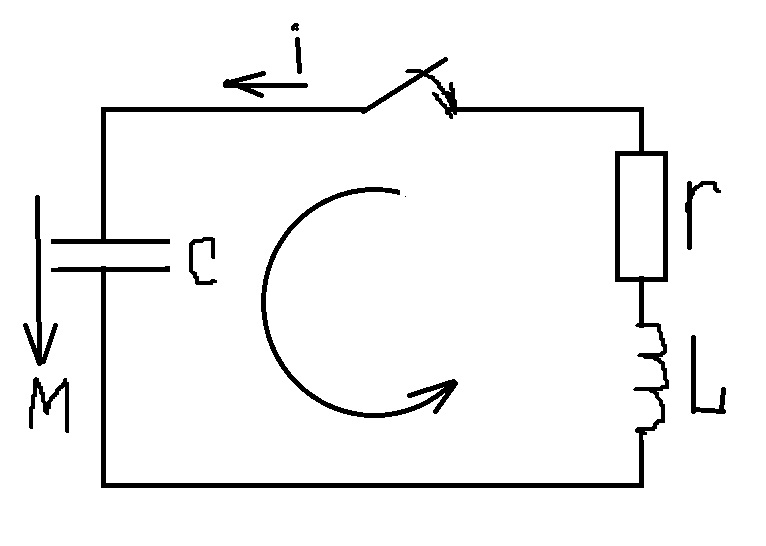
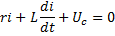
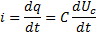
Подставляя значение тока в исходное уравнение после дифференцирования получаем для Uс дифференциальное уравнение 2-го порядка:
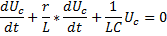
Заряд на конденсаторе удовлетворяет такому же диф. уравнению:
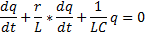
Дифференцируя это уравнение по времени, получаем аналогичное уравнение для тока:
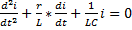 ,
, 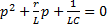 ,
, 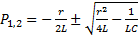
Характер свободного процесса зависит только от параметров rLC цепи, т.е. от вида корней харктерестического уравнения.
Характер свободного процесса зависит от знака подкоренного выражения.
2. Переходные процессы в цепи с последовательным соединением элементов с R и L при подключении ее к источнику постоянного напряжения.
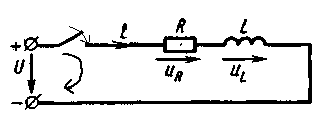 В начальный момент времени тока в цепи нет и энергия магнитного поля катушки равна 0:
В начальный момент времени тока в цепи нет и энергия магнитного поля катушки равна 0: 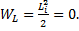
После подключения к источнику постоянного напряжения в установившемся режиме существует ток 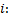
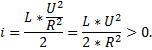
Следовательно, в то время когда происходит изменение энергии магнитного поля катушки, в цепи имеет место переходной процесс и существует переменный ток 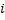 как некоторая функция времени
как некоторая функция времени
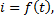
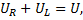
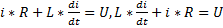 ,
, 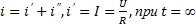
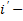 частное решение;
частное решение; 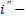 общее решение.
общее решение. 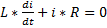
Решаем однородное дифференциальное уравнение 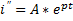 ,
, 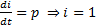 ,
, 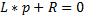
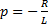 ,
, 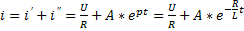
Постоянную интегрирования 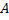 определяем с учетом первого закона коммутации.
определяем с учетом первого закона коммутации. 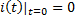
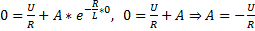 ,
, 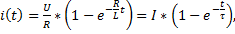
 где
где 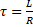 имеет размерность времени. Ее называют постоянной времени цепи. Характеризует скорость протекания переменного процесса. Чем больше
имеет размерность времени. Ее называют постоянной времени цепи. Характеризует скорость протекания переменного процесса. Чем больше 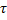 , тем дольше существует ток
, тем дольше существует ток 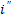 и тем длительнее переходный процесс.
и тем длительнее переходный процесс.
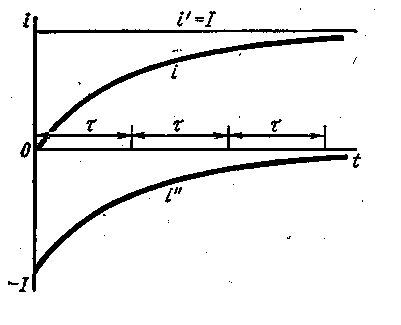
Свободный ток 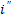 в момент времени t=0 равен по значению установившемуся току I, но противоположен по направлению. С течением времени этот ток уменьшается до 0. Общий ток цепи изменяется по экспоненциальному закону. При
в момент времени t=0 равен по значению установившемуся току I, но противоположен по направлению. С течением времени этот ток уменьшается до 0. Общий ток цепи изменяется по экспоненциальному закону. При 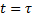
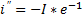 .
.
Постоянная времени равна такому промежутку времени, в течении которого свободный ток уменьшается в 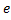 раз.
раз.
Как правило, уже при 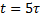 ток в цепи отличается от установившегося тока менее чем на 1%, поэтому его можно считать установившемся.
ток в цепи отличается от установившегося тока менее чем на 1%, поэтому его можно считать установившемся.
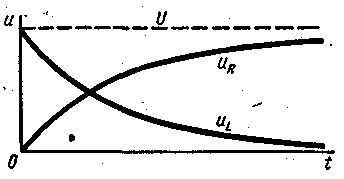 Падение напряжения на резисторе изменяется по такому же закону что и ток
Падение напряжения на резисторе изменяется по такому же закону что и ток
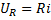
Падение напряжения на индуктивной катушке:
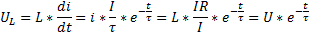
Напряжение убывает с течением времени от значения напряжения источника питания до 0.
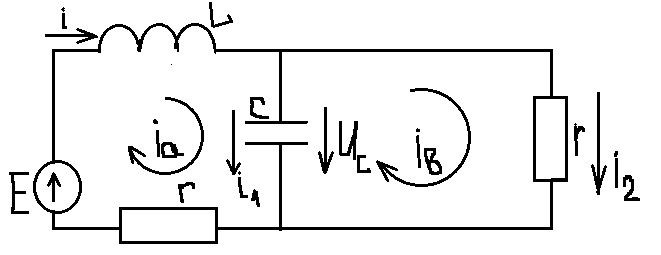 7. Общий случай расчета переходных процессов классическим методом.
7. Общий случай расчета переходных процессов классическим методом.
1) Для цепи после коммутации составляют систему ДУ по 1 и 2 закону Кирхгоффа: 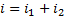
1 контур: 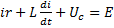
2 контур: 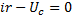
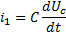
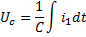
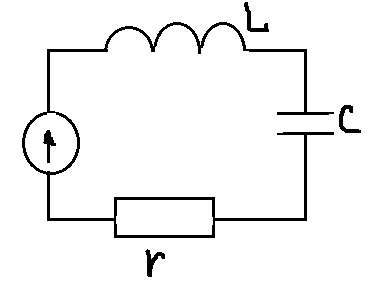 После подстановки Uc в исходную систему уравнений, и диф-ии, получим ситему уравнений для трех неизвестных токов:
После подстановки Uc в исходную систему уравнений, и диф-ии, получим ситему уравнений для трех неизвестных токов:
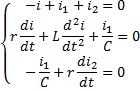
2) Независимые начальные условия: ток на индуктивном элементе iL(0+) после коммутации и Uc(0+) неизвестны. Они определяются из расчета режима цепи до коммутации с применением закона коммутации:
1 закон: iL(0-)=iL(0+) 2 закон: Uс(0-)=Uc(0+)
Uc(0-)=E iL(0-)=I’=0 Начальные условия будут: Uc(0+)=E и iL(0+)=0
3)Запишем искомую величину в виде двух составляющих: своб-я и принуждения: 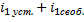
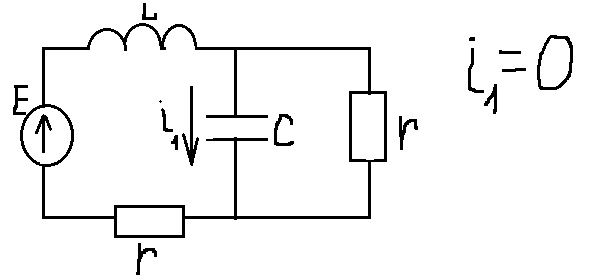 4) Установившемуся состоянию найдем, рассчитав режим цепи, постоянную тока после коммутации:
4) Установившемуся состоянию найдем, рассчитав режим цепи, постоянную тока после коммутации:
5) Составим характерестичесое уравнение и найдем его корни. Они могут быть действительные, разные, равные или комплексные сопряженные.
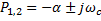
6) Запишем свободную составляющую и пост. интегрирования, обращая внимание на вид корней.
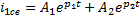 ,
, 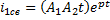
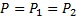 ,
, 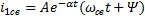
7) Искомое решение с двумя пост. Интегрирования: 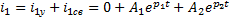
8) Для определения двух постоянных интегрирования запишем полученные решения:
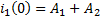 ,
, 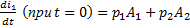
Начальное значение тока определим из системы дифференциальных уравнений:
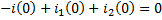 ,
, 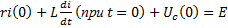 ,
, 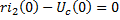
В этой системе уравнений величины i(0) и Uc(0) были найдены. Следовательно остальные три величины i1(0), i2(0) и di/dt (при t=0) можно определить.
9) После определения постоянных А1 и А2, остается подставить их в искомое решение. Для определения других токов и напряжений не требуется заново выполнять все этапы расчета.
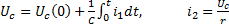 ,
, 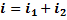
8. Основные положения операторного метода расчета переходных процессов в электрических цепях.
Операторный метод - основан на использовании понятия об изображении функции времени.
В этом методе каждой функции времени соответствует функция новой переменной (Р), и наоборот функции Р отвечает определенная функция времени.
Основан на преобразовании Лапласса: 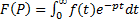
Операторный метод позволяет свести операцию дифференцирования к умножению, операцию интегрирования к делению, что облегчает интегрирование дифференциальных уравнений.
9. Изображение напряжения на индуктивности.
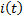 ,
, 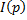 ,
, 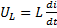 ,
, 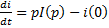 ,
, 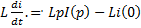
При i(0)=0: 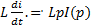
10. Изображение напряжения на конденсаторе. 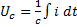 ,
, 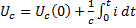
К моменту времени t напряжение на конденсаторе определяется не только током, протекавшим через конденсатор, в интервале времени от 0 до t, но и тем напряжением которое на нем было при t=0.
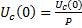 ,
, 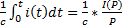 ,
, 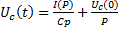
11. Закон Ома в операторной форме. Внутренние ЭДС.
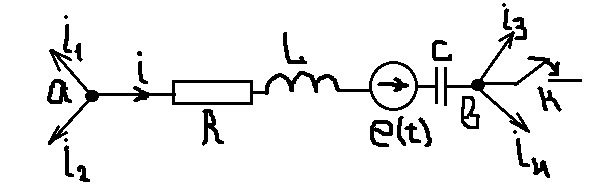
Замыкание ключа приводит к переходному процессу. До коммутации ток:
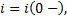
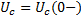
Выразим потенциал точки а через потенциал точки b для послеком-мутационного режима:
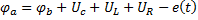 ,
, 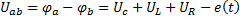 ,
,
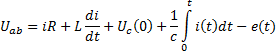
К последнему выражению применим преобразование Лапласса:
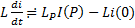 ,
, 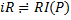 ,
, 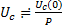 ,
, 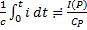 ,
, 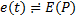
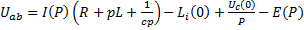 ,
, 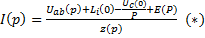 ,
,
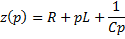
z(p) представляет собой операторное сопротивление участка цепи между точками а и b.
L*i(0) – представляет собой внутренний ЭДС, обусловленный запасом энергии в магнитном поле индуктивности вследствие протекания через нее тока i(0) непосредственно до коммутации. Запасена энергия: 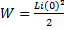
Uc(p)/P – внутренняя ЭДС, обусловленная запасом энергии в электрическом поле конденсатора, в следствие наличия напряжения на нем Uc(0) непосредственно до коммутации
Уравнение (*) – закон Ома в операторной форе для участка цепи, содержащее ЭДС, при ненулевых начальных условиях.
Операторная схема замещения:
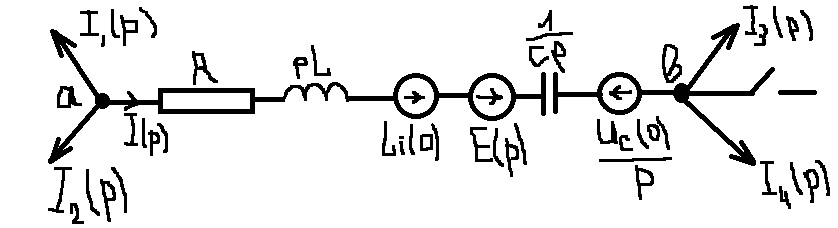 В частном случае, когда на участке отсутствует ЭДС и к моменту коммутации ток на индуктивности равен 0, и напряжение а конденсаторе до коммутации Uc(0-)=0, закон Ома запишется в виде:
В частном случае, когда на участке отсутствует ЭДС и к моменту коммутации ток на индуктивности равен 0, и напряжение а конденсаторе до коммутации Uc(0-)=0, закон Ома запишется в виде: 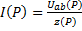 - закон Ома в операторной форме для участка цепи, не содержащего ЭДС, и при нулевых начальных условиях.
- закон Ома в операторной форме для участка цепи, не содержащего ЭДС, и при нулевых начальных условиях.
12. Первый закон Кирхгофа в операторной форме
Алгебраическая сумма операторных токов в узле равна нулю. 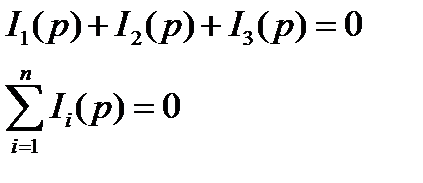
13. Второй закон Кирхгофа в операторной форме
Для любого замкнутого контура любой электрической цепи можно составить уравнение по второму закону Кирхгофа для мгновенных значений. Предварительно необходимо выбрать положительные направления для токов в ветвях и направление обхода контура.
 Запишем уравнение по второму закону Кирхгофа для контура рис. 8.28. Контур обходим по часовой стрелке. Учтем, что индуктивности
Запишем уравнение по второму закону Кирхгофа для контура рис. 8.28. Контур обходим по часовой стрелке. Учтем, что индуктивности 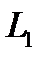 и
и 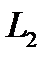 связаны магнитно. При выбранных положительных направлениях для токов
связаны магнитно. При выбранных положительных направлениях для токов 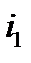 и
и 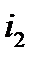 между
между 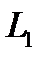 и
и 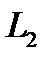 имеет место согласное включение.
имеет место согласное включение.
Падение напряжения на 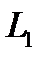 равно
равно 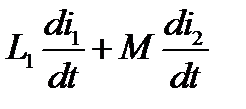 ;— на
;— на 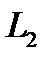 составляет
составляет 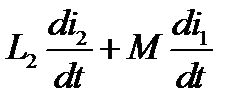 . При составлении уравнения учтем, что начальное напряжение на конденсаторе равно
. При составлении уравнения учтем, что начальное напряжение на конденсаторе равно 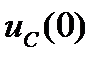 . Пусть оно действует согласно с током
. Пусть оно действует согласно с током 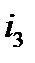 . Начальное значение
. Начальное значение 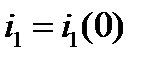 тока
тока 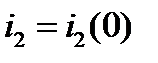 Имеем
Имеем
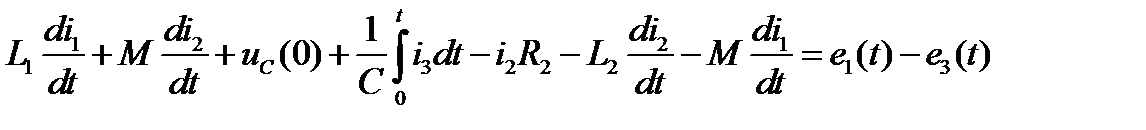 (8.44)
(8.44)
Каждое из слагаемых (8.44) заменим операторным изображением:
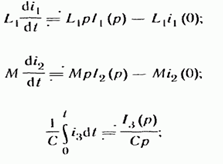
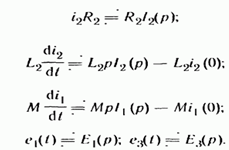 (8.45)
(8.45)
Подставив (8.45) в (8.44), объединим слагаемые с 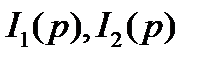 и
и 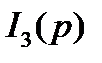 перенесем в правую часть
перенесем в правую часть 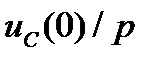 ,
, 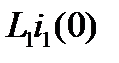 и другие внутренние ЭДС. В результате получим
и другие внутренние ЭДС. В результате получим
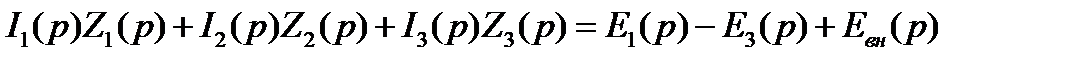 (8.46)
(8.46)
где 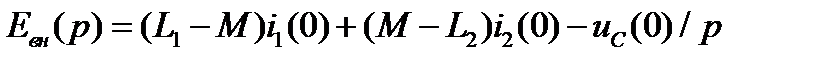
В более общем виде у-ие (8.46) можно записать так: 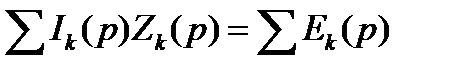 (8.47)
(8.47)
Уравнение (8.47) представляет собой математическуюзапись второго закона Кирхгофа в операторной форме. В состав 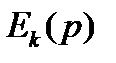 в общем случае входят и внутренние ЭДС.
в общем случае входят и внутренние ЭДС.
12. Первый закон Кирхгофа в операторной форме.
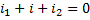
Применив преобразование Лапласса и воспользовавшись тем, что сумма изображений равна изображению сумм, получим, что сумма операторных токов в узле равна 0:
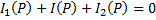
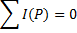
14. Расчет переходных процессов операторным методом в RC контуре при ступенчатом воздействии.

Схема замещения цепи для L-изображений (L- преобразование Лапласа ):
L- изображение токов в контуре
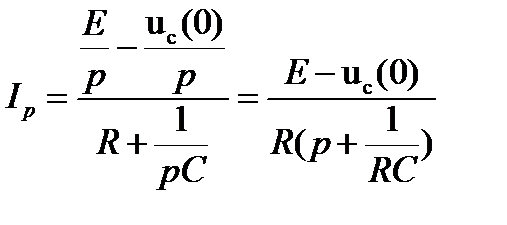
Найденному изображению согласно таблице соответствий находится оригинал. 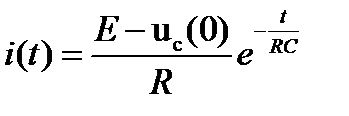
Он определяет закон изменения токов в контуре.
При нахождении L-изображения напряжения на ёмкости следует иметь в виду что оно равно сумме L-изображений напряжения на не заряженной емкости и начального условия.
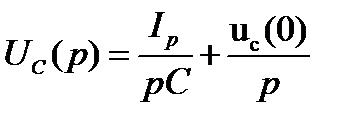
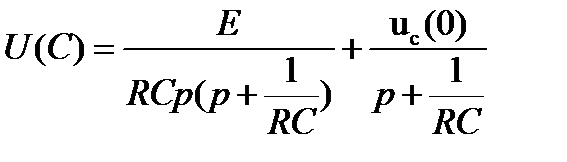
Используя таблицу соответствия и учитывая линейность обратного преобразования Лапласа находим напряжение на конденсаторе как функция времени.
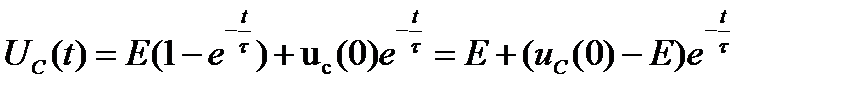
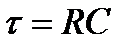
13. Второй закон Кирхгофа в операторной форме.

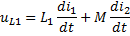
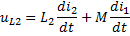
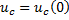
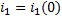
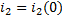
По второму закону Кирхгофа:
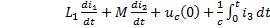 -
- 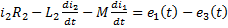 .
.
Каждое из слагаемых заменяем операторным выражением:
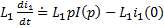 ,
, 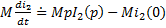 ,
, 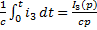 ,
, 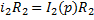
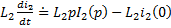 ,
, 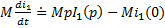 ,
, 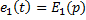 ,
, 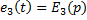
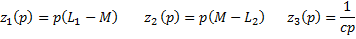
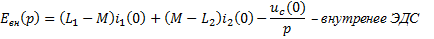
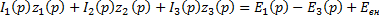
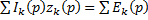 второй закон Кирхгофа.
второй закон Кирхгофа.
В сумму 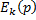 в общем случае входят и внутреннее ЭДС.
в общем случае входят и внутреннее ЭДС.
15. Расчет переходных процессов операторным методом в параллельном колебательном контуре при ступенчатом воздействии.
Пусть к параллельному колебательному контуру подсоеденены ступенчатые воздействия тока при нулевых начальных условиях

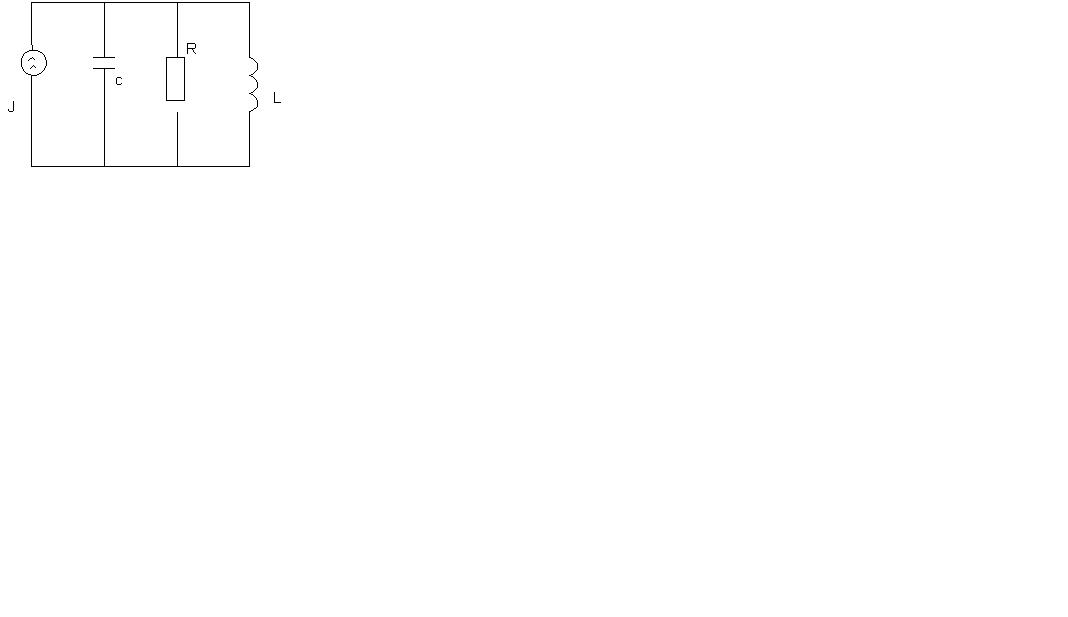 Нарисуем:
Нарисуем:
L-изображение воздействия: 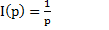 Операторное:
Операторное: 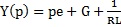
L-изображение напряжения на зажимах 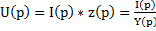
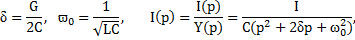
Используя таблицы соответствия находим оригинал:
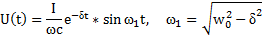
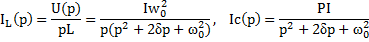
По таблице соответствия находим оригинал токов:
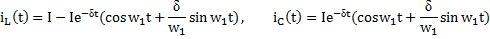
Найденные решения соответствуют случаю комплексно-сопряженных полей полинома: 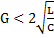
Если воздействие к тому же контуру подведено при ненулевых начальных условиях, то целесообразно использовать схемы замещения реактивных элементов для ненулевых начальных условий, т.е. схемы замещения с источника тока, тогда L-изображения воздействия на контур:
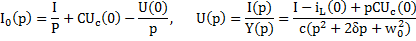
Для нахождения соответствующего оригинала с помощью таблиц следует представить это изображение в виде суммы:
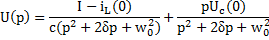
Если 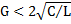 , в результате простого преобразования находим выражение для напряжения на контуре в режиме переходных колебаний:
, в результате простого преобразования находим выражение для напряжения на контуре в режиме переходных колебаний:
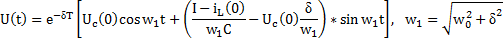
Аналогично могут быть найдены токи в элементах контура.
16. Расчет переходных процессов операторным методом в параллельном колебательном контуре при гармоническом воздействии
Контуру при нулевых начальных условиях подведено гармоническое воздействие t=0.
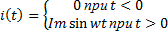
Пусть частота воздействия совпадает с резонансной частотой контура.
L-изображение воздействия:
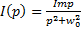 ,
, 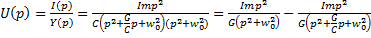
Последнее выражение находится, если воспользоваться методом неопределенных коэффициентов. Изображению U соответствует оригинал:
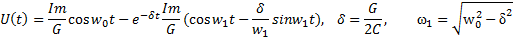
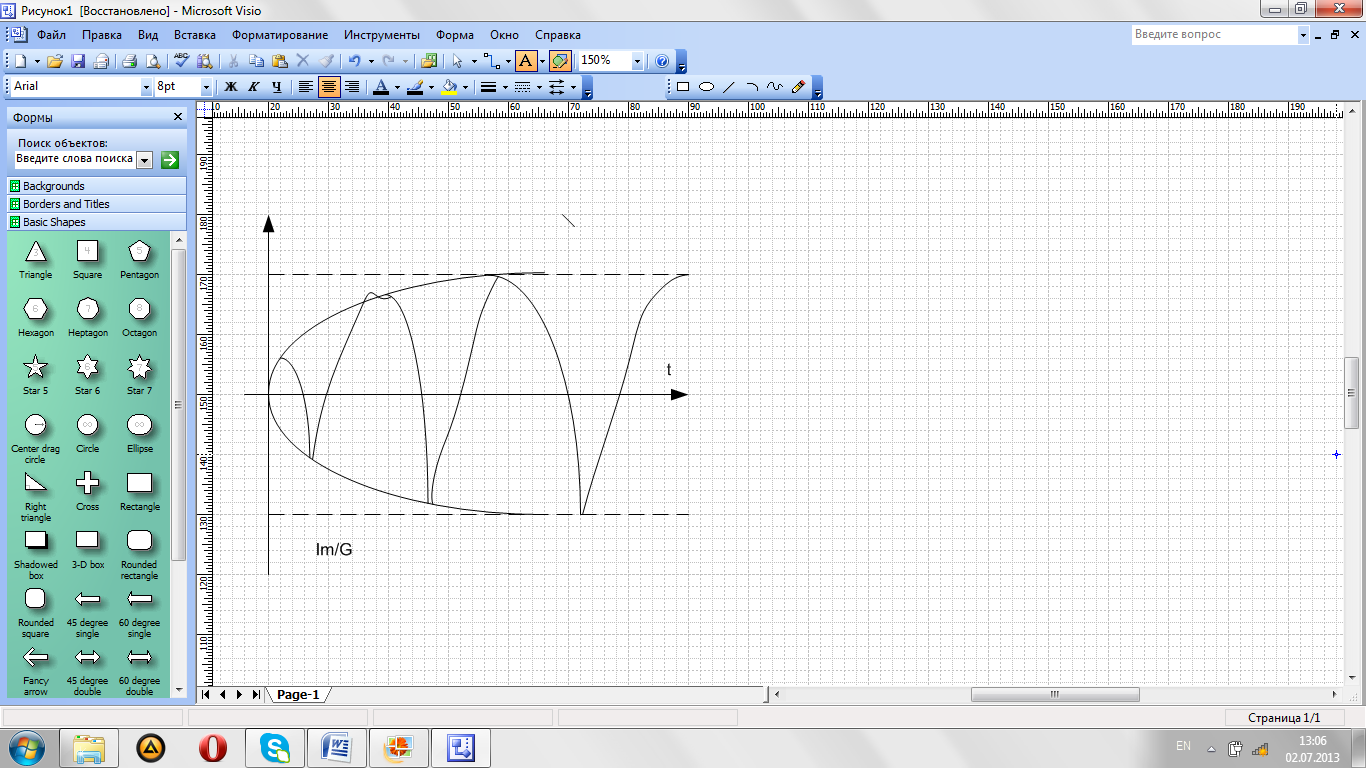 При типовых значениях добротности контура
При типовых значениях добротности контура
Q>>1 w1≈w0 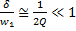
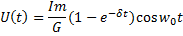
Функция, описывающая колебания, отличается от гармонической тем, что ее амплитуда монотонно возрастает, стремясь к установившемуся значению. Закон, по которому возрастает амплитуда колебания описывается огибающей колебания частотно заполняющего период: 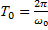 .
.
Принципиально важным является то, что время установления колебания тем больше, чем ярче выражено в контуре явление резонанса.
17. Последовательность расчета ПП операторным методом
1. Из докумматационной схемы определяются токи через катушки индуктивности,и индуктивности и напряжения на конденсаторе (независимые начальные условия)
2. Составляется операторная схема замещения
3. Рассчитывается операторная схема и определяются искомые величины
4. По изображениям находят оригинал искомой величины, используя либо форменные выражения, либо таблицы соответсвия.
18. Расчет переходных процессов методом переменных состояния.
Метод переменных состояния основан на составлении и решении ур-ий состояния - диф.ур. первого порядка, разрешенных отн-но производных. Известно, что расчет ПП сводится к интегрированию диф-го ур-я перв. порядка:
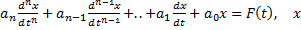 - напряжение, ток, заряд.
- напряжение, ток, заряд.
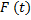 - функция, зависящая от параметров источников энергии.
- функция, зависящая от параметров источников энергии.
Это уравнение сводят к системе 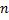 диф.ур. первого порядка путем введения переменных состояния:
диф.ур. первого порядка путем введения переменных состояния:
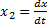 ,
, 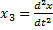 ,
, 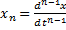 .
.
Таким образом, переменными состояния могут быть сама исходная величина и ее производная.
Из уравнений переменных состояния получают систему диф.ур.перв.порядка:
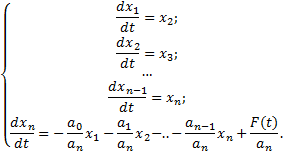
Система ур-ий эквивалентна одному уравнению n-ого порядка.
19. Последовательность расчета переходных процессов методом переменных состояния.
1. Выбирают переменные состояния. Токи в инд.катушках и напряжения на емкостных элементах.
2. Из докоммутационной схемы определяют токи через катушки индуктивности и напряжения на конденсаторах и составляют матрицу начальных значений независимых переменных.
3. Для послекоммутационного режима составляют систему диф.ур.перв.порядка и разрешают ее относительно производных. Через переменные 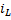 ,
, 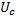 и параметров источников ЭДС и источников тока. Уравнения состояния получают либо с применением законов Кирхгофа, либо с применением метода наложения, либо с помощью топологических соотношений.
и параметров источников ЭДС и источников тока. Уравнения состояния получают либо с применением законов Кирхгофа, либо с применением метода наложения, либо с помощью топологических соотношений.
4. Составляют уравнения для выходных переменных (искомых величин), в кот. искомые переменные выражают через переменные состояния и параметров источников энергии. Полученные уравнения удобнее записывать в матричной форме.
5. Решают уравнения состояния и находят закон изменения искомой величины функции времени.
20. Численный метод решения уравнений состояния динамической цепи.
Основой используемых численных методов является вычисление приращений переменных состояния Dxj за рассматриваемый промежуток времени — шаг интегрирования Dtk = tk+1 – tk = h
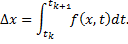
Методы численного интегрирования различаются по способу аппроксимации подынтегральной функции в последнем выражении. Наиболее простой вид имеют формулы
· явного метода Эйлера Dx = fk(xk, tk)h = fkh;
· неявного метода Эйлера Dx = fk+1h;
· метода трапеций Dx = (fk + fk+1)h/2.
Поскольку и последнее выражение содержит значения fk+1, не известные в начале вычислений на данном шаге, то метод трапеций также является неявным.
Реализация неявных методов требует на каждом шаге решения системы уравнений относительно неизвестных значений xk+1 в конце данного шага. Выбор шага интегрирования h связан с обеспечением точности и устойчивости численного решения. Обеспечение устойчивости является определяющим при интегрировании так называемых жестких систем дифференциальных уравнений, у которых корни характеристического уравнения резко различаются по модулю.








