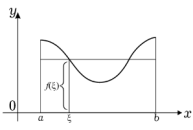
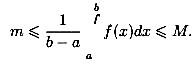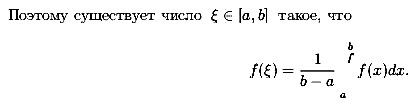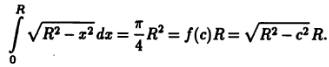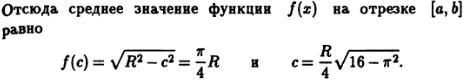Если , то используется обозначение и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.

Дата: 2025-05-01; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Если или , то обозначение сохраняется, а 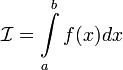называется расходящимся.

Пусть f(x) определена на (a,b], терпит бесконечный разрыв при x=b и 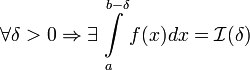. Тогда:

Если 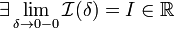, то используется обознач….

Если функция f(x) терпит разрыв во внутренней точке c отрезка , то несобственный интеграл второго рода определяется формулой:

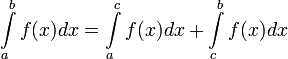
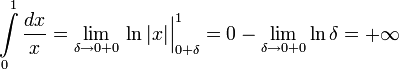
Свойства.

1) Если интеграл 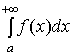сходиться, С – некоторое число, то интеграл 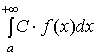также сходиться и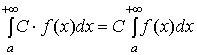

2) Если интегралы 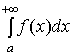и 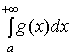сходятся, то интеграл 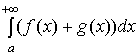только сходится и

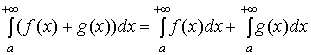
3) Если функци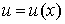и и 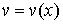интегрируемы при 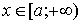, то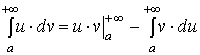

4) Пусть функция f(x) непрерывна при x>=a , функция 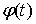определена, непрерывна и имеет непрерывную производную на промежутке 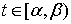конечном или бесконечном, где <

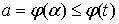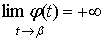
Тогда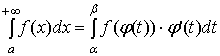

Билет 17

Д-во

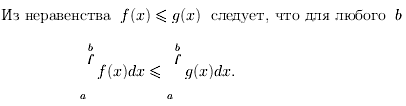
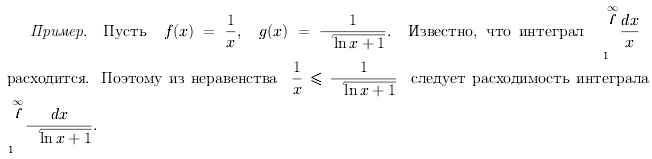
Билет 18

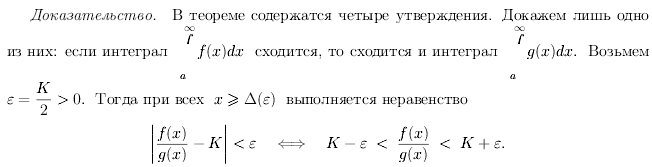
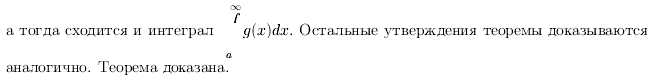
Пример.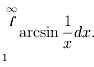

Обыкновенное дифференциальное уравнение 1-го порядка (n=1) имеет вид: 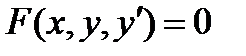или, если его удается разрешить относительно производной: 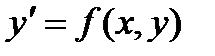. Общее решениеy = y ( x ,С) или общий интеграл 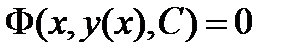уравнения 1-го порядка содержат одну произвольную постоянную. Единственное начальное условие для уравнения 1-го порядка 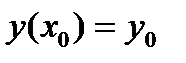позволяет определить значение константы из общего решения или из общего интеграла. Таким образом, будет найдено частное решение или, что тоже, будет решена задача Коши.

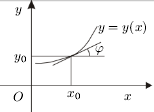
Геометрически общее решение уравнения 1-го порядка представляет собой семейство кривых на плоскости XOY, не имеющих общих точек и отличающихся друг от друга одним параметром – значением константы C. Эти кривые называются интегральными кривыми для данного уравнения. Интегральные кривые уравнения 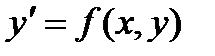обладают очевидным геометрическим свойством: в каждой точке 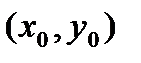тангенс угла наклона касательной к кривой равен значению правой части уравнения в этой точке: 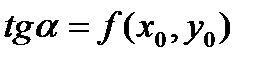. Другими словами, уравнение 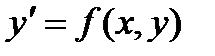задается в плоскости XOY поле направлений касательных к интегральным кривым.

Изоклиной ду называется множ-во точек пл-ти, в каждой из которых угловой коэф касательной к интегральным кривым этого ур-я имеет постоянное значение. Очевидно, ур-е изоклины имеет вид: f(x,y)=k, где к-значение углов коэфкачательной. Изоклины – линии уровня ф-цииf(x,y)

Пример. Найти общее решение уравнения y'+3y=e^2x и частное решение,удовлетворяющее начальным условиям х=0, у=1.
Решение. Данное уравнение является линейным..

Билет 19

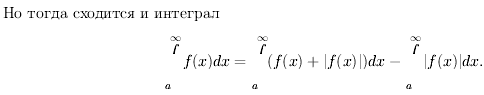
Рассмотрим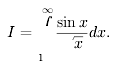

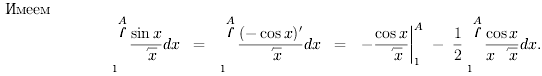
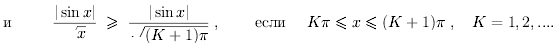
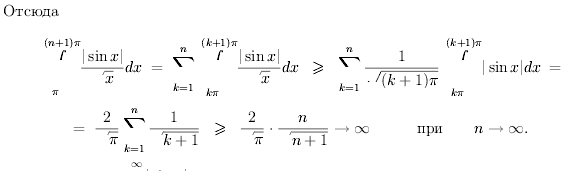
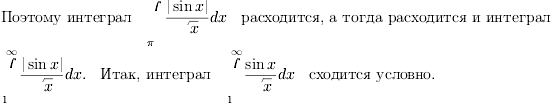
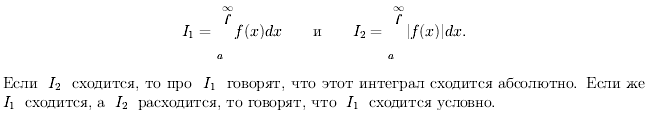
Билет 20

Несобственный интеграл I= 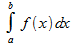называется: а)абсолютно сходящимся, если сходится интеграл 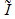= 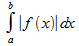, в этом случае говорят, что ф-ция f абс. интегрируема на промежутке [a;b); б)условно сходящимся, если интеграл I сходится, а 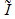расходится.

Свойства несобственных интегралов

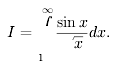
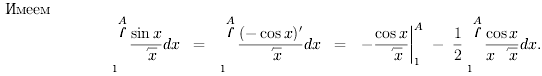
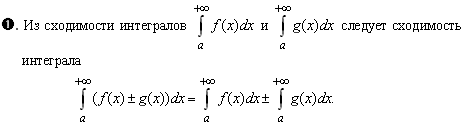
Общим решением дифференциального уравнения

F(x, y(x), y '(x), y ''(x), … , y^{(n )}(x)) = 0

называется функция

y = Ф(x, С₁, С₂, … , С_n),

содержащая некоторые постоянные (параметры) С₁, С₂, … , С_n, и обладающая следующими свойствами:

Ф(x, С₁, С₂, … , С_n) является решением уравнения при любых допустимых значениях С₁, С₂, … , С_m;

для любых начальных данных y(x₀) = y₀, y '(x₀) = y₁, y ''(x₀) = y₂, … , y^{(n − 1)}(x₀) = y_{n − 1}, для которых задача Коши имеет единственное решение,

существуют значения постоянных С₁ = A₁, С₂ = A₂, … , С_n = A_n, такие что решение y = Ф(x, A₁, A₂, …, A_n) удовлетворяет заданным начальным условиям.

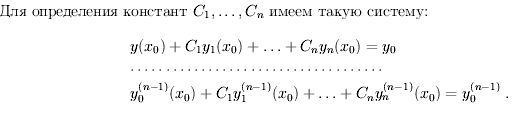
Билет 21

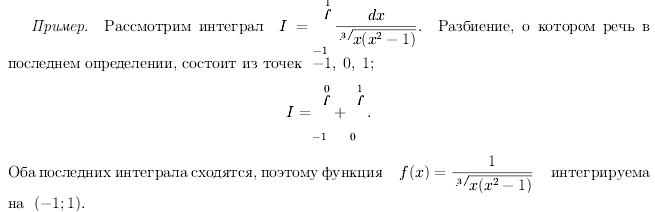
Билет 22

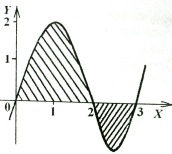
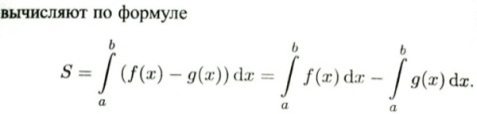
Билет 23

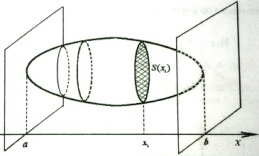
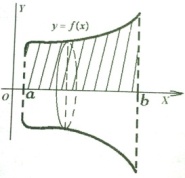
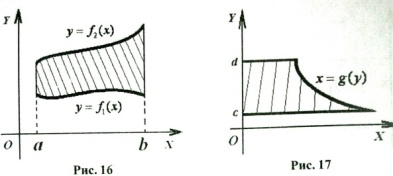
Билет 30

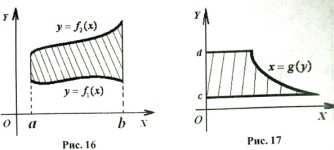
Общим решением дифференциального уравнения

F(x, y(x), y '(x), y ''(x), … , y^{(n )}(x)) = 0

называется функция

y = Ф(x, С₁, С₂, … , С_n),

содержащая некоторые постоянные (параметры) С₁, С₂, … , С_n, и обладающая следующими свойствами:

Ф(x, С₁, С₂, … , С_n) является решением уравнения при любых допустимых значениях С₁, С₂, … , С_m;

для любых начальных данных y(x₀) = y₀, y '(x₀) = y₁, y ''(x₀) = y₂, … , y^{(n − 1)}(x₀) = y_{n − 1}, для которых задача Коши имеет единственное решение,

существуют значения постоянных С₁ = A₁, С₂ = A₂, … , С_n = A_n, такие что решение y = Ф(x, A₁, A₂, …, A_n) удовлетворяет заданным начальным условиям.

теорема о структуре общего решения линейного однородного уравнения).

Если все коэффициенты уравнения линейного однородного дифференциального уравнениния непрерывны на отрезке [a;b] , а функции y₁(x), y₂(x),..., y_n(x) образуют фундаментальную систему решений этого уравнения, то общее решение уравнения имеет вид

y(x,C₁,..., C_n) = C₁y₁(x) + C₂y₂(x) + ... + C_ny_n(x),

где C₁,...,C_n — произвольные постоянные.

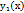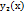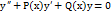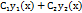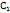Теорема. Если и – линейно независимые решения уравнения , то их линейная комбинация , где и 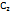– произвольные постоянные, будет общим решением этого уравнения.

Доказательство.

То, что 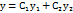есть решение уравнения (2.3), следует из теоремы о свойствах решений лоду 2-го порядка. Надо только еще показать, что решение 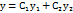будет общим, т.е. надо показать, что при любых начальных условиях 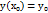, 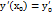можно выбрать произвольные постоянные 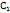и 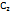так, чтобы удовлетворить этим условиям. Запишем начальные условия в виде:

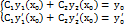
Постоянные 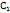и 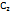из этой системы линейных алгебраических уравнений определяются однозначно, так как определитель этой системы есть значение определителя Вронского для линейно независимых решений лоду при :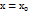

,

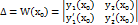а такой определитель, как мы видели в предыдущем параграфе, отличен от нуля.

Билет 24

Билет 25

Пусть плоская кривая АВ задана уравнением у = f( x), a ≤ x ≤ b, где

f ( x) – непрерывная вместе со своей производной на отрезке [ а, b] функция. Разобьем кривую АВ на n произвольных частей точкамиА = М₀, М₁, М₂, … , M_{i - 1}, M_i, …, M_n = B. Соединив эти точки хордами, получим некоторую вписанную ломанную линию, длину которой обозначим через Р.
Обозначим через l_i длину одного звена M_{i - 1}M_i ломаной линии, а через μ — длину наибольшего из ее звеньев: .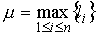
Определение. Число L называется пределом длин ломаных Р при μ → 0, если для любого как угодно малого ε > 0 существует δ > 0 такое, что для всякой ломаной, у которой μ < δ, выполняется неравенство | L − P | < ε.
Если существует конечный предел L длин ломаных Р вписанных в кривую при μ → 0, то этот предел называется длиной дуги АВ:

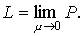
Доказательство. Обозначим через x_i и f ( x_i) координаты точек М_i. Длина одного звена ломаной равна

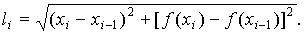
По формуле Лагранжа конечных приращений имеем

,

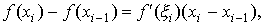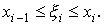
Следовательно, 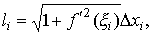, Δ x_i = x_i − x_{i − 1}. Таким образом, длина ломаной равна

.

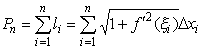Так как функция 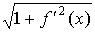непрерывна на [а, b], то предел суммы Р _n при 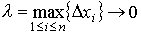существует. Так как λ ≤ μ и λ → 0 при μ → 0, то

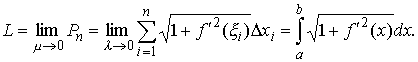
Симметричная форма системы дифференциальных уравнений

Для нахождения первых интегралов иногда удобно записать исходную систему в т.н. симметричной форме:

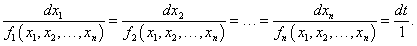
Здесь предполагается, что функции f₁, f₂, ..., f_n в знаменателях не равны нулю в области определения D∈ℜⁿ.

В такой записи некоторые пары отношений могут допускать интегрирование, например, методом разделения переменных. Другой способ решения системы в симметричной форме заключается в использовании свойства равных дробей

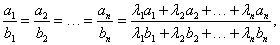
где предполагается, что λ₁b₁ + λ₂b₂ + ... + λ_nb_n ≠ 0, а числа λ₁, λ₂, ..., λ_n выбираются таким образом, чтобы числитель представлял собой дифференциал знаменателя или был равен нулю.

Билет 26

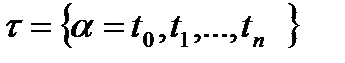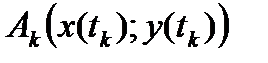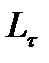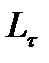
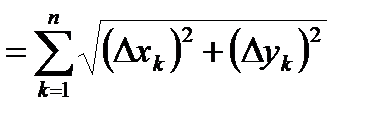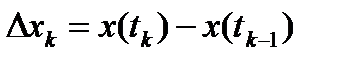Для ее доказательства заметим, что разбиение порождает разбиение дуги кривой точками и длину ломанной , где и 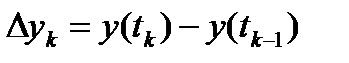.По теореме о среднем для производной существует набор 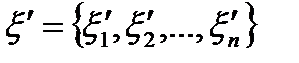и 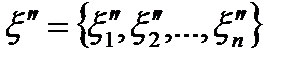точек на отрезках 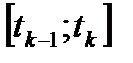, для которых 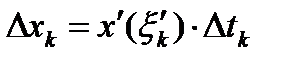и 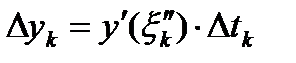. Тогда длина ломаной равна .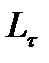

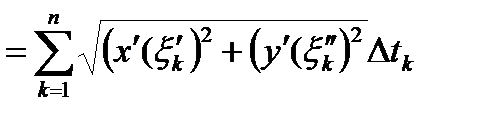Полученное выражение по форме отличается от интегральной суммы функции 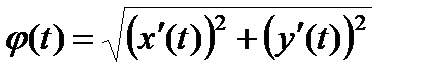, поскольку наборы 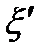и 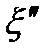,вообще говоря , различные.

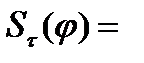
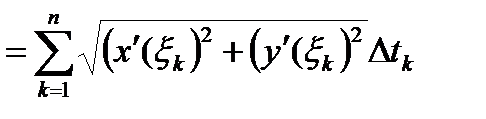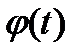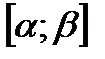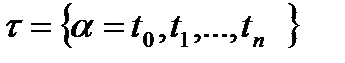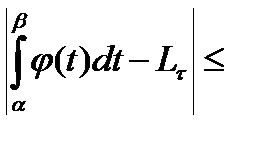
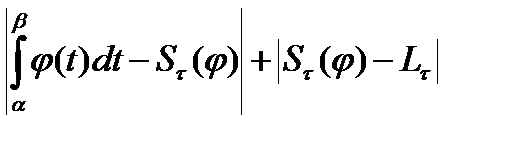Если интегральная сумма функции на отрезке соответствующая разбиению ,то . Для любого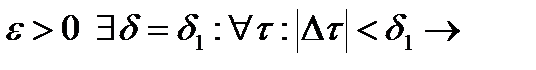 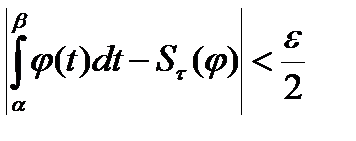. Вторая часть оценки использует « неравенство треугольника» .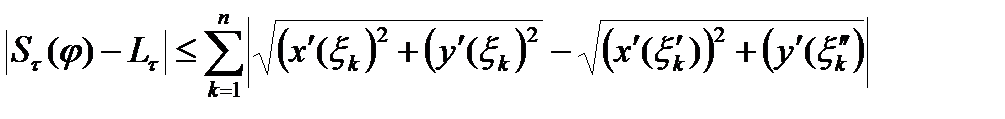

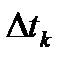
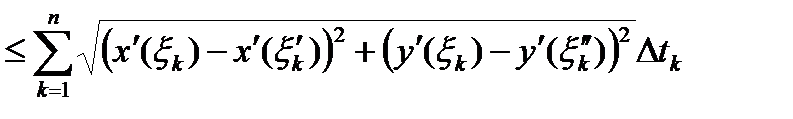
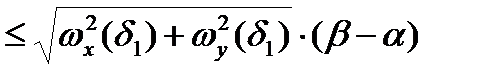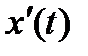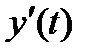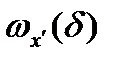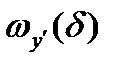В предположении непрерывности производных и колебания и - бесконечно малые функции в точке 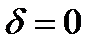, поэтому существует 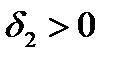такое , что 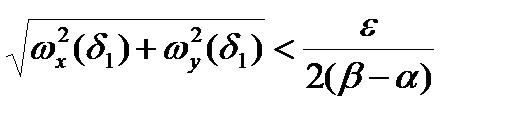для любых 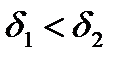. Тогда для разбиений

.

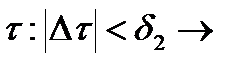
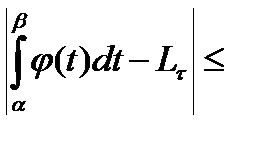
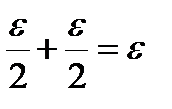Билет 27

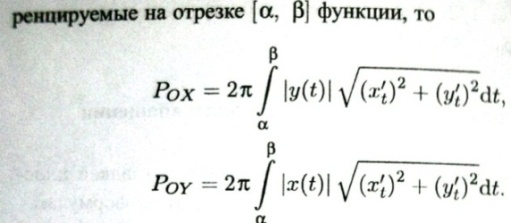
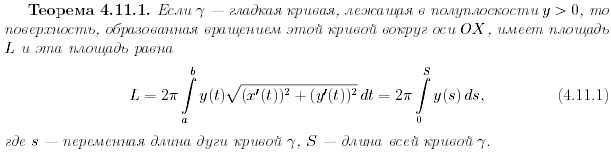
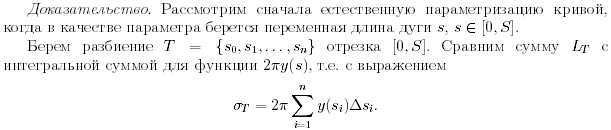
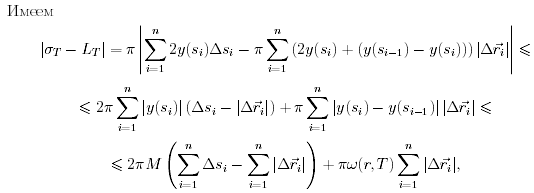
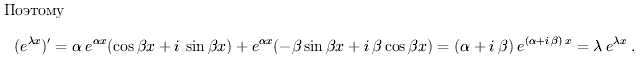
Билет 28

Д-во

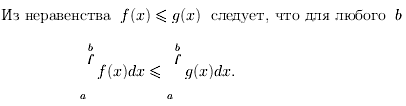
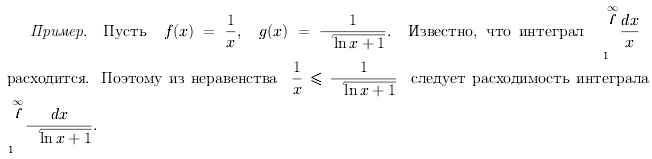
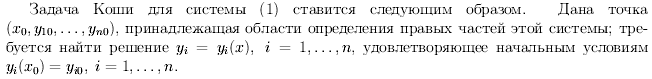
Билет 29

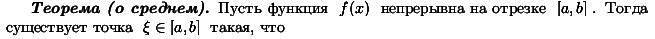
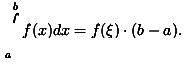
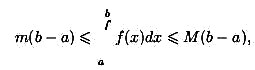или