4.5.3. Контрольные вопросы для самопроверки
1. Какой случай сложного сопротивления стержня называется косым изгибом?
2. Какие напряжения возникают в поперечном сечении стержня при косом изгибе и как они определяются?
3. Как определяется положение нейтральной оси при косом изгибе?
4. В каких точках поперечного сечения возникают наибольшие нормальные напряжения при косом изгибе?
5. Как определяются перемещения поперечных сечений и проводится расчет балок на жесткость при косом изгибе?
6. Какой случай напряженного состояния реализуется в точках контура круглого сечения при изгибе с кручением?
7. Какие случаи напряженного состояния реализуются в точках контура прямоугольного сечения при изгибе с кручением?
8. Как определяются перемещения поперечных сечений и проводится расчет балок на жесткость при изгибе с кручением?
9. Какой знак имеют нормальные напряжения в центре тяжести сечения при внецентренном растяжении или сжатии?
10. Как определяется очертание и положение нейтральной оси при внецентренном растяжении-сжатии стержня?
11. Как проводится подбор размеров круглого и круглого кольцевого поперечных сечений в общем случае сложного сопротивления стержня?
12. Как проводится подбор размеров прямоугольного поперечного сечения в общем случае сложного сопротивления стержня?
4.6. Расчет центрально-сжатого стержня на устойчивость. Построение эпюр внутренних усилий и определение перемещений сечений плоского ломаного стержня и стержневой системы
4.6.1. Задача 6.1

| Рис. 4.37 |
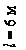 Сжатая стойка, расчетная схема которой представлена на рис. 4.37, выполнена из прокатных элементов, материал Ст3,
Сжатая стойка, расчетная схема которой представлена на рис. 4.37, выполнена из прокатных элементов, материал Ст3,
R = 200 МПа.
Требуется:
1. С помощью таблицы коэффициентов продольного изгиба подобрать поперечное сечение стойки заданной формы.
2. Подобранное сечение проверить на прочность при наличии ослабления Ant = 0,85Abr.
3. Определить критическую силу и коэффициент запаса устойчивости.
4. Для подобранного сечения построить график зависимости критической силы и критического напряжения от длины и гибкости стержня, изменяя гибкость от 0 до 200.
Решение
Расчет центрально-сжатого стержня на устойчивость производится методом последовательных приближений.
1. Зададим коэффициент продольного изгиба в первом приближении φ = 0,6. Выразим из условия устойчивости (3.58) площадь поперечного сечения стойки:
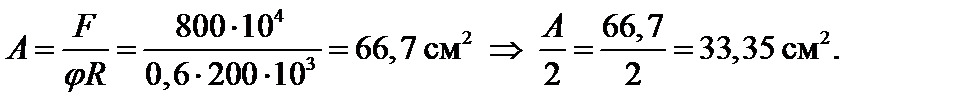
По сортаменту выбираем швеллер с ближайшим значением площади, а именно 2[ № 27: А = 35,2 см2, Iy = 262 см4, iz = 10,9 см, b = 95 мм, z0 = 2,47 см.
В данном случае потеря устойчивости будет происходить в плоскости xO y, т.к. очевидно, что 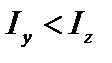 =>
=> 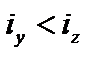 .
.
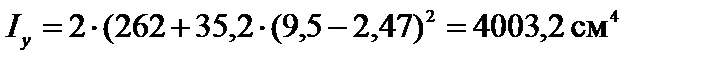 ,
,
| Рис. 4.38 |






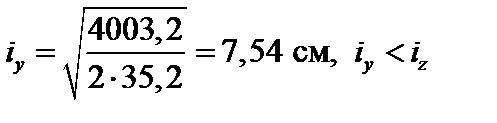 ,
,

С помощью СНиП определяем значение коэффициента продольного изгиба φ:
λ = 50 – φ = 0,869,
λ = 60 – φ = 0,827.
Для λ = 55,7 определим φ с помощью интерполяции:
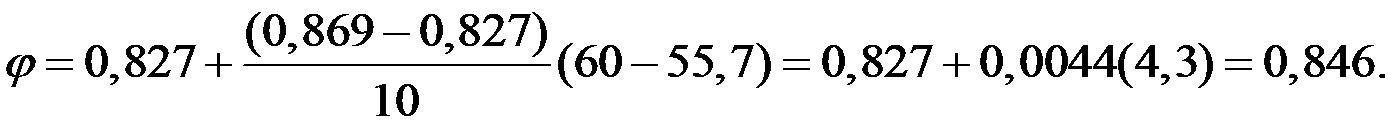
Выполним проверку условия устойчивости (3.58):
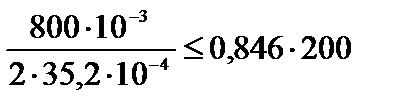 ,
,
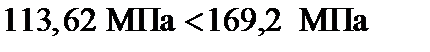 .
.
Условие (3.58) выполняется, но имеет место большое недонапряжение. Выполним еще одну итерацию. Во втором приближении коэффициент продольного изгиба находится как среднеарифметическое значение между заданным в начале предыдущей итерации (φ = 0,6) и вычисленным для швеллера № 27 (φ = 0,846):
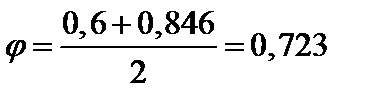 .
.
Последующие вычисления аналогичны вычислениям, изложенным выше.
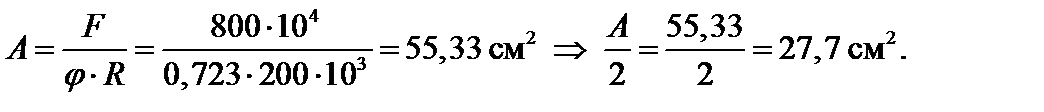
По сортаменту выбираем швеллер с ближайшим значением площади, а именно 2[ № 22: А = 26,7 см2, Iy = 151 см4, iz = ix = 8,89 см, b = 82 мм, z0 = 2,21 см.
Определим значение момента инерции относительно оси y:
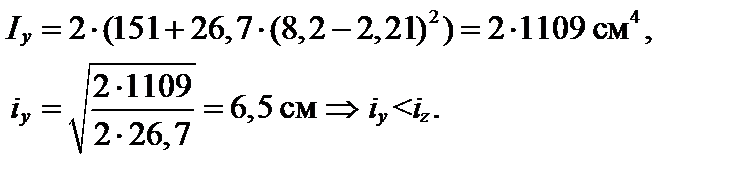

С помощью СНиП определим значение коэффициента продольного изгиба φ:
λ = 60 – φ = 0,827,
λ = 70 – φ = 0,782.
Для λ = 64,6 определим φ с помощью интерполяции:
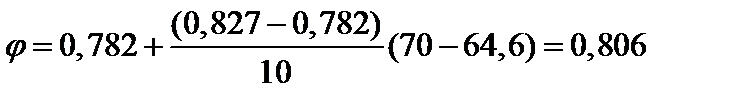 .
.
Выполним проверку условия устойчивости (3.58):
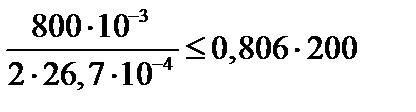 ,
,
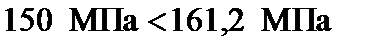 .
.
Условие (3.58) выполняется, но имеет место небольшое недонапряжение. Проверим 2[ № 20: А = 23,4 см2, Iy = 113 см4, iz = ix = 8,07 см, b = 76 мм, z0 = 2,07 см.
Определим значение момента инерции относительно оси y:
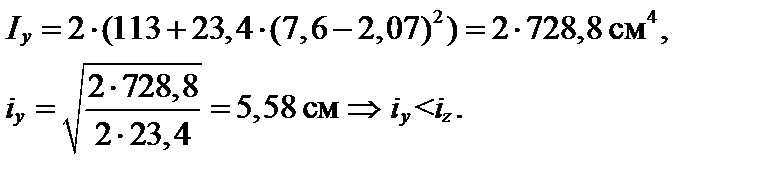
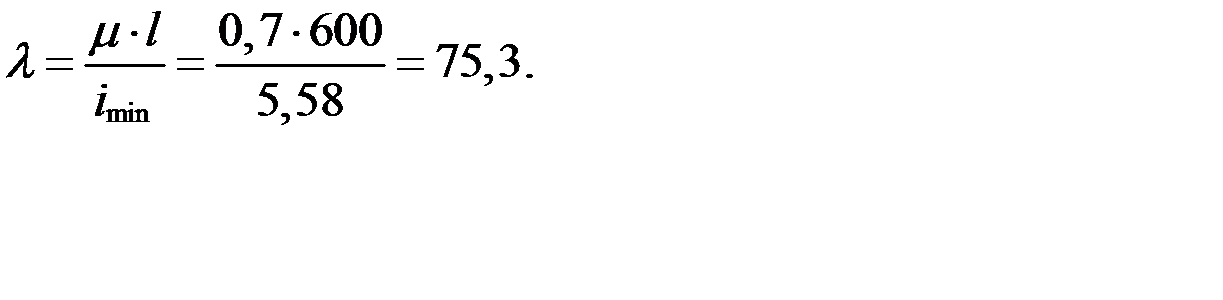
С помощью СНиП определим значение коэффициента продольного изгиба φ:
λ = 70 – φ = 0,782,
λ = 80 – φ = 0,734.
Для λ = 75,3 определим φ с помощью интерполяции:
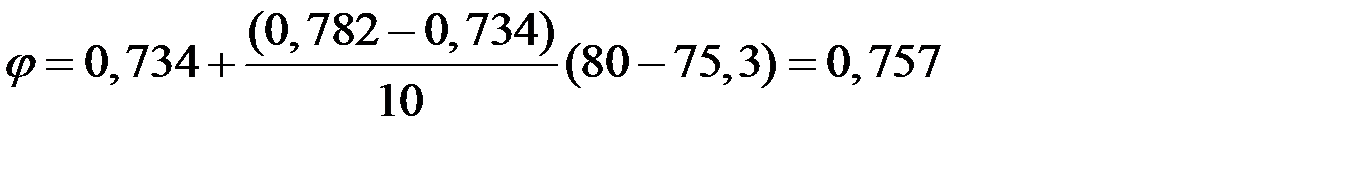 .
.
Выполним проверку условия (3.58):
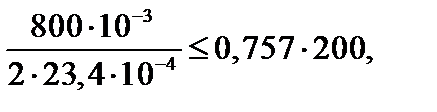
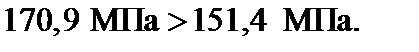
Таким образом, условие устойчивости (3.58) не выполняется для 2[ № 20, поэтому окончательно принимаем 2[ № 22. Расчет на устойчивость закончен.
2. Выполним проверку прочности подобранного сечения при наличии ослабления Ant = 0,85 · Abr:
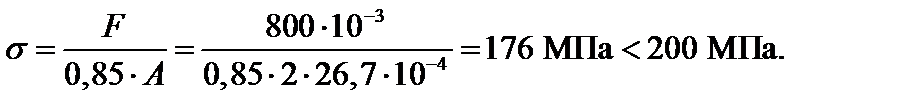
Сечение, подобранное из условия устойчивости, удовлетворяет условию прочности, корректировку сечения проводить не требуется.
3. Определим критическую силу и коэффициент запаса устойчивости.
Предельная гибкость для Ст3
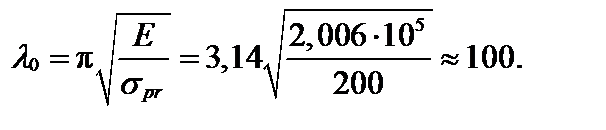
Сравним гибкость, найденную в п. 1 расчета на устойчивость, с предельной гибкостью: λ = 64,6 < 100. В случае, когда гибкость стержня меньше предельной гибкости, определение критической силы производят с помощью эмпирической зависимости Ясинского (3.56):
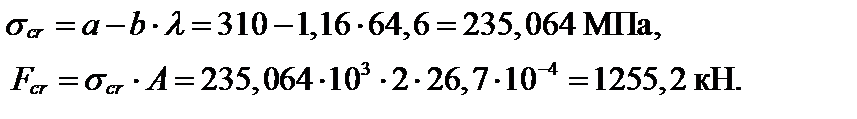
Определим коэффициент запаса устойчивости:
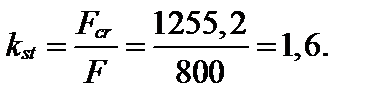
4. Для подобранного сечения построим график зависимости критической силы и критического напряжения от длины и гибкости стержня, изменяя гибкость от 0 до 200 (рис. 4.39).






















Рис. 4.39
Поперечное сечение состоит из двух прокатных профилей 2[ № 22: площадь одного профиля А = 26,7 см2, минимальный момент инерции всего сечения, состоящего из двух профилей, Imin = 2218 см4, минимальный радиус инерции imin = 6,5 см.
Задавая гибкость стержня 62,4 ( 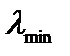 для Ст3), 100, 150, 200, будем получать соответствующую этим гибкостям длину стержня:
для Ст3), 100, 150, 200, будем получать соответствующую этим гибкостям длину стержня:

В интервале 61,4 ≤ λ ≤ 100 определение критических значений следует производить с помощью формулы Ясинского:

В интервале 100 ≤ λ ≤ 200 определение критических значений следует производить с помощью формулы Эйлера:
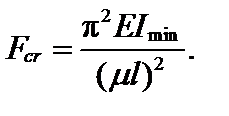
Для удобства сведем результаты расчета в таблицу.
| λ | l, м | s cr, МПа | Fcr, кН |
| 61,4 | 5,7 | 240 | 1281,6 |
| 64,6 | 6 | 235,04 | 1255,2 |
| 100 | 9,3 | 196 | 1046,6 |
| 150 | 13,95 | 85,9 | 458,7 |
| 200 | 18,6 | 48,3 | 258 |



| Рис. 4.40 |
 4.6.2. Задача 6.2
4.6.2. Задача 6.2
Сжатая стойка, расчетная схема и поперечное сечение которой показаны на рис. 4.40, выполнена из материала Ст3. Коэффициент запаса устойчивости kst = 1,3.
Требуется: из расчета на устойчивость определить допустимое значение нагрузки F.
Решение
Допустимое значение нагрузки находят по формуле
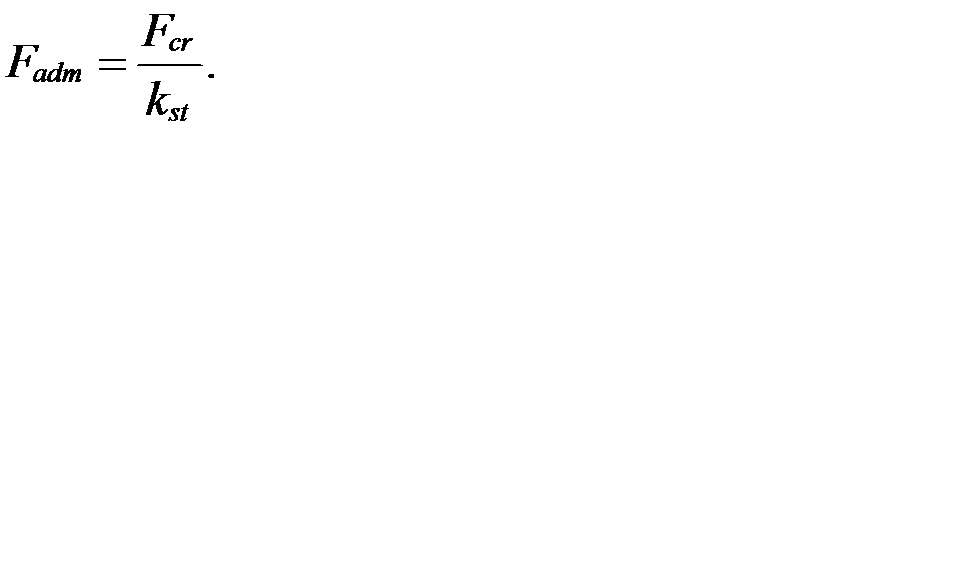
Критическую силу Fcr находим либо по формуле Эйлера (3.51), либо с помощью зависимости Ясинского (3.56). Выбор формулы зависит от величины гибкости стержня.


| z |
| y |

Определим минимальный радиус инерции заданного сечения. Очевидно, что iz < iy, т.к. ось z перпендикулярна короткой стороне се-
чения.
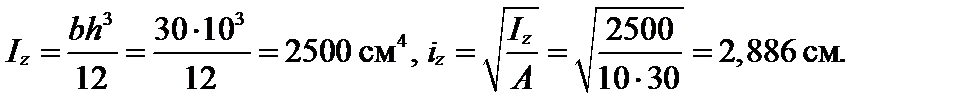
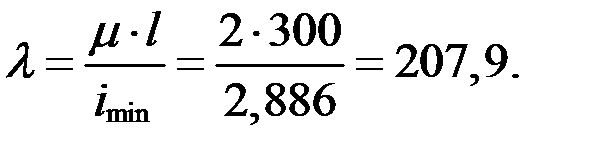
Предельная гибкость для Ст3 λ0 ≈ 100. Отсюда λ > λ0, тогда критическую силу определим с помощью формулы Эйлера:
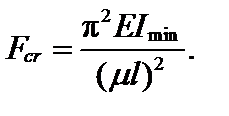
В данном случае для Ст3 Е = 2∙105 МПа.
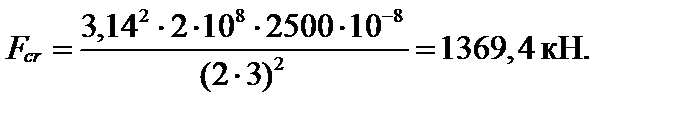
Осталось определить только допустимое значение нагрузки.
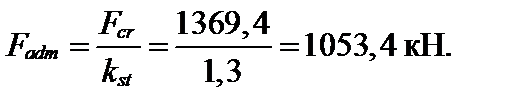
4.6.3. Задача 6.3
Для ломаного стержня, расчетная схема которого приведена на рис. 4.41, построить эпюры внутренних усилий и определить полное линейное перемещение сечения 1-1 и угол поворота сечения 2-2 от заданной нагрузки.
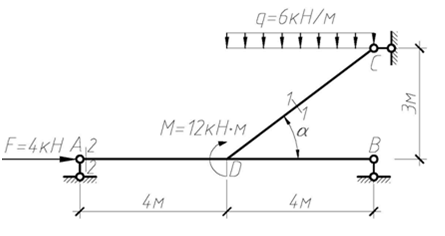



Рис. 4.41
1. Построение эпюр изгибающих моментов, поперечных и продольных сил от заданной нагрузки
Отбросив опорные связи и заменив их реакциями этих связей (рис. 4.42), составляем уравнения равновесия, из которых находим реакции опор.
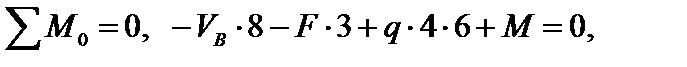
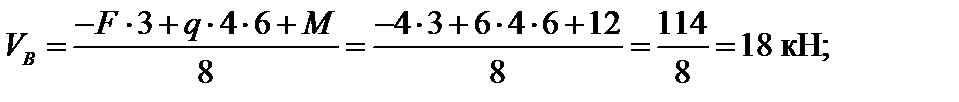
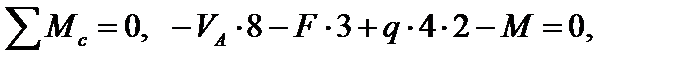
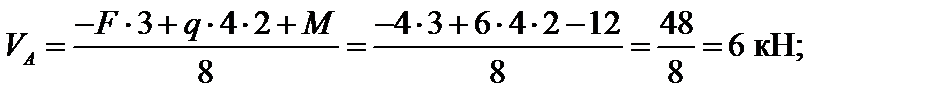
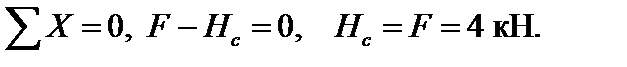
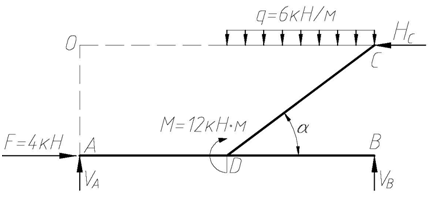
Рис. 4.42
При действии заданной нагрузки ломаный стержень имеет 3 грузовых участка AD, BD, CD. Для построения эпюр внутренних усилий на участке CD, применяя метод сечений, рассмотрим равновесие отсеченной части, показанной на рис 4.43. Выберем начало координат в точке С, ось х локальной системы координат направим вдоль наклонного участка С D влево. Тогда для рассматриваемого участка 0 ≤ х ≤ 5 м. Заменив в сечении действие отброшенной части внутренними усилиями М F(x), Q (x), NF(x) положительного направления, составим уравнения равновесия для оставленной части:
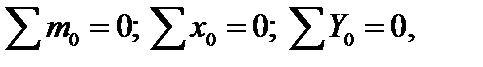
из которых находим:
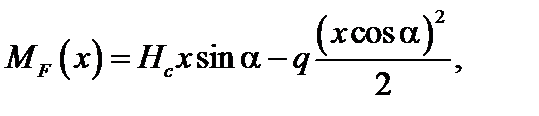
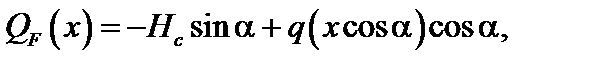
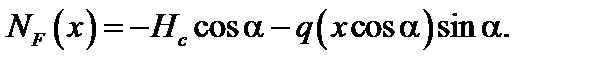
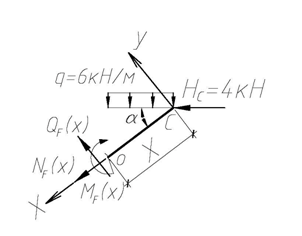
Рис. 4.43
Из полученных выражений видно, что эпюра М F(x) на участке очерчивается квадратной параболой, а эпюры QF(x), NF(x) – наклонными прямыми. Находим значения внутренних усилий в характерных сечениях участка, учитывая, что sin a = 0,6; cos a = 0,8.
При x = 0
MF = 0, QF = –4·0,6 = –2,4 кН, NF = –4·0,8 = –3,2 кН.
При x = 2,5 м
MF = 4·2,5·0,6 – 6 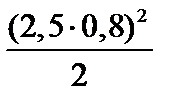 = 6 – 12 = –6 кН·м.
= 6 – 12 = –6 кН·м.
При x = 5 м
MF = 4·5·0,6 – 6 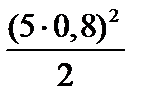 = 12 – 48 = –36 кН·м,
= 12 – 48 = –36 кН·м,
QF = –4·0,6 + 6(5·0,8)·0,8 = –2,4 + 19,2 = 16,8 кН,
NF = –4·0,8 – 6(5·0,8)·0,6 = –3,2 – 14,4 = –17,6 кН.
По найденным значениям строятся эпюры внутренних усилий на участке С D. Аналогично определяются изгибающие моменты, поперечные и продольные силы на остальных участках. Эпюры М F(x), Q F(x) и NF(x) приведены на рис. 4.44. Отметим, что эпюра изгибающих моментов строится на растянутых волокнах и знаки на ней не ставятся.
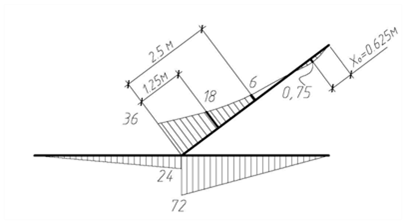
| Эп. MF, кН·м |
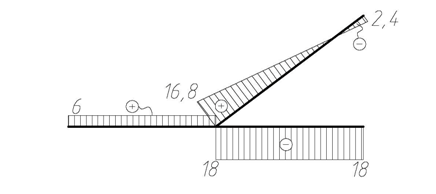
| Эп. QF, кН |
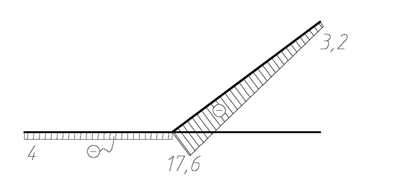
| Эп. NF, кН |
Рис. 4.44
Проверка равновесия узла D показана на рис. 4.45.
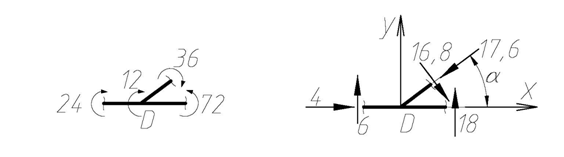
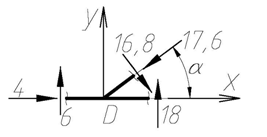


 Рис. 4.45
Рис. 4.45
2. Определение линейного перемещения сечения 1-1
Перемещения определяем, пренебрегая влиянием поперечных и продольных сил. Поэтому для вспомогательных единичных состояний строим только эпюры изгибающих моментов.
Полное линейное перемещение сечения 1-1 может быть вычислено, если будут найдены горизонтальная и вертикальная составляющие этого перемещения.
Чтобы найти значение горизонтальной составляющей полного перемещения сечения 1-1, рассматриваем вспомогательное единичное состояние ломаного стержня (состояние i = 1), прикладывая горизонтальную силу F1 = 1 в сечении 1-1 (рис. 4.46).
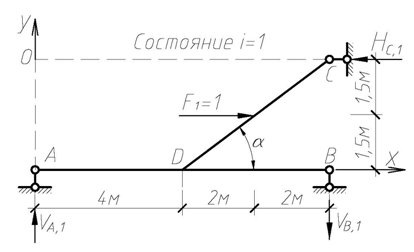
Рис. 4.46
Находим опорные реакции:
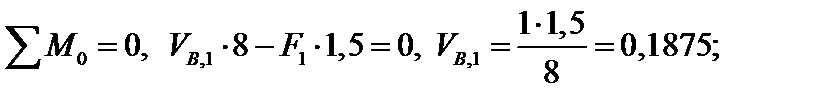
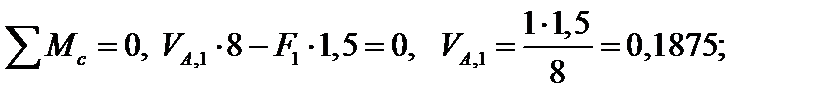
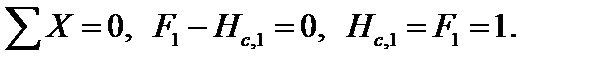
Строим эпюру изгибающих моментов М1 (рис. 4.47), проверяем равновесие узла D по моментам (рис. 4.48).
| Эп. M1 (м) |
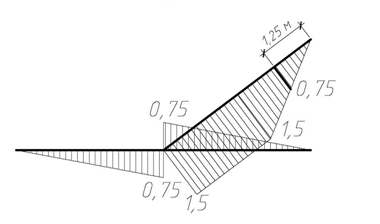
Рис. 4.47
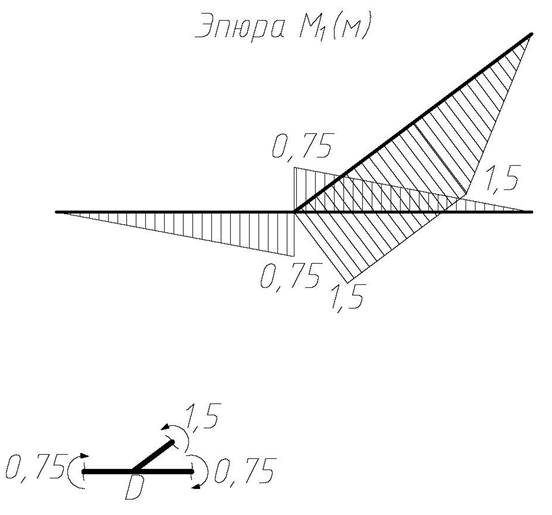
Рис 4.48
Определяем горизонтальные перемещения сечения 1-1, перемножая эпюру MF (см. рис. 4.44) с эпюрой M1 (см. рис. 4.47), учитывая заданное соотношение жесткостей сечений элементов при изгибе (при вычислении интегралов используется как формула Симпсона, так и правило Верещагина). Отметим, что на наклонном элементе ломаного стержня, учитывая характер эпюры М1, следует рассматривать два грузовых участка.
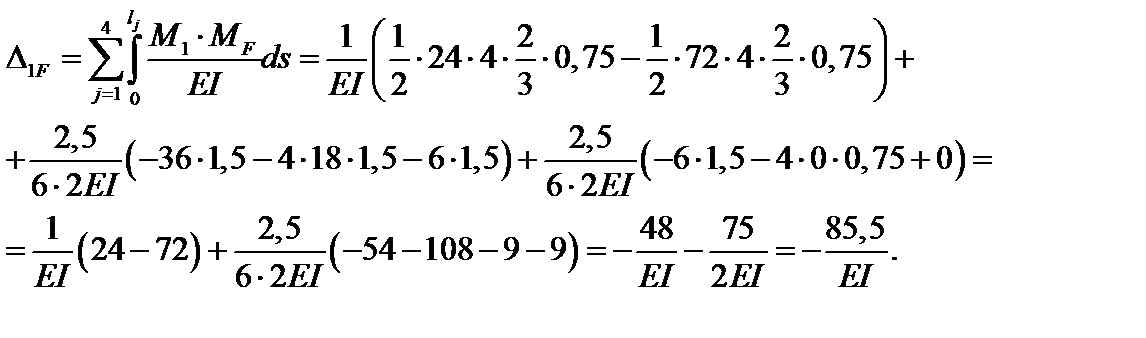
Знак «минус» полученного значения показывает, что горизонтальное перемещение сечения 1-1 противоположно направлению F1 = 1, т.е. направлено влево.
Для определения значения вертикальной составляющей полного перемещения сечения 1-1 рассматриваем вспомогательное единичное состояние ломаного стержня (состояние i = 2), прикладывая вертикальную силу F2 = 1 в сечении 1-1 (рис. 4.49).
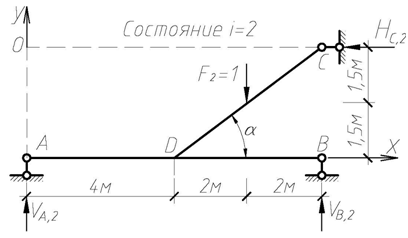
Рис. 4.49
Находим опорные реакции:
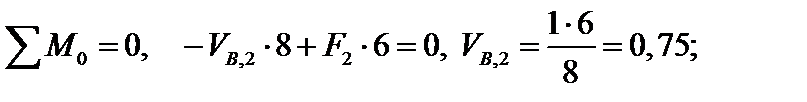
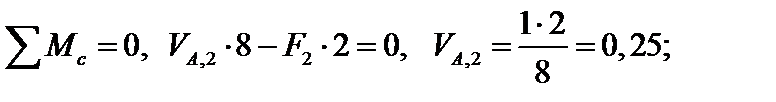
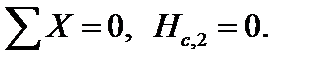
Проверка: 
Строим эпюру M2 и проверяем по моментам равновесие узла D (рис 4.50).
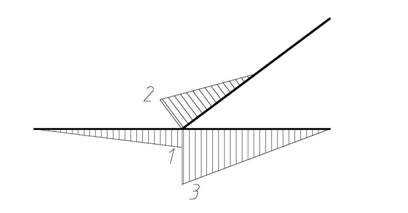
| Эп. M2 (м) |
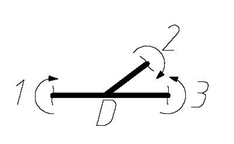
Рис. 4.50
Перемножая эпюры M2 и MF, получаем:
+ 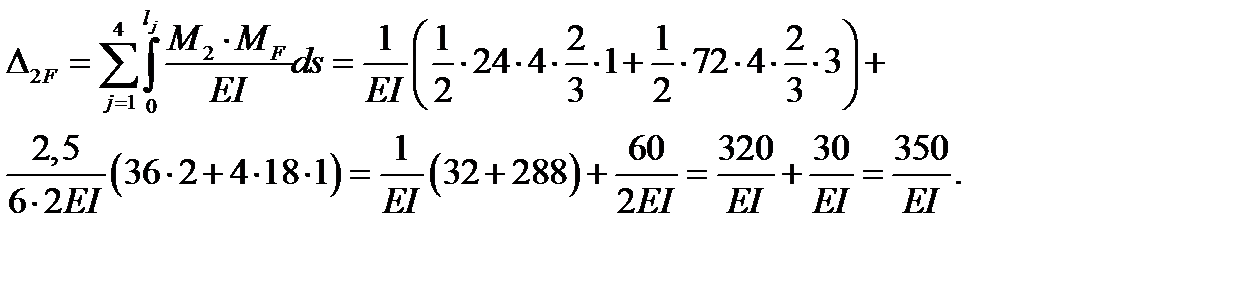
Направление вертикальной составляющей полного перемещения совпадает с направлением F2 = 1, т.е. направлено вниз.
Значение полного линейного перемещения сечения 1-1 равно
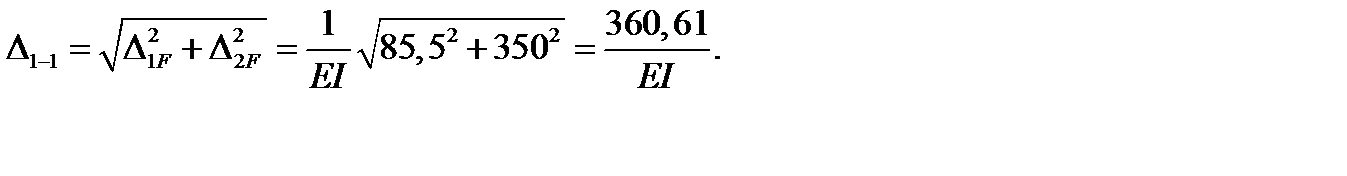
3. Определение угла поворота сечения 2-2
Для определения угла поворота сечения 2-2 рассматриваем вспомогательное единичное состояние ломаного стержня (состояние i = 3), прикладывая в сечении 2-2 момент М3 = 1 (рис. 4.51).
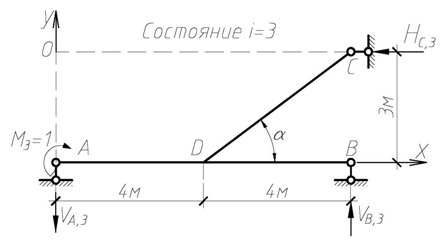
Рис. 4.51
Находим опорные реакции:
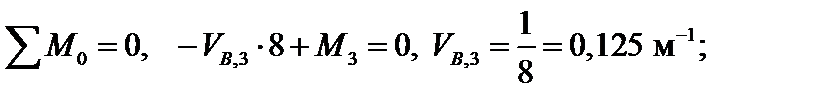
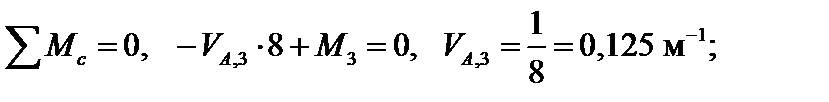
Строим эпюру изгибающих моментов 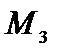 (рис. 4.52). Определяем искомое угловое перемещение:
(рис. 4.52). Определяем искомое угловое перемещение:
+ 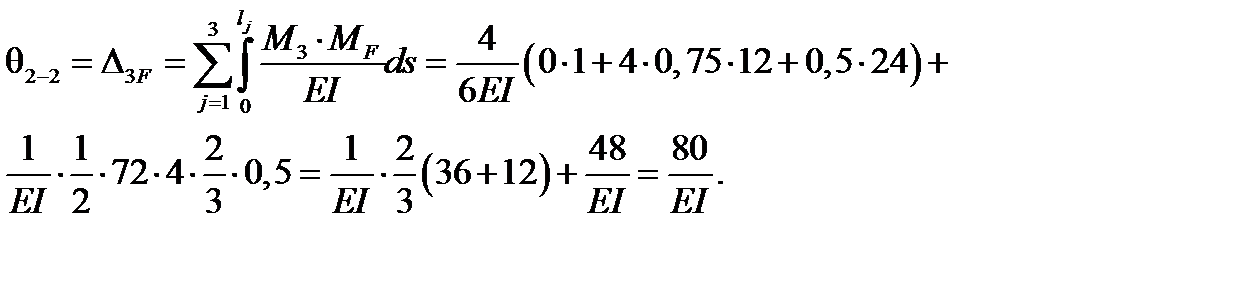
| Эп. M3 |
Рис. 4.52
Знак «плюс» θ2-2 показывает, что направление поворота сечения 2-2 совпадает с выбранным направлением М3 = 1, т.е. происходит по часовой стрелке.
4.6.4. Задача 6.4
Для плоской стержневой системы, расчетная схема которой приведена на рис. 4.53, требуется:
1. Построить эпюры изгибающих моментов, поперечных и продольных сил.
2. Определить вертикальное перемещение сечения 1-1 и угол поворота сечения 2-2.
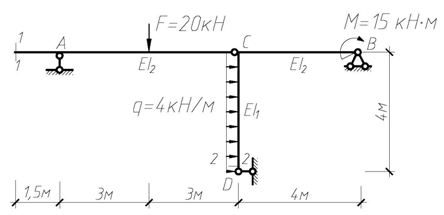
Рис. 4.53
Выполним кинематический анализ заданной системы. Проверим выполнение необходимого условия геометрической неизменяемости:
W = 3D – 2H – C – C0 ≤ 0.
Система состоит из двух дисков (D = 2), соединенных между собой примыкающим шарниром C (связью второго типа), т.е. H = 1. Линейные связи между дисками системы отсутствуют (С = 0). С неподвижным диском «земля» диски системы связаны четырьмя линейными связями (связями первого типа), т.е. С0 = 4. Определяем W = 3·2 – 2·1 – 0 – 4 = 0, т.е. необходимое условие геометрической неизменяемости выполняется.
Делаем структурный анализ. Диск BCD присоединен к «земле» тремя линейными связями (одна в точке D и две в точке B), оси которых не параллельны между собой и не пересекаются в одной точке (рис. 4.54). Следовательно, диск BCD вместе с диском «земля» образуют один диск. К этому неподвижному диску присоединен диск KAC с помощью линейной связи в точке A и шарниром в точке С, причем ось линейной связи не проходит через шарнир С. Таким образом, заданная система является геометрически неизменяемой, неподвижной и статически определимой (W = 0). На рис. 4.54 показана рабочая схема системы: на главную часть BCD опирается второстепенная часть K АС.
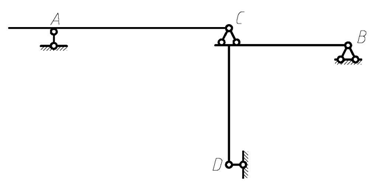
Рис. 4.54
Расчет системы ведется в следующей последовательности. Сначала рассчитываем второстепенную часть на приложенную к ней нагрузку (рис. 4.55), а затем главную часть, загружая ее как приложенной к ней заданной нагрузкой, так и давлением со стороны второстепенной части в шарнире C (рис. 4.56).
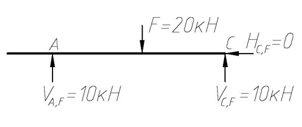
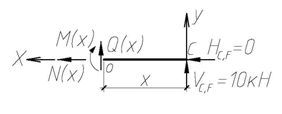
| 0 ≤ x ≤ 3 м |
Рис. 4.55
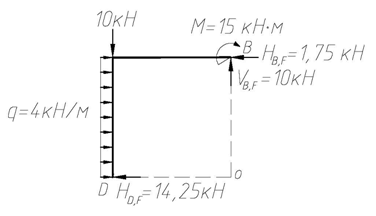
Рис. 4.56
На рис. 4.55 и 4.56 показаны и выписаны значения реакций, найденных из уравнений равновесия второстепенной и главной частей. Окончательно эпюры M, Q и N для заданной системы приведены на рис. 4.57.
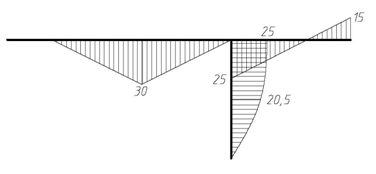
| Эп. MF (кН·м) |
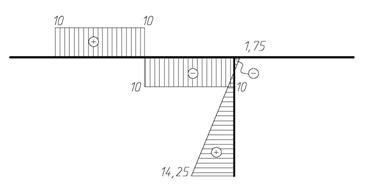
| Эп. QF (кН) |
| Эп. NF (кН) |
Рис. 4.57
Выполним проверку равновесия всей системы (рис. 4.58).
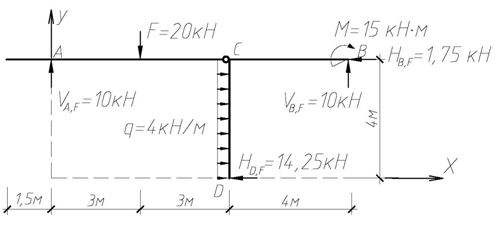
Рис. 4.58
SX = q · 4 – HB,F – HD,F = 4 · 4 – 1,75 – 14,25 = 16 – 16 º 0;
SY = –F + VA,F + VB,F = –20 + 10 + 10 = –20 + 20 º 0;
Smk = –VA,F · 1,5 + F · 4,5 + HD,F · 4 + M – q · 4 · 2 – VB,F · 11,5 =
= –10 · 1,5 + 20 · 4,5 + 14,25 · 4 + 15 – 4 · 4 · 2 – 10 · 11,5 =
= 162 – 162 º 0.
Для определения вертикального перемещения сечения 1-1 рассмотрим вспомогательное (единичное) состояние системы, прикладывая в сечении 1-1 вертикальную единичную силу (F1 = 1). Выполняя расчет системы в той же последовательности, что и на заданную нагрузку (рис. 4.59б, в), построим для этого состояния эпюру изгибающих моментов М1 (рис. 4.59г). Далее по формуле Максвелла–Мора, разбив систему на участки, перемножим эпюры М1 и М F, учитывая заданное соотношение жесткостей сечений при изгибе. При перемножении эпюр используем как правило Верещагина, так и формулу Симпсона. Получим:
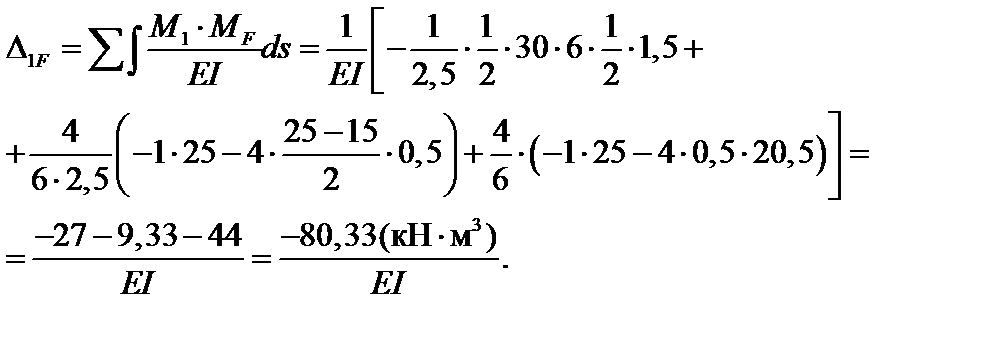
| а) |
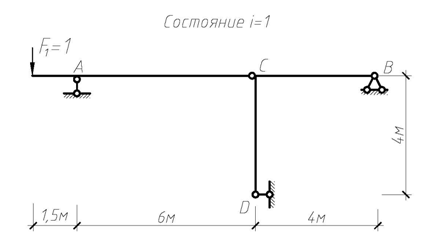
| Состояние i = 1 |
| б) |
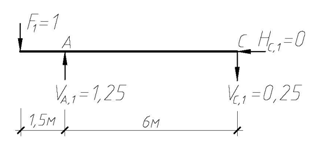
| в) |
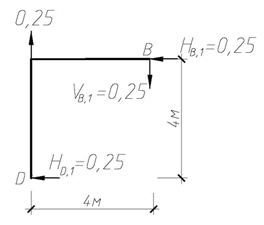
| г) |
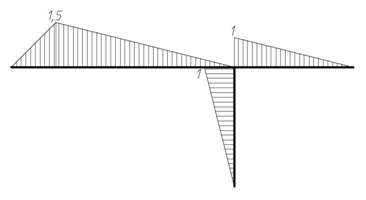
| Эп. M1 (кН·м) |
Рис. 4.59
Для определения угла поворота сечения 2-2 рассмотрим вспомогательное (единичное) состояние системы, прикладывая в сечении 2-2 единичный момент М2 = 1 (рис. 4.60). Построив эпюру изгибающих моментов М2 (рис. 4.60г), перемножим ее с эпюрой М F, также учитывая жесткости сечений при изгибе. Получим:
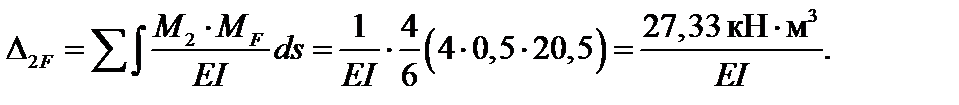
| Состояние i = 2 |
| а) |
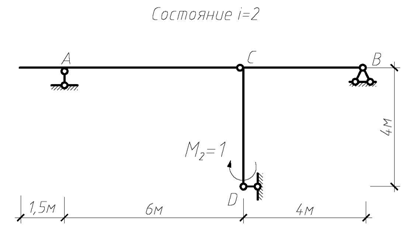
| б) |
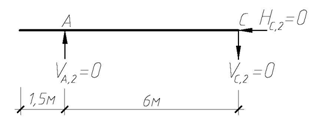
| в) |
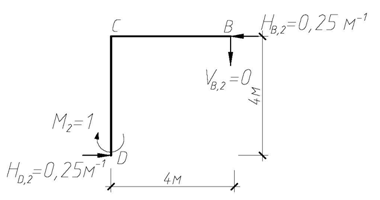
| г) |
| Эп. M2 (кН·м) |
Рис. 4.60
4.6.4. Контрольные вопросы для самопроверки








