Таким образом, на участке ① при рассмотрении сечения с координатой ось должна быть параллельна оси y1 (рис. 4.33).

Дата: 2025-05-25; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

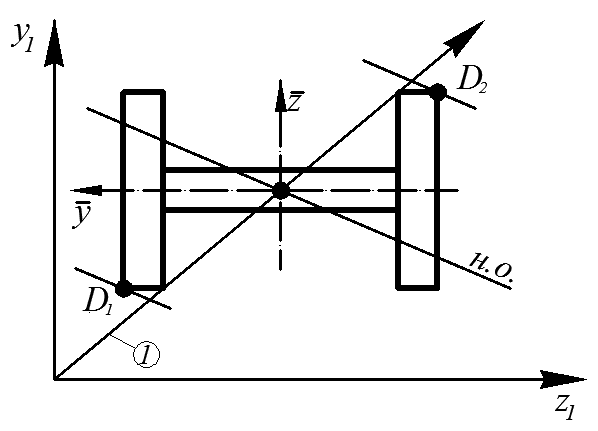Условие прочности по максимальным нормальным напряжениям в одной из опасных точек D₁, D₂ имеет вид:

. (3)

Рис. 4.33

После подстановок получим:

Отсюда

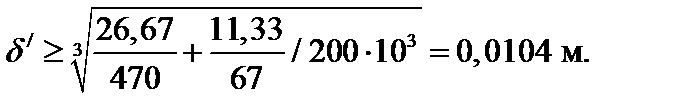
Для сечения с координатой 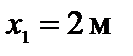поэтому расположение главных осей не имеет значения. Из условия (3) получим:

Отсюда

Таким образом, сечение с координатой 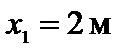оказалось более опасным. Окончательно выбираем параметр размеров

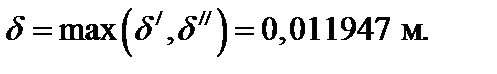
Участок ② – стержень испытывает общий случай сложного сопротивления (при отсутствии ). Усилия в опасном сечении с координатой x₂ = 2,4 м равны:

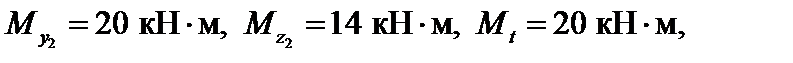
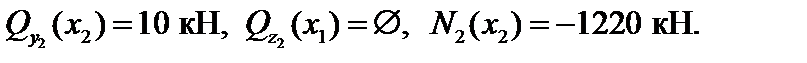
Максимальные по модулю нормальные и касательные напряжения (без учета составляющей от изгиба) в опасной точке на контуре сечения типа «б» определяются соотношениями

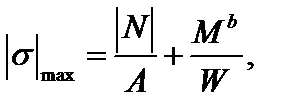
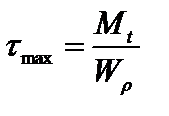, (4)

где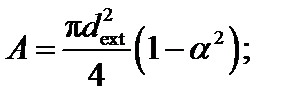

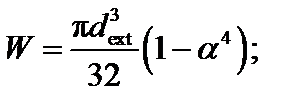
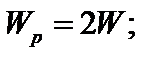
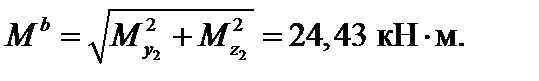
Условие прочности по 3-й теории прочности записывается в виде:

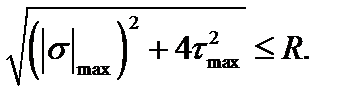(5)

Учитывая соотношения (4) и найденные значения внутренних усилий, запишем условие прочности (5) в виде:

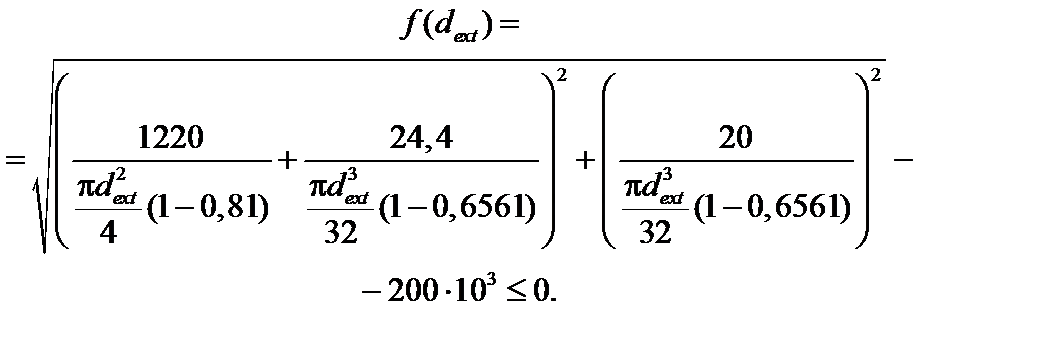(6)

Вычисляя f (d_ext) при различных значениях d_ext, получим: f (0,1) = 394847, f (0,2) = 103942,7, f (0,3) = 80342,5. Используя линейную аппроксимацию функции f (d_ext) в интервале [103942,7, –80342,5], получим приближенно корень уравнения (6), т.е. требуемый размер

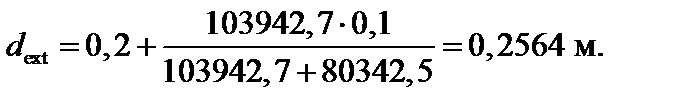
Полученное решение можно уточнить, вычисляя значения функции f (0,2564) и проводя повторную линеаризацию f (d_ext) в уточненном интервале, на концах которого функция f (d_ext) имеет значения разного знака.

4.5.2. Задача 5.2

Короткий жесткий стержень, поперечное сечение которого изображено на рис. 4.34, сжимается силой F, параллельной продольной оси стержня и проходящей через точку А поперечного сечения стержня. Стержень выполнен из материала, разносопротивляющегося растяжению и сжатию,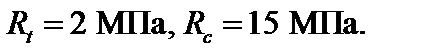

Требуется:

1. Найти положение нейтральной оси поперечного сечения стержня.

2. Из условий прочности найти величину допускаемой нагрузки [F].

3. При действии допускаемой нагрузки [F] построить эпюру s в поперечном сечении стержня.

4. Построить ядро рассматриваемого поперечного сечения.

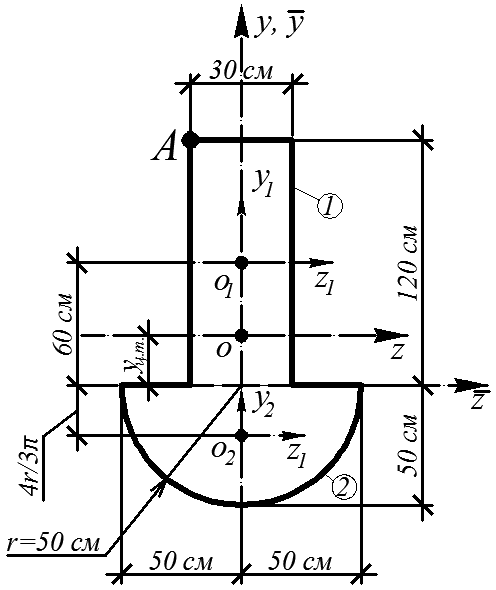
Рис. 4.34

Решение

1. Определение положения центра тяжести сечения

Рассматриваемое сечение имеет одну ось симметрии – y. Следовательно, ось y проходит через центр тяжести сечения и является главной центральной осью инерции. Для определения второй главной центральной оси инерции найдем положение центра тяжести сечения. Выберем вспомогательную систему координат (ось направлена вдоль горизонтального диаметра полукруга, ось 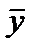совмещена с осью y).

Разобьем сечение на две части: j – прямоугольник 120´30 см, k – полукруг с радиусом r = 50 см; O₁, O₂ – центры тяжести фигур j, k. Пусть 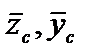– координаты центра тяжести O всего сечения. В силу симметрии 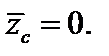Координата 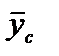определяется по формуле (3.17):

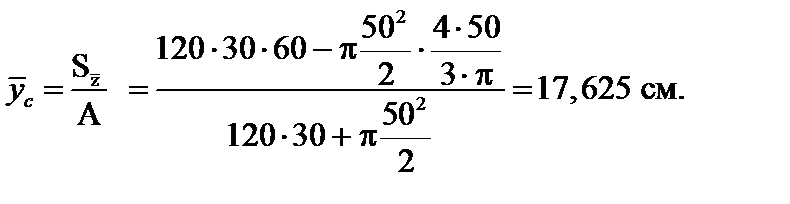
2. Определение главных центральных моментов инерции сечения

Оси y, z – главные центральные. Используя известные формулы для моментов инерции прямоугольника и полукруга, а также формулы перехода при параллельном переносе осей (см. п. 3.3.1.), получим:

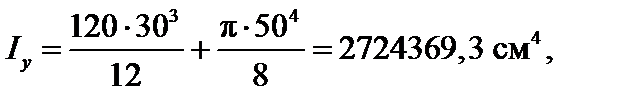
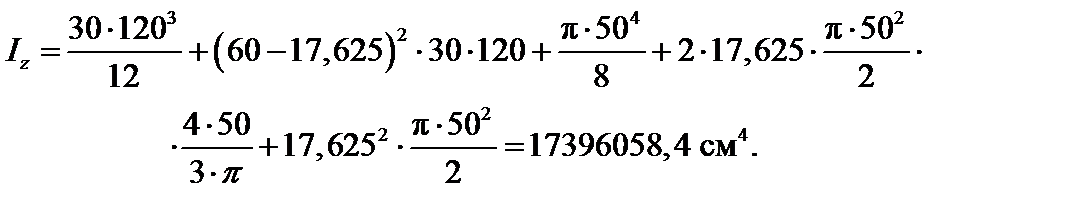
3. Определение нейтральной оси поперечного сечения стержня

Квадраты радиусов инерции рассматриваемого сечения равны

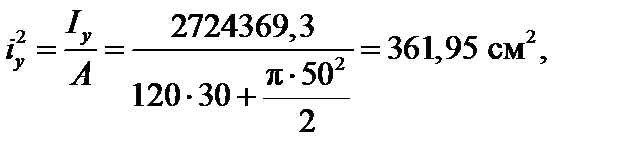
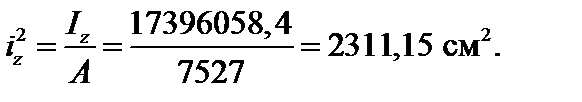
Согласно рис. 4.34 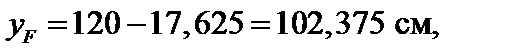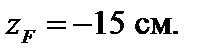Отрезки, отсекаемые нейтральной осью на координатных осях, вычисляются согласно соотношениям (3.46):

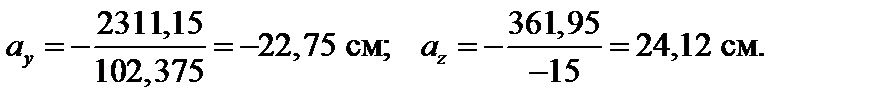
Положение нейтральной оси (н.о.) показано на рис. 4.35.

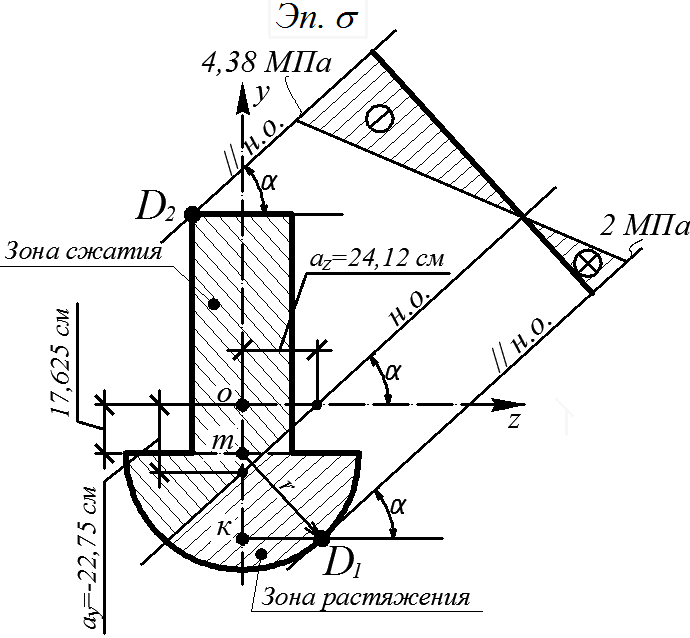
Рис. 4.35

4. Определение величины допускаемой силы [F] из условий прочности

Проводя касательные к сечению, параллельные нейтральной оси, находим наиболее удаленные от нейтральной оси (а, значит, и наиболее направленные) точки D₁, D₂ сечения в зонах растяжения и сжатия. Из рис. 4.35 следует, что

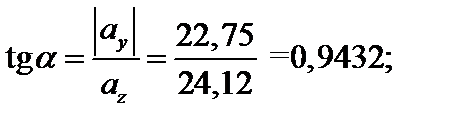
a = 43,325°, sin a = 0,686, cos a = 0,727.

Координаты опасных точек D₁, D₂ равны соответственно:

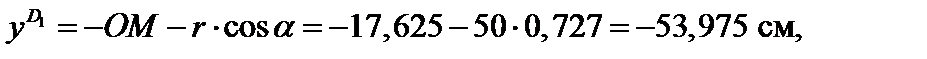
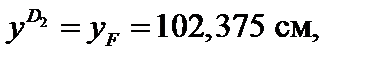
Условия прочности в опасных точках D₁, D₂ записываются в виде:

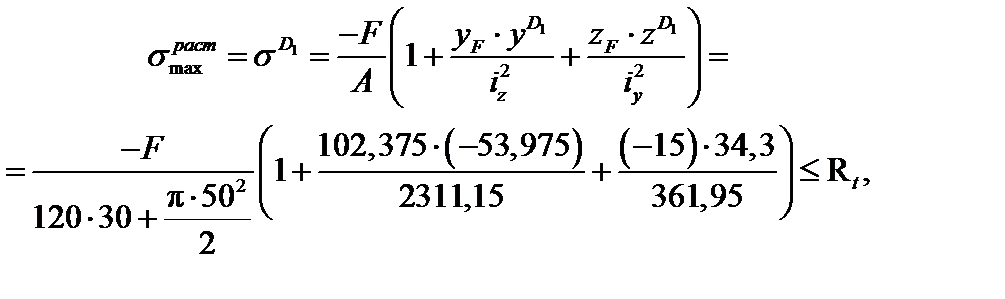
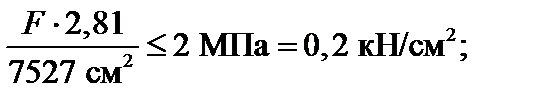(а)

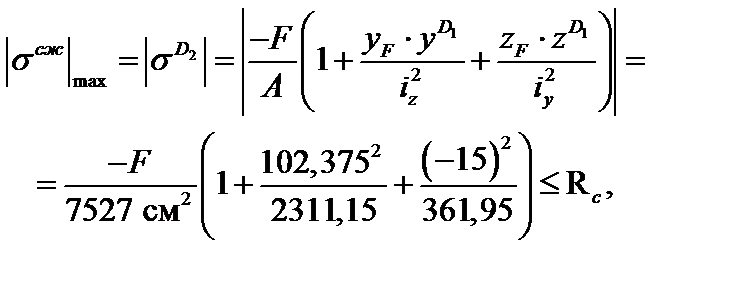
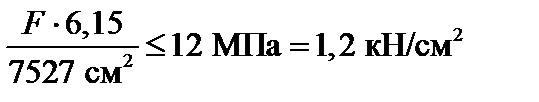. (б)

Из соотношений (а), (б) получим следующие условия для выбора допускаемой сжимающей силы:

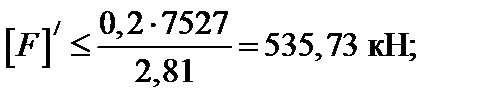
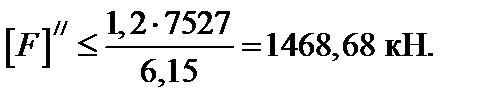
Принимаем окончательно

Эпюра нормальных напряжений в сечениях при найденной допускаемой силе представлена на рис. 4.35. Как следует из рисунка, материал стержня в зоне сжатия существенно недогружен.

5. Построение ядра рассматриваемого поперечного сечения стержня

Алгоритм построения ядра сечения заключается в следующем:

1) сечение описывается семейством касательных, для каждой из которых находятся отрезки 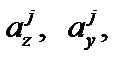j = 1, …, n (n – число касательных), отсекаемые ею на координатных осях;

2) для каждой из касательных (в предположении, что она является нейтральной осью) находятся координаты 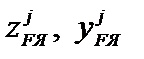точки приложения силы F, то есть точки границы ядра сечения по формуле (3.49). Результаты вычислений удобно заносить в таблицу;

3) соединяя полученные точки, построим границу ядра сечения, а следовательно, и само ядро сечения.

Касательные к рассматриваемому сечению показаны на рис. 4.36. В качестве примера на рис. 4.36 показаны отрезки, отсекаемые касательными 1, 2 на координатных осях.

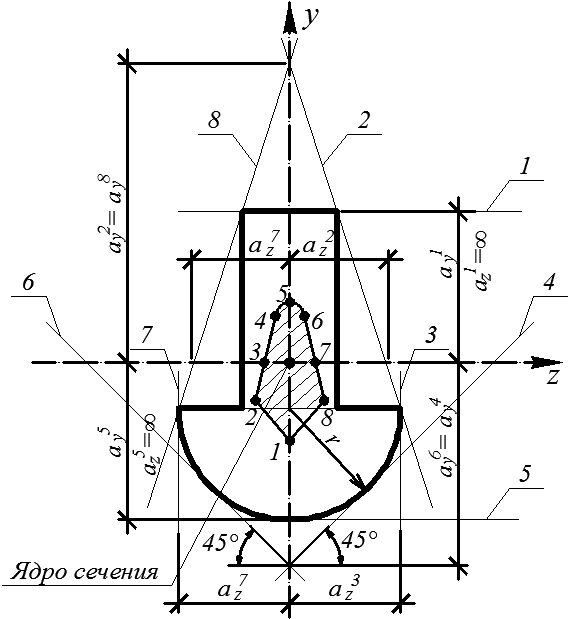
Рис. 4.36

Результаты вычислений 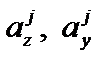, j = 1, …, n, приведены в таблице. Точки границы ядра сечения, соответствующие касательным j = 1, …, n на рис. 4.36, имеют те же номера.

К определению координат точек границы ядра сечения

№ касат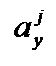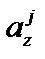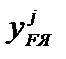.	, см	, см	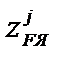, см	, см
1	102,375	∞	–22,57	0
2	153,8	29,86	–15,03	–12,12
3	∞	50	0	–7,24
4	–88,36	88,36	26,15	–4,1
5	–67,625	∞	34,15	0
6	–88,36	–88,36	26,15	4,1
7	∞	–50	0	7,24
8	153,8	–29,86	–15,03	12,12

Ядро рассматриваемого сечения – заштрихованная фигура на рис. 4.36. В том случае, когда при переходе касательной j в положение j + 1 она вращается вокруг полюса (например, при переходе касательной 1 в положение касательной 2), линия границы ядра сечения – прямая. В силу симметрии сечения точки 2 и 8, 3 и 7, 4 и 6 расположены симметрично относительно оси y.