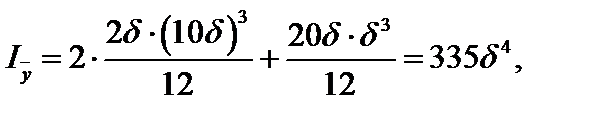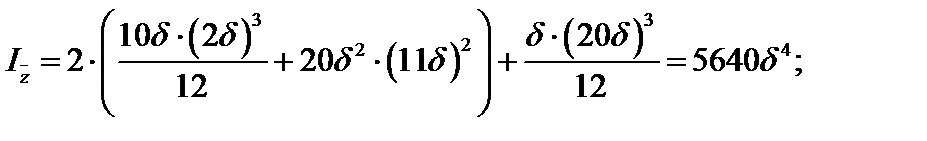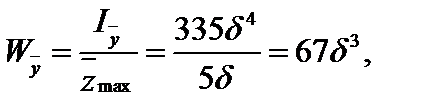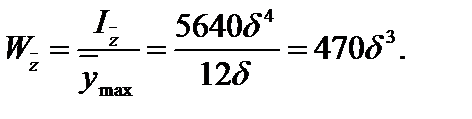По результатам расчета на ЭВМ построены эпюры прогибов и углов поворота q (см. рис. 4.22).
Проверим выполнение условия жесткости |u|max ≤ [u], где допускаемый прогиб [u] = (1/400)l = 8/400 = 0,020 м.
Максимальный по модулю прогиб определяем по эпюре прогибов (см. рис. 4.22):
[u]max = 0,01897 м.
Условие жесткости 0,01897 м < 0,020 м выполнено.
4.4.2. Контрольные вопросы для самопроверки
1. Какие моменты инерции поперечного сечения используются при расчете балки на прочность и жесткость и как они определяются?
2. Что называется грузовым участком?
3. Каковы особенности эпюр Q и M?
4. Как расположена нейтральная ось при прямом поперечном изгибе в упругой стадии?
5. По каким формулам определяются напряжения в точках поперечного сечения балки при прямом изгибе?
6. Как определить положение нейтральной оси при расчете балки по методу предельной несущей способности?
7. Как определяется пластический момент сопротивления сечения стержня при изгибе?
8. Какие дифференциальные зависимости между силовыми факторами при изгибе вы знаете?
9. Какие начальные параметры входят в выражения для перемещений, найденные по методу начальных параметров?
10. Из каких условий определяются начальные параметры?
4.5. Сложное сопротивление стержней
4.5.1. Задача 5.1
Для консольного ломаного стрежня, расчетная схема которого показана на рис. 4.28, требуется:
1. Построить эпюры внутренних усилий в поперечных сечениях стержня.
2. Определить форму сопротивления стержня на участках.
3. Подобрать сечения стержня на участках (см. рис. 4.28) из условий прочности; при наличии кручения на участке принять сечение типа «б»; при отсутствии кручения на участке принять сечение типа «а», выбрав рациональную ориентацию главных центральных осей инерции сечения. Расчетное сопротивление материала стержня на участках принять равным 200 МПа.
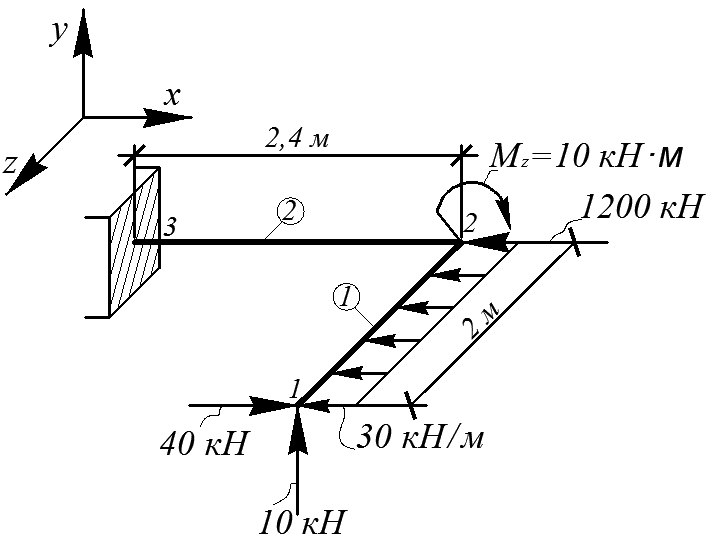
Рис. 4.28
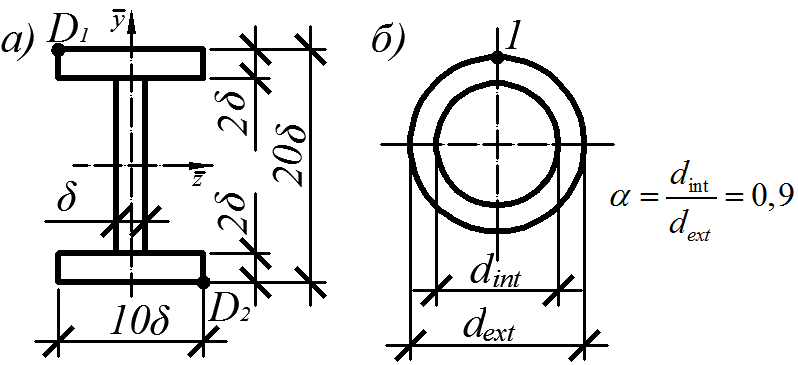
Рис. 4.29
Решение
1. Построение эпюр внутренних усилий в поперечных сечениях стержня
Обозначим узлы 1, 2, 3 рассматриваемого пространственного ломанного стержня и разделим его на участки ①, ② (см. рис. 4.28).
Рассмотрим каждый из участков, используя локальные системы координат xi, yi, zi, i = 1, 2, ось xi направлена вдоль продольной оси соответственного участка i.
Участок ①, 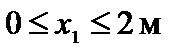
На рис. 4.30а, б изображена отсеченная часть стержня с заведомо положительными продольными и поперечными силами N1(x1), Qy1(x1), Qz1(x1), а также моментными усилиями – изгибающими моментами Mz1(x1), My1(x1) и крутящим моментом N1(x1), Mx1(x1) = Mt1(x1) в произвольном сечении к1 на участке ①.
| б) |
| а) |
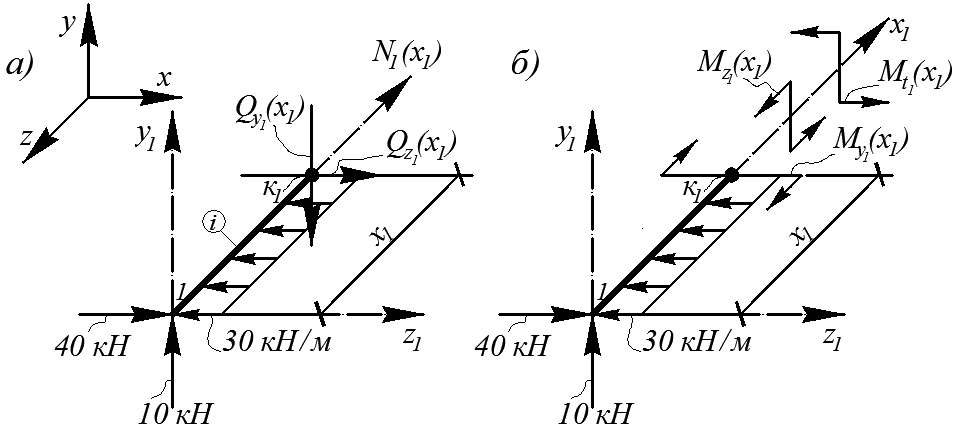
Рис. 4.30
Используя уравнения равновесия отсеченной части стержня (или соответствующее рабочее правило [3]), получим (единицы измерения – кН и кН·м):
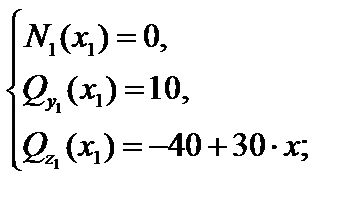
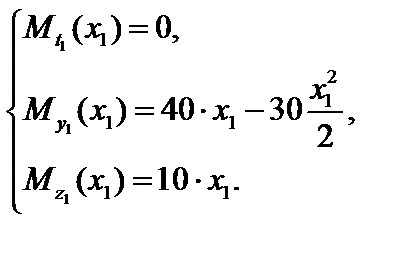 (1)
(1)
Участок ②, 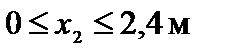
Выбирая произвольное сечение к2 на участке ② и отсекая свободную часть консоли (рис. 4.31), получим:
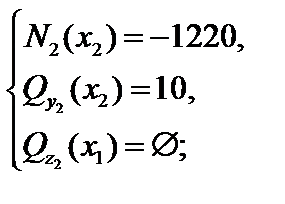
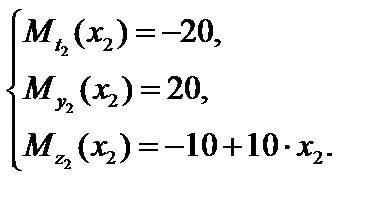 (2)
(2)
| z2 |
| у2 |
| х2 |
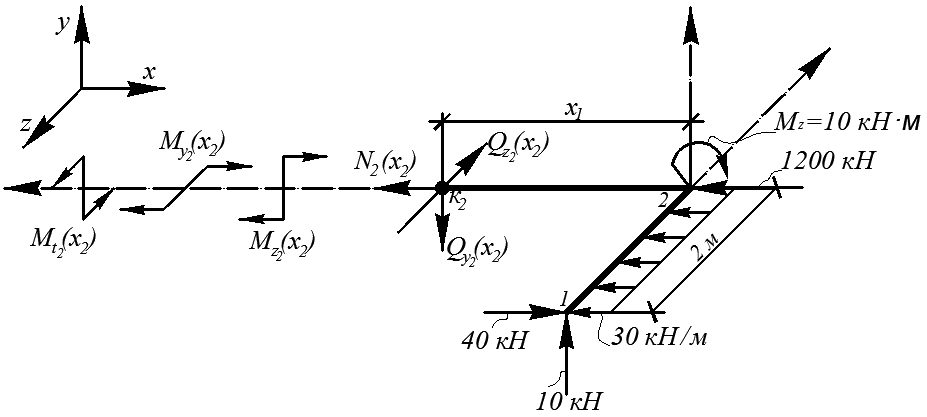
Рис. 4.31
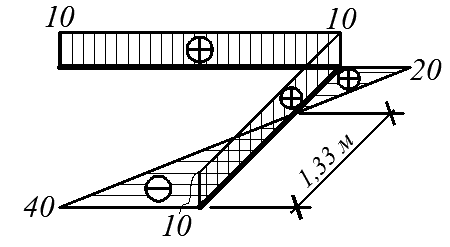
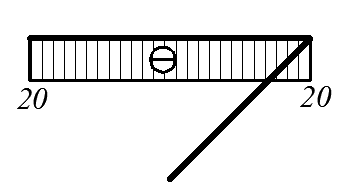
Используя полученные выражения (1), (2), строим эпюру внутренних усилий в сечениях пространственного ломаного стержня (эпюры Qy i(xi), Qz i(xi) показаны на эпюре Q; эпюры My i(xi), Mz i(xi) совмещены и показаны на эпюре М).
| Эп. N (кН) | Эп. Q (кН) |
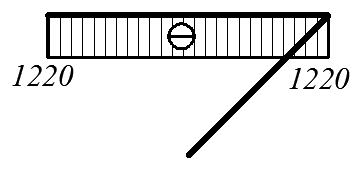
| 
|
| Эп. М (кН·м) | Эп. Mt (кН·м) |
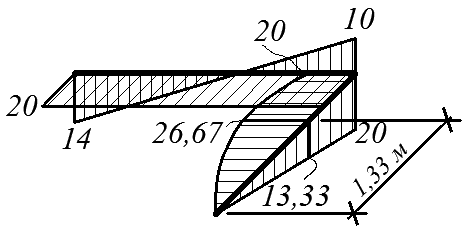
| 
|
Рис. 4.32
2. Определение формы сопротивления стержня на участках
Участок ① – стержень подвергается косому изгибу.
Участок ② – стержень испытывает общий случай сложного сопротивления (косой изгиб с кручением и осевым сжатием).
3. Подбор сечений стержня на участках
Участок ① – стержень подвергается косому изгибу.
Сечения, подозреваемые на опасные:
x1 = 1,33 м, My1 = 26,67 кН·м, Mz1 = 13,33 кН·м;
x2 = 2 м, My1 = 20 кН·м, Mz1 = 20 кН·м.
Для сечения с координатой x1 = 1,33 м My1 > Mz1. Поэтому рациональной ориентацией главных центральных осей инерции сечения типа «а» на участке ① будет такая, при которой ось, относительно которой момент сопротивления сечения максимален, параллельна оси y1. Определим моменты инерции и моменты сопротивления сечения типа «а» относительно осей 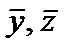 .
.