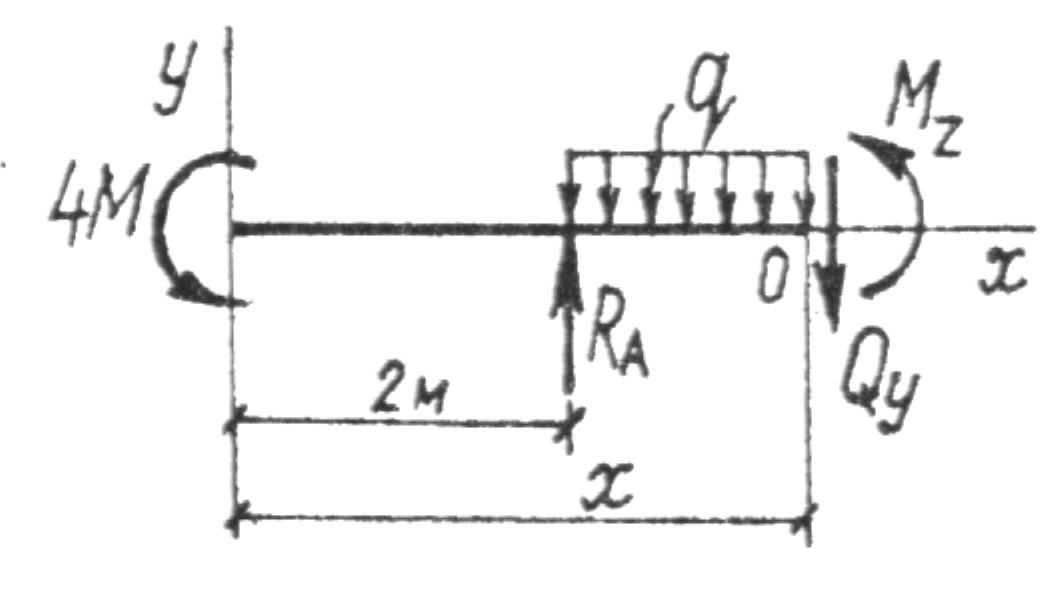
Расчет балки на прочность

Дата: 2025-05-25; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Определение реакций опор

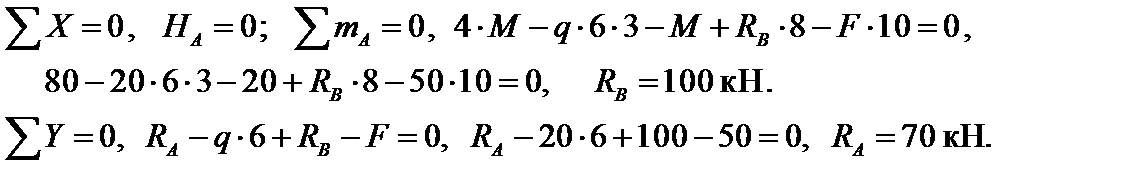
Проверка:

Sm_B = 0; 80 – 70 · 8 + 20 · 6 · 5 – 20 – 50 · 2 = 0; 0 = 0.

(Верно)

Построение эпюр Q_y, M_z

Балка имеет четыре грузовых участка.

1-й грузовой участок: 0 ≤ х ≤ 2 м.

SY = 0 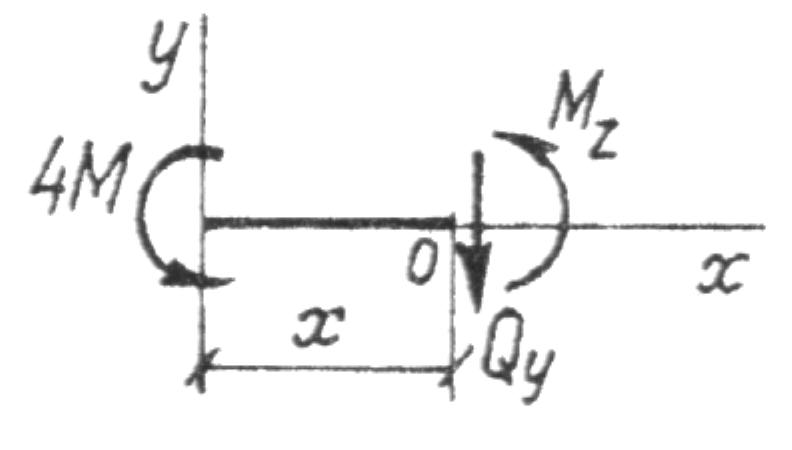, Q_y = 0;

Sm_O = 0, 4 · M + M_z = 0,

M_z = –4 · M = –80 кН·м.

2-й грузовой участок: 2 м ≤ х ≤ 8 м.

SY = 0,

R_A – q · (x – 2) – Q_y = 0,

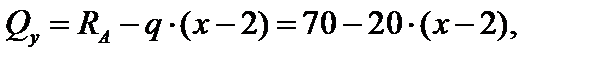
х = 2 м, Q_y = 70 кН;

х = 8 м, Q_y = – 50 кН

(так как Q_y на участке меняет знак, то M_z имеет экстремум).

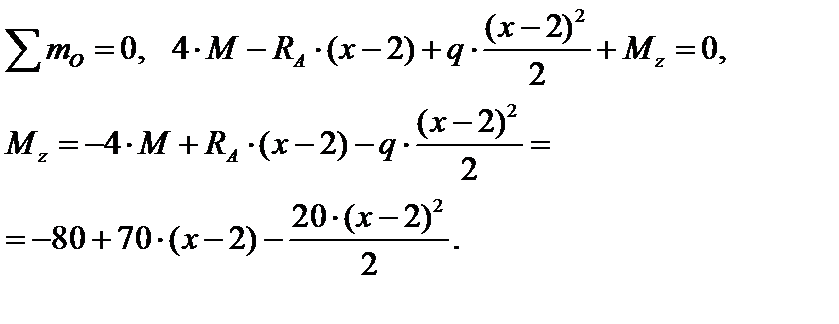
Найдем положение экстремума:

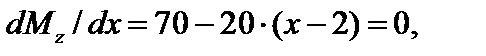x = 5,5 м,

х = 2 м, M_z = –80 кН×м;

х = 5,5 м, M_z = 42,5 кН×м;

х = 8 м, M_z = –20 кН×м.

Для грузовых участков 3 и 4 вычисление M_z и Q_y выполнять аналогично, рассматривая правую отсеченную часть балки.

Эпюры Q_y и M_z показаны на рис. 4.22.

Определение положения опасных сечений

· 1-е опасное сечение: кН×м;

· 2-е опасное сечение: кН;

· 3-е опасное сечение: M_z = – 100 кН×м; Q_y = 50 кH.

Определение размеров поперечных сечений балки

Из условия прочности по нормальным напряжениям в опасных точках D (рис. 4.23, 4.24) 1-го опасного сечения определим требуемый момент сопротивления:

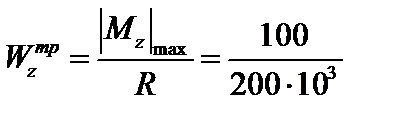= 0,5·10^–3 м³ = 500 см³, 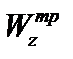= 500 см³.

Поперечное сечение варианта (а) (см. рис. 4.23) состоит из двух швеллеров. Для одного швеллера W_z = 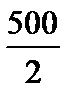= 250 см³.

По ГОСТ 8240-89 находим:

[ № 24, W_z = 242 см³;

2 [ № 24, W_z = 484 см³.

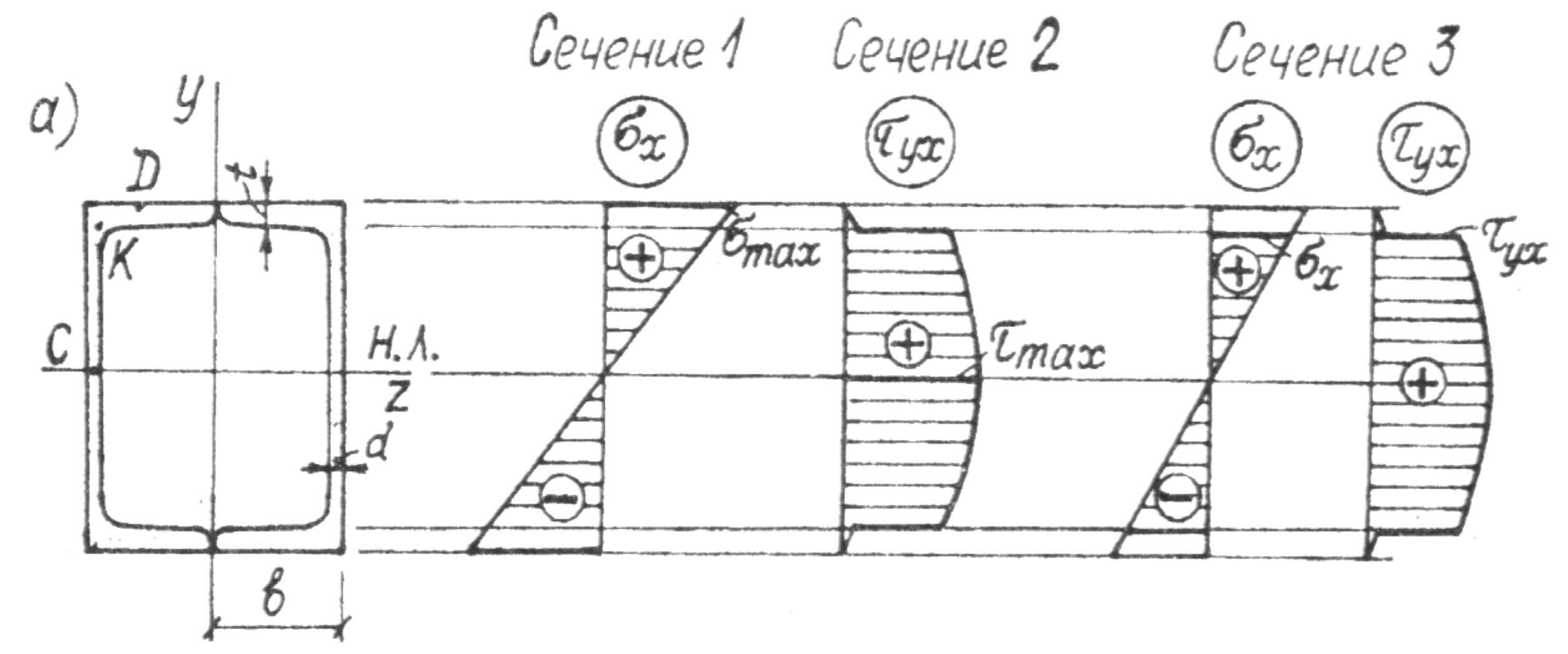
Рис. 4.23

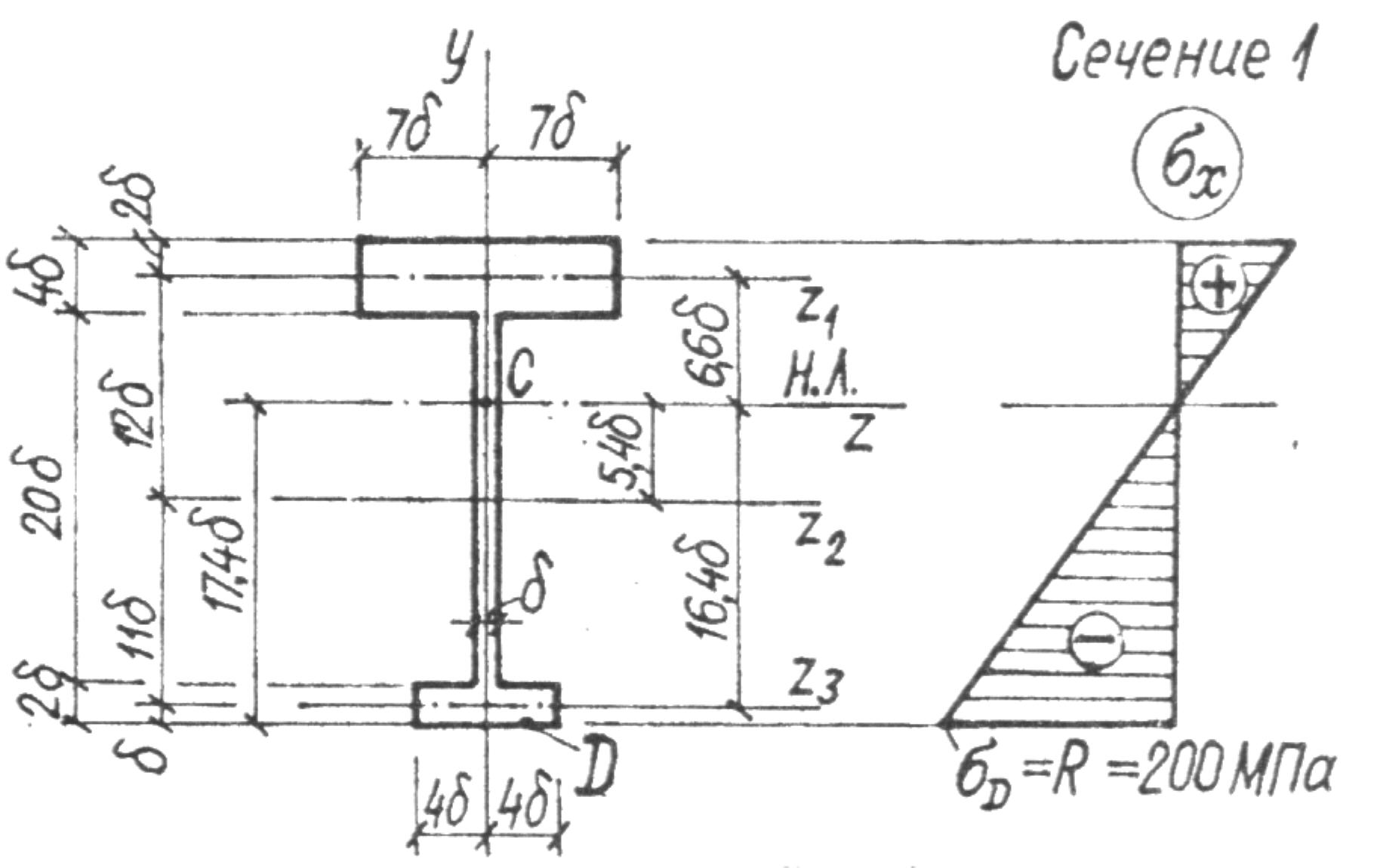
Рис. 4.24

Проверяем прочность принятого сечения по нормальным напряжениям:

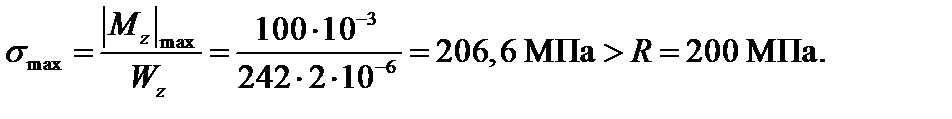
Перенапряжение

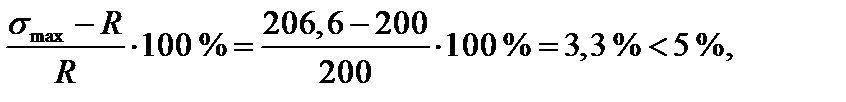
что допустимо.

Проверка прочности по касательным напряжениям в опасной точке С (см. рис. 3.4) 2-го опасного сечения (чистый сдвиг):

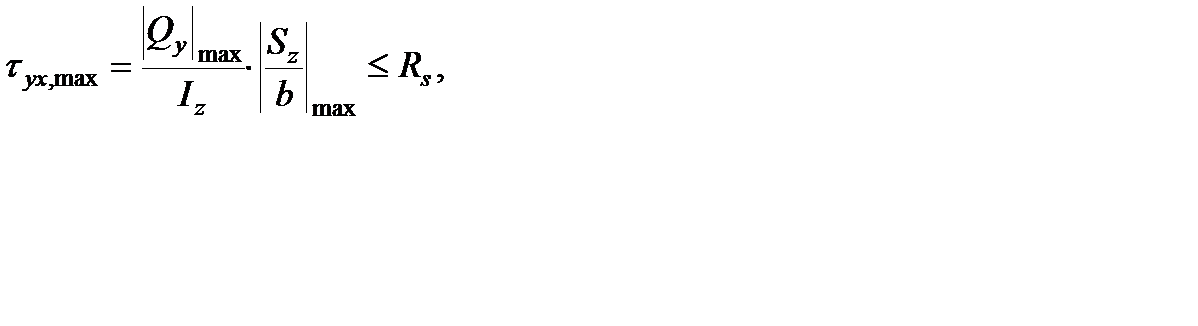
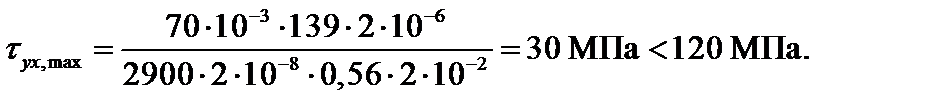
Значение S_z для точки С, расположенной на нейтральной оси, берем из того же ГОСТ 8240-89.

Проверка прочности в опасной точке K (см. рис. 4.23) 3-го опасного сечения, где имеет место плоское напряженное состояние:

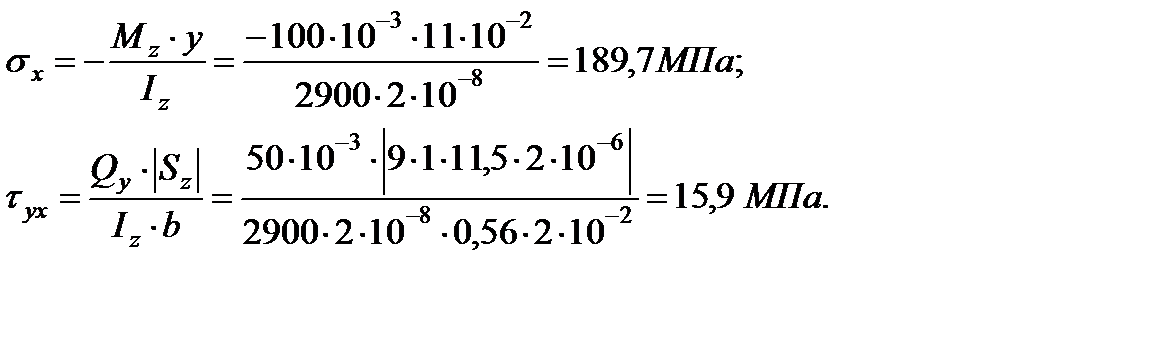189,7 МПа;

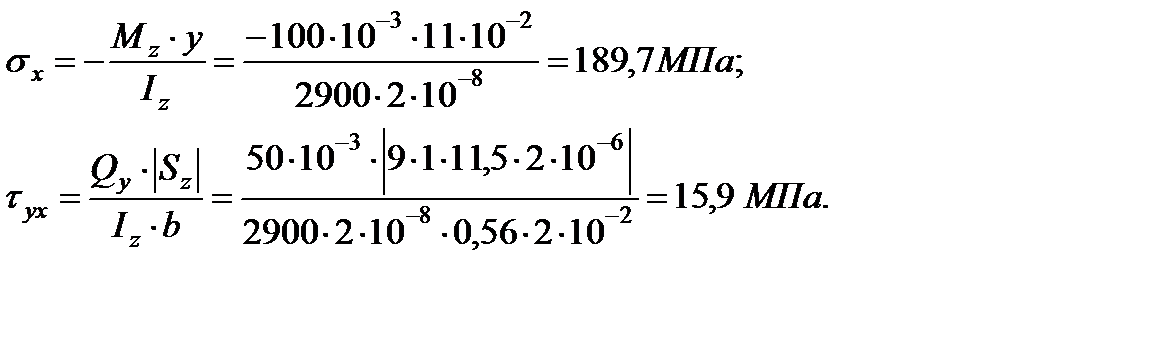15,9 МПа.

По гипотезе прочности наибольших касательных напряжений имеем: . Для балки при прямом поперечном изгибе получим:

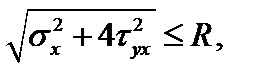
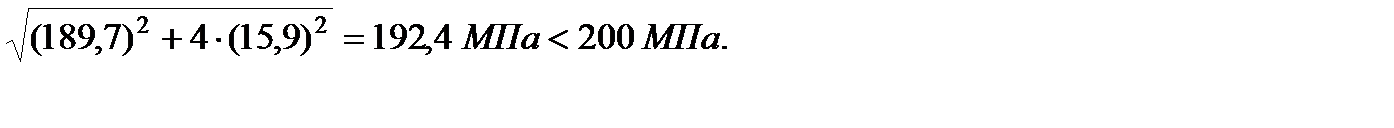192,4 МПа < 200 МПа.

По энергетической гипотезе прочности имеем:

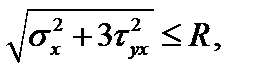
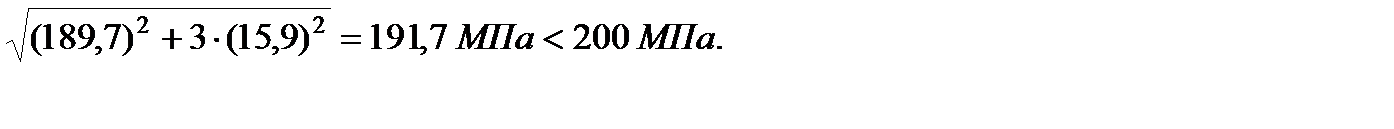191,7 МПа < 200 МПа.

Следовательно, прочность материала балки во всех точках обеспечена.

Рассмотрим расчет сварной балки – вариант (б) с поперечным сечением, показанным на рис. 4.24.

Определим положение центра тяжести сечения:

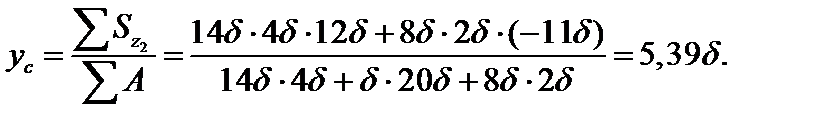
Вычислим момент инерции:

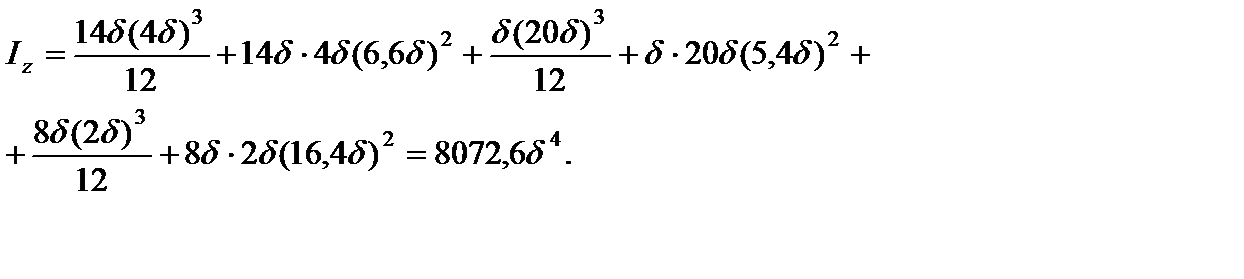
Момент сопротивления

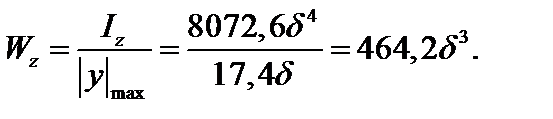
Из условия прочности по нормальным напряжениям в опасной точке D (см. рис. 4.24) 1-го опасного сечения требуемый момент сопротивления равен

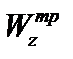= 464,2d ³ = 500.

Отсюда .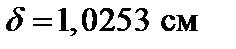

В соответствии с найденной величиной 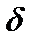принимаем размеры поперечного сечения с округлением до 1 мм (см. рис. 4.24). Пересчитав характеристики сечения, получим: I_z = 9017,6 см⁴, W_z = 503,8 см³. Напряжение s_max = 198,5 МПа < R = 200 МПа.

Проверка прочности по касательным напряжениям в опасной точке С (рис. 4.25) 2-го опасного сечения:

;

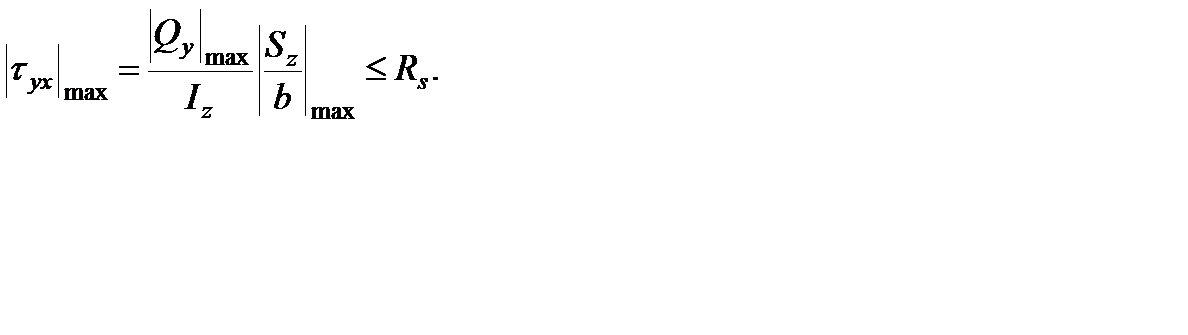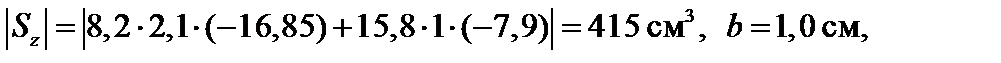
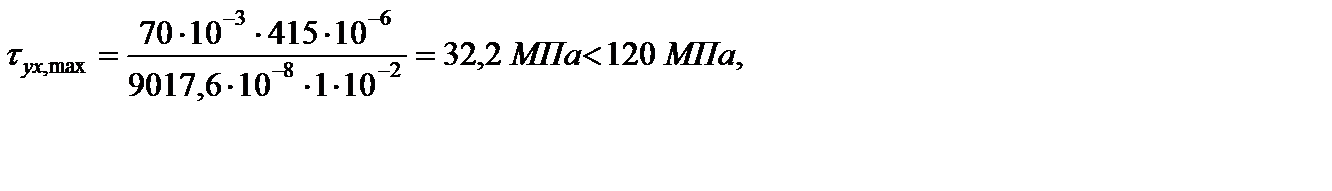32,2 МПа < 120 МПа,

т.е. условие прочности в точке С выполнено.

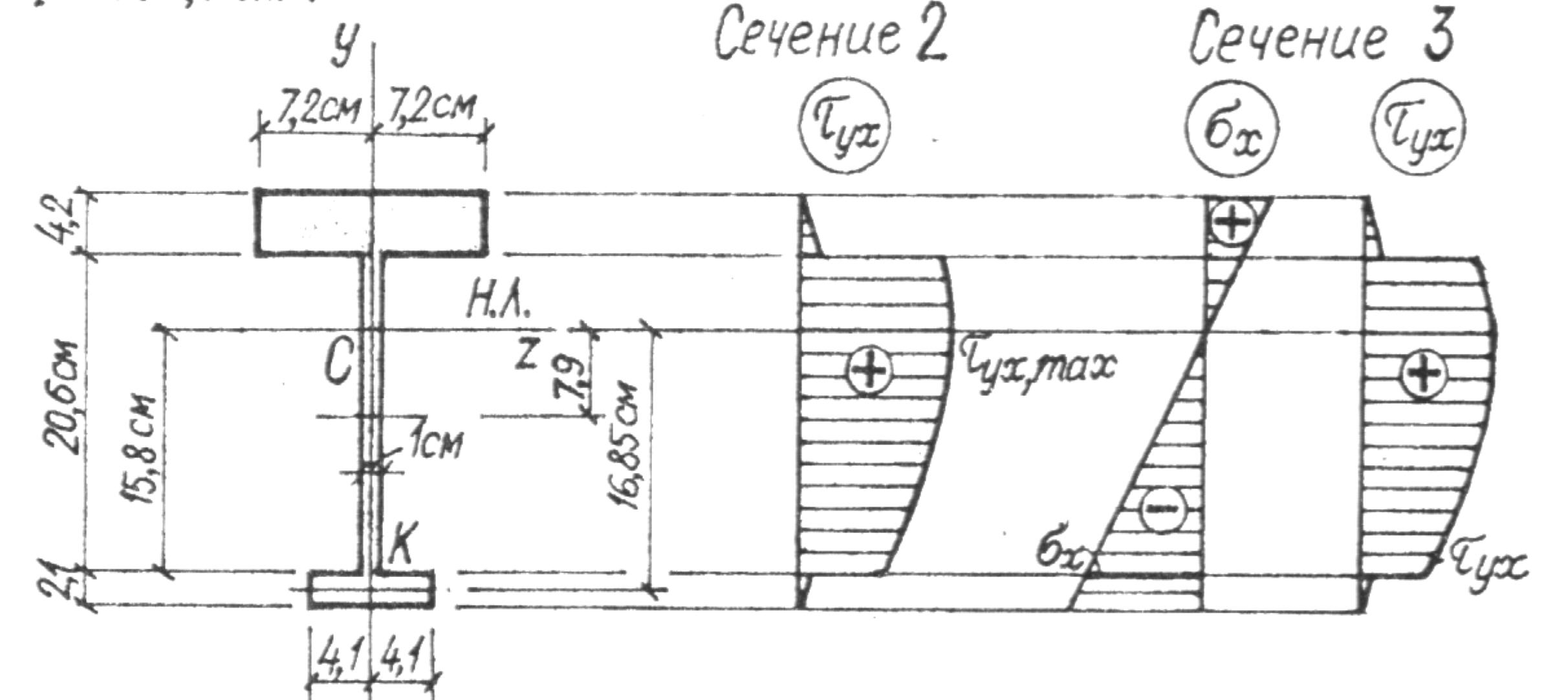
Рис. 4.25

Проверка прочности в опасной точке K (см. рис. 4.25) 3-го опасного сечения, где имеет место плоское напряженное состояние:

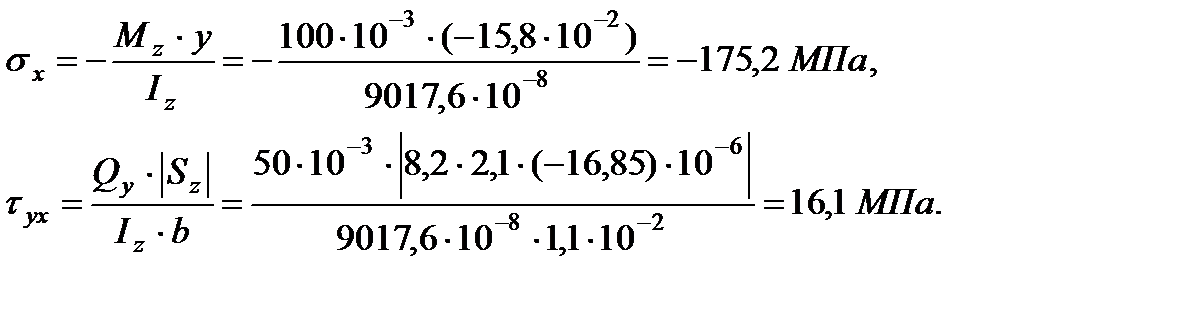
= –175,2 МПа,

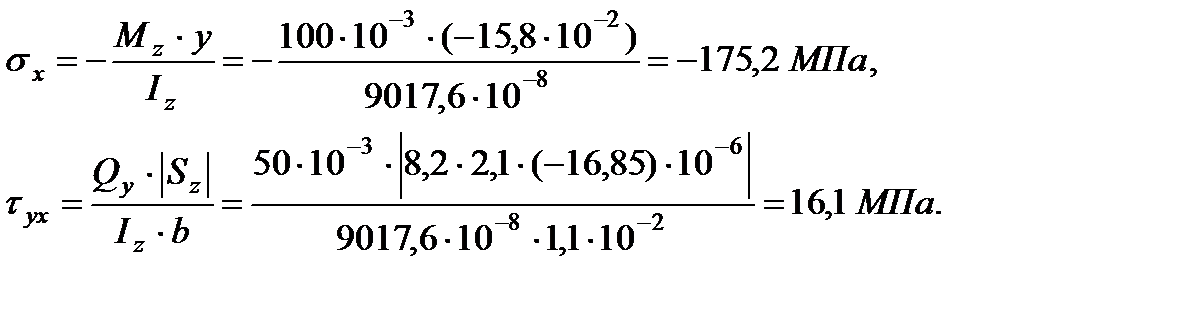16,1 МПа.

По гипотезе прочности наибольших касательных напряжений имеем:

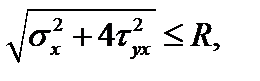
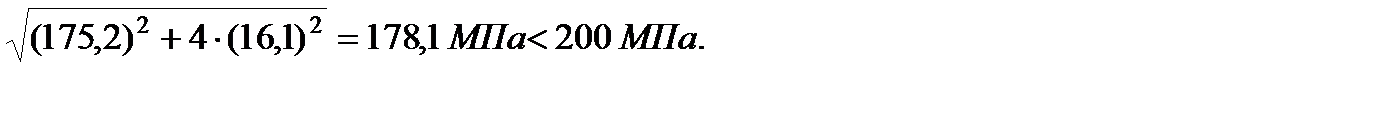178,1 МПа < 200 МПа.

По энергетической теории прочности получим:

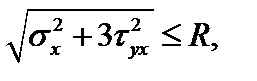
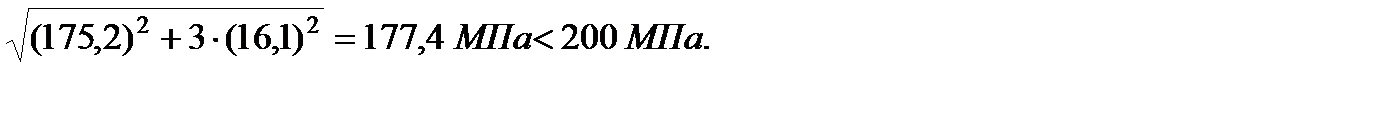177,4 МПа < 200 МПа.

Условие прочности в точке K выполнено.

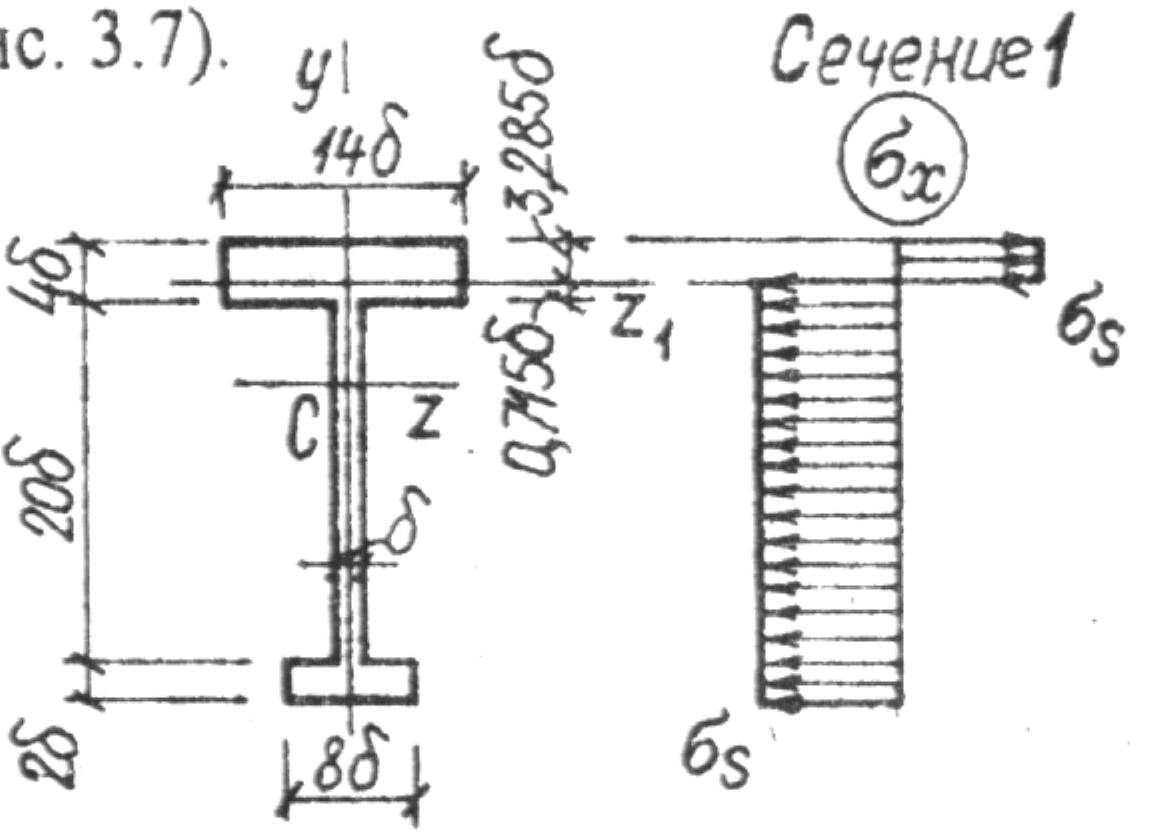
Расчет по предельной несущей способности (поперечное сечение приведено на рис. 4.26).

Дано: = 240 МПа, k = 1,2.

Определить размер .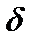

Площадь поперечного сечения равна

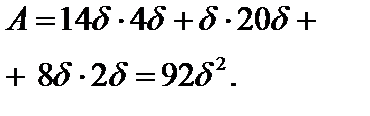
Нейтральная ось z₁ не проходит через центр тяжести сечения и делит площадь поперечного сечения А на две равновеликие

площади:

Предельный момент в пластическом шарнире имеет выражение

M_lim = s _s·W_s.

Пластический момент сопротивления

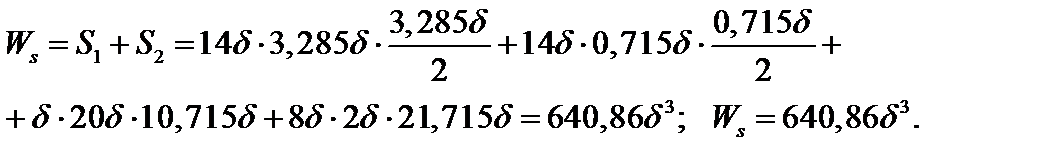
Из условия прочности по предельной нагрузке

d³ = 0,780 см³; d = 0,920 см.

Сопоставив результаты расчетов методами расчетного сопротивления (d = 1,025 см) и предельной несущей способности (d = 0,920 см), увидим, что более экономичное сечение получается при расчете методом предельного равновесия.