Геометрическая сторона задачи. Так как опоры 0, 3 – недеформируемые, то углы закручивания начального сечения 0 и конечного 3 равны нулю, т.е.

Дата: 2025-05-25; Просмотры: 4

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

при х = 0 j₁(0) = j₀ = 0; (а)

при х = 3 j₃(3) = 0. (б)

Условия (а), (б) характеризуют геометрическую сторону данной задачи.

Физическая сторона задачи. Будем полагать, что при деформировании стержня справедлив закон Гука (линейно-упругое деформирование). Тогда, используя выражение (3.26) для функции углов закручивания сечения на участке, а также условия (а), (б), получим:

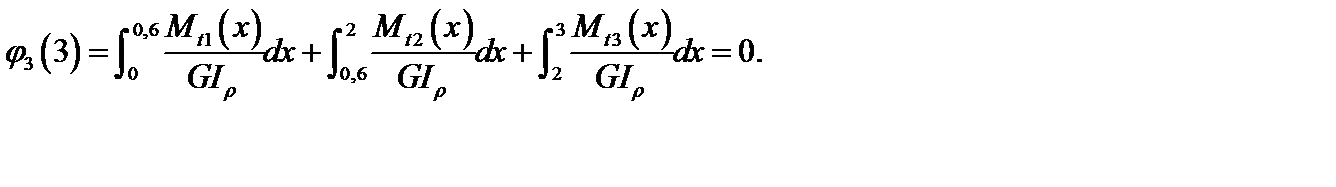(2)

Выделяя левые (по отношению к текущему сечению) части стержня, найдем выражения для крутящих моментов в сечениях на участках:

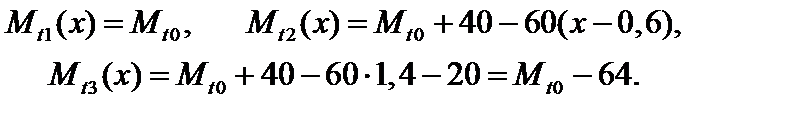(в)

Подставляя (в) в (2), после сокращения 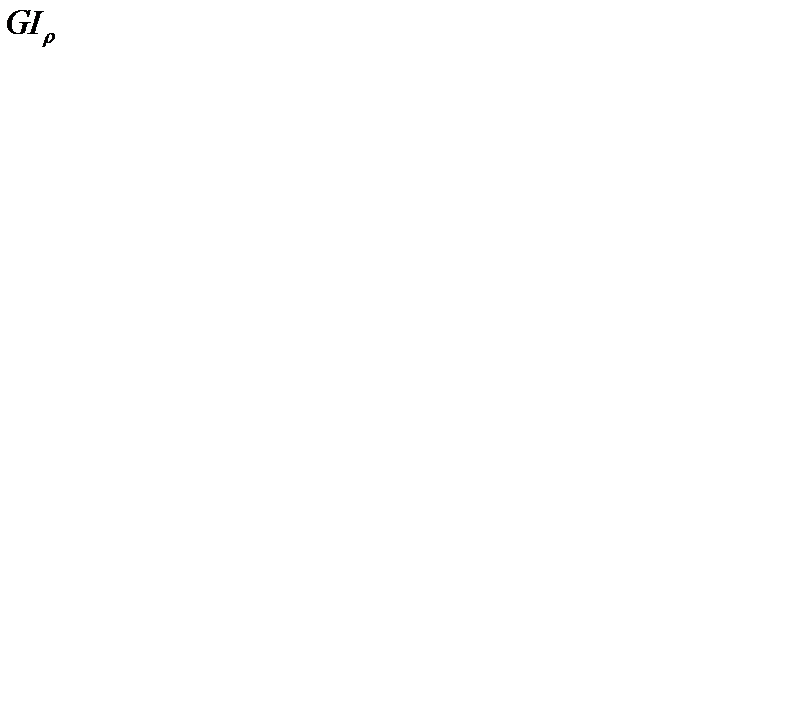и интегрирования получим: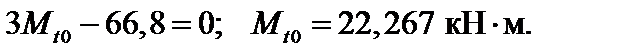

2. Подбор круглого поперечного сечения стержня из условия расчета по несущей способности

Условие прочности стержня при расчете по несущей способности (расчетному сопротивлению) имеет вид:

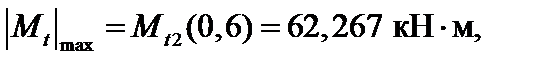
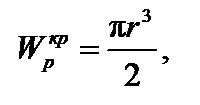
Учитывая, что кН/м² получим условие

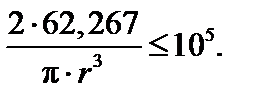
Отсюда

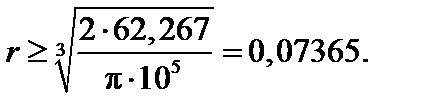
Площадь поперечного сечения равна

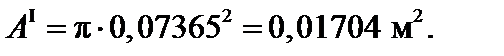
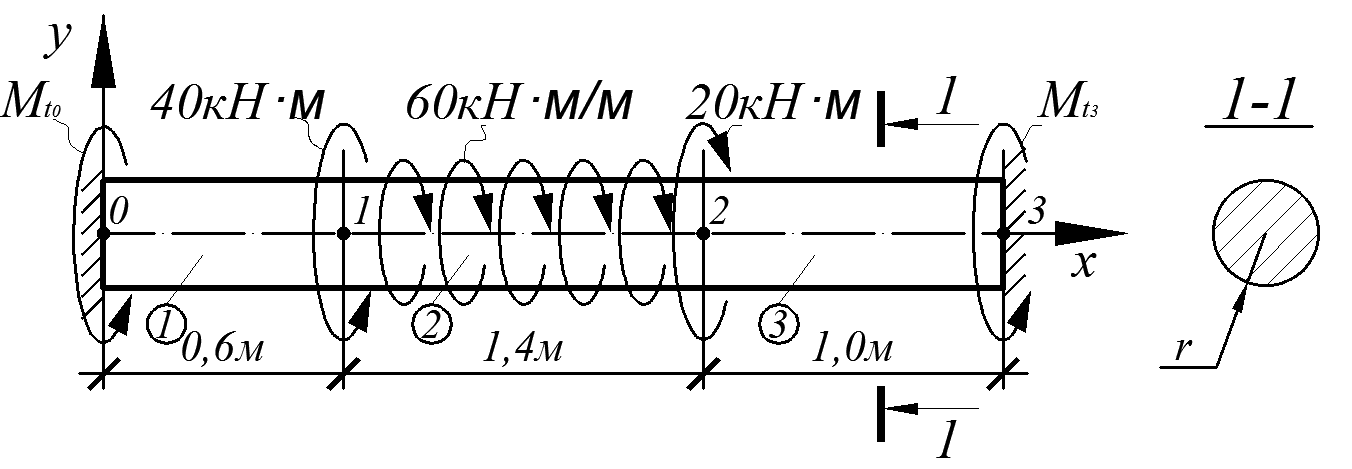
Эп. M_t(x), кН·м

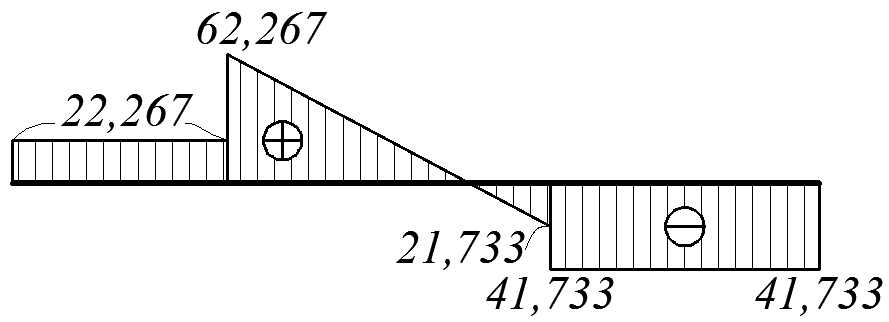
Рис. 4.20

3. Подбор круглого поперечного сечения стержня из условия расчета по предельной нагрузке

Выразим нагрузку на стержень через один параметр – интенсивность распределенного закрученного закручивающего момента m = 60 кН·м/м. Тогда

Предельный крутящий момент для круглого сечения равен

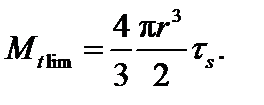
Увеличивая параметр нагрузки до предельного значения m_lim, придем к предельному состоянию стержня, характеризующемуся следующей эпюрой (рис. 4.21).

Эп. (в предельном состоянии)

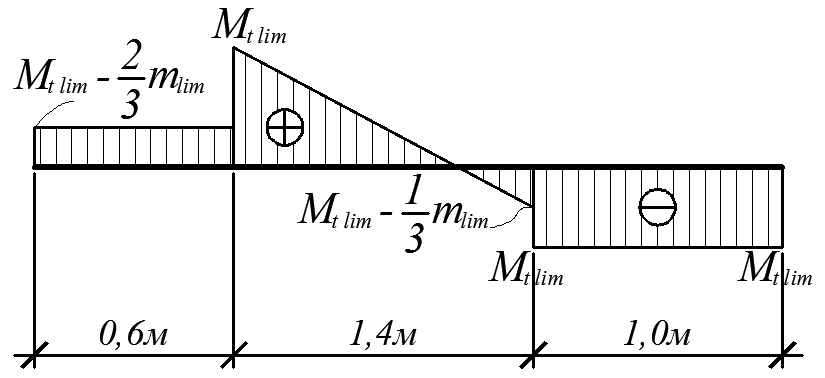
Рис. 4.21

Анализируя полученную эпюру , придем к уравнению для определения m_lim:

M_{t lim} – 1,4m_lim = –(M_{t lim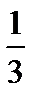} – m_lim). (3)

Отсюда

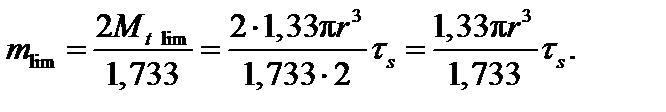
Условие расчета по предельной нагрузке имеет вид:

.

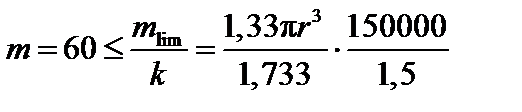Отсюда

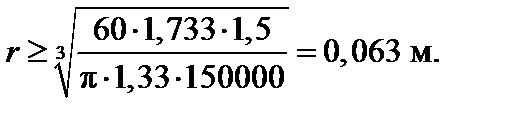
Площадь полученного сечения равна

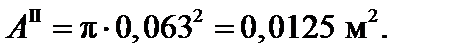
4. Сравнение результатов расчетов по расчетному сопротивлению (несущей способности) и по предельной нагрузке

Определим величину

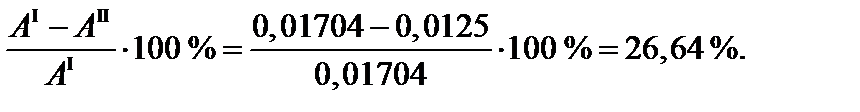
Таким образом, при расчете по предельной нагрузке экономия материала составила в данном случае 26,64 % по сравнению с проектом, найденным из условия расчета по несущей способности (расчетному сопротивлению). При этом коэффициенты запаса прочности были одинаковы и равнялись 1,5.

4.3.3. Контрольные вопросы для самопроверки

1. При каком нагружении прямой стержень испытывает только деформацию кручения?

2. Какие напряжения возникают в поперечном сечении стержня при деформации кручения и как они определяются?

3. Как распределяются касательные напряжения в круглом и круглом кольцевом поперечных сечениях стержня при кручении?

4. Как распределяются касательные напряжения в прямоугольном поперечном сечении стержня при кручении?

5. Как записывается условие расчета по несущей способности (условие прочности) для стержня круглого или кольцевого сечения при кручении?

6. Как записывается условие расчета по несущей способности (условие прочности) для стержня прямоугольного сечения при кручении?

7. Как записывается условие расчета по предельной нагрузке для стержня круглого сечения?

8. Какие перемещения поперечных сечений определяются при кручении?

9. Как записывается условие жесткости при кручении прямых стержней?

10. Каков порядок расчета статически неопределимых систем при кручении?

4.4. Прямой поперечный изгиб балок

4.4.1. Задача 4.1

Требуется из расчета на прочность определить размеры поперечного сечения балки (рис. 4.22) в двух вариантах: (а) и (б) (см. рис. 3.12), а затем проверить балку, имеющую поперечное сечение (а), на жесткость.

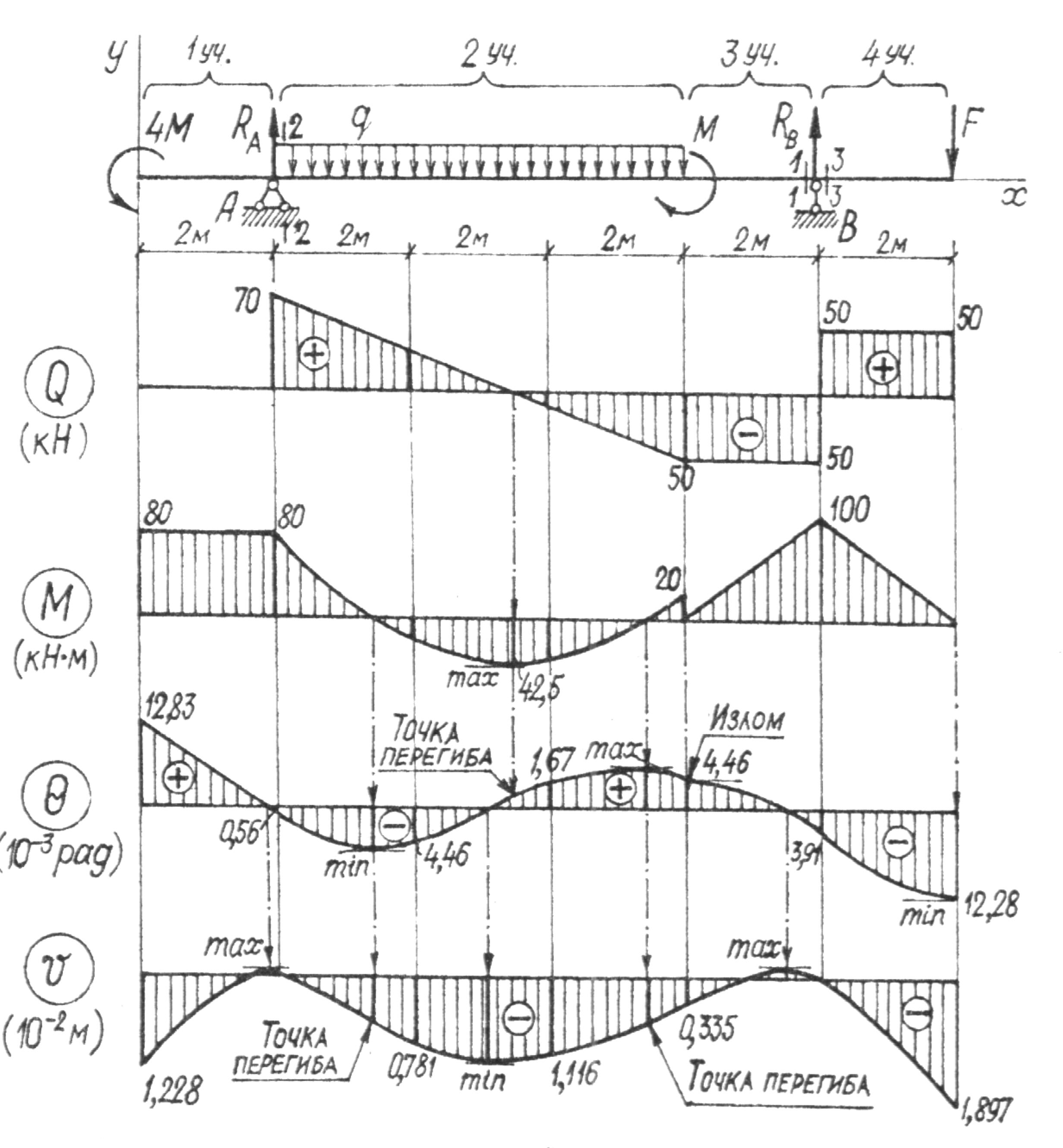
Рис. 4.22

Принять: М = 20 кН×м, q = 20 кН/м, F = 50 кН, R = 200 МПа, R_s = 120 МПа, б _s = 240 МПа, k = 1,2 (коэффициент запаса прочности).