4.2.4. Контрольные вопросы для самопроверки
1. Что называют напряженно-деформированным состоянием в точке?
2. Какие напряжения называют главными?
3. Какие напряженные состояния называют линейным, плоским и объемным?
4. Как обозначают главные напряжения?
5. Сформулируйте закон парности касательных напряжений.
6. Какое напряженное состояние называют чистым сдвигом?
7. Как записать обобщенный закон Гука?
8. Какие деформации называются главными и как их определить?
9. Что называется гипотезами прочности?
10. Сформулируйте основные теории прочности.
11. Что называют статическим моментом сечения?
12. Может ли статический момент быть отрицательным или равным нулю?
13. Какие оси называют центральными?
14. Чему равны статические моменты относительно центральных осей?
15. Что называют осевым моментом инерции сечения?
16. Может ли осевой момент инерции быть отрицательным или равным нулю?
17. Что называют центробежным моментом инерции сечения?
18. Может ли центробежный момент инерции быть отрицательным или равным нулю?
19. Чему равен центробежный момент инерции относительно осей, одна из которых является осью симметрии сечения?
20. Какова размерность моментов инерции?
21. Какие оси называют главными осями?
22. Какие оси называют главными центральными осями?
23. Как определить положение главных центральных осей, если известны моменты инерции относительно некоторых двух взаимно перпендикулярных осей?
24. Каким свойством обладают моменты инерции относительно главных центральных осей?
25. Что называется радиусом инерции сечения?
4.3. Расчет прямых стержней при деформации кручения
4.3.1. Задача 3.1
Для стержня, изображенного на рис. 4.16, требуется:
1. Построить эпюру Mt от заданной расчетной нагрузки.
2. Подобрать поперечное сечение стержня в трех вариантах (см. рис. 3.11) из условия прочности.
3. Построить эпюру углов закручивания сечения при постоянной жесткости стержня, т.е. 
4. Подобрать кольцевое сечение стержня из условия жесткости, считая нормативную нагрузку равной расчетной.
5. Выбрать кольцевое сечение стержня из условий прочности и жесткости.
Исходные данные:
Rs = 100 МПа, G = 0,8·105 МПа, D = 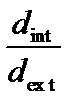 = 0,9,
= 0,9,
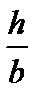 = 2, [j] = 0,01 рад.
= 2, [j] = 0,01 рад.
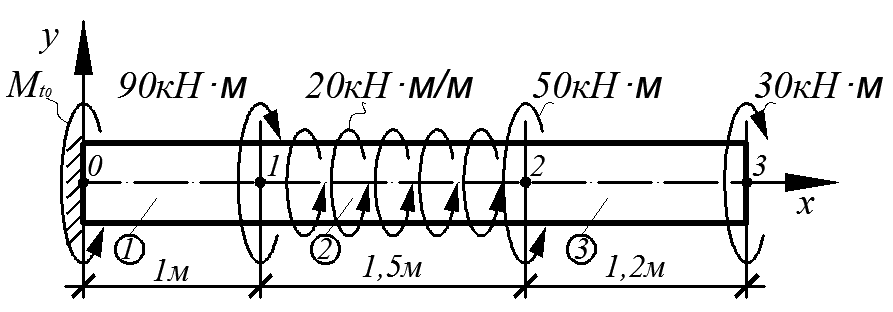
Рис. 4.16
Решение
1. Определение опорной реакции Mt0
Составляем уравнение равновесия стержня:
Smx = Mt0 – 90 + 20·1,5 + 50 – 30 = 0. (1)
Из (1) получим: 
2. Построение эпюры крутящих моментов в сечениях
Разобьем стержень на 3 участка: ①, ②, ③ (см. рис. 4.16). Выбирая произвольное сечение на участке i, отсекая какую-либо часть стержня (например, левее выбранного стержня), составляем далее уравнение равновесия остальной части стержня. Из полученного уравнения находим выражения Mti(x).
Участок ①: 0 ≤ х ≤ 1 м, 1 м ≤ х ≤ 2,5 м
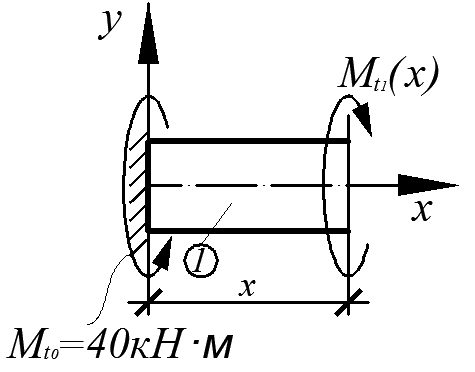
| Smx = 40 – Mt1(х) = 0, Mt1(х) = const = 40 кН·м. (а) |
Участок ②: 1 м ≤ х ≤ 2,5 м
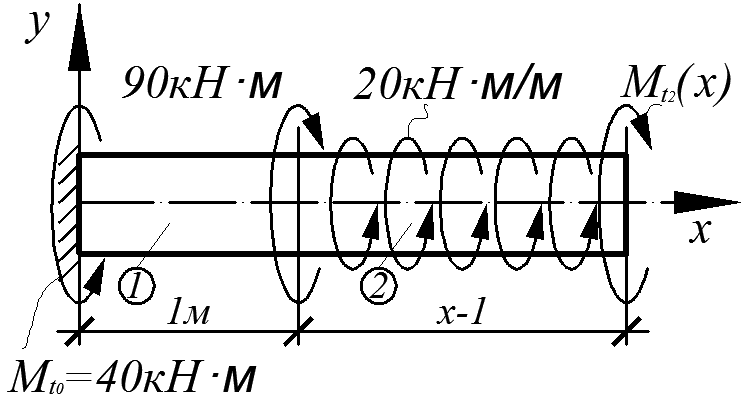
| Smx = 40 – 90 + 20(х–1)–Mt2(х) = 0. Mt2(х) = –50 + 20(х–1) кН·м. (б) |
Аналитически находим Mt3(х) = const = 30 кН·м (в)
Используя полученные выражения (а), (б), (в), строим эпюру Mt (рис. 4.17).

Эп. Mt(х), кН·м
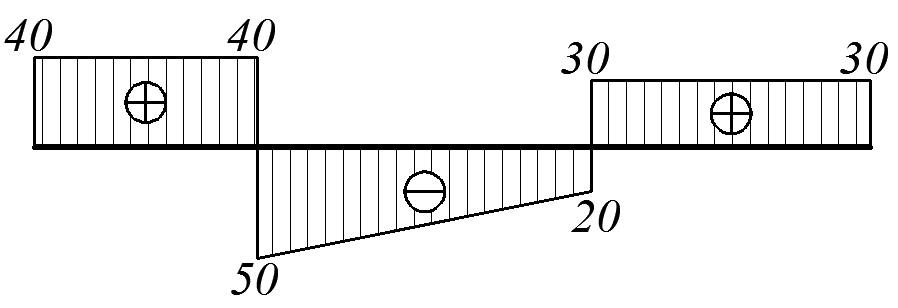
Рис. 4.17
3. Подбор сечений (в трех вариантах) из условия прочности
Так как стержень выполнен из одного материала и имеет постоянное сечение, условие прочности записывается в виде:
 (2)
(2)
Анализируя эпюру Mt, находим  Рассмотрим различные варианты сечений стержня (рис. 3.11).
Рассмотрим различные варианты сечений стержня (рис. 3.11).
А. Круглое сечение
Условие (2) имеет вид:
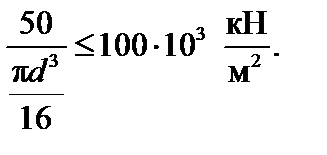
Отсюда получим: 
Акруг = 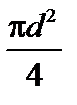 = 0,01467 м2.
= 0,01467 м2.
Б. Кольцевое сечение
Условие (2) имеет вид:
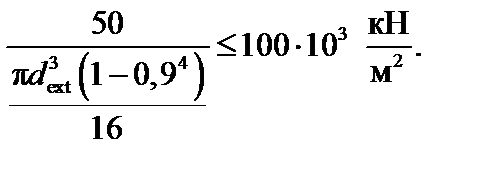
Отсюда получим 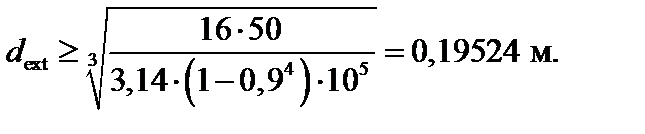
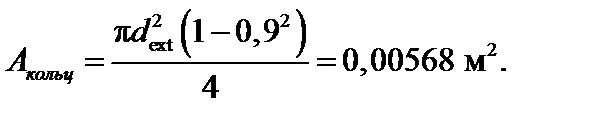
В. Прямоугольное сечение
Условие (2) имеет вид:
 Согласно исходным данным
Согласно исходным данным 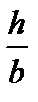 = 2.
= 2.
По табл. П.2 принимаем a = 0,246.
Записываем условие прочности в виде:

Отсюда получим
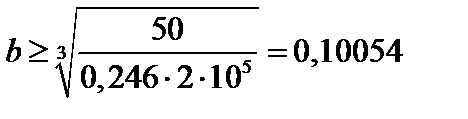 м. Акв = 2b2 = 0,0202 м2.
м. Акв = 2b2 = 0,0202 м2.
Таким образом, наиболее предпочтительным при кручении является кольцевое сечение.
4. Построение эпюры углов закручивания сечений при постоянной жесткости стержня GIp = const
Будем полагать, что нормативная нагрузка совпадает с расчетной. Тогда при определении  на участках ①, ②, ③ можно использовать полученные соотношения (а), (б), (в) для
на участках ①, ②, ③ можно использовать полученные соотношения (а), (б), (в) для  При выбранной системе координат
При выбранной системе координат  Тогда
Тогда
 (г)
(г)
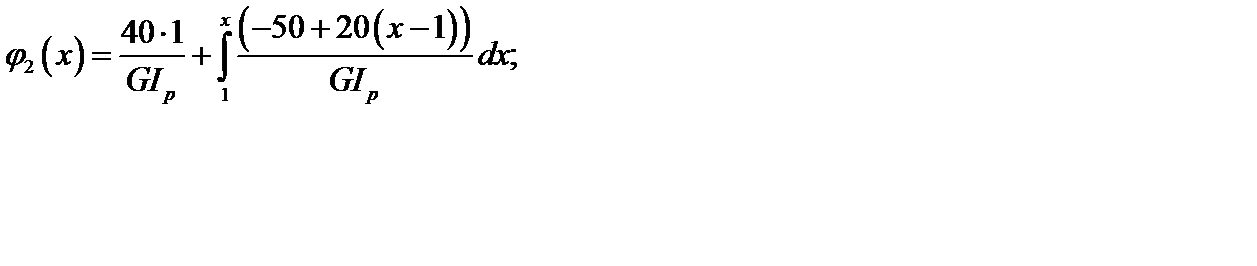
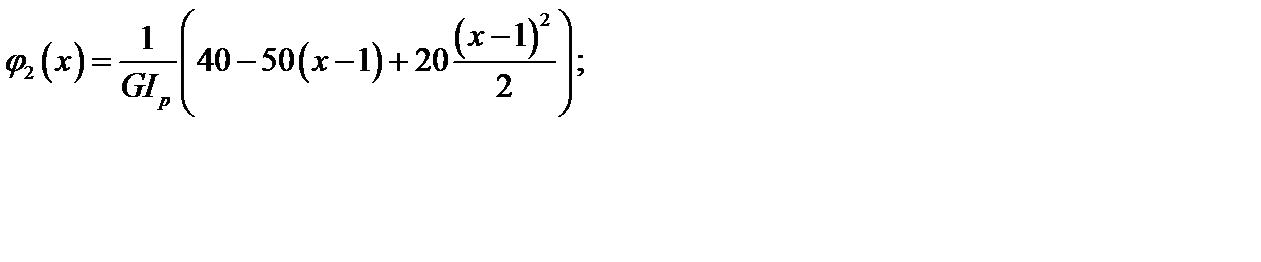 (д)
(д)
j3(x) = 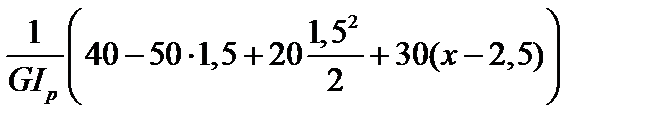 . (е)
. (е)
Учитывая полученные соотношения (г), (д), (е), строим эпюру углов закручивания сечений (рис. 4.18).
Эп. j
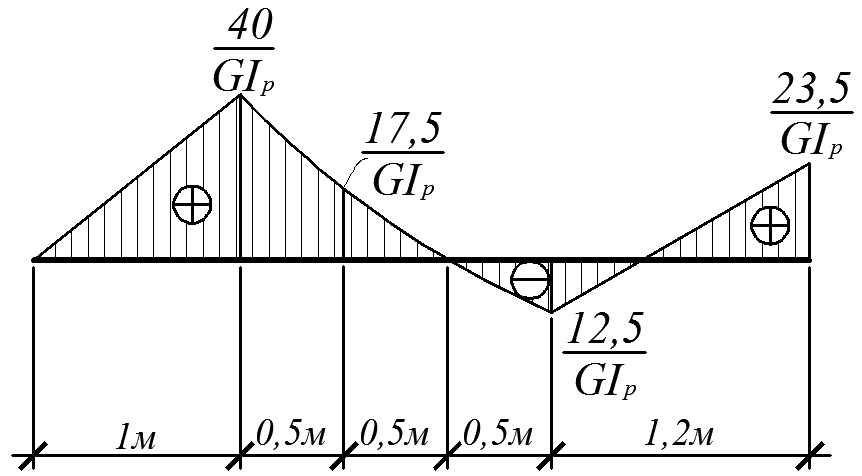
Рис. 4.18
5. Подбор кольцевого сечения из условия жесткости
Условие жесткости (3.25) в данном случае имеет вид:

Учитывая, что G = 0,8·105 МПа,
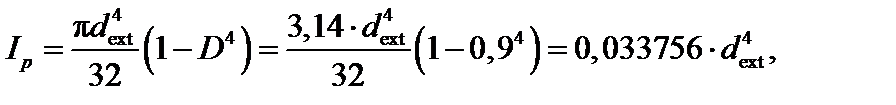
получим

Сравнивая величины dext, полученные при расчете на прочность и жесткость, принимаем окончательно dext ≥ 0,19618 м.
Таким образом, в данном случае размер кольцевого сечения необходимо принимать из условия жесткости.
4.3.2. Задача 3.2
Для стержня, расчетная схема которого изображена на рис. 4.19, требуется:
1. Построить эпюру Mt в предположении линейно-упругой работы материала.
2. По условию прочности (расчет по несущей способности) подобрать круглое поперечное сечение стержня.
3. Подобрать круглое поперечное сечение стержня из условия расчета по предельной нагрузке.
4. Сравнить результаты расчетов по расчетному сопротивлению (несущей способности) и по предельной нагрузке.
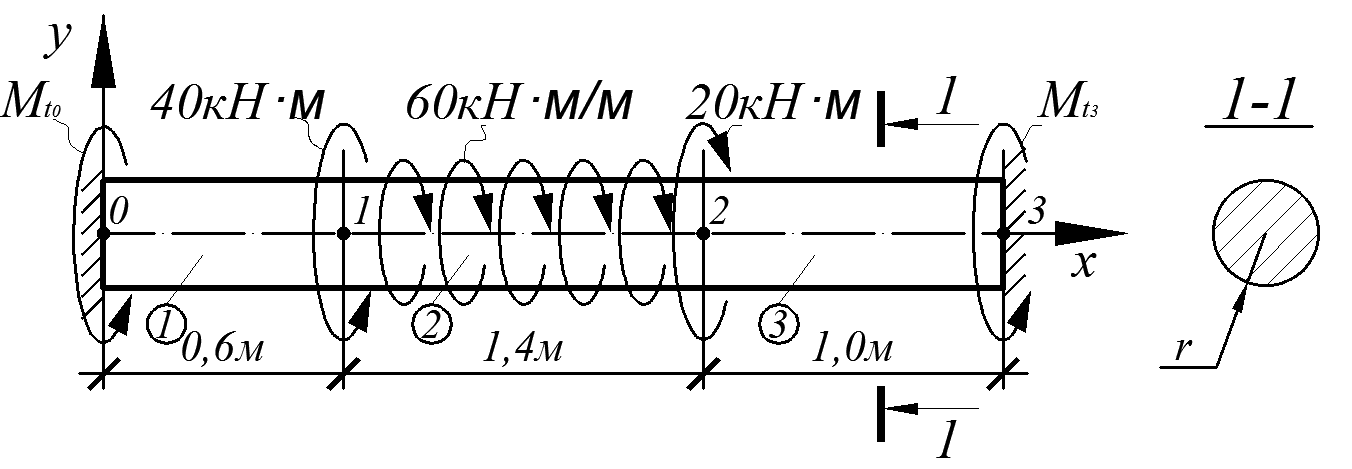
Рис. 4.19
Исходные данные: расчетное сопротивление материала при сдвиге Rs = 100 МПа, предел текучести при сдвиге 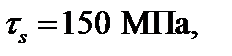 коэффициент запаса прочности по нагрузке
коэффициент запаса прочности по нагрузке 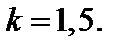
Решение
1. Построение эпюры Mt в предположении линейно-упругой работы материала
Система, изображенная на рис. 4.19, один раз статически неопределима. Для раскрытия статической неопределимости (определения реакции Mt0, Mt3) необходимо рассмотреть три стороны задачи.
Статическая сторона задачи. Отсекая стержень от опор, оставим уравнение равновесия всего стержня:
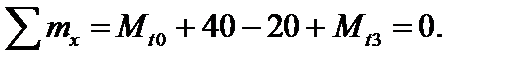 (1)
(1)








