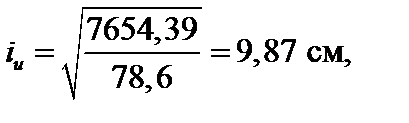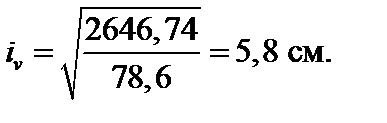2. Определить величины главных центральных моментов инерции.

Дата: 2025-05-25; Просмотры: 6
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

3. Определить величины главных центральных радиусов инерции сечения.

Разбиваем сечения на простые фигуры и проводим их центральные оси 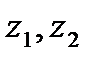и y. Ось симметрии y является главной центральной осью данного сечения (рис. 4.13).

Для определения положения второй главной центральной оси выбираем произвольную ось z¢, перпендикулярную оси симметрии.

Определяем ординату y ¢ c центра тяжести поперечного сечения по оси y по формуле (3.17):

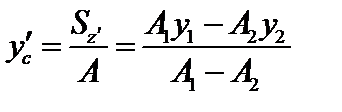, A1 = 28·24 = 672 см2, A2 = 16·12 = 192 см2 ;

A = A1 – A2 = 480 см2; y1 = 12 см, y2 = 6 см;

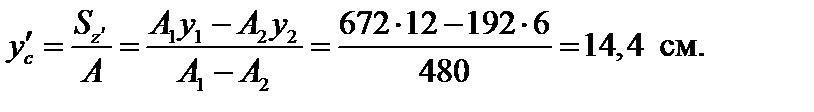
Откладываем размер yc вверх от оси z¢ и проводим вторую главную центральную ось z (см. рис. 4.13).

Определяем осевые моменты инерции простых фигур относительно собственных центральных осей:

 

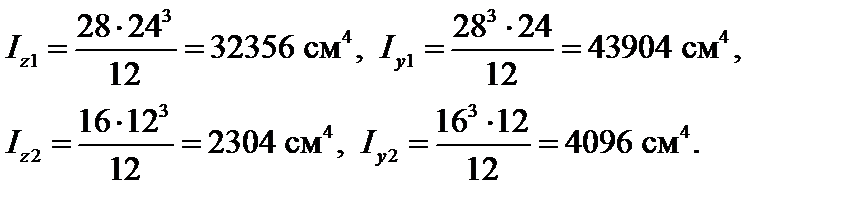
Вычисляем расстояние от центральных осей всего сечения z и y до центральных осей отдельных фигур (рис. 4.13):

 

 

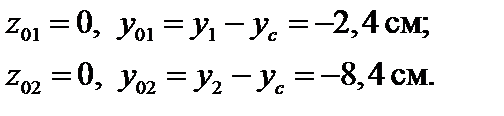
Главные центральные моменты инерции вычисляются с использованием (3.18):

 

Iz = (32356 + 672·2,42) – (2304 + 192·8,42) = 20375,2 см4;

Iy = (43904 + 672·0) – (4096 + 192·0) = 39808 см4.

 

Центробежный момент инерции Izy всего сечения равен нулю, т.к. ось y является осью симметрии, т.е. оси z и y являются главными центральными осями инерции сечения, а вычисленные осевые моменты инерции – главными центральными моментами инерции:

Imin = Iz = 20375,2 см4, Imax = Iy = 39808 см4.

 

Значения главных центральных радиусов инерции сечения:

 

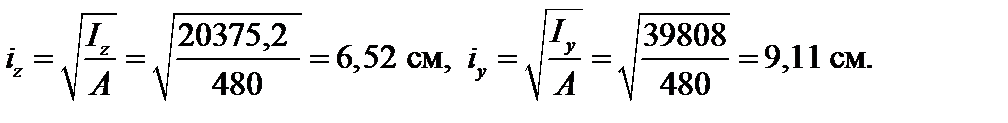
4.2.3. Задача 2.3

Для заданного поперечного сечения (рис. 4.14) требуется:

1. Определить координаты центра тяжести сечения и провести горизонтальную и вертикальную центральные оси.

2. Определить осевые и центробежный моменты инерции сечения относительно проведенных центральных осей.

3. Определить положение главных центральных осей инерции и показать их на чертеже.

4. Вычислить величины главных центральных моментов инерции.

5. Определить величины главных центральных радиусов инер­ции сечения.

Решение

Разбиваем сечение на прямоугольник 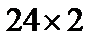и швеллер № 24 и проводим для каждой части главные центральные ос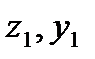и и .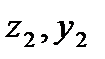

Площадь прямоугольника 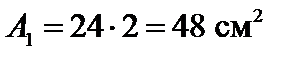, характеристи­ки швеллера определяем по сортаменту: А2 = 30,6 см2, Iz2 = = 2900 см2, .

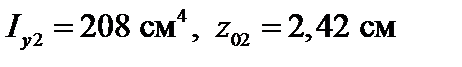Принимаем в качестве вспомогательных осей 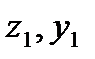и определяем координаты центра тяжести поперечного сечения по формулам (3.17):

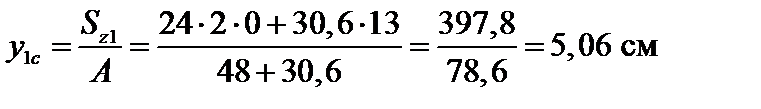– расстояние между осями 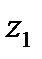и z;

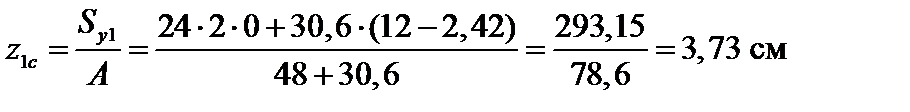– расстояние между осями 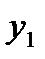и y (см. рис. 4.14).

Моменты инерции относительно центральных осей z, y (см. рис. 4.14):

 

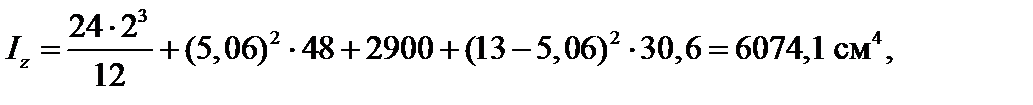
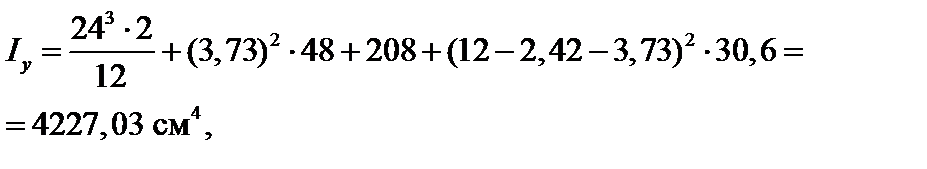
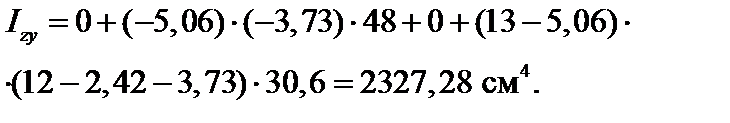
Величины главных центральных моментов инерции определяются с использованием формулы (3.20):

Важно:

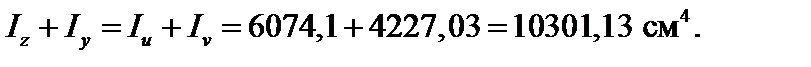
Положение главных центральных осей определяется с использованием формул (3.21):

Тогда угол между осями z и u будет отрицательным:

 

,

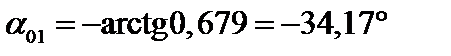откладывается по часовой стрелке (см. рис. 4.14). Угол между осями z и v будет положительным:

.

Положение главных центральных осей показано на рис. 4.15. Главные центральные радиусы инерции