4.1.4. Контрольные вопросы для самопроверки
1. К какому виду сопротивления относят осевое растяжение-сжатие (простому или сложному)?
2. Какие гипотезы вводят при расчете на осевое растяжение-сжатие?
3. Какое напряженное состояние возникает в элементе объема при данном виде сопротивления?
4. Сколько главных напряжений и какие отличны от нуля при центральном растяжении-сжатии?
5. Какие внутренние усилия возникают при осевом растяжении-сжатии в поперечных сечениях стержня, как обозначаются, какую размерность имеют?
6. Какие напряжения возникают при осевом растяжении-сжатии в поперечных сечениях стержня, как обозначаются, какую размерность имеют, по каким формулам определяются?
7. Какие факторы приводят к возникновению перемещений?
8. Какие перемещения возникают в случае центрального растяжения-сжатия, как их обозначают, какую размерность они имеют, по каким формулам определяются?
9. Какие правила знаков вводят для внутренних усилий, напряжений и перемещений при осевом растяжении-сжатии?
10. Какие условия прочности используют в осевом растяжении-сжатии?
11. Чем отличаются алгоритмы расчета на прочность для хрупкого и пластичного материалов?
12. Какие условия жесткости используют в случае центрального растяжения-сжатия?
13. Каков алгоритм расчета статически неопределимой системы при осевом растяжении-сжатии?
14. Какова разница расчета на прочность при осевом растяжении-сжатии по расчетным сопротивлениям и методу предельного равновесия?
4.2. Напряженно-деформированное состояние материала в точке. Геометрические характеристики сечений
4.2.1. Задача 2.1
Дан элемент объема в плоском напряженном состоянии, материал – малоуглеродистая сталь (рис. 4.12а).
Требуется:
1. Определить главные напряжения и положение главных площадок.
2. Найти экстремальные касательные напряжения и положение соответствующих им площадок.
3. Найти деформации в направлении заданных осей x, y и главные деформации.
4. Проверить выполнение условий прочности по различным теориям прочности: 1) теория максимальных нормальных напряжений; 2) теория наибольших линейных деформаций; 3) теория максимальных касательных напряжений; 4) энергетическая теория; 5) теория прочности Кулона–Мора.
Решение
1. Согласно выбранным координатным осям x, y s x = 120 МПа, s y = –100 МПа, t yx = –80 МПа. Величины главных напряжений определяются выражением (3.13):
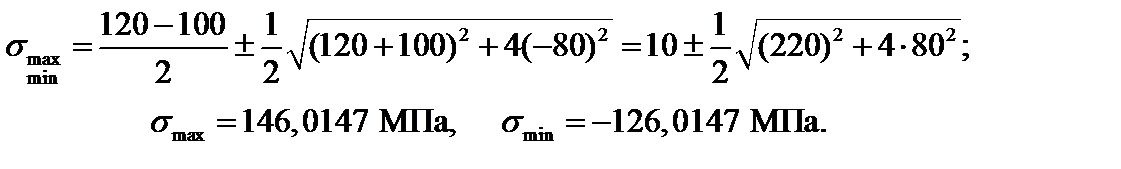
С учетом принятого правила индексации главных напряжений (3.12) в данном случае
.
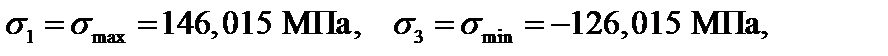
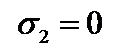При этом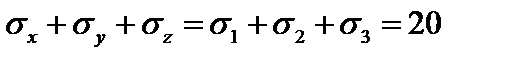 
МПа.
Направления векторов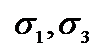 
определяются углами 
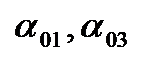. Из (3.14) получим:
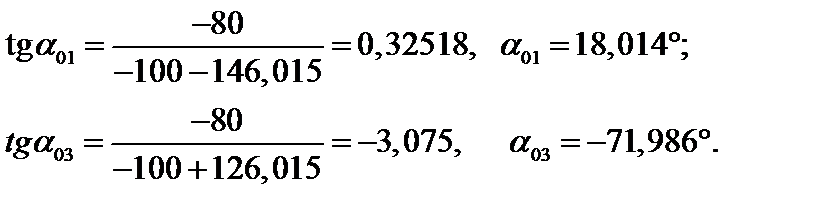
Положения главных площадок показаны на рис. 4.12б.
2. Величины экстремальных касательных напряжений определяются формулой (3.15):
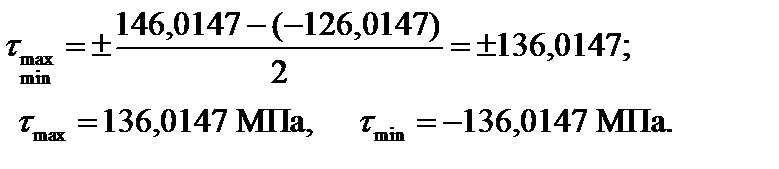
Угол между главными площадками и площадками с экстремальными касательными напряжениями равен 45°. Экстремальные касательные напряжения направлены в сторону максимального главного напряжения, при этом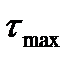 
действует по часовой стрелке, 
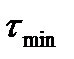– против. Положения площадок и касательные напряжения показаны на рис. 4.12б.
3. Линейные и угловые деформации определяются по закону Гука (3.16). Все механические характеристики выбираются по табл. П.1 (см. Приложение).
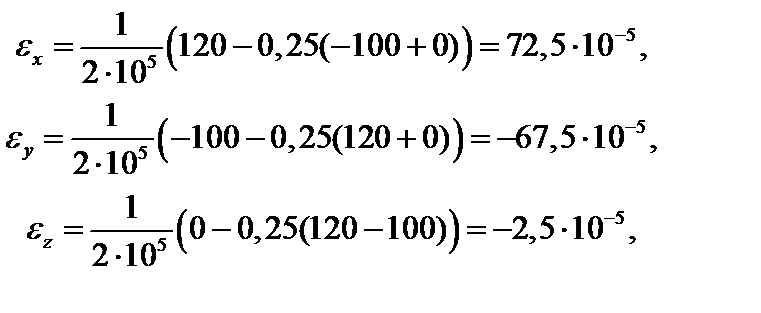
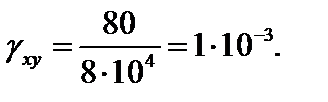
Главные деформации определяются аналогично:
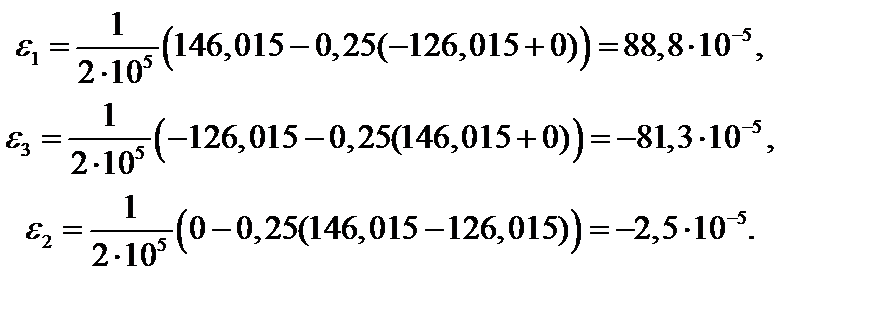
4. Проверка выполнения условий прочности
Согласно первой теории прочности
.
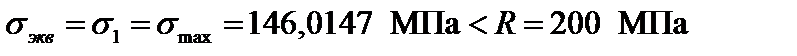По первой теории прочность обеспечена.
Согласно второй теории прочности
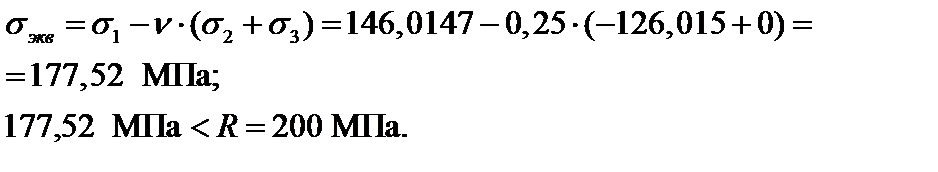
По второй теории прочность обеспечена.
Согласно третьей теории прочности
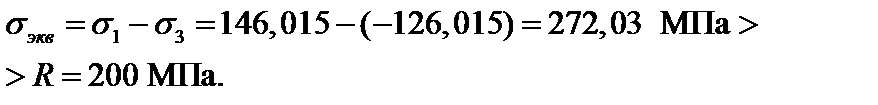
По третьей теории прочность не обеспечена.
Согласно четвертой теории прочности
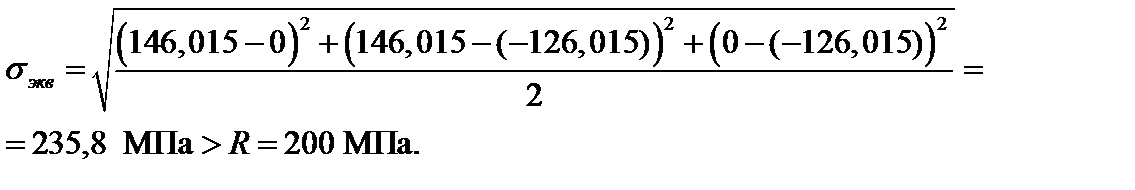
По четвертой теории прочность не обеспечена.
Так как для малоуглеродистой стали, которая является пластичным материалом, используется третья или четвертая теория прочности, можно сделать вывод, что прочность материала в исследуемой точке не обеспечена.
4.2.2. Задача 2.2
Для заданного поперечного сечения стержня (рис. 4.13) требуется:
1. Определить координаты центра тяжести сечения и провести главные центральные оси.