Статическая сторона задачи
Рассматриваемая задача один раз статически неопределима (четыре неизвестных реакций N1, N2, V О, H О в связях и три уравнения статики для определения этих раций). Из трех уравнений равновесия системы в данном случае удобно использовать только уравнение моментов относительно т. О:
∑ m О = 0; F∙1,5 + q·4·2 – N1∙3 + N2·4 = 0. (1)
Для раскрытия статической неопределимости требуется еще одно уравнение, которое составляется на основе рассмотрения двух других сторон задачи.
Геометрическая сторона задачи
Рассмотрение геометрической стороны задачи предполагает анализ возможной деформации системы и нахождение уравнения связи между деформациями стержней j, k.
| 1 |
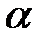
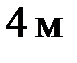


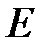
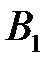
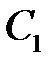
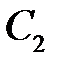
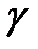
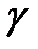
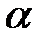
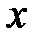
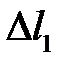
| 2 |
| x |
| y |
| Рис. 4.11 |
Примем в качестве возможной деформацию системы при повороте бесконечно жесткого стержня ОВС вокруг центра вращения О по часовой стрелке на бесконечно малый угол γ (рис. 4.11). В таком случае перемещения ВВ1, СС1 узлов системы перпендикулярны и пропорциональны радиусам вращения ОВ, ОС, а деформации стержней равны суммам проекций перемещений концов стержней на направления стержней: Δl1 = ВВ1, Δl2 = –СС2. Так как СС2 = СС1∙cos a = СС1∙0,8, а ВВ1/СС1 = ОВ/ОС = 0,6, то отношение
Δl1/ Δl2 = ВВ1/(–СС2) = –0,75. (а)
Физическая сторона задачи
Абсолютная деформация стержней (при отсутствии температурного воздействия) определяется как Δl i = N i·l i/ЕA i. Отсюда следует:
Δl1 = N1 · l1 /ЕA1 = N1 · 1 / (2 · 108 · А); (б)
Δl2 = N2 · l2 /ЕA2 = N2 · 2 / (1 · 108 · 2·А). (в)
С учетом уравнения (а) и соотношений (б), (в) получим:
(N1 · 1) / (2 · 108 · А) = –0,75 · (N2 · 2) / (1 · 108 · 2 · А).
После преобразований придем к соотношению между усилиями:
N1 = –1,5 N2. (2)
Решая систему уравнений (1), (2), получим: N1 = 1058,8 кН, N2 = = –705,9 кН. Статическая неопределимость задачи раскрыта.
2. Определение параметра А для площадей поперечных сечений.
Из условий прочности для стержней ВЕ и С D
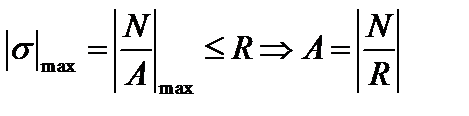 .
.
Найдем площадь для каждого стержня. Необходимо учесть при этом заданное по условию задачи соотношение площадей:
AВЕ = А = N1 / RВЕ = 1058,8 / (200 · 103) = 52,9 · 10–4 м2 Þ А = 52,9 см2;
AС D = 2А = |N2|; RС D = 705,9 / (120 · 103) = 58,8·10–4 м2 = 58,8 см2 Þ Þ А = 29,4 см2.
Окончательно принимаем наибольшую площадь А = 52,9 см2.
3. Расчет по предельной несущей способности
Найдем параметр Flim, соответствующий предельному состоянию системы. Для этого используем уравнение (1), подставив в него усилия
N1lim = σ s,ВЕ · AВЕ = 300 ·103 · 52,9 · 10–4,
N2lim = –σ s,СD · AС D = –180 · 103 · 2 · 52,9 · 10–4,
соответствующие предельному состоянию:
F lim ∙ 1,5 + 3/4 Flim · 4 · 2 – N1lim ∙ 3 + N2lim ·4 = Flim ∙ 1,5 +
+ 3/4Flim · 4 · 2 – 300 · 103 · 52,9 · 10–4 – 180 · 103 · 2 · 52,9 · 10–4 = 0. (3)
Из (3) получим: F lim = 1653 кН.
Тогда Fadm = F lim / k = 1653 / 1,5 = 1102 кН > 800 кН.
Таким образом, расчет по предельной несущей способности дает большие значения допустимого параметра Fadm силовой нагрузки, чем расчет с использованием условий прочности и расчетных сопротивлений.








