2. Построить эпюры продольных сил N, нормальных напряжений s и перемещений u.

Дата: 2025-05-25; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Решение

Допустим, что под действием силы и при повышении температуры стержень удлиняется и зазор ∆ = 10^–4 м закрывается. Тогда в точке В возникнет опорная реакция. Разобьем стержень на грузовые участки, выставим в начале и конце каждого участка сечения, назначим систему координат, направив при этом ось абсцисс вниз так, чтобы ее положительное направление соответствовало положительной продольной силе, растягивающему напряжению и положительному перемещению.

1. Определение опорных реакций

Статическая сторона задачи. Составим уравнение равновесия:

∑X = 0; R_А – R_В – ql_II + F = 0.

Определим степень статической неопределимости как разницу между неизвестными опорными реакциями и количеством уравнений статики n_st = 2 – 1 = 1 – задача один раз статически неопределимая, и для раскрытия статической неопределимости требуется еще одно уравнение.

Геометрическая сторона задачи. В случае удлинения стержня перемещение свободного конца составит ∆ = 10^–4 м.

u_В = Δl_I + Δl_II + Δl_III = ∆ = 10^–4 м.

Физическая сторона задачи. Абсолютную деформацию грузового участка в зависимости от того, чем она вызвана, можно представить в виде следующих зависимостей:

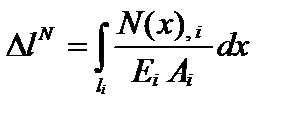– для грузового участка, где действует равномерно распределенная нагрузка;

– для грузового участка с постоянным внутренним усилием. Деформация, вызванная температурным воздействием, .

Подставим зависимости, полученные при рассмотрении физической стороны задачи, в уравнение для определения перемещения свободного конца стержня и получим уравнение совместности деформаций:

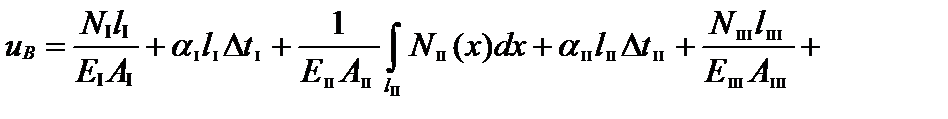
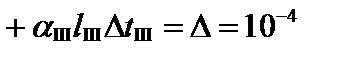м.

Запишем зависимости внутренних усилий на грузовых участках, отбросив при этом нижнюю заделку, и заменим ее влияние неизвестной опорной реакцией R_В:

N_I = – R_В + F – ql_II – const;

N_II = – R_В – qx₂ – линейная зависимость;

N_III = – R_В – const.

Подставим эти выражения в уравнение совместности деформаций и получим:

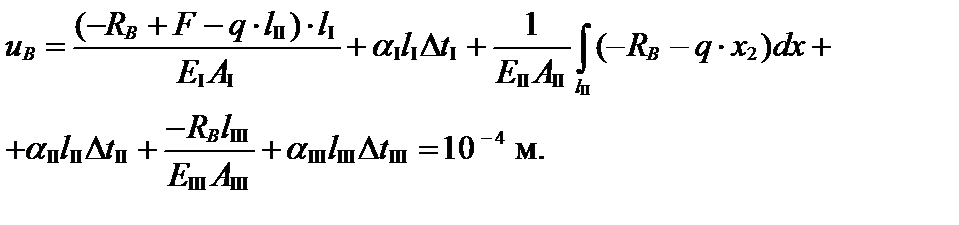
После подстановки числовых значений имеем уравнение с одним неизвестным:

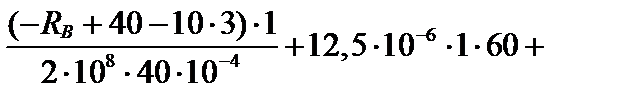
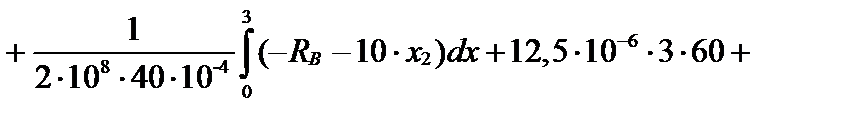
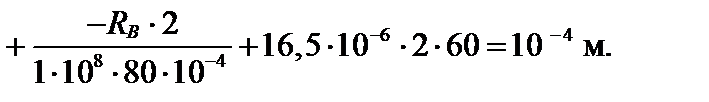
После интегрирования функции внутреннего усилия на втором грузовом участке получим:

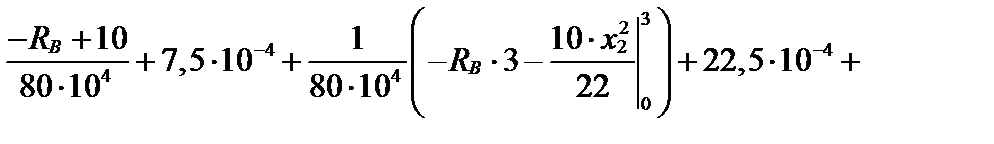
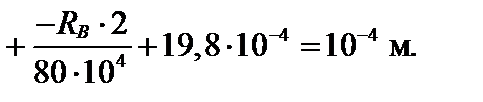
Умножим обе части уравнения на 10⁴, приведем к одному знаменателю, упростим и окончательно получим:

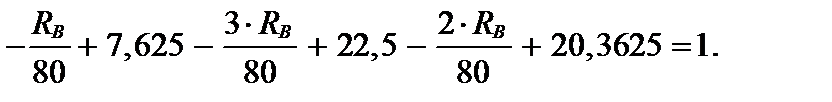
Dl_I Dl_II Dl_III

Решим уравнение относительно R_B и получим: R_B = 659,833 кН.

Значение опорной реакции положительно, значит, под действием силы и при температурном расширении стержень удлинился и зазор закрылся, как и было предположено раньше. Подставим значение R_B в последнее уравнение и умножим обе части на 10^–4, в результате получим перемещение каждого грузового участка, последовательное суммирование которых дает перемещение всего стержня, равное величине зазора:

(–0,623 – 2,244 + 3,867) ·10^–4 = 1·10^–4 м.

После определения опорной реакции R_B статическая неопределимость раскрыта, задача решается как статически определимая. Строятся эпюры продольной силы, напряжений и перемещений.

2. Построение эпюр

Построение эпюры продольной силы

N_I = –R_В + F – q · l_II = –659,833 + 40 – 10·3 = –649,833 кН;

N_1-1 = N_2-2 = –649,833 кН;

N_II = –R _В – q · x₂ = –659,833 – 10 · x₂;

N_3-3 = –689,833кН;

N_4-4 = –659,833кН;

N_III = –R _В = –659,833 кН;

N_5-5 = N_6-6 = –659,833 кН.

Построение эпюры напряжений

s_1-1 = s_2-2 = N_1-1/А₁ = (–649,833∙10^–3)/(40∙10^–4) = –162,458 МПа;

s_3-3 = N_3-3/А₁ = (–689,833) / (40∙10^–4) = –172,458 МПа;

s_4-4 = N_4-4/А₁ = (–659,833∙10^–3)/(40∙10^–4) = –164,958 МПа;

s_5-5 = s_6-6 = N_5-5 /А₂ = (–659,833∙10^–3)/(80∙10^–4) = –87,291 МПа.

Построение эпюры перемещений

u_2-2 = u_3-3 = u_1-1 + Δl_I = 0 – 0,623∙10^–4 = –0,623∙10^–4 м;

u_4-4 = u_5-5 = u_3-3 + Δl_II = (–0,523 – 2,244)∙10^–4 = –2,867∙10^–4 м;

u_6-6 = u_5-5 + Δl_III = (–2,867 + 3,867)∙10^–4 = 1 · 10^–4 м.

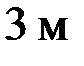
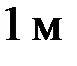
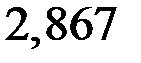
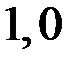
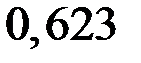
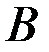
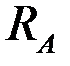
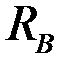
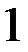
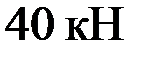
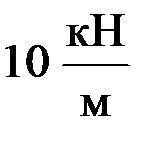
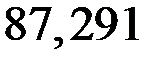
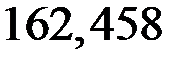
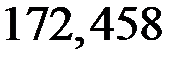
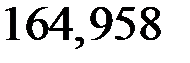
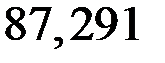
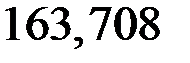
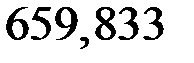
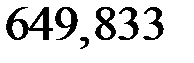
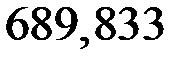
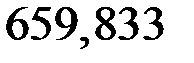
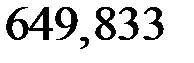
Рис. 4.9

4.1.3. Задача 1.3. Статически неопределимая стержневая система

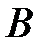
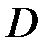
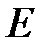
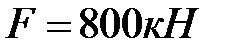
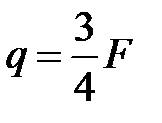
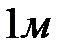
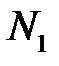
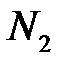
Рис. 4.10

Дано: ОВС – жесткий стержень; стержень ВЕ: Е_ВЕ = 2·10⁵ МПа, R_ВЕ = 200 МПа, σ _s,ВЕ = 300 МПа, площадь поперечного сечения А; стержень С D: Е_{С D} = 1·10⁵ МПа, R_{С D} = 120 МПа, σ _s,СD = 180 МПа, площадь поперечного сечения 2А.

Требуется:

1. Определить усилия в стержнях при действии силы F.

2. Определить параметр площади поперечного сечения А.

3. Найти значение параметра нагрузки F_lim по методу предельного равновесия и допустимое значение силы F_adm. Сравнить F_adm с заданной нагрузкой. Принять коэффициент запаса прочности для обоих стержней k = 1,5.

Решение

1. Определение усилий N₁, N₂ в стержнях.