Глава 4. Примеры решения задач по темам индивидуальных заданий (контрольных работ). Контрольные вопросы для самопроверки
4.1. Осевое растяжение-сжатие стержней
4.1.1. Задача 1.1. Статически определимая система








| Рис. 4.1 |
Дано: стойка из бетона жестко закреплена на нижнем конце и нагружена силами F1, F2 и q, действующими вдоль оси стержня. F1 = 120 кН, F2 = 150 кН, q = 40 кН/м, Е = 0,27·105 МПа, Rt = = 0,9 МПа, Rс = 12 МПа.
Требуется:
1. Построить эпюру продольных сил N.
2. Определить требуемые площади поперечных сечений А из условий прочности и соблюдения при этом заданного соотношения площадей на различных участках.
3. Построить эпюру нормальных напряжений σ.
4. Построить эпюру перемещений сечений u.
5. Выполнить проверку жесткости. [Δl] = (0,01 ÷ 0,02) l, [u] = = 0,001 l.
Решение
1. Построение эпюры продольных сил N
Разобьем стержень на грузовые участки. Для построения эпюры необходимо на всех грузовых участках с использованием метода сечений получить выражения для функции продольной силы. При рассмотрении грузовых участков используем локальные системы координат (оси x, y).
Рассмотрим первый грузовой участок.






























Рис. 4.2
Вырезая верхнюю часть и составляя уравнение равновесия вырезанной части, получим:
∑X = 0; N1(x) + F1 = 0 = > N1(x) = –F1 = –120 кН = const, N1–1 = = N2–2 = –120 кН.















 Рассмотрим второй грузовой участок:
Рассмотрим второй грузовой участок:
∑ X = 0; N2(x) + F1 – F2 = 0 =>
=> N2(x) = –F1 + F2 = –120 + 150 = = 30 кН = const, т.е. N3–3 = N4–4 = 30 кН.
Рассмотрим третий грузовой участок: 0 ≤ x ≤ 4 м.





















 ∑ X = 0; N3(x) + F1 – F2 + q· x = 0 =>
∑ X = 0; N3(x) + F1 – F2 + q· x = 0 =>
=> N3 (x) = – F1 + F2 – q· x = 30 – 40· x – линейная зависимость.
Тогда при x = 0 N5–5 = 30 кН, а при x = 4 м N6–6 = 30 – 40·4 = – 130 кН.
В пределах третьего грузового участка внутреннее усилие меняет знак, найдем расстояние от заделки до сечения, в котором N3 (x) = 0: x = 130 / 40 = 3,25 м (при этом значении x функция перемещений u3 (х) имеет экстремум).
Эп. N [кН]





























Рис. 4.3
2. Определение площади поперечных сечений А из условий прочности
Зная, что при центральном сжатии (растяжении) s = N(x)/A и учитывая заданное соотношение между площадями на грузовых участках (I, II – 2А, III – А), построим эпюру напряжений через отношения N(x) / A. Эта эпюра строится с целью нахождения опасных сечений. Выполним необходимые вычисления:
s1–1 = σ2–2 = N1–1 / 2 А = – 120 / 2 · А = – 60 / А;
s3–3 = σ4–4 = N3–3 / 2 А = 30 / 2 · А = 15 / А;
s5–5 = N5–5 /А = 30 / А;
s6–6 = N6–6 /А = – 130 / А.
Эп. N [кН] Эп. s





































Рис. 4.4
С помощью эпюры напряжений (Эп. s = Эп. N/ A) найдем опасные сечения. В настоящей задаче будет два опасных сечения, соответствующих экстремальным значениям напряжений (smin и smax):
– опасное сечение в растянутой зоне smax = s5–5 = 30/А;
– опасное сечение в сжатой зоне smin = s6–6 = –130/А.
Условие прочности при растяжении запишется как
smax = 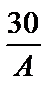 ≤ Rt = 900 кН/м2. Отсюда А ≥ 0,0333 м2.
≤ Rt = 900 кН/м2. Отсюда А ≥ 0,0333 м2.
Условие прочности при сжатии будет иметь вид:
|s|min ≤ Rс, |s|min = 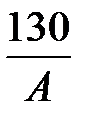 ≤ 12000 кН/м2. Отсюда А ≥ 0,0108 м2.
≤ 12000 кН/м2. Отсюда А ≥ 0,0108 м2.
Сравнивая найденные величины параметра площади сечения, примем к последующему расчету наибольшую, в данном случае найденную из условия прочности при растяжении: А = 0,0333 м2.
3. Построение эпюры нормальных напряжений s
Используя найденную из условий прочности величину параметра площади сечения, определяем величины нормальных напряжений в поперечных сечениях стержня:
s1–1 = s2–2 = –60 / А = – 60 / 0,333 = –1,8 · 103 кПа = –1,8 МПа;
s3–3 = s4–4 = 15 / А = 0,45 · 103 кПа = 0,45 МПа;
s5–5 = 30/А = 0,9 · 103 кПа = 0,9 МПа;
s6–6 = –130/А = –3,9 · 103 кПа = –3,9 МПа.
4. Построение эпюры перемещений u
Так как в данном случае стержень не подвергается температурному воздействию, выражение (3.5) для функции продольных перемещений сечений на участке i имеет вид:
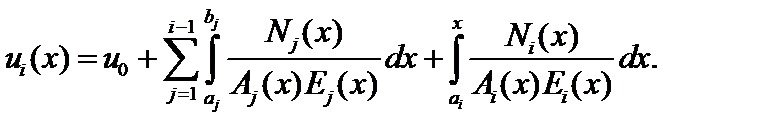 (4.1)
(4.1)
В данной задаче удобно за u0 принять перемещение в заделке, т.е. u6–6 = 0. Назначим начало координат в заделке, направим ось x вдоль стержня так, что положительные перемещения будут соответствовать положительному направлению оси. Определим опорную реакцию RB:
∑ X = 0; RB – F1 + F2 – q · 4 = 0; RB = 130 кН.
Запишем выражения для продольной силы на каждом грузовом участке:
N3 (x) = – RB + q · x = –130 + 40 x – линейная зависимость;
N2 (x) = –RB + q · 4 = –130 + 40 · 4 = 30 кН – const;
N1 (x) = –RB + q · 4 –F2 = –130 + 40 · 4 – 150 = –120 кН – const.
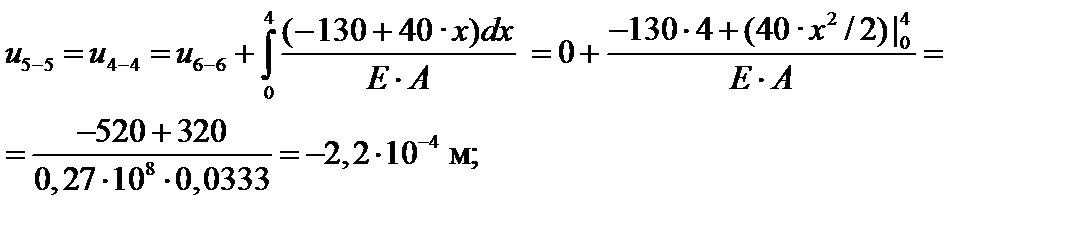
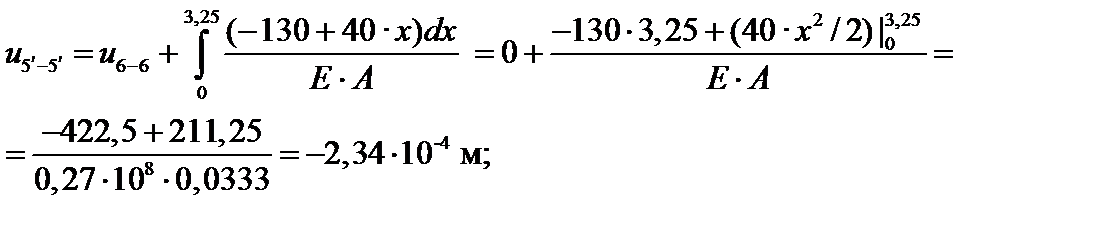
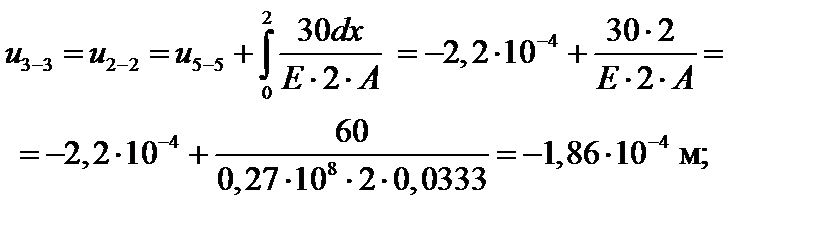
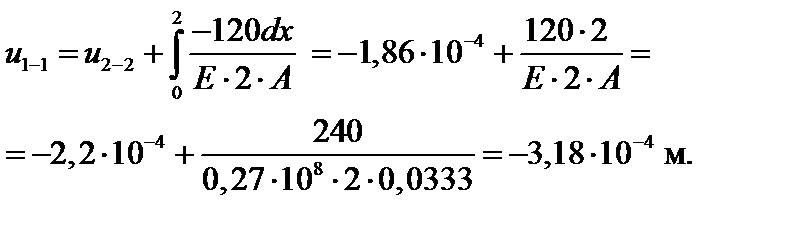
Найдя значения перемещений во всех сечениях (параболу строят по трем точкам), приступают к построению эпюры перемещений.

































| Эп. u [10–4 м] |
Рис. 4.5
Окончательно результаты расчетов представлены на рис. 4.6.








































| Эп. N [кН] Эп. s [МПа] Эп. u [10–4 м] |
Рис. 4.6
5. Проверка жесткости
Необходимо проверить выполнение условий жесткости: 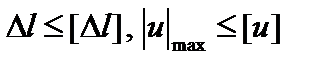 . Здесь ∆l – абсолютная деформация, т.е. перемещение свободного конца стержня, а │ u│max – максимальное по модулю перемещение сечения стержня, выбирается с помощью эпюры перемещений.
. Здесь ∆l – абсолютная деформация, т.е. перемещение свободного конца стержня, а │ u│max – максимальное по модулю перемещение сечения стержня, выбирается с помощью эпюры перемещений.
В данной задаче ∆ l = 3,18·10–4 м, │ u│max = 3,18·10–4 м, т.е. максимальное по модулю перемещение сечения и абсолютное изменение длины стержня совпадают.
[Δl] = 0,02·l = 0,02·8 = 0,16 м, [u] = 0,001·l = 0,001·8 = 0,008 м, тогда условия жесткости имеют вид:
0,000318 м < 0,16 м, 0,000318 м < 0,008 м.
Оба условия жесткости выполняются.
4.1.2. Задача 1.2. Статически неопределимая система
Дано: F = 40 кН, q = 10 кН/м, стойка изготовлена из двух различных материалов:








| Рис. 4.7 |
А1 = 40 см2, Е1 = 2·105 МПа,
α1 = 12,5 · 10–6 1/град; А2 = 80 см2,
Е2 = 1 · 105 МПа, α2 = 16,5 · 10–6 1/град.
Требуется:
1. Определить опорные реакции при действии сил F и q, увеличении температуры на Δt = 60° при наличии монтажного зазора между верхним концом бруса и опорой величиной ∆ = 0,1 мм = 1·10–4 м.








