Определение перемещений сечений плоских ломаных стержней и стержневых систем
Перемещения сечений плоских стержней и стержневых систем от заданной нагрузки (силовое воздействие) определяются по формуле Максвелла–Мора
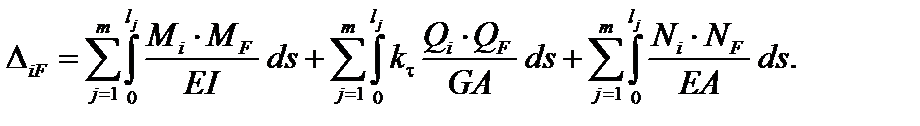 (3.59)
(3.59)
В этой формуле m – число участков; lj – длина j-го участка; 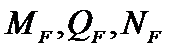 – внутренние силовые факторы (внутренние усилия) в действительном состоянии стержня (от заданной нагрузки);
– внутренние силовые факторы (внутренние усилия) в действительном состоянии стержня (от заданной нагрузки); 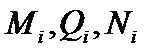 – усилия во вспомогательном состоянии стержня от единичного воздействия;
– усилия во вспомогательном состоянии стержня от единичного воздействия; 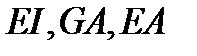 – жесткости сечений соответственно при изгибе, сдвиге, растяжении (сжатии);
– жесткости сечений соответственно при изгибе, сдвиге, растяжении (сжатии); 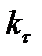 – коэффициент, учитывающий неравномерность распределения касательных напряжений в сечении при поперечном изгибе. Суммы берутся по всем участкам стержня.
– коэффициент, учитывающий неравномерность распределения касательных напряжений в сечении при поперечном изгибе. Суммы берутся по всем участкам стержня.
Выбор вспомогательного единичного состояния зависит от того, какое перемещение требуется найти. Если определяется линейное перемещение какого-либо сечения по определенному направлению, то в этом сечении по заданному направлению прикладывается единичная безразмерная сосредоточенная сила ( 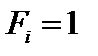 ). Если же требуется найти угол поворота какого-либо сечения, то в этом сечении прикладывается единичный сосредоточенный момент (
). Если же требуется найти угол поворота какого-либо сечения, то в этом сечении прикладывается единичный сосредоточенный момент ( 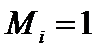 ), также безразмерный.
), также безразмерный.
При определении перемещений сечений плоских ломаных стержней и стержневых систем, преимущественно работающих на изгиб, влиянием поперечных и продольных сил пренебрегают, и тогда формула (3.59) принимает вид:
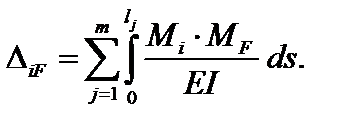 (3.60)
(3.60)
Будем рассматривать плоские ломаные стержни и стержневые системы, состоящие из прямолинейных элементов с постоянной жесткостью сечений при изгибе участков стержня. В этом случае получаем:
 (3.61)
(3.61)
Вычисление интегралов вида  на участке длиной
на участке длиной  , где в подинтегральное выражение входит произведение усилий
, где в подинтегральное выражение входит произведение усилий 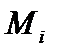 и
и 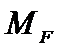 , являющихся ординатами эпюр изгибающих моментов, построенных для вспомогательного и действительного состояний, называют перемножением эпюр этих усилий.
, являющихся ординатами эпюр изгибающих моментов, построенных для вспомогательного и действительного состояний, называют перемножением эпюр этих усилий.
Перемножение эпюр может быть выполнено по формуле Симпсона:
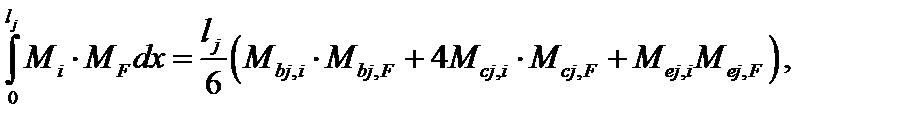 (3.62)
(3.62)
где  – изгибающие моменты в единичном (i-м) состоянии, действующие соответственно в начале, на конце и посередине j-го участка (в сечениях
– изгибающие моменты в единичном (i-м) состоянии, действующие соответственно в начале, на конце и посередине j-го участка (в сечениях  );
);  – изгибающие моменты в тех же сечениях в действительном (грузовом) состоянии F.
– изгибающие моменты в тех же сечениях в действительном (грузовом) состоянии F.
Отметим, что формула Симпсона дает точное значение определенного интеграла, если подинтегральная функция – полином не выше третьей степени. В частности, формула Симпсона дает точный результат, если перемножается эпюра 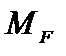 , очерченная по квадратной параболе, с прямолинейной эпюрой
, очерченная по квадратной параболе, с прямолинейной эпюрой 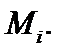
Произведение ординат перемножаемых эпюр в формуле (3.62) берется со знаком «плюс», если перемножаемые ординаты имеют один и тот же знак, и «минус» – если разные знаки.
Перемножение эпюр 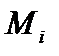 и
и 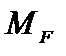 на участках с прямолинейной осью может быть выполнено и по правилу Верещагина в случае, когда одна из перемножаемых эпюр прямолинейна, а вторая может иметь любое очертание (прямолинейное, ломаное или криволинейное). Согласно этому правилу результат перемножения двух эпюр равен произведению площади одной из них на ординату другой (обязательно прямолинейной) эпюры, взятую под центром тяжести площади первой эпюры. В этом случае при EIj = const получаем:
на участках с прямолинейной осью может быть выполнено и по правилу Верещагина в случае, когда одна из перемножаемых эпюр прямолинейна, а вторая может иметь любое очертание (прямолинейное, ломаное или криволинейное). Согласно этому правилу результат перемножения двух эпюр равен произведению площади одной из них на ординату другой (обязательно прямолинейной) эпюры, взятую под центром тяжести площади первой эпюры. В этом случае при EIj = const получаем:
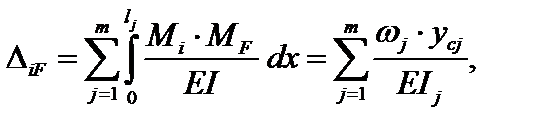 (3.63)
(3.63)
где w j – площадь одной из перемножаемых эпюр (прямолинейной, ломаной или криволинейной) на j-м участке;  – ордината второй (обязательно прямолинейной) эпюры, взятая под центром тяжести первой эпюры. Если перемножаемые эпюры расположены по одну сторону от оси эпюры, то результат берется со знаком «плюс», в противном случае – со знаком «минус».
– ордината второй (обязательно прямолинейной) эпюры, взятая под центром тяжести первой эпюры. Если перемножаемые эпюры расположены по одну сторону от оси эпюры, то результат берется со знаком «плюс», в противном случае – со знаком «минус».
Положительный знак определяемого перемещения указывает на то, что это перемещение совпадает с принятым направлением силы 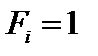 и
и 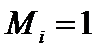 , а отрицательный знак – наоборот.
, а отрицательный знак – наоборот.
3.7.2. Задача 6.1
Стойка, выполненная из материала Ст3, R = 200 МПа, подвергается центральному сжатию силой F. Варианты поперечного сечения стойки приведены на рисунках ниже, остальные исходные данные – в табл. 6.1. Расчетные схемы стойки, соответствующие указанным значениям µ, показаны на рис. 3.17.
Требуется:
1. С помощью таблицы коэффициентов продольного изгиба подобрать поперечное сечение стойки заданной формы.
2. Подобранное сечение проверить на прочность при наличии ослабления Ant = 0,85 Abr.
3. Определить критическую силу и коэффициент запаса устойчивости.
4. Для подобранного сечения построить график зависимости критической силы и критического напряжения от длины и гибкости стержня, изменяя гибкость от 0 до 200.
Таблица 6.1
| Вид исходных данных | Варианты исходных данных к задаче 6.1 | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| l, м | 6 | 5 | 4 | 6 | 5 | 4 | 3 | 4 | 5 | 3 |
| F, кН | 400 | 450 | 500 | 550 | 600 | 650 | 700 | 680 | 720 | 750 |
| µ | 0,5 | 0,7 | 1 | 2 | 0,5 | 0,7 | 1 | 2 | 0,5 | 0,7 |








