Варианты расчетных схем к задаче 5.1
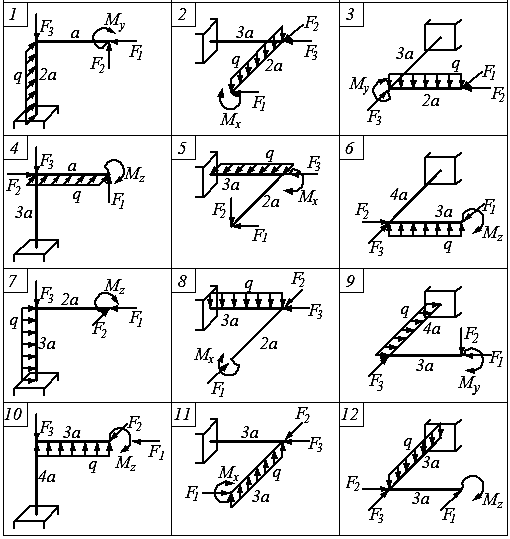

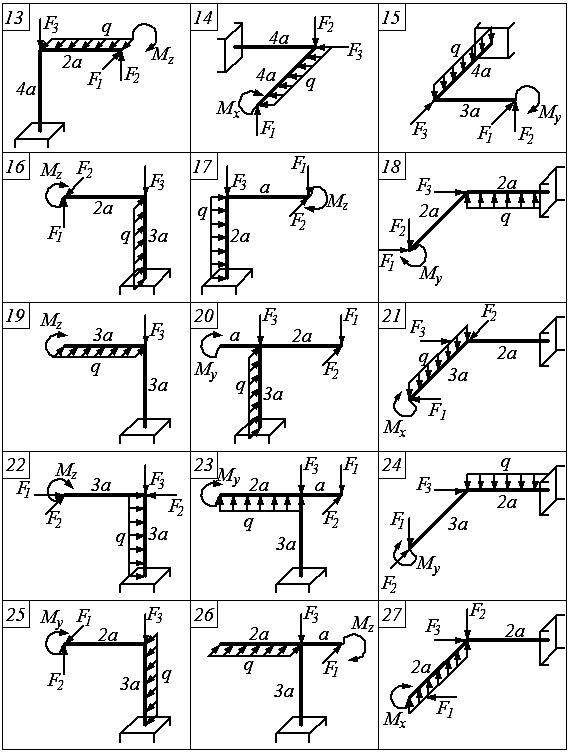

Направления моментных нагрузок Mx, My, Mz на расчетных схемах заданы следующим образом: при взгляде с положительного конца соответствующей оси пара вращается по часовой стрелке.
3.6.3. Задача 5.2
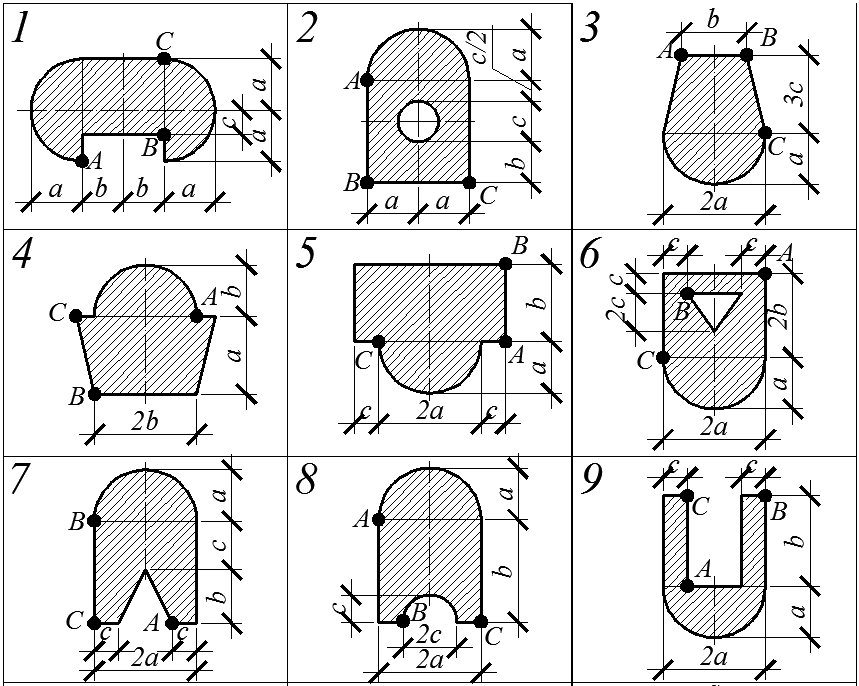
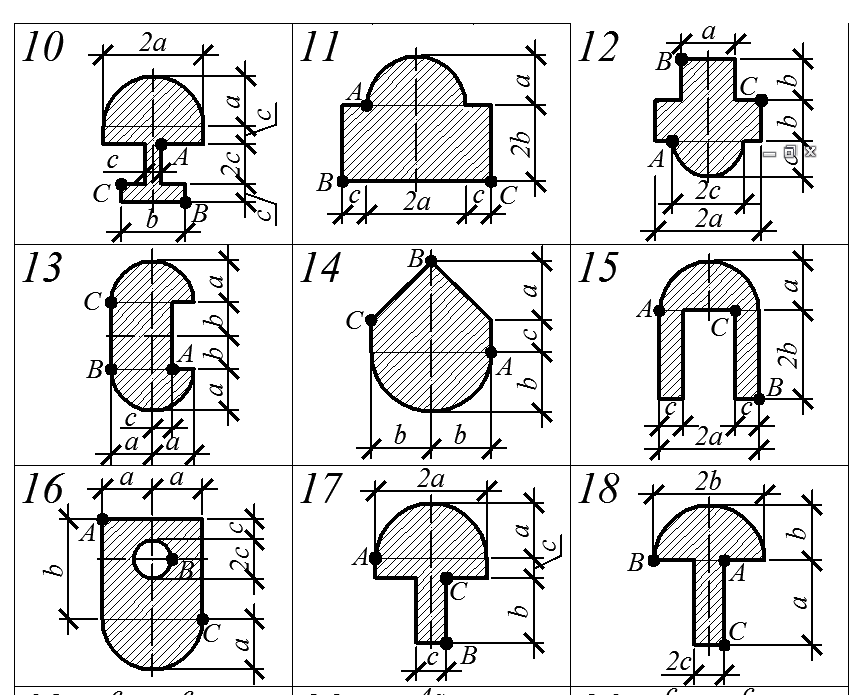
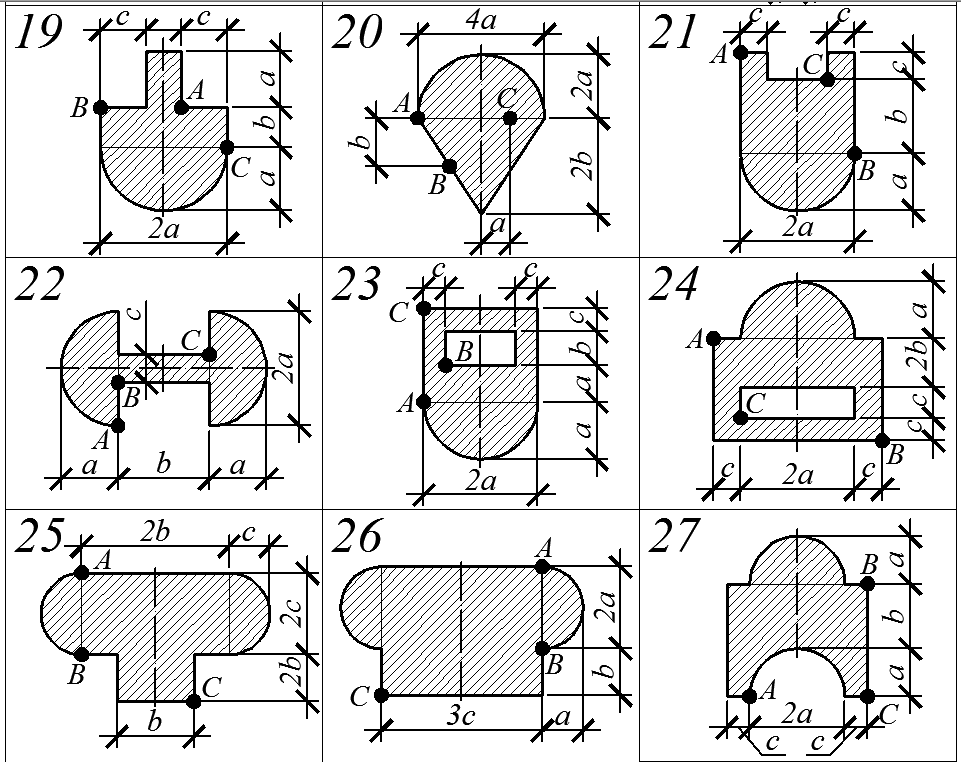
Короткий жесткий стержень, варианты поперечного сечения которого приведены на рисунке ниже, сжимается силой F, проходящей через заданную точку сечения и направленной параллельно продольной оси стержня.
Требуется:
1. Определить положение нейтральной оси заданного сечения, соответствующей заданному варианту нагружения.
2. Из условия прочности определить величину допускаемой силы [F].
3. При силе, равной [F], вычислить нормальные напряжения в точках сечения, наиболее удаленных от нейтральной оси в зонах растяжения и сжатия.
4. Построить эпюру нормальных напряжений в поперечном сечении стержня.
5. Построить ядро сечения.
Варианты исходных данных к задаче 5.2 приведены в табл. 5.2.
Таблица 5.2
| Вид исходных данных | Варианты исходных данных к задаче 5.2 | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| a, см | 30 | 26 | 20 | 48 | 48 | 45 | 36 | 64 | 56 | 55 |
| b, см | 24 | 22 | 16 | 34 | 30 | 30 | 24 | 40 | 42 | 35 |
| c, см | 12 | 14 | 10 | 18 | 16 | 20 | 16 | 20 | 12 | 10 |
| Точка приложения силы F | А | С | В | С | А | В | В | С | А | В |
| Rt, МПа | 2,2 | 4,2 | 5,4 | 3,5 | 2,8 | 3,6 | 2,4 | 4,3 | 2,6 | 3,8 |
| Rc, МПа | 12,1 | 40,5 | 60,5 | 36,2 | 30,4 | 42,2 | 38,1 | 58,1 | 32,4 | 45,5 |
Варианты расчетных схем к задаче 5.2
| 
| 
|

| 
| 
|

| 
| 
|
| 
| 
|

| 
| 
|

| 
| 
|
| 
| 
|

| 
| 
|

| 
| 
|
Примечания
Все криволинейные части контуров сечений являются дугой окружности.
Выбор варианта сечения при выполнении ИЗ (КР) проводится согласно методическим указаниям, приведенным в п. 3.1, аналогично выбору варианта расчетной схемы.
3.7. Индивидуальное задание 6 (контрольная работа 6). Расчет центрально-сжатого стержня на устойчивость. Определение перемещений сечений плоских ломаных стержней и стержневых систем
3.7.1. Краткие сведения из теории
Расчет центрально-сжатого стержня на устойчивость
Центрально-сжатый силой F прямолинейный стержень находится в состоянии устойчивого равновесия, если после отклонения стержня от этого прямолинейного состояния и устранения причины, вызвавшей отклонение, стержень возвращается в исходное состояние. Наименьшее значение сжимающей силы F, при которой первоначальная прямолинейная форма равновесия становится неустойчивой, называется критической силой (Fcr). При F = Fcr происходит раздвоение (бифуркация) форм равновесия.
Для обеспечения надежной работы конструкции сжатые стержни должны быть не только прочными и жесткими, но и находиться в состоянии устойчивого равновесия. Допускаемое значение сжимающей силы Fadm должно составлять лишь некоторую долю от критической силы Fcr:
Fadm = 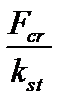 , (3.50)
, (3.50)
где kst > 1 – коэффициент запаса устойчивости.
В случае, когда потеря устойчивости наступает при упругой стадии работы материала стержня, т.е. при напряжениях меньше предела пропорциональности (  ), критическую сжимающую силу можно определять по формуле Эйлера:
), критическую сжимающую силу можно определять по формуле Эйлера:
 , (3.51)
, (3.51)
где Е – модуль упругости первого рода;  – минимальный момент инерции поперечного сечения стержня; l0 = m · l, l – длина стержня; m – коэффициент приведенной длины, зависящий от способа закрепления концов стержня.
– минимальный момент инерции поперечного сечения стержня; l0 = m · l, l – длина стержня; m – коэффициент приведенной длины, зависящий от способа закрепления концов стержня.
Значения  для некоторых расчетных схем стержня приведены на рис. 3.17.
для некоторых расчетных схем стержня приведены на рис. 3.17.




| m = 1 m = 2 m = 0,7 m = 0,5 |
Рис. 3.17
Напряжение в поперечном сечении сжатого стержня, вызываемое критической силой Fcr, называется критическим:
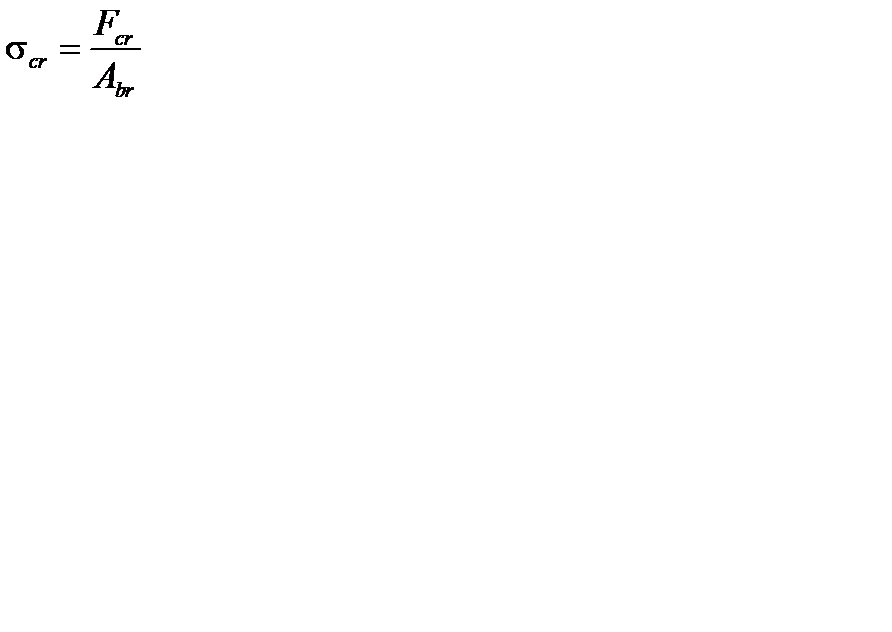 , (3.52)
, (3.52)
где  – площадь поперечного сечения брутто (без учета возможных ослаблений).
– площадь поперечного сечения брутто (без учета возможных ослаблений).
При критической силе, определяемой по формуле Эйлера (3.51), для критического напряжения получаем
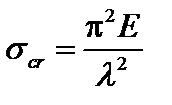 , (3.53)
, (3.53)
где 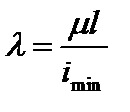 – гибкость стержня; (3.54)
– гибкость стержня; (3.54)
 – минимальный радиус инерции сечения.
– минимальный радиус инерции сечения.
Формулу (3.53) для критического напряжения, как и формулу Эйлера, можно использовать лишь тогда, когда критические напряжения не превосходят предела пропорциональности материала. Из условия  находим предельную гибкость:
находим предельную гибкость:
 . (3.55)
. (3.55)
Так, например, для стержней из Ст3 (Е = 2·105 МПа, s pr » » s e = 200 МПа) получаем l0 » 100.
Стержни, удовлетворяющие условию l ≥ l0, называются гибкими.
Для стержней, гибкость которых меньше некоторого значения lmin (жесткие стержни), критическое напряжение s cr может быть принято равным пределу текучести s S (пластичные материалы) или пределу прочности s u (хрупкие материалы). Для стержней средней гибкости lmin < l ≤ l0 критическое напряжение может быть найдено приближенно по эмпирической формуле Ф. Ясинского:
s cr = a – b l, (3.56)
где 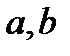 – коэффициенты, зависящие от материала стержня и имеющие размерность напряжения (приводятся в справочниках).
– коэффициенты, зависящие от материала стержня и имеющие размерность напряжения (приводятся в справочниках).
Зная критическое напряжение, можно найти и критическую силу:
 . (3.57)
. (3.57)
Для практического расчета центрально-сжатого стержня на устойчивость условие устойчивости удобно записать в виде:
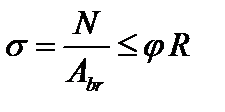 , (3.58)
, (3.58)
где N – продольная сила; R – расчетное сопротивление материала; j – коэффициент продольного изгиба (коэффициент уменьшения основного расчетного сопротивления при продольном изгибе).
Коэффициент j зависит от материала и гибкости стержня и приводится в таблицах. Пользуясь условием (3.58), можно решать следующие задачи:
1) делать проверочный расчет на устойчивость;
2) подбирать сечение стержня;
3) определять допускаемую нагрузку  .
.








