Изгиб с кручением (стержни круглого и кольцевого сечений).
Для стержней круглого и кольцевого сечений любая центральная ось сечения является главной центральной, и плоскость общей изгибающей пары в сечении с моментом
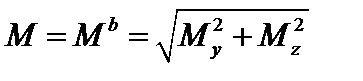
также является главной центральной. Экстремальные нормальные напряжения возникают на контуре сечения и равны
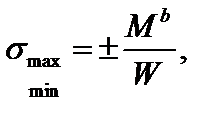(3.40)
где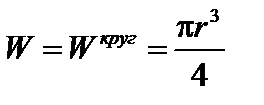 
– осевой момент сопротивления круглого сечения; 
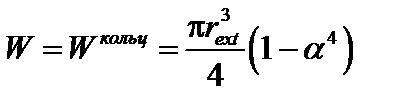– осевой момент сопротивления кольцевого сечения; r – радиус круглого сечения; rext, rint – внешний и внутренний радиусы кольцевого сечения; α = rint / rext.
Пренебрегая касательными напряжениями от изгиба стержня, получим следующую величину максимальных касательных напряжений в точках внешнего контура сечения:
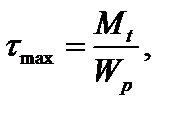(3.41)
где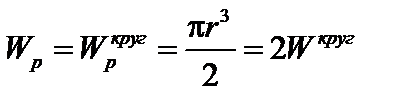 
– полярный момент сопротивления круглого сечения. Аналогично 
.
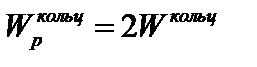Условия прочности по третьей теории прочности в опасных точках контура записывается в виде:
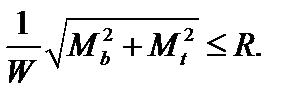(3.42)
Общий случай сложного сопротивления (стержни круглого и кольцевого сечений).
В общем случае сложного сопротивления стержней круглого и кольцевого сечений максимальные по абсолютной величине нормальные напряжения на контуре равны
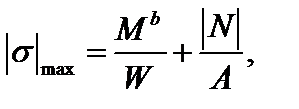(3.43)
где N – продольная сила в сечении; А – площадь сечения.
Условие прочности по третьей теории прочности имеет вид:
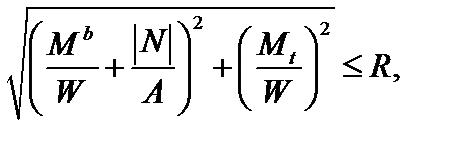(3.44)
где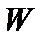 
– осевой момент сопротивления сечения (выражения представлены ранее);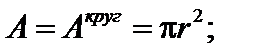 
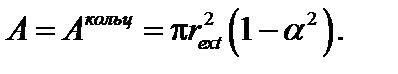
При решении задачи подбора сечения в данном случае удобно использовать метод последовательных приближений.
Внецентренное растяжение-сжатие жестких стержней.
|
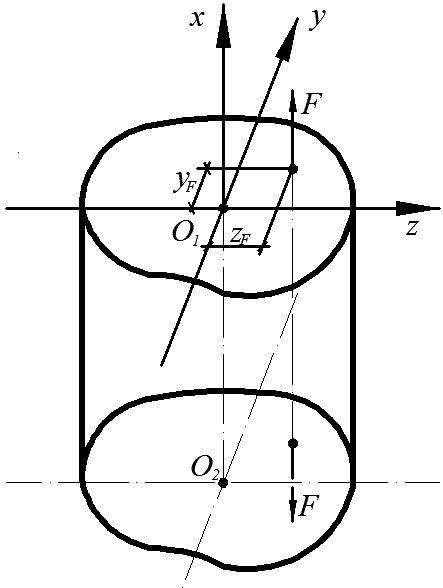
| Рис. 3.14 |
Данная форма сложного сопротивления стержня реализуется при нагружении прямого стержня, имеющего большую изгибную жесткость, силами, параллельными продольной оси стержня, но не проходящими через центр тяжести сечения (рис. 3.14).
Пусть стержень внецентренно нагружен силой F; yF, zF – координаты точек приложения силы F. В том случае, если не учитываются (в силу малости) деформации изгиба, данную форму сложного сопротивления можно представить как линейную сумму осевого растяжения (сжатия) с продольной силой N = F и чистых изгибов стержня в плоскостях xOy, xOz при действии изгибающих моментов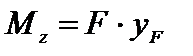 
, 
Нормальные напряжения в точках поперечного сечения определяются согласно соотношению
(3.45)
где 
– радиусы инерции сечения.
Уравнение нейтральной оси (н.о.) 
имеет вид:
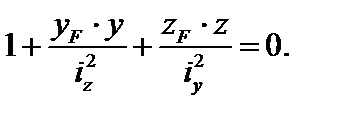
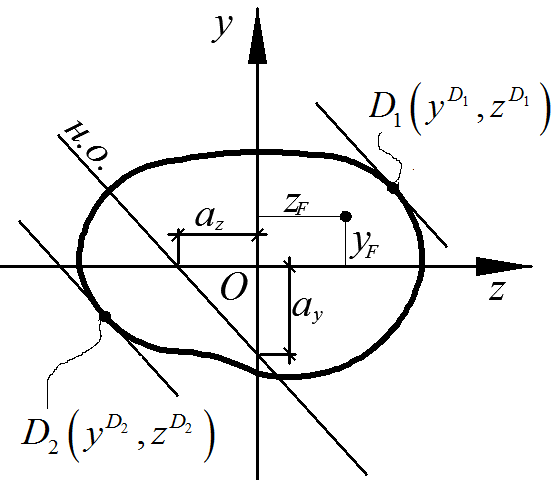Рис. 3.15
|
Таким образом, в данном случае н.о. – прямая, не проходящая через начало координат. Определяя отрезки, отсекаемые ею на осях y, z (рис. 3.15,), получим:
, (3.46)
Проводя касательные к сечению, параллельные н.о., найдем наиболее напряженные точки D1, D2 в зонах растяжения и сжатия. Условия прочности стержня по нормальным напряжениям принимают следующий вид:
а)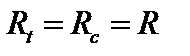 
– расчетное сопротивление материала стержня,
(3.47)
б) 
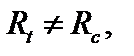
(3.48)
В том случае, если н.о. не пересекает сечения (напряжения в сечении имеют один знак), одно из условий (3.48) отсутствует.
Ядро сечения – область плоскости сечения, обладающая следующим свойством: продольная нагрузка, приложенная в пределах этой области, вызывает во всем сечении напряжения одного знака. Координаты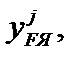 
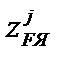точек границы ядра сечения определяются по формулам
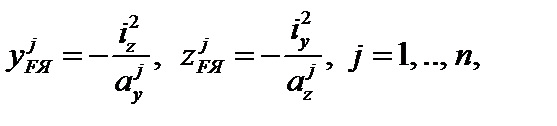(3.49)
где j – номер j-й касательной к сечению и соответствующей точки границы ядра сечения;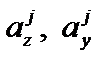 
– отрезки, отсекаемые на координатных осях j-й касательной к сечению; n – число рассматриваемых касательных к сечению.
3.6.2. Задача 5.1
Для пространственного ломаного стержня, варианты расчетных схем которого приведены ниже, требуется:
1. Построить эпюры внутренних усилий в поперечных сечениях стержня.
2. Определить форму сопротивления стержня на участках.
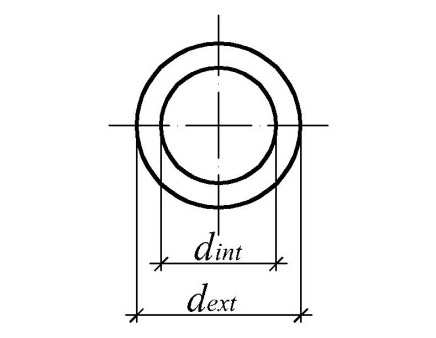
3. Подобрать сечение стержня на участках из условий прочности, приняв R = 210 МПа. При наличии кручения на участке принять сечение типа «Б» (рис. 3.16), в остальных случаях использовать сечение типа «А», выбрав рациональную ориентацию главных центральных осей инерции сечения.
| Сечение «A» | Сечение «Б» |
| 
|
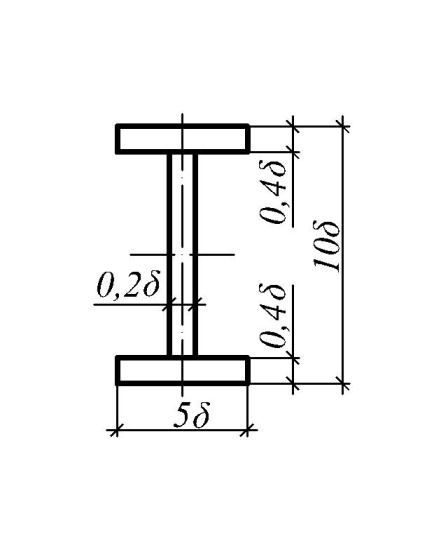
Рис. 3.16
Варианты исходных данных к задаче 5.1 приведены в табл. 5.1.
Таблице 5.1
| Вид исходных данных | Варианты исходных данных к задаче 5.1 | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| a, м | 1,0 | 1,8 | 1,2 | 2,0 | 1,4 | 1,6 | 1,8 | 2,0 | 1,0 | 1,4 |
| F1, кН | 30 | 25 | 28 | 22 | 24 | 32 | 40 | 26 | 30 | 36 |
| F2, кН | 20 | 15 | 25 | 30 | 32 | 18 | 20 | 40 | 16 | 30 |
| F3, кН | 800 | 900 | 1000 | 1200 | 900 | 1100 | 1000 | 800 | 1300 | 1400 |
| q, кН/м | 20 | 25 | 15 | 30 | 20 | 18 | 25 | 10 | 16 | 20 |
| Mx, My, Mz, кН·м | 30 | 20 | 24 | 36 | 40 | 18 | 22 | 16 | 20 | 35 |
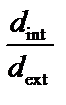
| 0,80 | 0,85 | 0,9 | 0,84 | 0,78 | 0,70 | 0,82 | 0,72 | 0,86 | 0,76 |