При прямом поперечном изгибе в различных точках поперечного сечения нормальные и касательные напряжения определяют по формулам
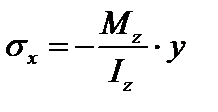 ,
, 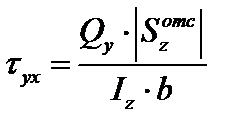 , (3.29)
, (3.29)
где Iz – момент инерции поперечного сечения относительно нейтральной оси Z; y – ордината точки (слоя) относительно нейтральной оси, в которой определяются напряжения (Mz и y подставляются с учетом знака); 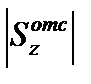 – статический момент отсеченной части (момент части площади поперечного сечения, расположенной выше или ниже слоя (точки), в котором определяются касательные напряжения, взятый относительно нейтральной оси Z); b – ширина слоя (сечения), в котором определяются касательные напряжения.
– статический момент отсеченной части (момент части площади поперечного сечения, расположенной выше или ниже слоя (точки), в котором определяются касательные напряжения, взятый относительно нейтральной оси Z); b – ширина слоя (сечения), в котором определяются касательные напряжения.
Подбор размеров сечения стержня при прямом поперечном изгибе производят по значению требуемого момента сопротивления, полученного из условия прочности по нормальным напряжениям:
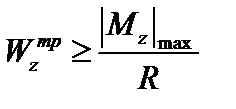 , (3.30)
, (3.30)
где R – расчетное сопротивление материала.
Для составных сечений момент сопротивления определяется для наиболее удаленных от нейтральной оси точек поперечного сечения стержня:
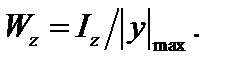 (3.31)
(3.31)
Подобранное сечение должно удовлетворять нескольким условиям прочности:
· 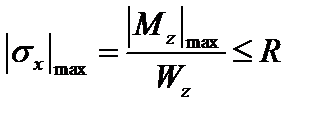 – по нормальным напряжениям;
– по нормальным напряжениям;
· 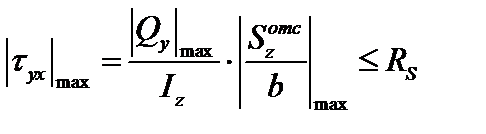 – по касательным напряжениям, где RS – расчетное сопротивление на сдвиг;
– по касательным напряжениям, где RS – расчетное сопротивление на сдвиг;
· 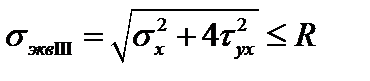 – по гипотезе наибольших касательных напряжений;
– по гипотезе наибольших касательных напряжений;
· 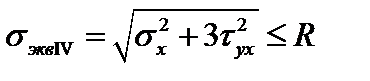 – по энергетической гипотезе прочности.
– по энергетической гипотезе прочности.
Причем каждое условие записывается для определенной точки поперечного сечения с соответствующими компонентами напряженного состояния и найденными расчетными усилиями.
Проведение указанных проверок подразумевает, что в любой точке любого поперечного сечения стержня рассматриваемые условия прочности должны выполняться.
Расчет по предельной несущей способности. Рассматривается состояние предельного равновесия стержня с образованием пластического шарнира в наиболее «нагруженном» его сечении. Предельный момент в пластическом шарнире
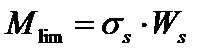 . (3.32)
. (3.32)
Пластический момент сопротивления 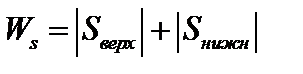 определяется как сумма статических моментов верхней и нижней частей поперечного сечения относительно оси, параллельной нейтральной и делящей площадь поперечного сечения на две равновеликие части (Аверх = Анижн).
определяется как сумма статических моментов верхней и нижней частей поперечного сечения относительно оси, параллельной нейтральной и делящей площадь поперечного сечения на две равновеликие части (Аверх = Анижн).
Расчетный момент, который может воспринять материал сечения, уменьшается относительно предельного при помощи коэффициента запаса k:
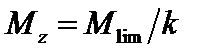 .
.
Тогда требуемый пластический момент сопротивления
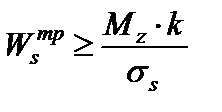
позволяет определить размеры сечения.
Определение перемещений поперечных сечений стержня при прямом поперечном изгибе (прогибов и углов поворота) проводят при помощи метода начальных параметров. Для этого используют универсальные выражения прогибов, углов поворота, изгибающих моментов и поперечных сил, начальные параметры которых определяют при помощи статических и кинематических граничных условий:
· для прогибов
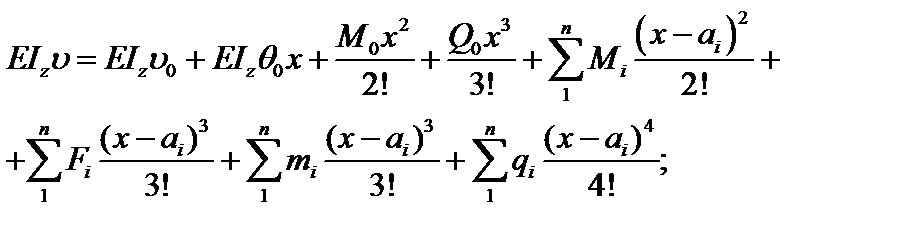 (3.33)
(3.33)
· для углов поворота
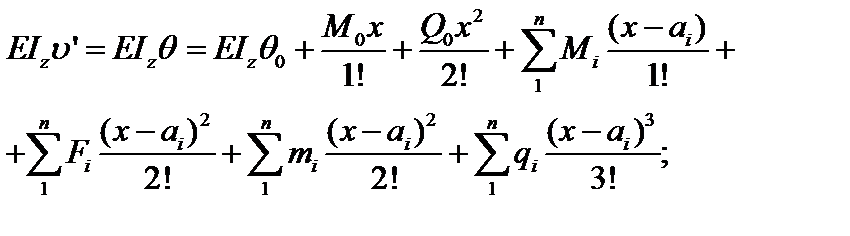 (3.34)
(3.34)
· для изгибающих моментов
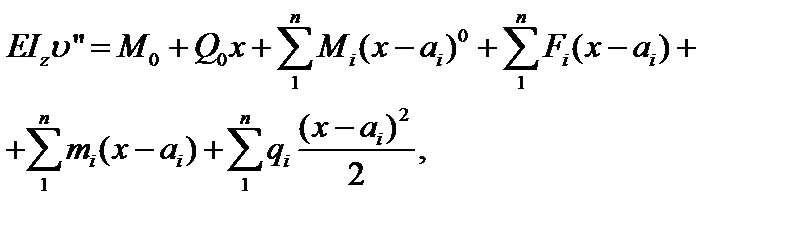 (3.35)
(3.35)
где 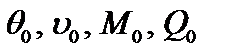 – начальные параметры.
– начальные параметры.
Для каждого грузового участка балки в универсальных уравнениях исключаются все члены, содержащие в скобках отрицательные значения.
Метод начальных параметров также применим к решению статически неопределимых задач.
3.5.2. Задача 4.1
Для балок, данные нагрузок и размеров которых приведены в табл. 4.1, а расчетные схемы даны ниже, требуется:
1. Определить реакции опор. Построить эпюры поперечных сил Qy и изгибающих моментов Mz. Определить положение опасных сечений.
2. Из условия прочности по нормальным напряжениям определить размеры поперечного сечения балки в двух вариантах: (а) и (б) (рис. 3.12). Принять R = 200 МПа.
а) б)
Рис. 3.12
3. Выполнить проверку прочности по касательным напряжениям. Принять Rs = 120 МПа.
4. Для варианта (б) поперечного сечения сделать проверку прочности материала в точке, в которой имеет место неблагоприятное сочетание нормальных s х и касательных 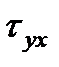 напряжений. Применить гипотезы прочности – наибольших касательных напряжений и энергетическую.
напряжений. Применить гипотезы прочности – наибольших касательных напряжений и энергетическую.
5. Для варианта (б) поперечного сечения определить его размеры из расчета по предельной несущей способности. Принять 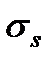 = 240 МПа, k = 1,2.
= 240 МПа, k = 1,2.
6. Для заданной балки записать уравнения прогибов и углов поворота по методу начальных параметров. Определить начальные параметры (сечение – вариант (а)).
7. Вычислить значение прогиба на расстоянии 3а (2а) и угла поворота на расстоянии 5а от начала координат.
8. Составить перечень исходных данных для расчета на ЭВМ. Выполнить расчет на ЭВМ. Результаты сравнить с данными, полученными вручную в п. 7.
9. По результатам расчета на ЭВМ построить эпюры углов поворота 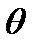 и прогибов
и прогибов 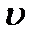 сечений балки.
сечений балки.
10. Проверить выполнение условия жесткости балки, приняв 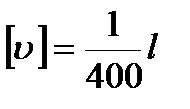 , где l – пролет балки (расстояние между опорами, или длина консольной части).
, где l – пролет балки (расстояние между опорами, или длина консольной части).
Таблица 4.1
| Вид исходных данных
| Варианты исходных данных к задаче 4.1
|
| 0
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
|
| q, кН/м
| 20
| 10
| 20
| 10
| 20
| 30
| 40
| 30
| 40
| 30
|
| F, кН
| 30
| 50
| 40
| 30
| 40
| 60
| 50
| 80
| 70
| 90
|
| M, кН×м
| 40
| 20
| 50
| 50
| 50
| 40
| 60
| 50
| 30
| 80
|
| a, м
| 2
| 2
| 2
| 2
| 2
| 1
| 1
| 1
| 1
| 1
|
Примечание для студентов ВиЗО
1. Выполнение пп. 8, 9 не обязательно.
2. Для п. 10 значение прогиба взять из пп. 6, 7.
Расчетные схемы балок к задаче 4.1
3.6. Индивидуальное задание 5 (контрольная работа 5). Сложное сопротивление стержней
3.6.1. Краткие сведения из теории
Сопротивление стержня называется сложным, если оно может быть представлено как сумма нескольких простых видов деформации стержня.
В реальных конструкциях при деформировании стержней присутствуют все виды простых деформаций (растяжение, сжатие, изгиб, кручение, сдвиг). Однако в ряде случаев, пренебрегая влиянием некоторых видов простых деформаций (в силу их малости), мы можем упростить истинную картину сложного сопротивления без существенного ущерба надежности сооружения. К таким упрощенным видам сложного сопротивления относятся: косой изгиб; изгиб с кручением; внецентренное растяжение-сжатие жестких стержней. Если пренебрегать влиянием части простых видов деформации нельзя, то мы имеем общий случай сложного сопротивления стержня.
В той постановке, которая принята в данном учебном пособии при рассмотрении сложного сопротивления стержней, в силу малости деформаций считается применимым принцип независимости действия сил (принцип суперпозиции).
Косой изгиб – сопротивление прямого стержня действию поперечных нагрузок, проходящих через центры изгиба сечений (то есть не вызывающих закручивания стержня), но не располагающихся только в одной главной плоскости инерции стержня (рис. 3.13). Будем полагать, что центры тяжести и центры изгиба сечений совпадают (сечения имеют две и более осей симметрии либо разницей положения центров тяжести и изгиба можно пренебречь).
а)
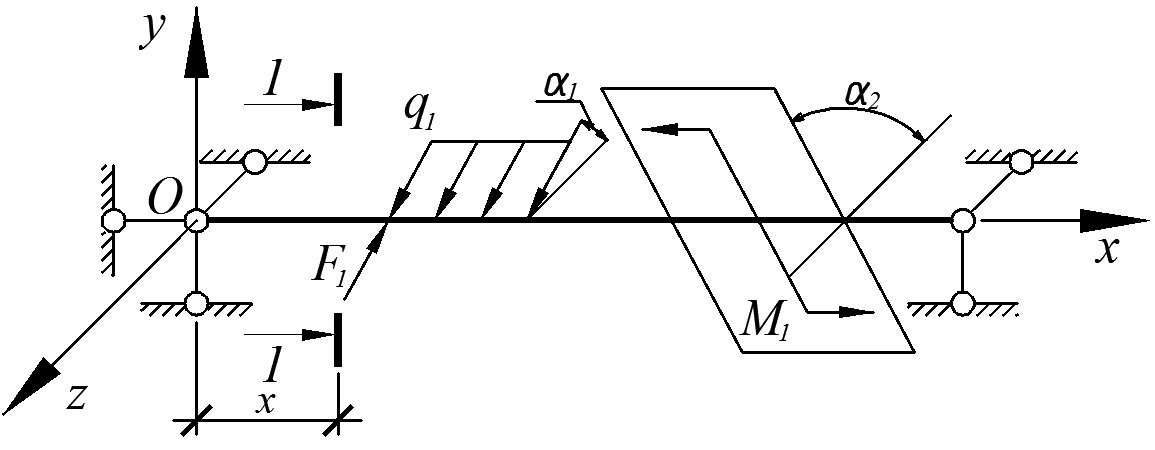
б)
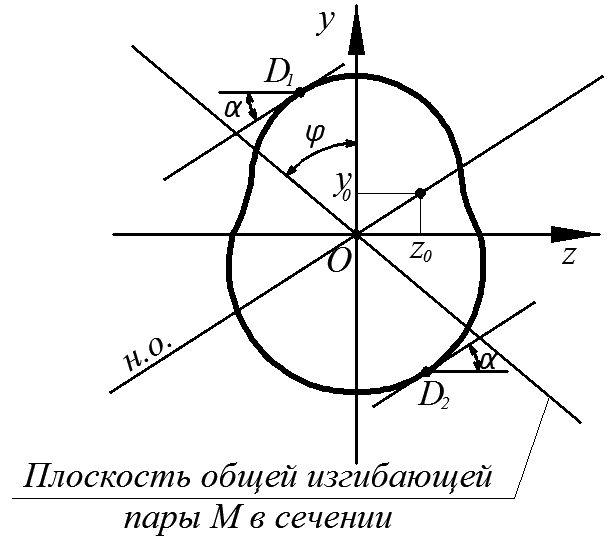
Рис. 3.13
Раскладывая нагрузки в главные плоскости инерции YOX, ZOX, можно рассматривать косой изгиб как сумму двух прямых изгибов стержня.
Нормальные напряжения в поперечных сечениях стержня равны
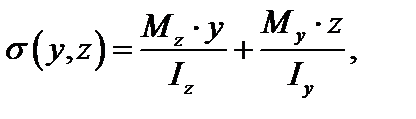 (3.36)
(3.36)
где Mz, My – изгибающие моменты в главных плоскостях YOX, ZOX.
Учитывая, что 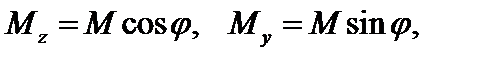 получим уравнение нейтральной оси (н.о.)
получим уравнение нейтральной оси (н.о.) 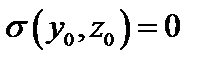 в виде
в виде
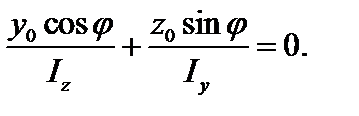
Отсюда
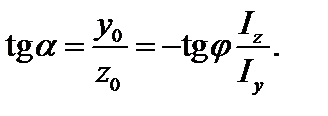 (3.37)
(3.37)
Экстремальные нормальные напряжения в сечении возникают в точках 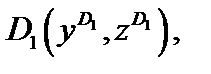
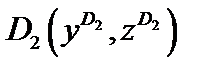 . Условия прочности по нормальным напряжениям при косом изгибе стержня имеют вид:
. Условия прочности по нормальным напряжениям при косом изгибе стержня имеют вид:
а) 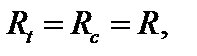
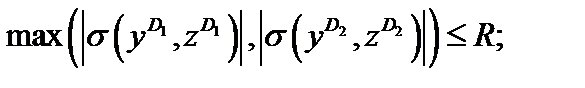 (3.38)
(3.38)
б) 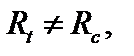
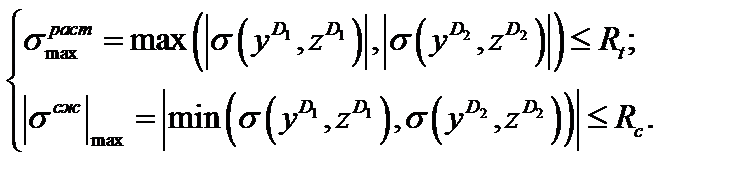 (3.39)
(3.39)
Условия (3.38), (3.39) используются для решения проектных задач при расчете стержня на прочность.
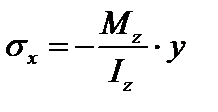 ,
, 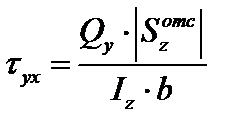 , (3.29)
, (3.29)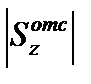 – статический момент отсеченной части (момент части площади поперечного сечения, расположенной выше или ниже слоя (точки), в котором определяются касательные напряжения, взятый относительно нейтральной оси Z); b – ширина слоя (сечения), в котором определяются касательные напряжения.
– статический момент отсеченной части (момент части площади поперечного сечения, расположенной выше или ниже слоя (точки), в котором определяются касательные напряжения, взятый относительно нейтральной оси Z); b – ширина слоя (сечения), в котором определяются касательные напряжения.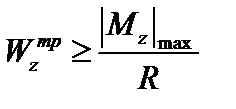 , (3.30)
, (3.30)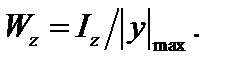 (3.31)
(3.31)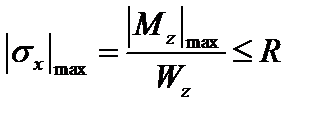 – по нормальным напряжениям;
– по нормальным напряжениям;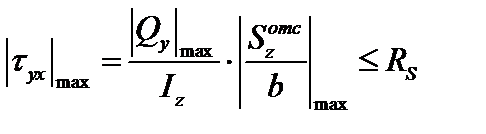 – по касательным напряжениям, где RS – расчетное сопротивление на сдвиг;
– по касательным напряжениям, где RS – расчетное сопротивление на сдвиг;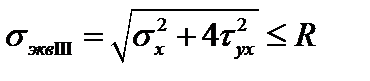 – по гипотезе наибольших касательных напряжений;
– по гипотезе наибольших касательных напряжений;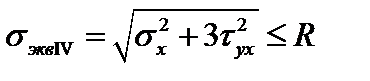 – по энергетической гипотезе прочности.
– по энергетической гипотезе прочности.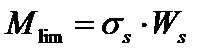 . (3.32)
. (3.32)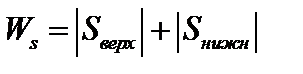 определяется как сумма статических моментов верхней и нижней частей поперечного сечения относительно оси, параллельной нейтральной и делящей площадь поперечного сечения на две равновеликие части (Аверх = Анижн).
определяется как сумма статических моментов верхней и нижней частей поперечного сечения относительно оси, параллельной нейтральной и делящей площадь поперечного сечения на две равновеликие части (Аверх = Анижн).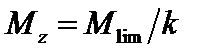 .
.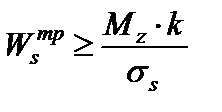
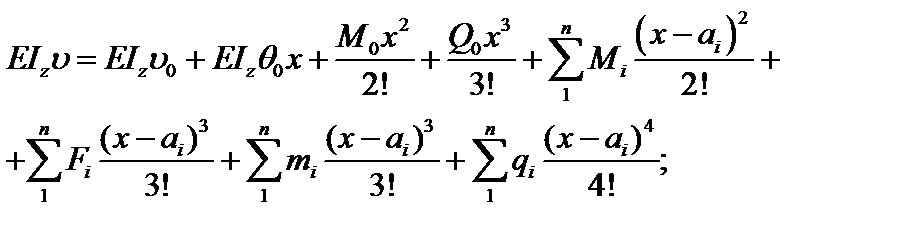 (3.33)
(3.33)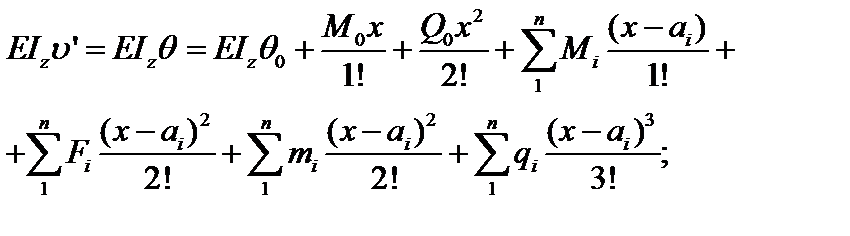 (3.34)
(3.34)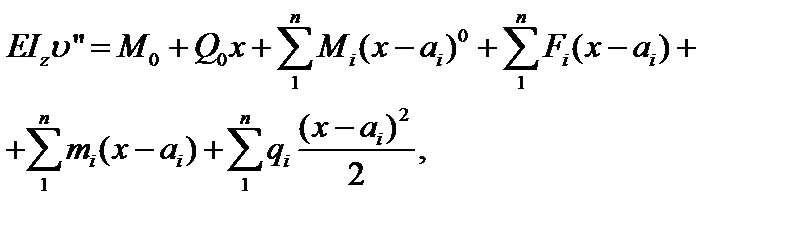 (3.35)
(3.35)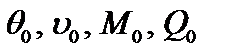 – начальные параметры.
– начальные параметры.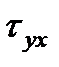 напряжений. Применить гипотезы прочности – наибольших касательных напряжений и энергетическую.
напряжений. Применить гипотезы прочности – наибольших касательных напряжений и энергетическую.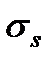 = 240 МПа, k = 1,2.
= 240 МПа, k = 1,2.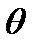 и прогибов
и прогибов 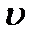 сечений балки.
сечений балки.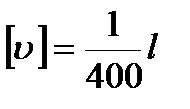 , где l – пролет балки (расстояние между опорами, или длина консольной части).
, где l – пролет балки (расстояние между опорами, или длина консольной части).

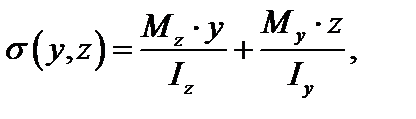 (3.36)
(3.36)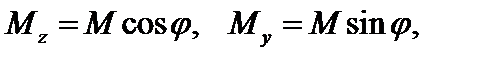 получим уравнение нейтральной оси (н.о.)
получим уравнение нейтральной оси (н.о.) 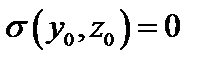 в виде
в виде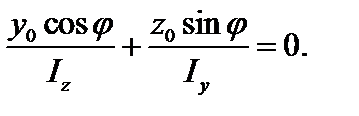
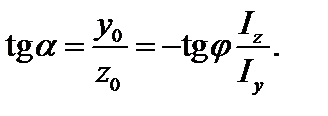 (3.37)
(3.37)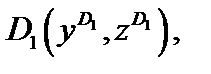
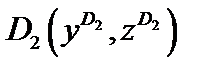 . Условия прочности по нормальным напряжениям при косом изгибе стержня имеют вид:
. Условия прочности по нормальным напряжениям при косом изгибе стержня имеют вид: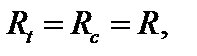
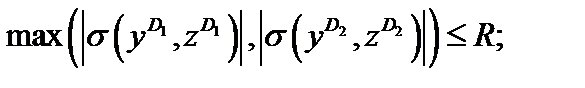 (3.38)
(3.38)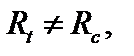
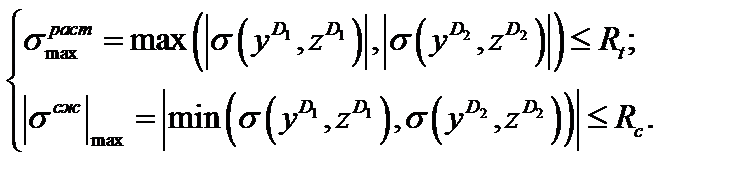 (3.39)
(3.39)







