Варианты расчетных схем к задаче 3.1
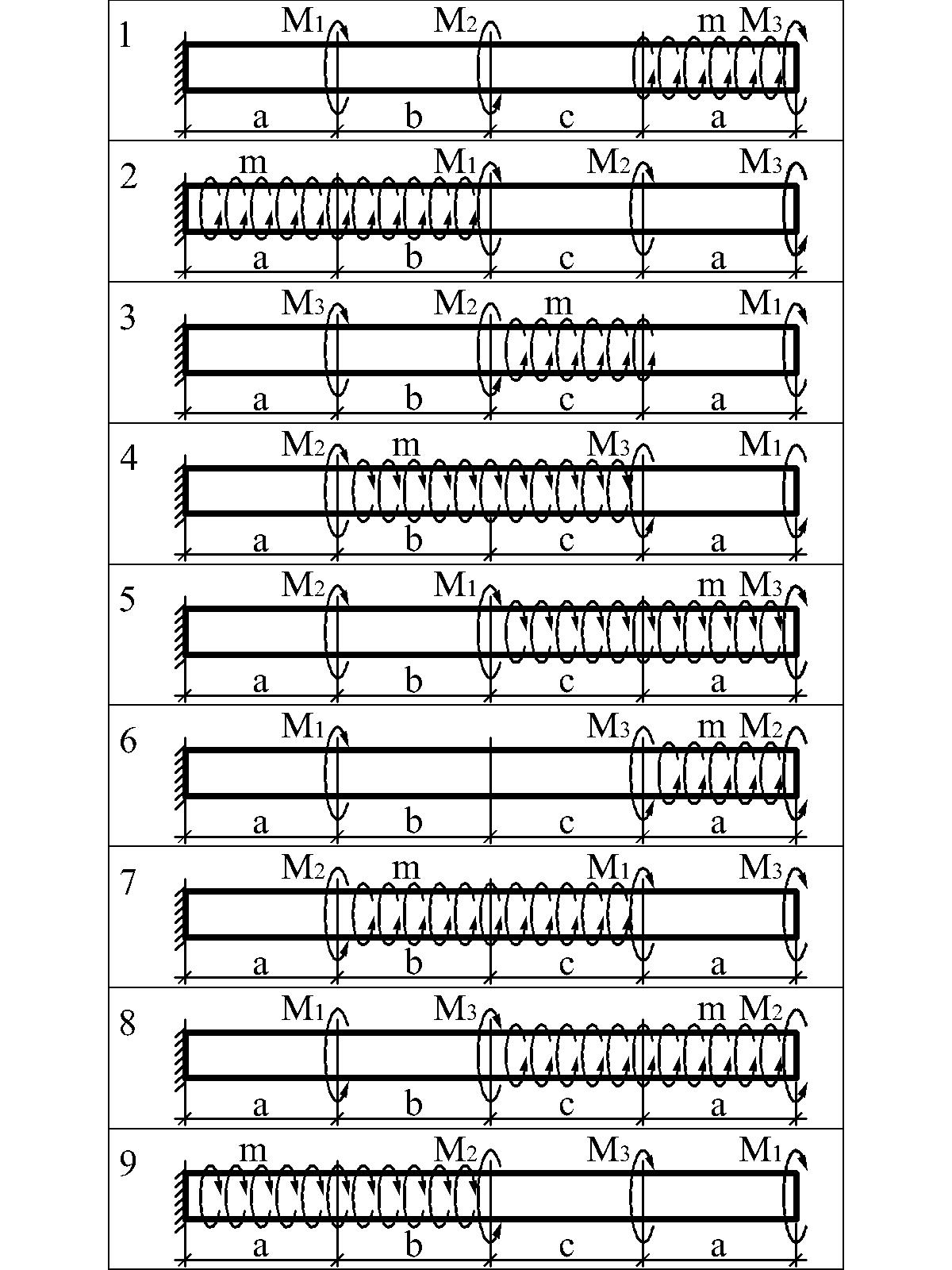
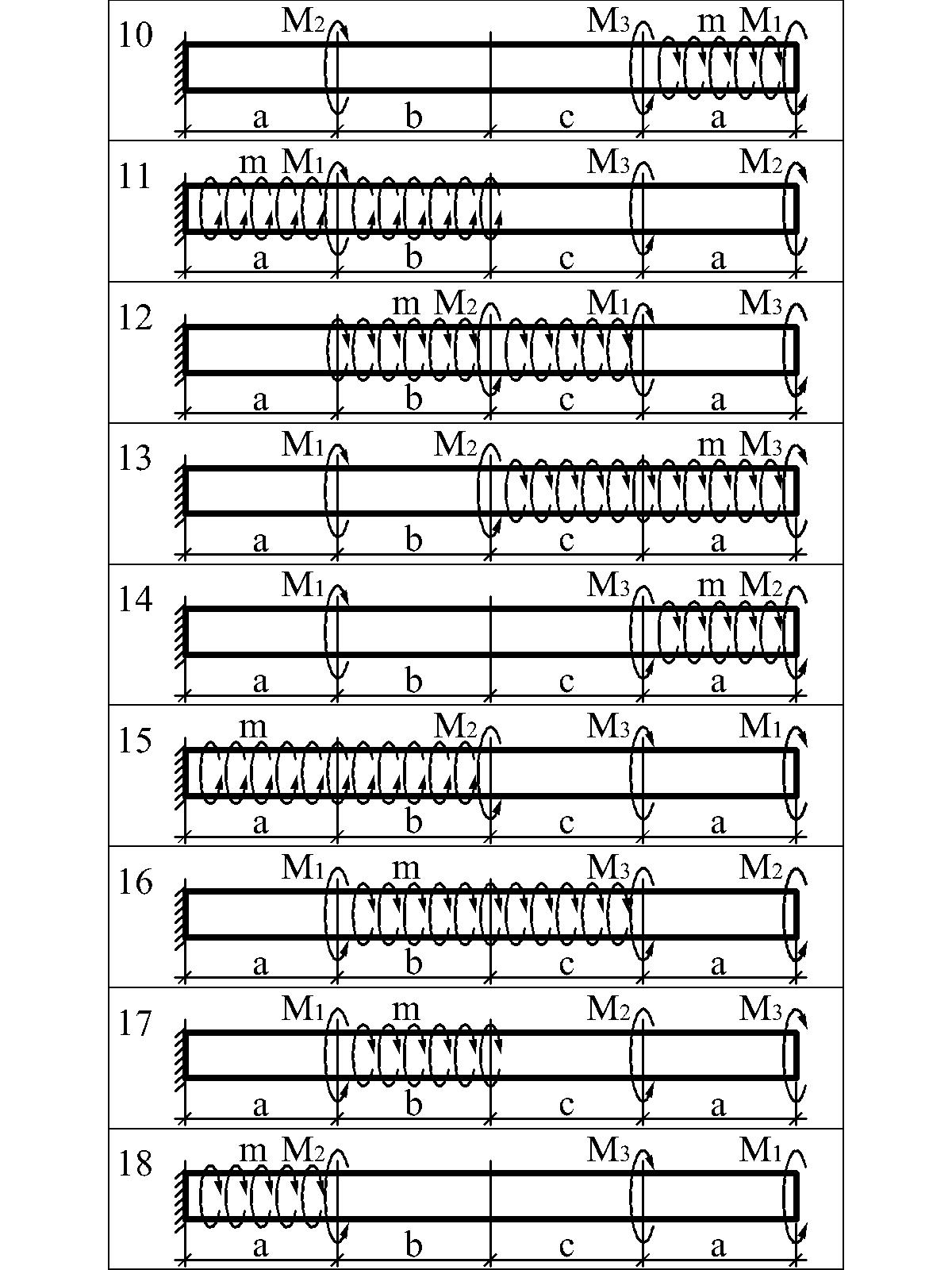
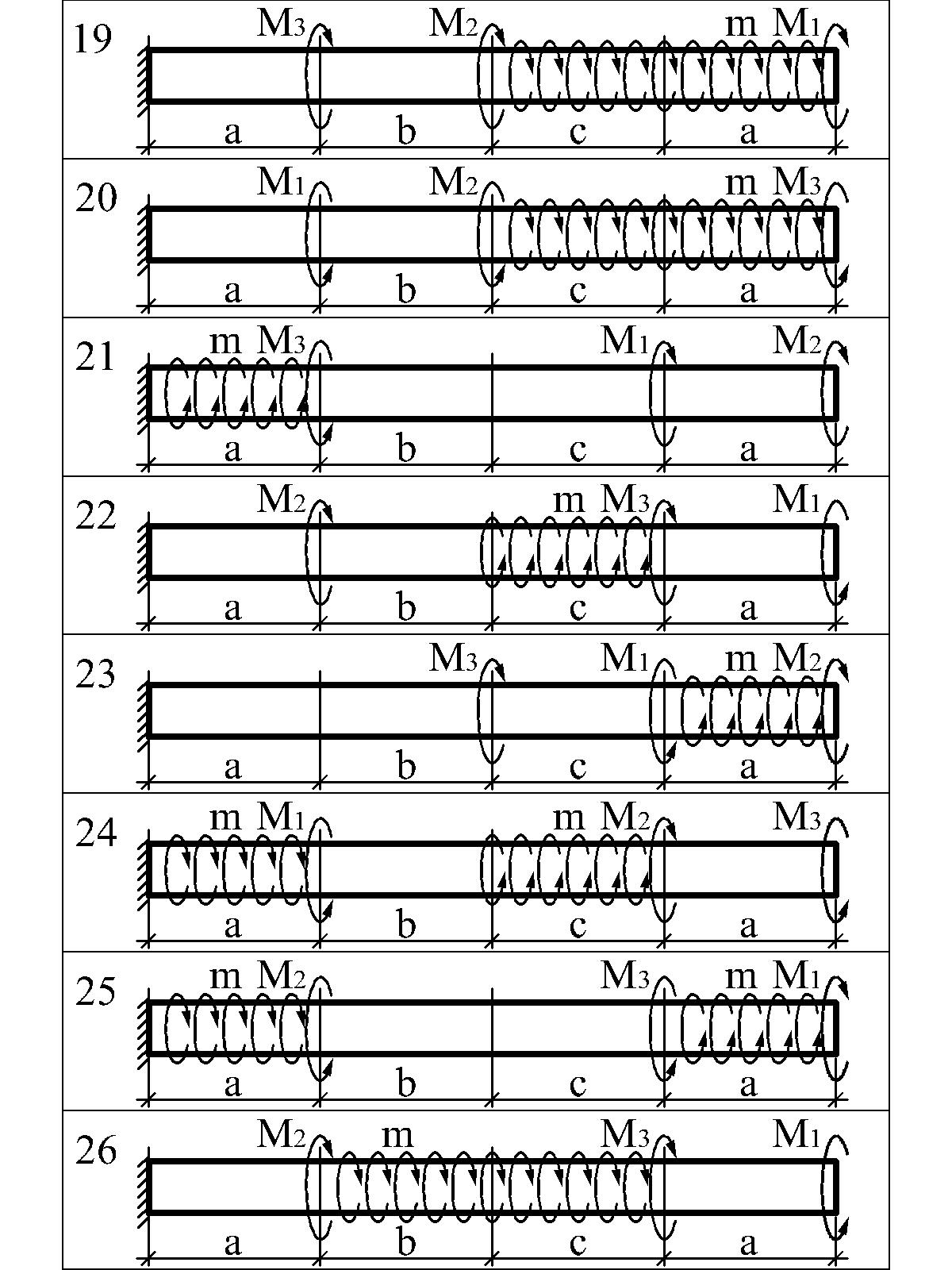
3.4.3. Задача 3.2
Варианты расчетных схем стержней для статически неопределимой задачи 3.2 при кручении приведены ниже. Задан вариант поперечного сечения стержня (см. рис. 3.11а – круглое сечение).
Требуется:
1. Построить эпюру Mt в предположении линейно-упругой работы материала.
2. По условию прочности (расчет по несущей способности) подобрать круглое поперечное сечение стержня.
3. Подобрать круглое сечение стержня из условия расчета по предельной нагрузке, выражая М1, М2, М3 через величину m согласно исходным данным.
4. Сравнить результаты расчетов по расчетному сопротивлению (несущей способности) и по предельной нагрузке.
Варианты остальных исходных данных к задаче 3.2 представлены в табл. 3.2.
Таблица 3.2
| Вид исходных данных | Варианты исходных данных к задаче 3.2 | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| a, м | 1,2 | 1,1 | 1,0 | 1,2 | 0,8 | 1,3 | 0,7 | 1,2 | 0,8 | 1,1 |
| b, м | 0,8 | 1,3 | 1,4 | 1,0 | 1,1 | 0,7 | 1,2 | 0,9 | 1,1 | 0,7 |
| c, м | 1,0 | 0,7 | 0,8 | 0,7 | 1,2 | 0,9 | 1,3 | 1,1 | 1,4 | 1,5 |
| М1, кН·м | 2,1 | 1,8 | 2,3 | 1,9 | 1,6 | 1,8 | 2,3 | 2,2 | 1,9 | 2,1 |
| М2, кН·м | 1,8 | 2,2 | 1,4 | 2,5 | 2,6 | 1,5 | 1,2 | 1,4 | 2,1 | 1,4 |
| М3, кН·м | 1,9 | 1,6 | 1,8 | 1,3 | 1,2 | 2,1 | 1,6 | 1,8 | 1,6 | 1,8 |
| m, кН·м/м | 1,0 | 1,2 | 1,3 | 1,1 | 0,8 | 1,4 | 1,2 | 1,0 | 1,3 | 1,5 |
| Rs, МПа | 100 | 90 | 80 | 70 | 60 | 70 | 80 | 90 | 100 | 80 |
| t s, МПа | 120 | 117 | 112 | 105 | 84 | 91 | 96 | 117 | 140 | 120 |
| k | 1,2 | 1,3 | 1,4 | 1,5 | 1,4 | 1,3 | 1,2 | 1,3 | 1,4 | 1,5 |
Варианты расчетных схем к задаче 3.2
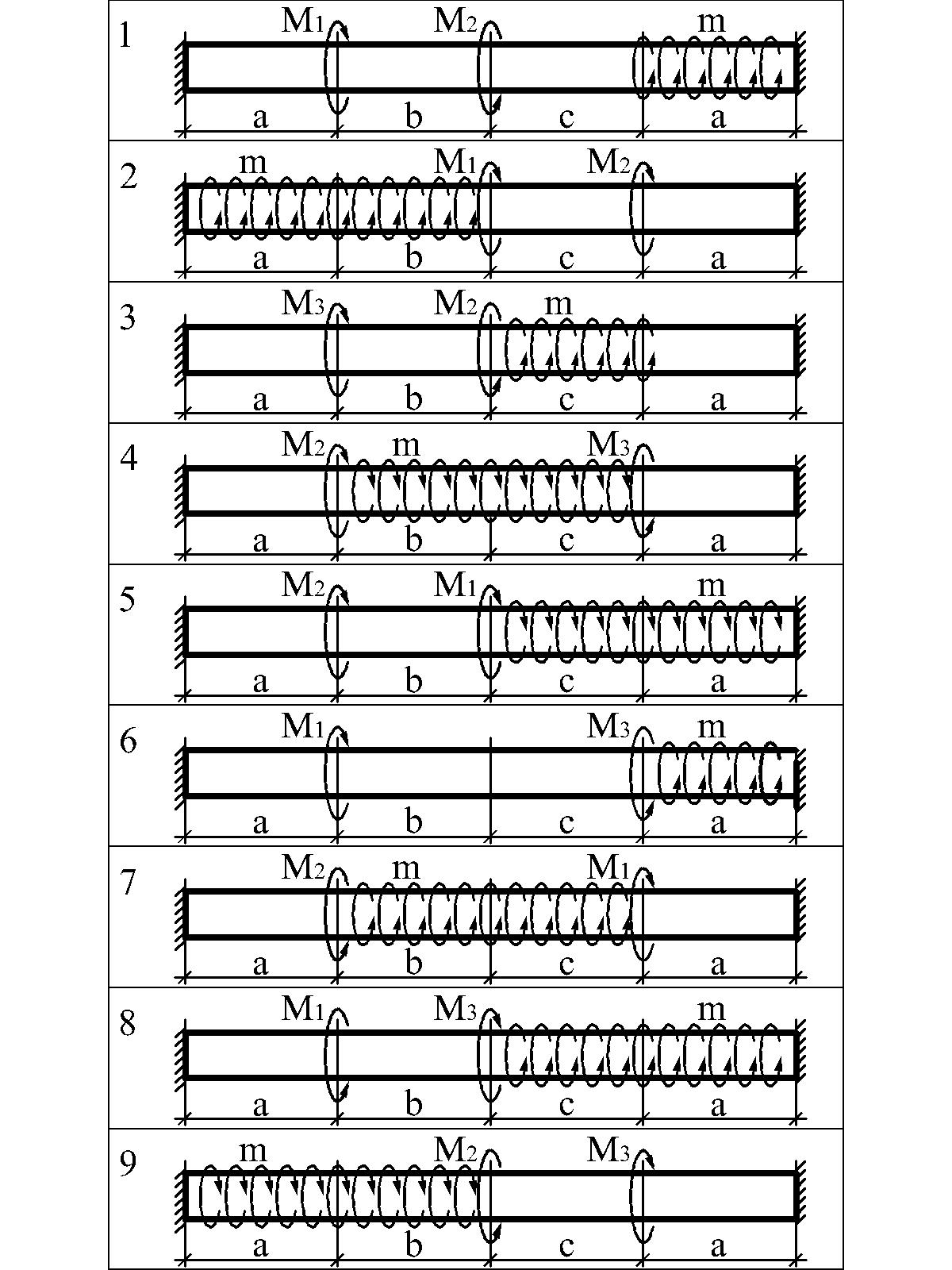
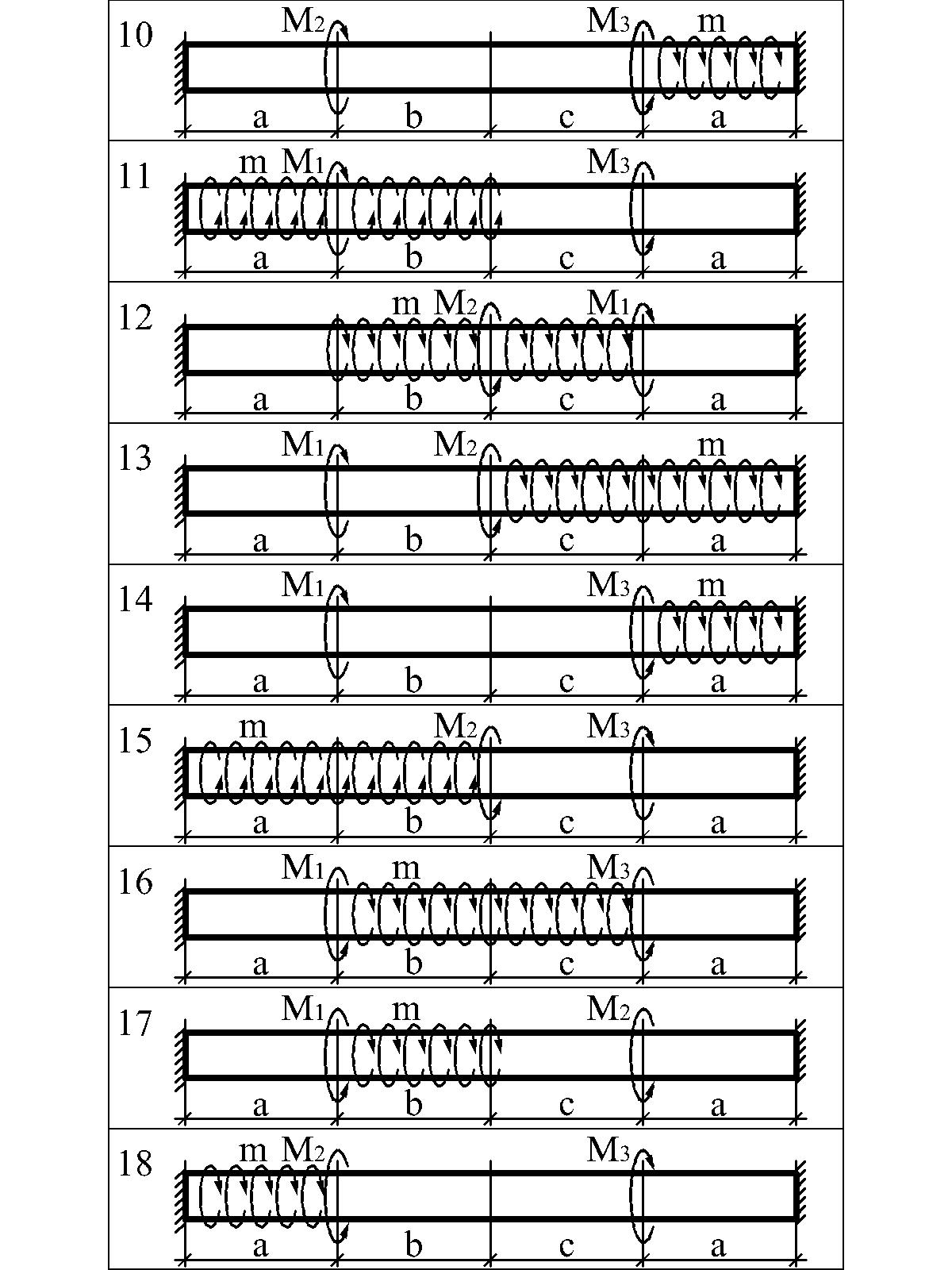
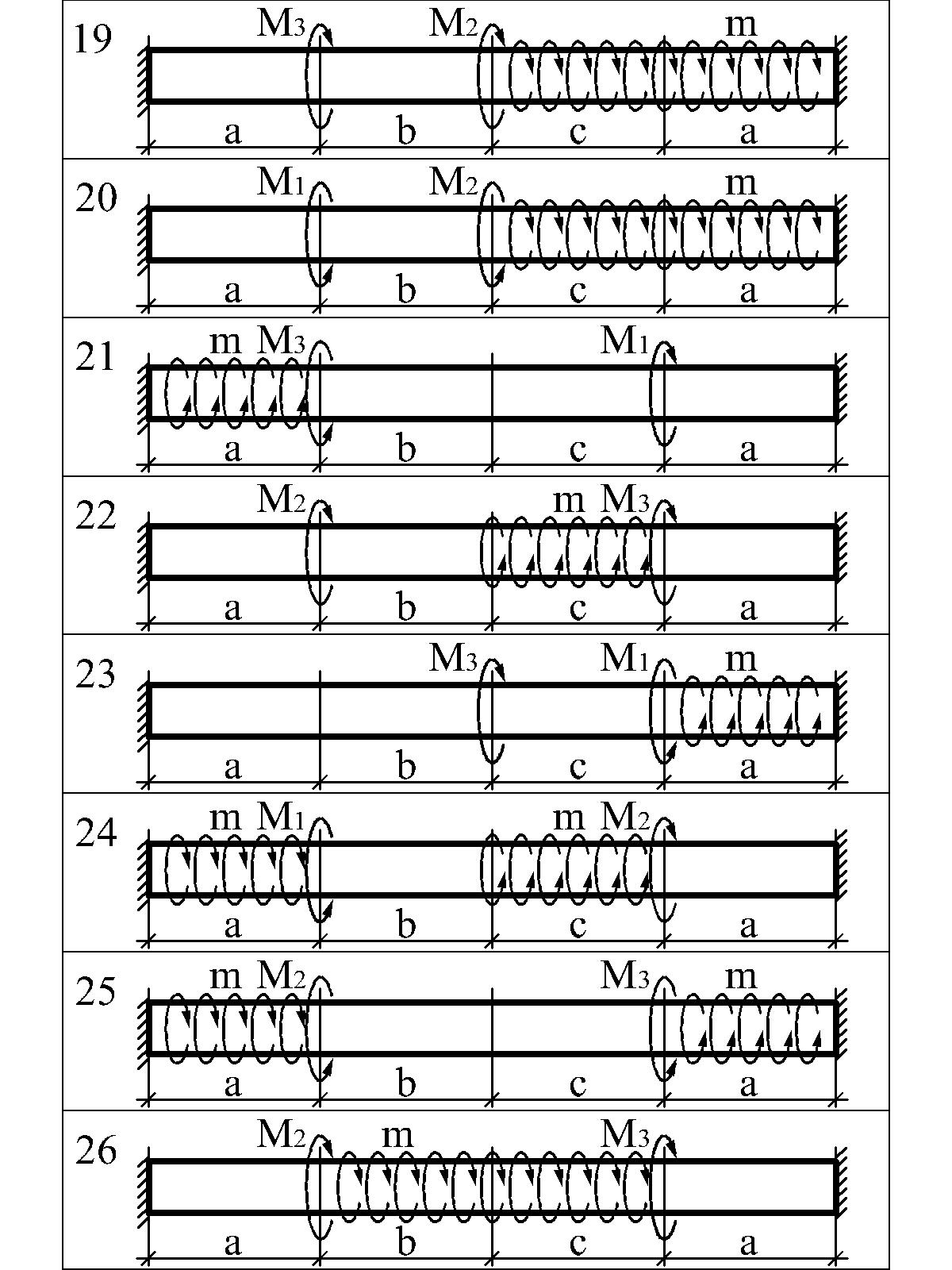
3.5. Индивидуальное задание 4 (контрольная работа 4). Прямой поперечный изгиб балок
3.5.1. Краткие сведения из теории
Прямым поперечным изгибом называется вид сопротивления материалов (вид деформации стержня), при котором внешние нагрузки действуют перпендикулярно оси стержня и находятся в плоскости, параллельной одной из главных осей инерции (или главной плоскости инерции) и проходящей через центр изгиба сечения. Центром изгиба называют особую точку в плоскости поперечного сечения стержня, которая характерна тем, что приложенная в ней нагрузка не вызывает в поперечном сечении крутящего момента (актуально для одиночного швеллера, уголка и подобных тонкостенных сечений).
При прямом поперечном изгибе в поперечном сечении возникают внутренние усилия: изгибающий момент M и поперечная сила Q. Для построения эпюр этих внутренних усилий стержень разбивается на грузовые участки. При помощи метода сечений определяются функции Mzi(x), Qyi(x), i = 1, …, n, где n – число участков, причем текущие координаты сечений могут определяться как в общей, так и в местных системах координат. На эпюре изгибающих моментов Mz знаки «+» и «–» принято не указывать, а откладывать значение «со стороны растянутых волокон».
Между Mz, Qy и q имеются следующие дифференциальные зависимости:
, 
, 
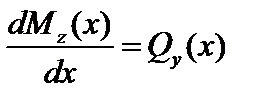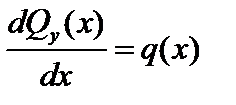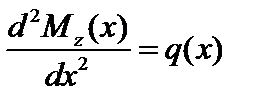. (3.28)