Для стержней прямоугольного сечения где – момент сопротивления при кручении; – коэффициент Сен-Венана; b, h > b – размеры прямоугольного сечения (рис. 3.10).
Условие расчета по несущей способности (условие прочности) записывается в виде:
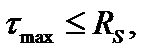 (3.24)
(3.24)
где Rs – расчетное сопротивление при сдвиге. При использовании 3-й теории прочности 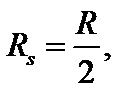 R – основное расчетное сопротивление.
R – основное расчетное сопротивление.
Условие (3.24) позволяет решать как поверочную, так и проектные задачи (проектирование сечений и нагрузок). В частности, при проектировании сечений используются следующие выражения: для круглого сечения 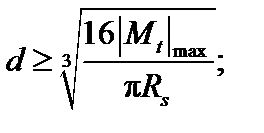 для кольцевого сечения
для кольцевого сечения 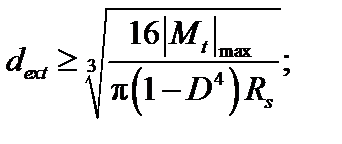 для прямоугольного сечения
для прямоугольного сечения 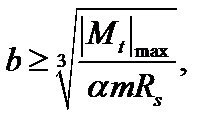 где
где 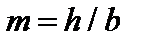 . Расчет по деформациям (на жесткость) заключается в проверке условия
. Расчет по деформациям (на жесткость) заключается в проверке условия
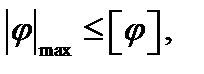 (3.25)
(3.25)
где 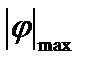 – максимальный по модулю угол закручивания сечения от нормативной нагрузки;
– максимальный по модулю угол закручивания сечения от нормативной нагрузки; 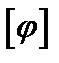 – допустимый угол закручивания.
– допустимый угол закручивания.
Величина 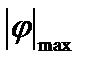 находится на основе анализа общего соотношения для углов закручивания на участках:
находится на основе анализа общего соотношения для углов закручивания на участках:
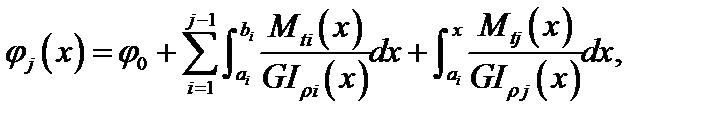
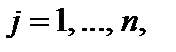 (3.26)
(3.26)
где 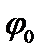 – угол закручивания начального сечения;
– угол закручивания начального сечения; 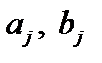 – координаты границ участка j.
– координаты границ участка j.
При кручении стержней прямоугольного сечения вместо 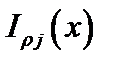 используется выражение
используется выражение 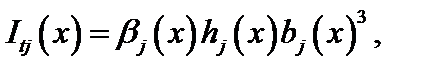 где
где 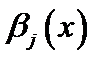 – коэффициент Сен-Венана. В рассматриваемых задачах
– коэффициент Сен-Венана. В рассматриваемых задачах 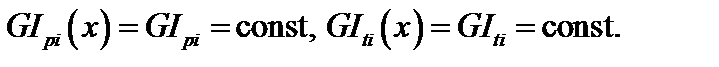
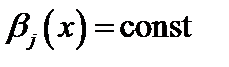 и т.д.
и т.д.
При кручении стержня, жестко защемленного по концам (правый конец стержня, приведенного на рис. 3.8, также защемлен), задача расчета является статически неопределимой. В таком случае для раскрытия статической неопределимости дополнительно к уравнению равновесия стержня 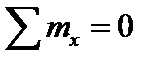 составляется уравнение
составляется уравнение 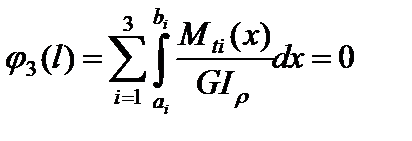 , вытекающее из рассмотрения геометрической и физической сторон задачи, а опорные реакции находятся из решения системы двух полученных уравнений.
, вытекающее из рассмотрения геометрической и физической сторон задачи, а опорные реакции находятся из решения системы двух полученных уравнений.
Расчет по предельной (разрушающей) нагрузке предполагает предварительное определение предельного крутящего момента 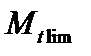 в сечении:
в сечении:
– для круглого стержня 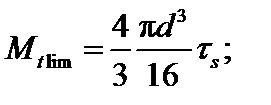
– для стержня кольцевого сечения 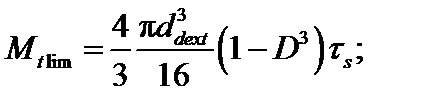
где 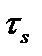 – предел текучести материала при сдвиге. В дальнейшем при однопараметрической нагрузке (все нагрузки выражаются через один параметр M (или m)) находится предельное значение
– предел текучести материала при сдвиге. В дальнейшем при однопараметрической нагрузке (все нагрузки выражаются через один параметр M (или m)) находится предельное значение 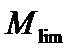 (или
(или 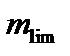 ) параметра нагрузки, при котором стержень либо всюду течет, либо превращается в механизм вследствие появления шарниров текучести. Условие расчета по предельной нагрузке имеет вид:
) параметра нагрузки, при котором стержень либо всюду течет, либо превращается в механизм вследствие появления шарниров текучести. Условие расчета по предельной нагрузке имеет вид:
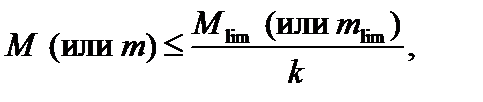 (3.27)
(3.27)
где M (или m) – заданная величина параметра нагрузки; k – коэффициент запаса прочности по нагрузке, k > 1.
3.4.2. Задача 3.1
Варианты поперечных сечений приведены на рис. 3.11, расчетные схемы стержней для статической определимой задачи 3.1 при кручении даны ниже. Варианты остальных исходных данных по задаче 3.1 представлены в табл. 3.1.
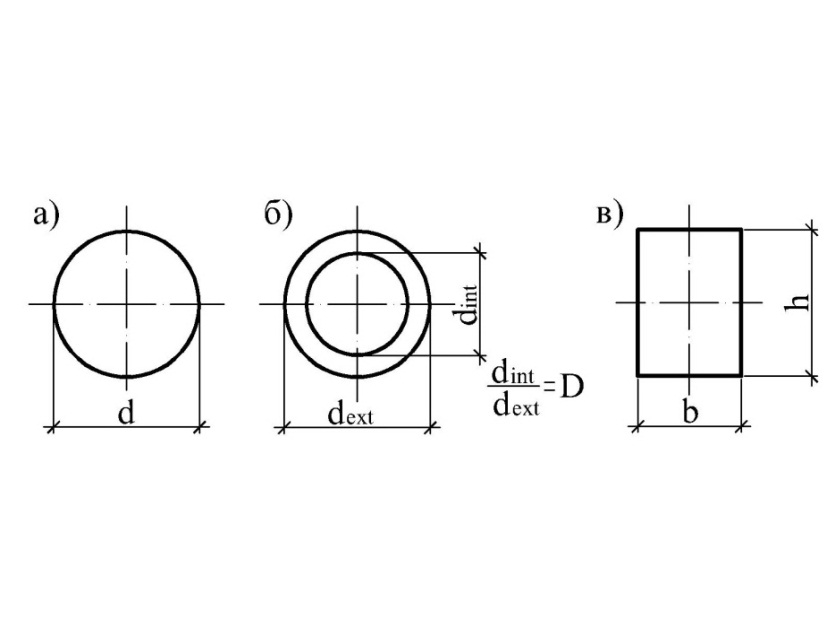
Рис. 3.11
Значения коэффициентов Сен-Венана α, β, γ приведены в табл. П.2.
Требуется:
1. Построить эпюру крутящих моментов в сечении стержня.
2. По условию прочности подобрать сечение стержня в вариантах а, б, в (см. рис. 3.11).
3. Построить эпюру углов закручивания сечения при постоянной жесткости стержня. 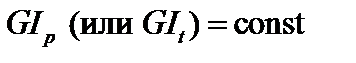 .
.
4. Подобрать сечение из условия жесткости (вариант б, 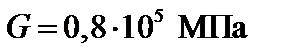 ).
).
5. Выбрать окончательные размеры сечения (вариант б) из условий прочности и жесткости.
Таблица 3.1
| Вид исходных данных | Варианты исходных данных к задаче 3.1 | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| a, м | 1,2 | 1,1 | 1,0 | 1,2 | 0,8 | 1,3 | 0,7 | 1,2 | 0,8 | 1,1 |
| b, м | 0,8 | 1,3 | 1,4 | 1,0 | 1,1 | 0,7 | 1,2 | 0,9 | 1,1 | 0,7 |
| c, м | 1,0 | 0,7 | 0,8 | 0,7 | 1,2 | 0,9 | 1,3 | 1,1 | 1,4 | 1,5 |
| М1, кН·м | 2,1 | 1,8 | 2,3 | 1,9 | 1,6 | 1,8 | 2,3 | 2,2 | 1,9 | 2,1 |
| М2, кН·м | 1,8 | 2,2 | 1,4 | 2,5 | 2,6 | 1,5 | 1,2 | 1,4 | 2,1 | 1,4 |
| М3, кН·м | 1,9 | 1,6 | 1,8 | 1,3 | 1,2 | 2,1 | 1,6 | 1,8 | 1,6 | 1,8 |
| m, Н·м/м | 1,0 | 1,2 | 1,3 | 1,1 | 0,8 | 1,4 | 1,2 | 1,0 | 1,3 | 1,5 |
| h/b | 1,2 | 1,5 | 3,0 | 2,0 | 4,0 | 1,5 | 2,0 | 1,1 | 4,0 | 3,0 |
| D | 0,9 | 0,85 | 0,8 | 0,75 | 0,8 | 0,85 | 0,9 | 0,85 | 0,8 | 0,75 |
| Rs, МПа | 100 | 90 | 80 | 70 | 60 | 70 | 80 | 90 | 100 | 80 |
| [φ], рад | 0,03 | 0,04 | 0,05 | 0,06 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,05 |








