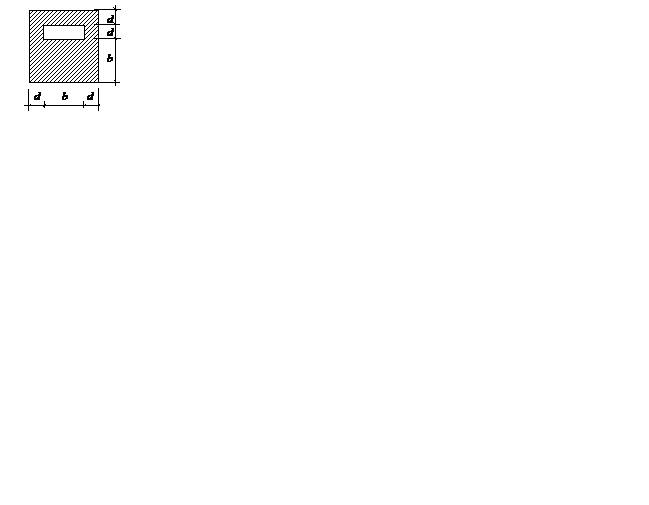
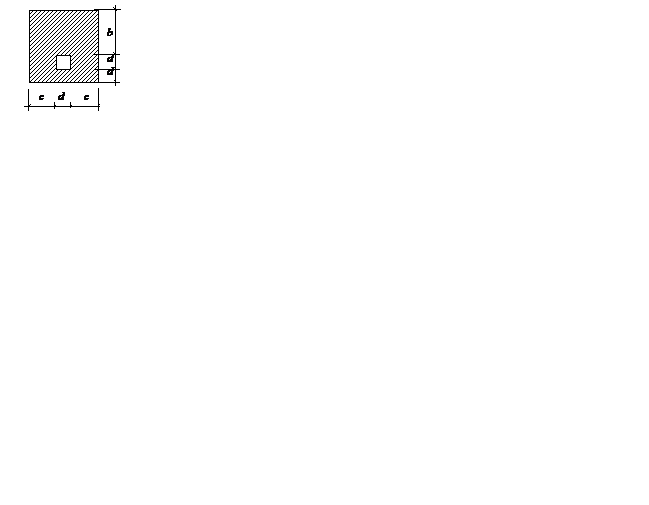
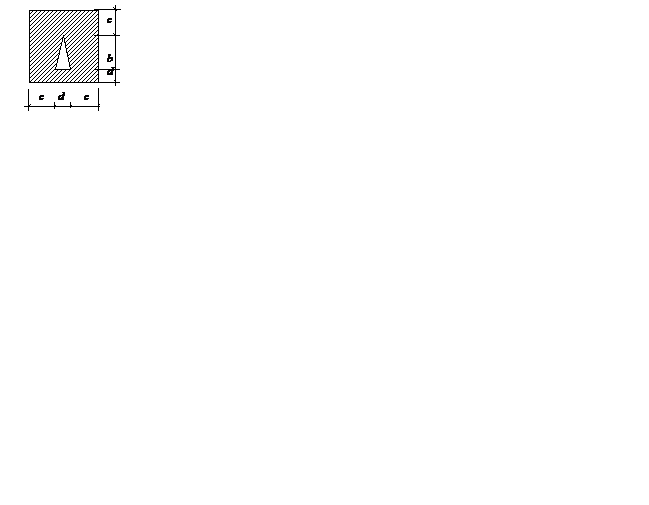
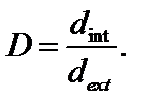Варианты поперечных сечений к задаче 2.2
1
| 2
| 3
|
| 4
| 5
| 6
|
| 7
| 8
| 9
|
| 10
| 11
| 12
|
| 13
| 14
| 15
|
| 16
| 17
| 18
|
| 19
| 20
| 21
|
| 22
| 23
| 24
|
3.3.4. Задача 2.3. Определение геометрических характеристик плоских сечений
Дано поперечное сечение стержня (см. варианты поперечных сечений к задаче 2.3).
Требуется:
1. Начертить заданное поперечное сечение в масштабе, проставить размеры в сантиметрах.
2. Определить координаты центра тяжести сечения и провести горизонтальную и вертикальную центральные оси.
3. Определить осевые и центробежный моменты инерции сечения относительно проведенных центральных осей.
4. Определить положение главных центральных осей инерции и показать их на чертеже.
5. Вычислить величины главных центральных моментов инерции.
6. Определить величины главных центральных радиусов инерции сечения.
Таблица 2.3
| Вид исходных данных | Варианты исходных данных к задаче 2.3 | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Прямоугольник | 10×1 | 10×2 | 12×1 | 20×2 | 12×4 | 16×1 | 16×2 | 36×4 | 20×2 | 24×4 |
| Номер двутавра | 12 | 14 | 18 | 20 | 24 | 30 | 36 | 22 | 40 | 36 |
| Номер швеллера | 16 | 18 | 20 | 22 | 27 | 18а | 30 | 24 | 36 | 33 |
| Номер равнополочного уголка / толщина, мм | 4/4 | 5/4 | 7/5 | 5/6 | 8/6 | 8/8 | 10/8 | 14/10 | 16/12 | 10/12 |
| Номер неравнополочного уголка / размеры, см | 5/3,2 | 4/3 | 8/5 | 11/7 | 12,5/8 | 12,5/8 | 14/9 | 16/10 | 16/10 | 14/9 |
| Толщина, мм | 4 | 5 | 5 | 8 | 8 | 10 | 8 | 10 | 12 | 10 |
Варианты поперечных сечений к задаче 2.3
| 1
| 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 10 | 11 | 12 |
| 13 | 14 | 15 |
| 16 | 17 | 18 |
| 19 | 20 | 21 |
| 22 | 23 | 24 |
3.4. Индивидуальное задание 3 (контрольная работа 3). Расчет прямых стержней при деформации кручения
3.4.1. Краткие сведения из теории
Кручением называется деформация прямого стержня при действии внешней нагрузки в виде пар сил, плоскости которых перпендикулярны продольной оси стержня (рис. 3.8).
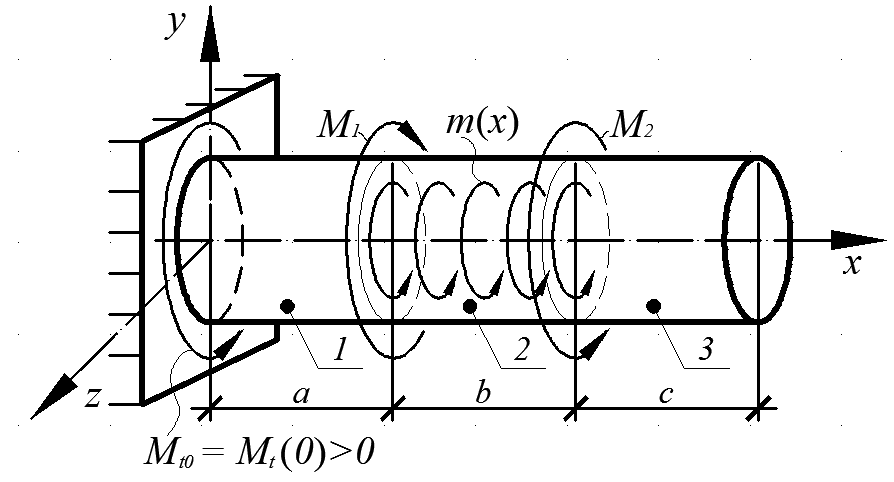
Рис. 3.8
В данном случае силы внутреннего взаимодействия между частицами в поперечном сечении суммируются к одному усилию – крутящему моменту Mt. При построении эпюры Mt стержень разбивается на участки, и с помощью метода сечений определяются функции Mti(x), i = 1, ..., n, где n – число участков. Например, для случая, приведенного на рис. 3.8, n = 3,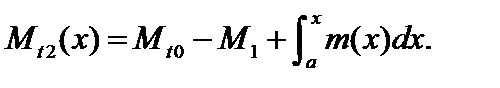 
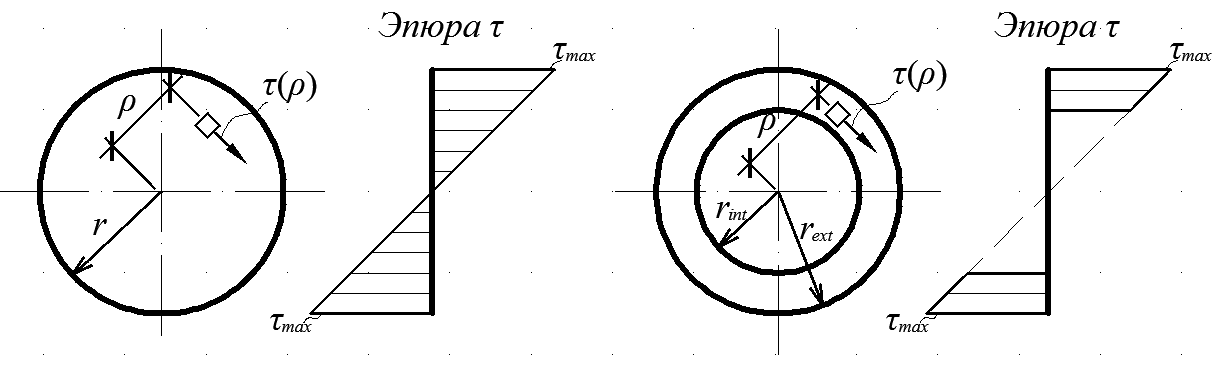
При свободном кручении стержней в поперечном сечении возникают только касательные напряжения. Для стержней круглого и кольцевого сечения (рис. 3.9) выражение для касательных напряжений имеет вид:
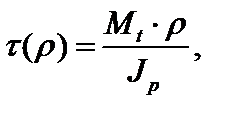(3.23)
где Iρ – полярный момент инерции.
| а) | б) |
|
| |
Рис. 3.9: а – круглое сечение; б – кольцевое сечение
Величина максимальных касательных напряжений в сечении равна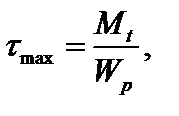 
где Wρ – полярный момент сопротивления сечения. Для круглого сечения 
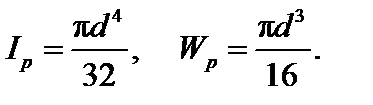Для кольцевого сечения 
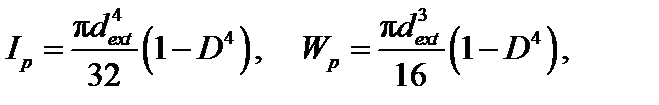где 