Геометрические характеристики сечений
Основными геометрическими характеристиками сечения являются (рис. 3.5):
· площадь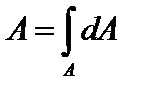 
;
· статические моменты площади сечения относительно осей z, y
, 
;
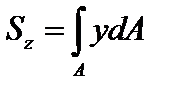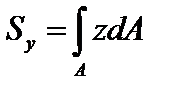· осевые моменты инерции относительно осей z, y
, 
;
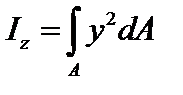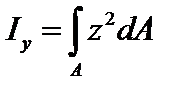· центробежный момент инерции относительно осей z, y
.
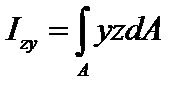Для основных типов сечений выражения для определения их геометрических характеристик представлены ниже в форме таблицы.
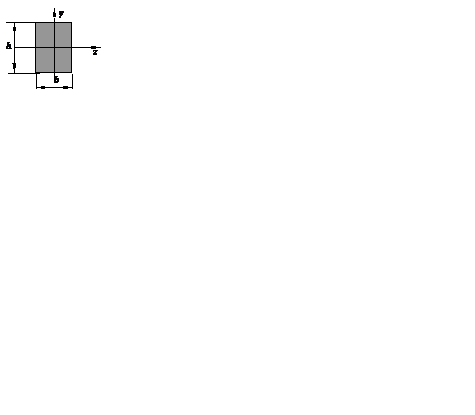
Прямоугольник
 ,  , 
| 
|
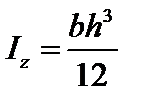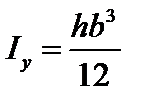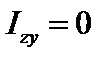
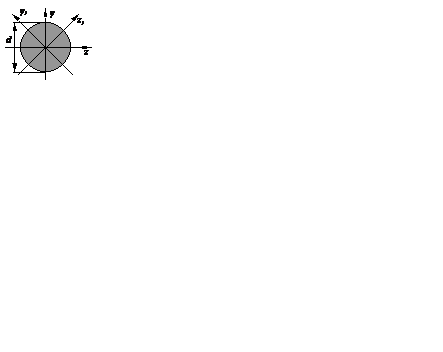
Круг
 ,
 ,
| 
|
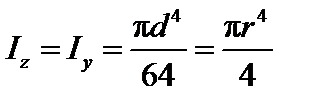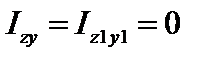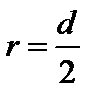
Кольцо
| 
|
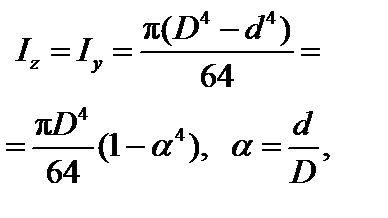
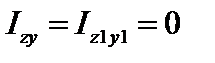
Полукруг
 ,  , 
| |
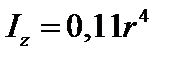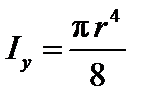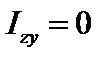
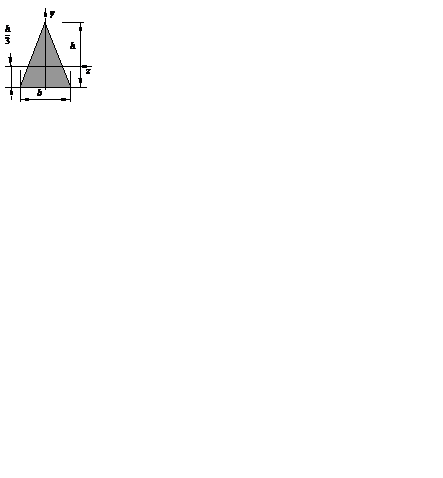
Треугольник
равнобедренный
 ,  , 
| 
|
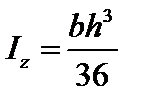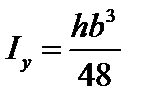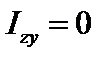
Главными осями инерции сечения называются взаимно-перпендикулярные оси, относительно которых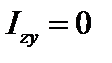 
.
Координаты центра тяжести составного сечения относительно произвольных осей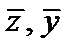 
определяются по формулам
, 
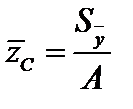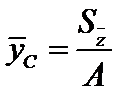. (3.17)
Центральными осями сечения называются все оси, проходящие через центр тяжести сечения. Относительно центральных осей статические моменты сечения равны нулю.
| Рис. 3.6 |
Для определения главных центральных моментов инерции составного сечения удобно использовать формулы перехода при параллельном переносе осей (см. рис. 3.5):
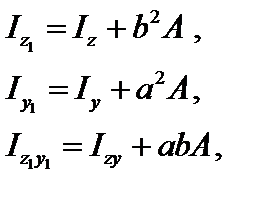(3.18)
а также зависимость между моментами инерции при повороте осей на угол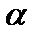 
(рис. 3.6)
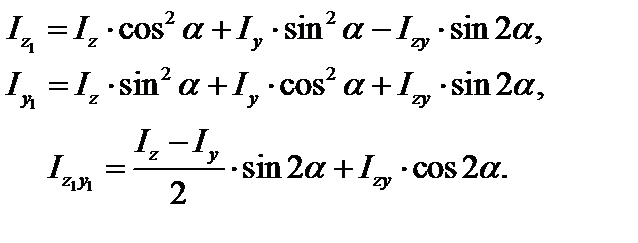(3.19)
Главные центральные моменты инерции можно определить, используя следующие выражения:
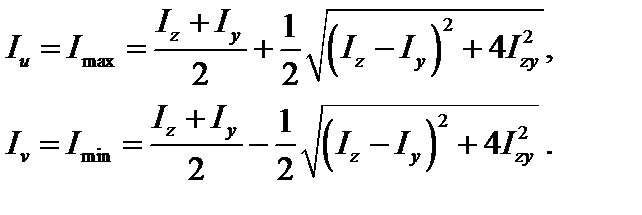(3.20)
Направления главных осей определяются по формулам
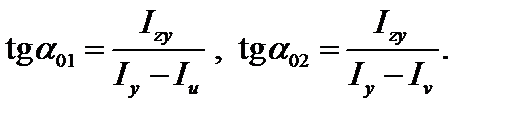(3.21)
Радиусы инерции сечения определяются по формулам
, 
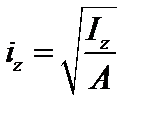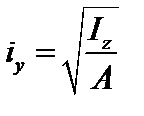. (3.22)
3.3.2. Задача 2.1. Плоское напряженное состояние
Дано: на площадках рассматриваемого элемента объема заданы напряжения (рис. 3.7). Варианты остальных исходных данных приведены в табл. 2.1. Выбор номера варианта аналогичен выбору номера расчетной схемы (см. с. 14).
Требуется:
1. Выполнить чертеж с учетом знака напряжений.
2. Определить главные напряжения и положение главных площадок.
3. Найти экстремальные касательные напряжения и положение соответствующих им площадок.
4. Найти деформации в направлении заданных осей x, y и главные деформации.
5. Проверить выполнение условий прочности по различным теориям прочности: 1) теория максимальных нормальных напряжений; 2) теория наибольших линейных деформаций; 3) теория максимальных касательных напряжений; 4) энергетическая теория; 5) теория прочности Кулона–Мора.
Таблица 2.1
| № вар. | s x | s y | t xy | Материал | № вар. | s x | s y | t xy | Материал |
| 1 | 30 | 80 | 60 | Медь | 26 | 90 | 80 | 60 | Сталь |
| 2 | 40 | –50 | 70 | 27 | 140 | 80 | 60 | ||
| 3 | 70 | –30 | 50 | 28 | 90 | 110 | 50 | ||
| 4 | 60 | 20 | 40 | 29 | 60 | –90 | 40 | ||
| 5 | 70 | 20 | –50 | 30 | 140 | 80 | 50 | ||
| 6 | 30 | –40 | 50 | Алюминий | 31 | –100 | 70 | 50 | Сталь |
| 7 | –20 | –30 | 50 | 32 | –90 | 90 | 50 | ||
| 8 | –50 | 20 | 60 | 33 | 80 | 100 | –60 | ||
| 9 | –40 | 40 | 50 | 34 | 170 | –60 | 50 | ||
| 10 | 50 | –20 | 30 | 35 | 60 | 90 | –30 | ||
| 11 | 140 | –70 | 20 | Сталь | 36 | 80 | –70 | 20 | Серый чугун |
| 12 | –80 | –60 | 40 | 37 | 20 | –60 | 40 | ||
| 13 | 80 | 130 | 50 | 38 | 80 | 60 | 50 | ||
| 14 | 75 | –120 | 60 | 39 | 90 | 80 | 60 | ||
| 15 | 10 | 100 | 40 | 40 | –10 | 40 | 60 | ||
| 16 | 90 | 20 | 30 | Серый чугун | 41 | 90 | 20 | –90 | Сталь |
| 17 | –80 | 60 | 50 | 42 | 130 | –60 | 50 | ||
| 18 | 20 | 40 | 60 | 43 | –90 | 100 | 60 | ||
| 19 | 90 | –40 | 70 | 44 | 110 | –40 | 30 | ||
| 20 | 60 | 80 | 80 | 45 | –60 | –100 | 80 | ||
| 21 | –30 | –80 | 60 | Сосна | 46 | 70 | 120 | –60 | Сталь |
| 22 | –60 | –50 | 50 | 47 | 60 | –130 | 50 | ||
| 23 | –70 | –50 | 50 | 48 | –70 | 160 | –50 | ||
| 24 | 10 | –90 | 40 | 49 | 100 | –120 | 20 | ||
| 25 | –50 | –30 | 40 | 50 | –90 | 110 | 10 |
Расчетные сопротивления материалов, модули упругости и коэффициенты Пуассона приведены в табл. П.1.
3.3.3. Задача 2.2.Определение геометрических характеристик плоских сечений
Дано поперечное сечение стержня (см. варианты поперечных сечений к задаче 2.2).
Требуется:
1. Начертить заданное поперечное сечение в масштабе, проставить размеры в сантиметрах.
2. Определить координаты центра тяжести сечения и провести главные центральные оси.
3. Определить величины главных центральных моментов инерции.
4. Определить величины главных центральных радиусов инерции сечения.
Таблица 2.2
| Вид исходных данных | Варианты исходных данных к задаче 2.2 | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| a | 24 | 20 | 36 | 20 | 20 | 32 | 24 | 18 | 40 | 48 |
| b | 12 | 10 | 24 | 12 | 16 | 20 | 18 | 16 | 36 | 32 |
| c | 8 | 6 | 12 | 8 | 12 | 12 | 10 | 8 | 24 | 20 |
| d | 4 | 3 | 4 | 2 | 4 | 4 | 2 | 4 | 6 | 8 |