Статически неопределимые системы при растяжении-сжатии и порядок их расчета
Системы, для определения реакций в связях которых недостаточно уравнений равновесия (уравнений статики), называются статически неопределимыми. Примеры статически неопределимых стержневых систем с растянутыми (сжатыми) элементами показаны на рис. 3.4.
а) б) в)
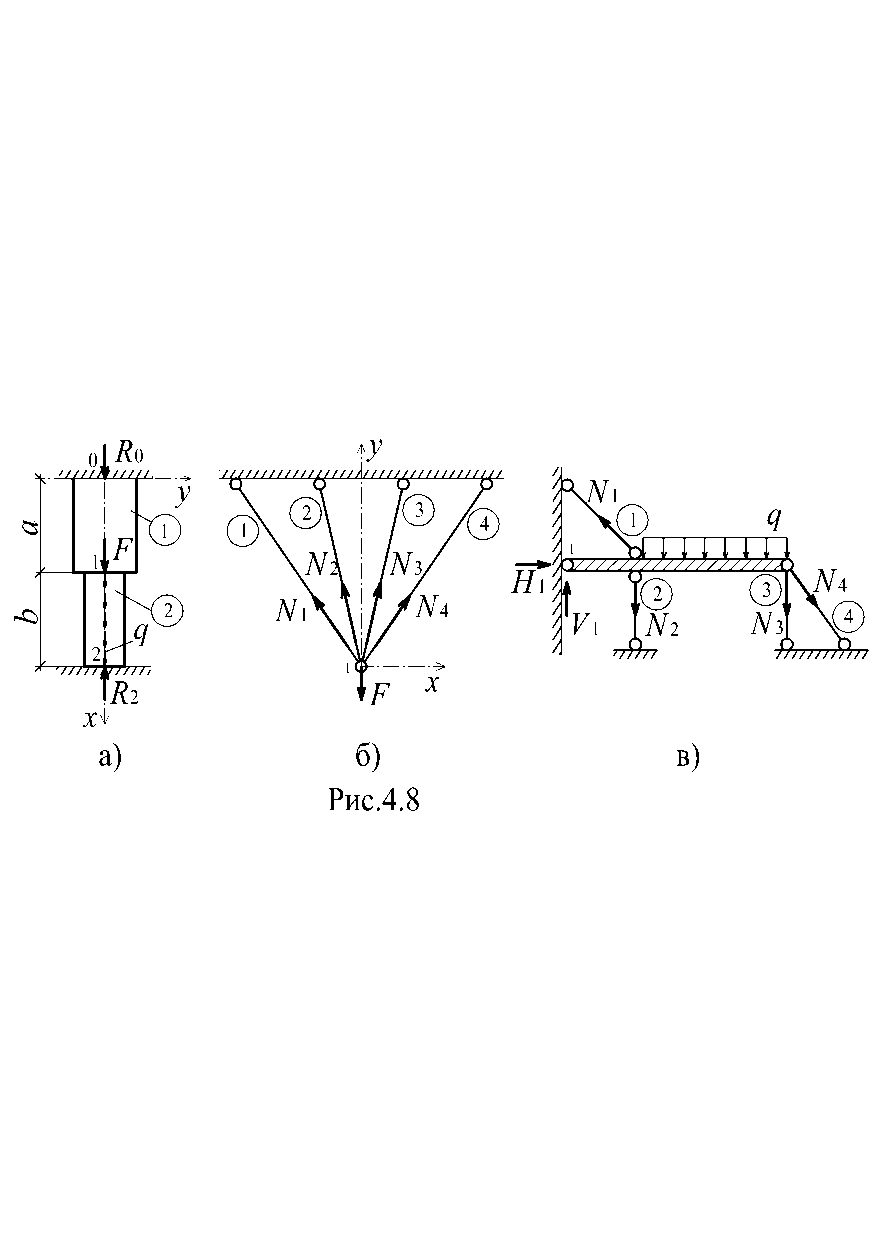
Рис. 3.4
Пользуясь методом сечений, нетрудно убедиться, что во всех показанных на рис. 3.4 случаях для определения реакций в связях систем недостаточно уравнений равновесия. Для получения недостающих уравнений необходимо, кроме статической, рассмотреть две другие стороны задачи – геометрическую и физическую. Подробнее методика расчета статически неопределимых систем при растяжении-сжатии изложена в [6] и в п. 4.1 данного пособия.
Расчет стержней при растяжении сжатии по предельным состояниям
В рассматриваемом случае условие расчета по несущей способности (прочности) для участка стержня, выполненного из материала с единым расчетным сопротивлением при растяжении и сжатии, записывается следующим образом:
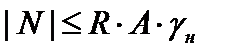 , (3.8)
, (3.8)
где N – продольная сила в опасном сечении, зависящая от составляющих вектора расчетных нагрузок на стержень; A – площадь опасного сечения; R – расчетное сопротивление материала; 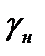 – коэффициент надежности по назначению конструкции, который в дальнейшем будет считаться равным единице.
– коэффициент надежности по назначению конструкции, который в дальнейшем будет считаться равным единице.
В качестве условий жесткости (условий расчета по деформациям) в данном случае используются следующие:
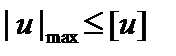 ;
; 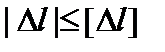 , (3.9)
, (3.9)
где |u|max – максимальное по абсолютной величине продольное перемещение одного из сечений стержня; |Dl| – абсолютная деформация всего стержня, или отдельного его участка; [u], [Dl] – допускаемые значения рассматриваемых характеристик деформации стержня.
Величины |u|max и |Dl| вычисляются при действии нормативных нагрузок.
Условия (3.8), (3.9) позволяют решать три типа задач:
– поверочная задача;
– проектная задача 1 – подбор сечений стержня;
– проектная задача 2 – подбор параметра нагрузки на стержень.
В том случае, когда стержень выполнен из материалов с различными значениями расчетных сопротивлений, условия вида (3.8) составляются по каждому из материалов.
Для материалов с различными расчетными сопротивлениями при растяжении и при сжатии условия вида (3.8) составляются отдельно для опасных сечений по растяжению и сжатию:
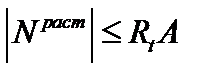 ;
; 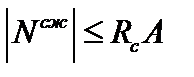 . (3.10)
. (3.10)
Расчет по разрушающим (предельным) нагрузкам
Идея метода расчета конструкций по разрушающим (предельным) нагрузкам основана на предварительном выявлении параметра разрушающей (предельной) нагрузки 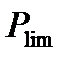 . Условие надежной работы конструкции записывается в следующем виде:
. Условие надежной работы конструкции записывается в следующем виде:
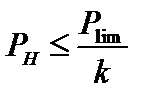 , (3.11)
, (3.11)
где РН – параметр заданной нагрузки; k – коэффициент запаса прочности по нагрузке, учитывающий все факторы, снижающие надежность работы конструкции, k > 1.
Применение метода разрушающих нагрузок имеет смысл прежде всего для пластичных материалов. При определении предельной нагрузки в качестве предельных значений напряжений принимаются пределы текучести материала (материалов) стержня. При этом предельным будет такое состояние конструкции, при котором материалы либо всюду текут, либо конструкция в результате локальной текучести превращается в механизм. В случае статически неопределимых систем использование метода расчета по разрушающим (предельным) нагрузкам позволяет экономить материал при одинаковых коэффициентах запаса прочности по напряжениям и нагрузке.
3.2.2. Задача 1.1. Статически определимая система
Дано: стойка из бетона жестко закреплена на нижнем конце и нагружена силами F1, F2 и q, действующими вдоль оси стержня.
Е = 0,27  105 МПа, Rc = 12 МПа, Rt = 0,9 МПа.
105 МПа, Rc = 12 МПа, Rt = 0,9 МПа.
Требуется:
1. Построить эпюру продольных сил N.
2. Определить требуемые площади поперечных сечений из условий прочности и соблюдения при этом заданного соотношения площадей на различных участках.
3. Построить эпюру нормальных напряжений σ.
4. Построить эпюру перемещений сечений u.
5. Выполнить проверку жесткости. [Δl] = (0,01–0,02)l, [u] = = 0,001 l. Здесь l – длина стержня.
Таблица 1.1
| Вид исходных данных | Варианты исходных данных к задаче 1.1 | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| a, м | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 |
| F1, кН | 100 | 110 | 140 | 80 | 160 | 140 | 150 | 120 | 80 | 100 |
| F2, кН | 120 | 100 | 120 | 110 | 120 | 110 | 180 | 150 | 60 | 110 |
| F3, кН | 130 | 120 | 80 | 140 | 100 | 150 | 160 | 160 | 40 | 150 |
| q, кН/м | 20 | 40 | 60 | 40 | 50 | 60 | 80 | 40 | 20 | 60 |
Варианты расчетных схем к задаче 1.1
        
|
        
|
        
| |||
|
        
|
        
|
| |||
|
        
|
         
|
         
| |||
         
|
        
|
       
| |||
        
|
         
|
        
| |||
        
|
         
|
        
| |||
        
|
         
|
        
| |||

       
|
         
|
        
|
3.2.3. Задача 1.2. Статически неопределимая система
Дано: составной стержень из алюминиевых и стальных частей жестко закреплен на нижнем конце и нагружен силами F1, F2 и q, действующими вдоль оси стержня.
Для алюминия Еа = 0,7.105 МПа, αа = 23.10–6 1/град.
Для стали Ес = 2,1.105 МПа, αс = 13.10–6 1/град.
Исходные данные взять из табл. 1.2.
Требуется:
1. Определить опорные реакции при действии сил F1, F2, и q, увеличении температуры на Δt и при наличии монтажного зазора между верхним концом бруса и опорой величиной  = 1 мм.
= 1 мм.
2. Построить эпюры продольных сил N, нормальных напряжений σ и перемещений u. Принять параметр площади поперечного сечения А = 20 см2.
Таблица 1.2
| Вид исходных данных | Варианты исходных данных к задаче 1.2 | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| a, м | 4 | 2 | 3 | 4 | 2 | 3 | 4 | 2 | 3 | 4 |
| F1, кН | 100 | 110 | 140 | 80 | 160 | 140 | 150 | 120 | 80 | 100 |
| F2, кН | 120 | 100 | 120 | 110 | 120 | 110 | 180 | 150 | 60 | 110 |
| q, кН/м | 70 | 40 | 60 | 40 | 50 | 60 | 80 | 40 | 70 | 60 |
| Δtо | 100 | 90 | 80 | 60 | 120 | 110 | 60 | 80 | 90 | 100 |
Варианты расчетных схем к задаче 1.2
|
        
|
                 
|
        
        
| ||||||||||||||
|
        
|
         
|
        
| ||||||||||||||
|
        
|
         
|

| ||||||||||||||
|
       
|
          
|
        
| ||||||||||||||
|
        
|
         
|
        
| ||||||||||||||
        
|
         
|
        
| ||||||||||||||
        
|
         
|
        
| ||||||||||||||
        
|
         
|
         
| ||||||||||||||
3.2.4. Задача 1.3. Статически неопределимая стержневая система
Дано: жесткий стержень, нагруженный силой F, закреплен с помощью шарнирно-неподвижной опоры и двух стержней. Материал стержней – сталь.
Исходные данные взять из табл. 1.3.
Требуется:
1. Определить усилия в стержнях при действии силы F.
2. Определить параметр площади поперечного сечения А из условия прочности R = 200 МПа.
3. Найти значение нагрузки Fs по методу предельного равновесия и допустимое значение силы Fadm. Сравнить Fadm с заданной нагрузкой. Принять предел текучести σ s = 240 МПа, коэффициент запаса прочности k = 1,2.
Таблица 1.3
| Вид исходных данных | Варианты исходных данных к задаче 1.3 | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| a, м | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 |
| F, кН | 40 | 50 | 60 | 70 | 80 | 90 | 40 | 50 | 60 | 80 |
Варианты расчетных схем к задаче 1.3
|
|
|
| ||||
|
     
|
     
|
     
| ||||
|
|
| |||||
|
       
|
| |||||
|
     
|
     
| |||||
|
|
| |||||
|
      
|
| |||||
|
|
     
| |||||
|
|
       
| |||||
|
     
|
| |||||
|
|
| |||||
3.3. Индивидуальное задание 2 (контрольная работа 2). Напряженно-деформированное состояние материала в точке. Геометрические характеристики сечений
3.3.1. Краткие сведения из теории
Напряженным состоянием в точке называется совокупность напряжений на множестве площадок, проходящих через данную точку.
Правила знаков: растягивающие нормальные напряжения считаются положительными, сжимающие – отрицательными;
Главными называются площадки, на которых касательные напряжения равны нулю, соответствующие этим площадкам нормальные напряжения также называются главными. Принята следующая индексация главных напряжений:
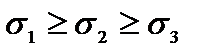 . (3.12)
. (3.12)
Определение главных напряжений в случае плоского напряженного состояния:
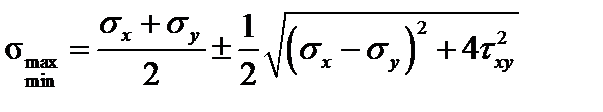 . (3.13)
. (3.13)
Определение положения главных площадок:
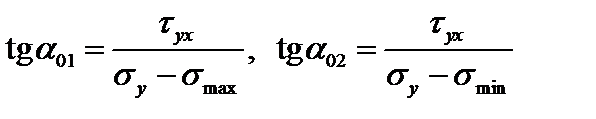 . (3.14)
. (3.14)
Максимальные касательные напряжения определяются по формуле
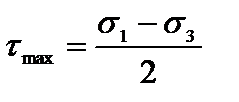 . (3.15)
. (3.15)
Линейные и угловые деформации определяются с использованием обобщенного закона Гука:
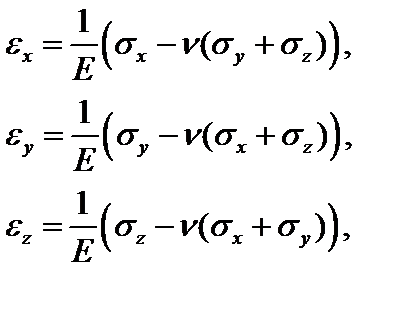
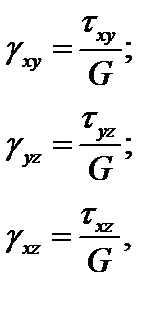 (3.16)
(3.16)
где 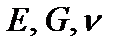 – модуль упругости, модуль сдвига и коэффициент Пуассона материала соответственно, для расчетов нужно выбрать их значения из табл. П.1 (приложение).
– модуль упругости, модуль сдвига и коэффициент Пуассона материала соответственно, для расчетов нужно выбрать их значения из табл. П.1 (приложение).
Классические теории прочности
| Первая теория прочности (используется при линейном напряженном состоянии) | Для пластичного материала 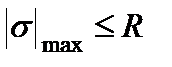 . Для хрупкого материала . Для хрупкого материала
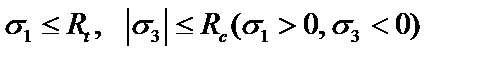
|
| Вторая теория прочности | 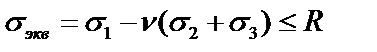
|
| Третья теория прочности | 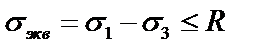
|
| Четвертая (энергетическая) теория прочности (используется для пластичных материалов) | 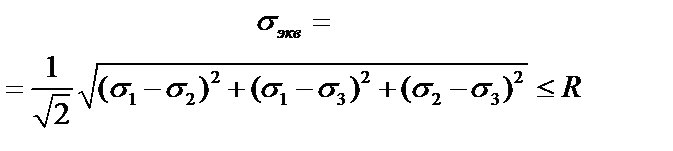
|
| Теория прочности Кулона–Мора (используется для хрупких материалов) | 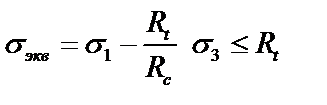 ,
где ,
где 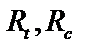 – расчетные сопротивления материала при растяжении и сжатии – расчетные сопротивления материала при растяжении и сжатии
|




















