Определение напряжений и деформаций в точках поперечных сечений

Дата: 2025-05-25; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Нормальные напряжения равномерно распределяются по площади поперечного сечения: 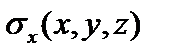= 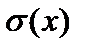, – а их величина в произвольном поперечном сечении определяется согласно соотношению

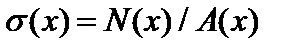, (3.1)

где 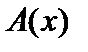– площадь поперечного сечения стержня.

Полагая, что справедлив закон Гука и закон линейного температурного деформирования, получим соотношение для линейной деформации в продольном направлении:

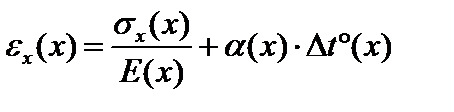, (3.2)

где 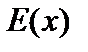, , 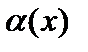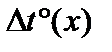– функции, определяющие модуль упругости, коэффициент температурной деформации и изменение температуры в сечениях стержня. Как правило, эти функции задаются кусочно-постоянными на участках стержня. В рассматриваемой постановке также считается, что они не зависят от координат точки сечения, т.е. постоянны в рассматриваемом поперечном сечении.

Определение абсолютной деформации стержня и перемещений поперечных сечений

Рассмотрим прямой стержень, нагруженный силовой и температурной нагрузками и состоящий из n участков (рис. 3.2). Под участком i, i = 1, …, n, будем в данном случае понимать такую протяженность стержня, на которой функция

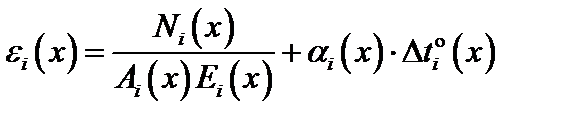
не меняется.

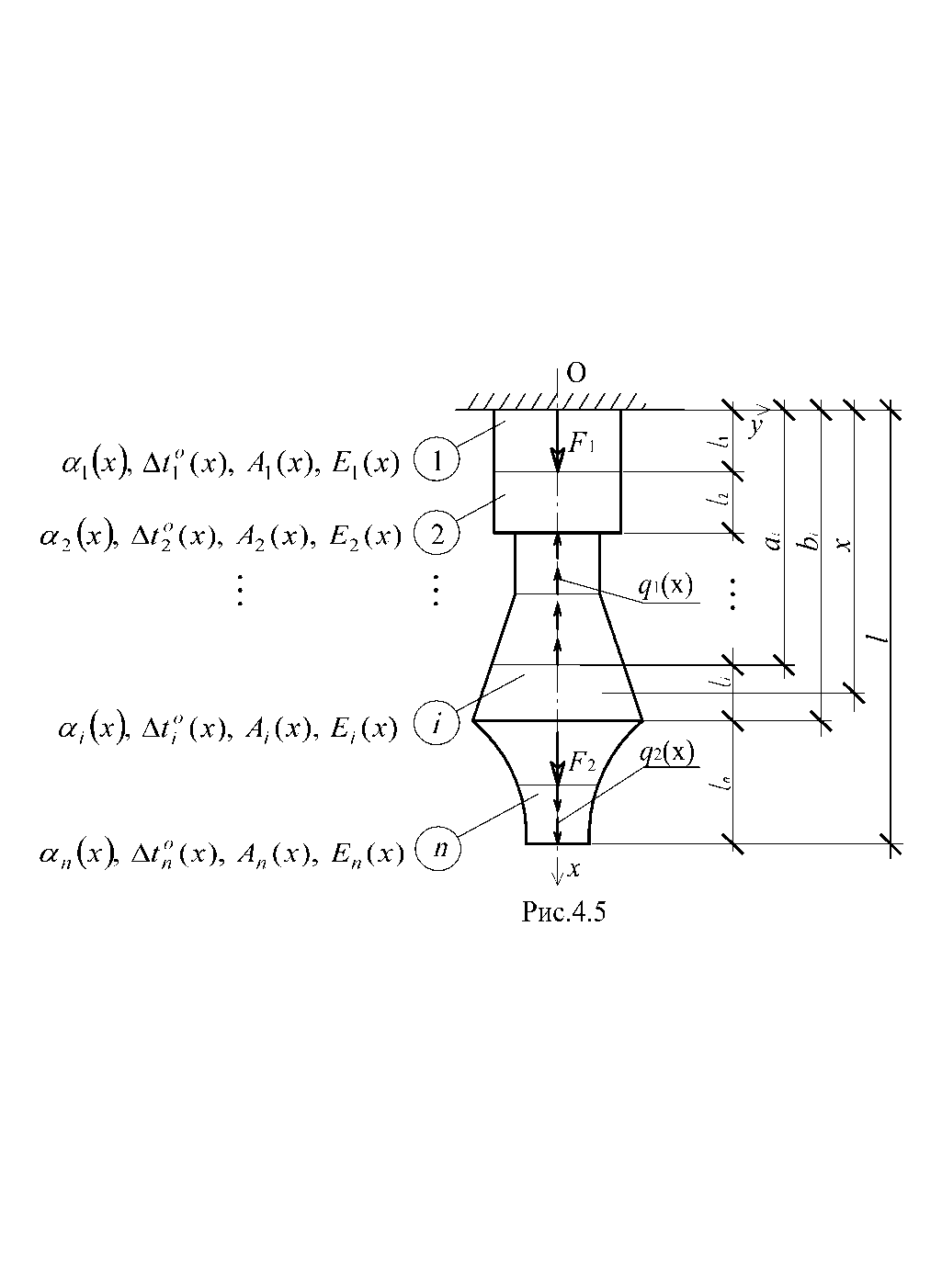
Рис. 3.2

Суммируя деформации элементарных частей стержня на участке i, получим:

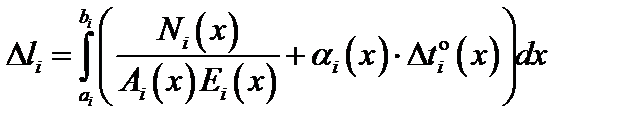, (3.3)

где a_i, b_i­ – координаты начала и конца участка i в выбранной системе координат. Суммируя абсолютные деформации участков, получим полную абсолютную деформацию (удлинение или укорочение) всего стержня при действии силовых и температурных нагрузок:

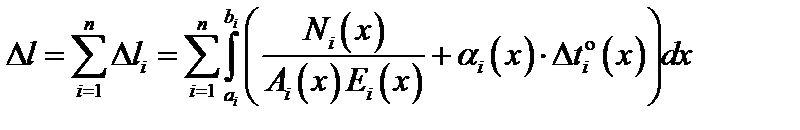. (3.4)

Введем в рассмотрение функцию u_i(x) продольных перемещений сечений на участке i. Нетрудно заметить, что продольное перемещение сечения складывается из перемещения стержня как жесткого диска (перемещения начального сечения) и абсолютной деформации части стержня, заключенной между начальным и рассматриваемым сечениями. Для произвольного сечения на участке i

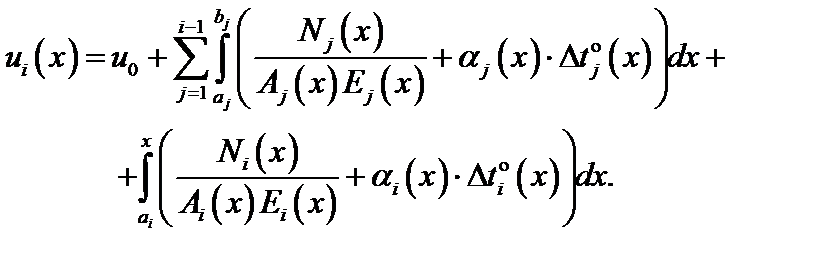(3.5)

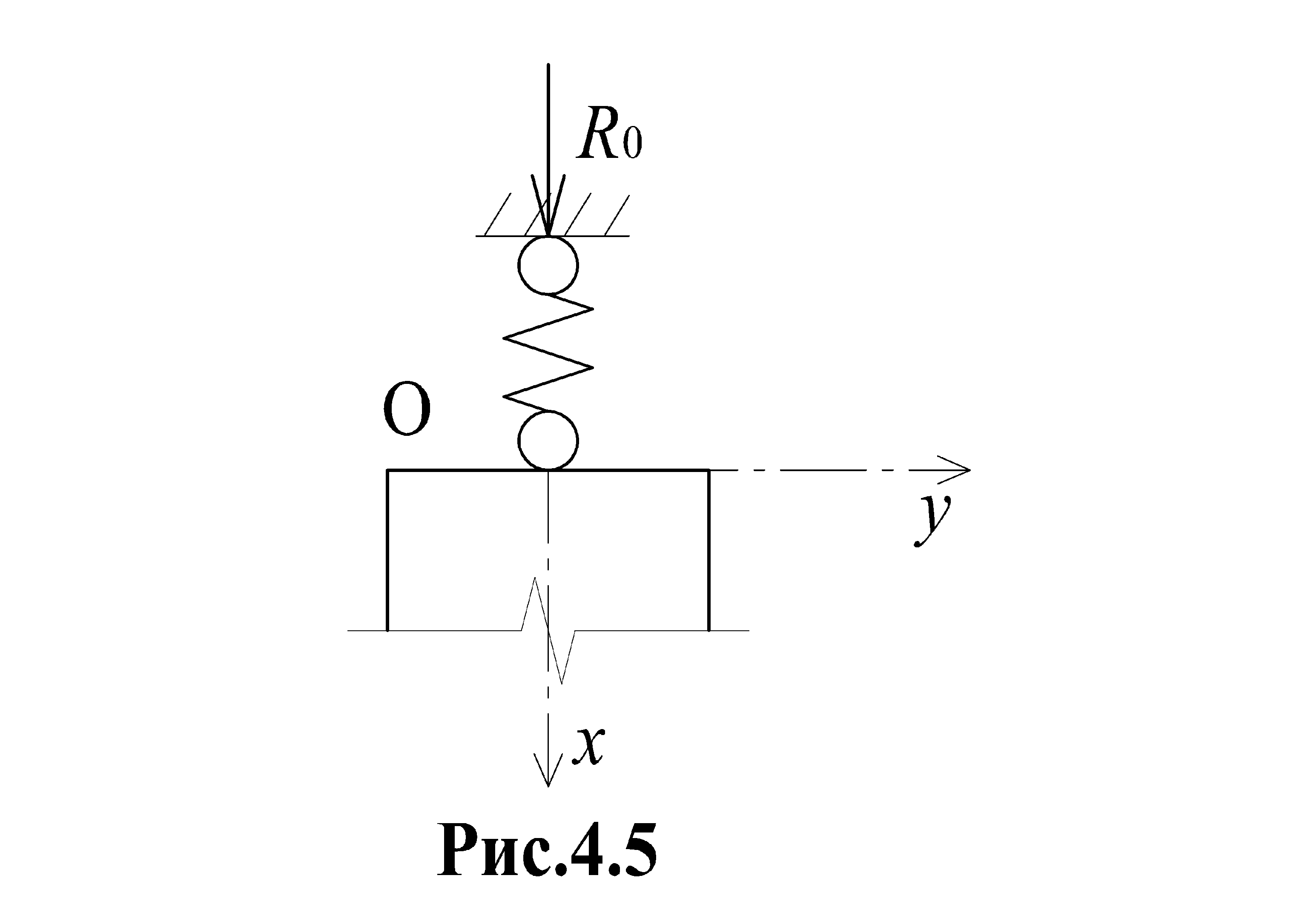
При жестком (неподатливом) закреплении начального сечения (рис. 3.3) u₀ = 0. В случае, когда начальное сечение закреплено линейно-податливой связью (опорой),

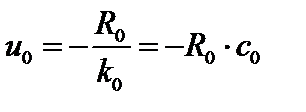, (3.6)

где R₀ – опорная реакция; k₀ (кН/м) – жесткость опоры; 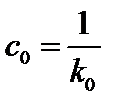(м/кН) – податливость опоры.

В случае, если 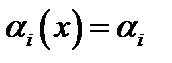, , 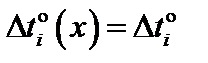i = 1, …, n (равномерное температурное воздействие на участках),

+

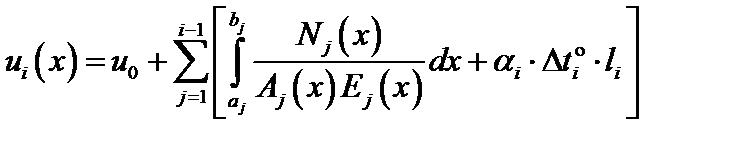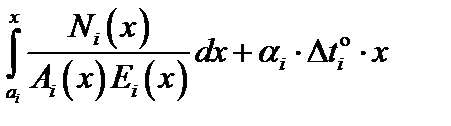+ . (3.7)

При 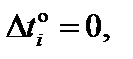i = 1, …, n (температурное воздействие отсутствует) в выражениях (3.2)–(3.7) отсутствуют члены, зависящие от изменения температуры материалов на участках.