37. Проверим, равна ли нулю сумма комплексных токов?
İ = İа + İ b + İ c; İ = 0, т.е. расчет токов верен.
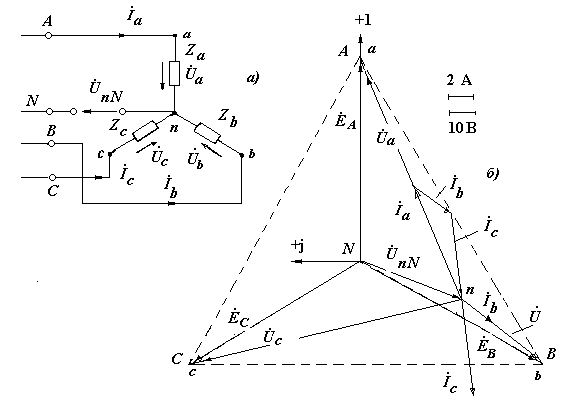
Рис. 2.11. Схема и векторные диаграммы токов и напряжений к задаче № 2.10 (соединение звездой без нейтрального провода)
38. C учетом полученных данных строится векторная диаграмма токов и напряжений (рис. 2.11, б).
39. Комплекс мощности фазы а:
S a = Ů a Ia*; S a = 1415e j0 = 1415 + j0 ВА;
активная, реактивная мощности фазы а: Ра = 1415 Вт; Qa = 0 вар.
40. Комплекс мощности фазы b:
S b = Ů b Ib*; S b = 157,7e j0 = 157,7 + j0 ВА;
активная, реактивная мощности фазы b: Р b = 157,7 Вт; Qb = 0 вар.
41. Комплекс мощности фазы c:
S c = Ů c Ic*; S c = 1089e-j90 = 0 - j1089 ВА;
активная, реактивная мощности фазы c: Рс = 0 Вт; Q с = - 1089 вар.
42. Полная мощность на нагрузке трех фаз:
S = Sa + Sb + Sc; S = 1913е−j34,7 = 1573 - j1089 ВА;
активная, реактивная мощности на нагрузке трех фаз:
Р = 1573 Вт; Q = -1089вар.
43. Режим 3. Обрыв провода фазы А при наличии нейтрального провода (рис. 2.12, а).
В случае наличия нейтрального провода векторы всех фазных токов и напряжений, как и в случае 1, имеют общее начало в т. N = n (рис. 2.12, б), поэтому Ů nN = 0. При этом: фазные напряжения Ů a, Ů b, Ů c, рассчитанные в пп. 5-8 не изменяются; ток в фазе а – отсутствует. Следовательно: İа = 0; токи İ b, İс в фазах b и с – не изменяются.
44. Комплексный суммарный ток в нейтральном проводе:
İ N = İ a + İ b + İ c; İ N = - 6,8 − j7,6 = 10,24e-j131,9 A.
45. C учетом полученных данных строится векторная диаграмма токов и напряжений (рис. 2.12, б).
46. Комплекс мощности фазы а:
S a = Ů a Ia*; S a = 0e j0 = 0 + j0 ВА;
активная, реактивная мощности фазы а:Ра = 0 Вт; Qa = 0 вар.
47. Комплекс мощности фазы b:
S b = Ů b Ib*; S b = 807e j0 = 807 + j0 ВА;
активная, реактивная мощности фазы b; Р b = 807 Вт; Qb = 0 вар.
48. Комплекс мощности фазы c:
Sc = Ů c Ic*; S c = 537e-j90 = 0 - j537 ВА;
активная, реактивная мощности фазы c: Рс = 0 Вт; Q с = -537 вар.
49. Полная мощность на нагрузке трех фаз:
S = Sa + Sb + Sc; S = 806 − j537 = 970e-j33,7 ВА;
активная, реактивная мощности на нагрузке трех фаз
Р1 = 806 Вт; Q1 = - 537 вар.
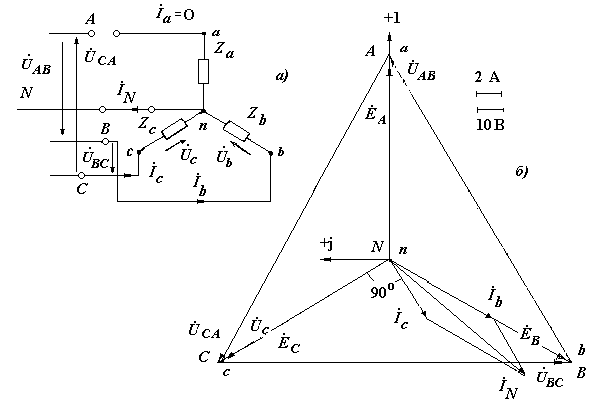
Рис. 2.12. Схема и векторные диаграммы токов и напряжений к задаче № 2.10
(соединение звездой с обрывом фазы А с нейтральным проводом)
50. Режим 4. Короткое замыкание фазы В и обрыв нейтрального провода (рис. 2.13, а).
В данном режиме потенциалы точек n и b совпадают, поэтому на векторной диаграмме (рис. 2.13, б) нейтральная точка n ²сместится² в точку b и Ů nN = Ů b. При отсутствии нейтрального провода нагрузка фаз А и С оказывается включенными на линейное напряжение, т.е. Ůа = Ů ab, Ů b = 0; Ů c = - Ů bc. Сумма токов в точке n равна 0; значения Ů ab, Ů bc рассчитаны в пп. 9, 10.
51. Комплексный ток İ a в фазе А:
İa = Ů а/Za = Ůab/Za; İa = 11e j30 = 9,53 + j5,5 A.
52. Комплексный ток İc в фазе C; İc = Ůc/Zc = -Ůbc/Zc:
İc = 220е j90/30e−j90= 7,33e 180 = −7,33 + j0 A.
53. Комплексный ток в İ b в проводе фазы В:
İb = -(İa + İc); İb = 5,9e-j111 = -2,20 - j5,2 A.








