23. Расчет и измерение активной мощности по методу двух ваттметров.
24. Расчет активной мощности с учетом cos j .
25. Расчетное значение Р1р активной мощности, которое должен показывать ваттметр W1: Р1р = UABI Асosj1 = UABI Асos(Ů AB۸İА);
Р1р = 370×17,6сos(82 о - 14,8 о) = 2533 Вт.
26. Расчетное значение Р2р активной мощности, которое должен показывать ваттметр W2: Р2р = U С B I Ссosj2 = UCBICсos(Ů CB۸İ C);
Р2р = 370×17,6сos(142 о − 134 о) = 6482 Вт.
27. Расчетная суммарная мощность Рр, потребляемая источником:
Рр = Р1р + Р2р; Рр = 9016 Вт.
28. Расчет активной мощности с учетом комплексных значений токов и напряжений.
29. Полная комплексная мощность S1:
S1= Ů AB I*А; S1 = 370,1e j82 17,6e −j14,7 = 6533e j67,18 = 2533 + j6022 ВА.
30. Показание ваттметра W1 – активная мощность Р1:
Р1= ReS1; Р1 = 2533 Вт.
31. Полная мощность S2: S2 = Ů cb IC* = - Ů bc IC*;
S2 = 370,5e j14117,6e −j135= 6533е j7,17 = 6482 + j817 ВА.
32. Показание ваттметра W2 – активная мощность Р2:
Р2 = ReS2; Р2 = 6482 Вт.
33. Активная мощность Р, потребляемая источником:
Р = Р1 + Р2; Р = 9016 Вт.
34. Построение векторной топографической диаграммы.
Векторная топографическая диаграмма для всех фаз строится следующим образом (рис. 2.9, б). Выбираем оси +1 и +j. Учтем, что Ůbс = 200e j0 = 200 + j0 B, т.е. вектор фазного напряжения приемника Ů b с (в выбранном масштабе) направлен по оси +1. К его концу достраивается вектор Ůа b (с учетом величины и углов) и т.д. Треугольники векторов токов строятся в вершинах соответствующих точек a, b, c .
Задача № 2. 10
Параметры схемы четырехпроводной цепи переменного тока, представленной на рис. 2.10, а, приведены таблице 2.10. Приемники соединены звездой с нейтральным проводом (генератор не указан). Заданы: линейное напряжение Uл, активные ri, реактивные xiL или xiC (индекс ²L² – индуктивное, индекс ²С² - емкостное) сопротивления фаз a, b, c приемника.
Необходимо рассчитать параметры приведенной сети для различных режимов:
- режим 1: четырехпроводная сеть (с нейтральным проводом);
- режим 2: обрыв нейтрального провода;
- режим 3: обрыв провода фазы А при наличии нейтрального провода;
- режим 4: короткое замыкание фазы В и обрыв нейтрального провода.
Таблица 2.10
Задание к задаче № 2.10
| Параме тры | Последняя цифра номера зачетки | Пример | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Uл, В | 380 | 220 | 127 | 380 | 220 | 127 | 380 | 220 | 127 | 380 | 220 |
| ra, Ом | 0 | 10 | 20 | 25 | 30 | 35 | 40 | 35 | 30 | 25 | 20 |
| rb, Ом | 25 | 30 | 35 | 40 | 35 | 30 | 25 | 20 | 10 | 0 | 20 |
| rc, Ом | 0 | 0 | 0 | 7 | 24 | 24 | 7 | 18 | 24 | 10 | 0 |
| Предпоследняя цифра номера зачетки | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| xaL, Ом | 30 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 10 | 5 | 0 |
| xbL, Ом | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| xcC, Ом | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
Для всех перечисленных режимов необходимо нарисовать схему, в соответствии с исследуемым режимом, а также рассчитать:
- комплексы фазных токов и напряжений;
- комплексные сопротивления;
- мощность трехфазной системы;
- построить векторные диаграммы фазных токов и напряжений;
Для электрической схемы, соответствующей номеру варианта, выполнить следующие этапы расчета.
1. Зарисовать схему и записать задание, соответствующее номеру варианта (рис. 2.10, а, табл. 2.10).
2. В соответствии со схемой предполагается наличие несимметричной нагрузки. Поэтому весь расчет производить для каждой из фаз, например а. Условно принимаем, что вектор Ůа направлен по оси действительных величин (рис. 2.10, б), т.е. полагается, что начальная фаза фазного напряжения Ůа равна нулю.
3. Определить (рассчитать) параметры цепи.
4. Режим 1. Четырехпроводная сеть (с нейтральным проводом) (рис. 2.10, а)
5. Задаемся нулевой фазой для фазного напряжения Ůа; jua = 0 град.
6. Комплекс действующего фазного напряжения Ůа (пренебрегаем падением напряжения на линии):
Ů a = Ė A = U ae jju а; Ů a = Ė A = 127e j0 = 127+ j0 B.
7. Комплекс действующего фазного напряжения Ů b (пренебрегаем падением напряжения на линии):
Ů b = Ė B = U be-j120; Ů b = Ė B = 127e-j120 = -63,5 - j110 B.
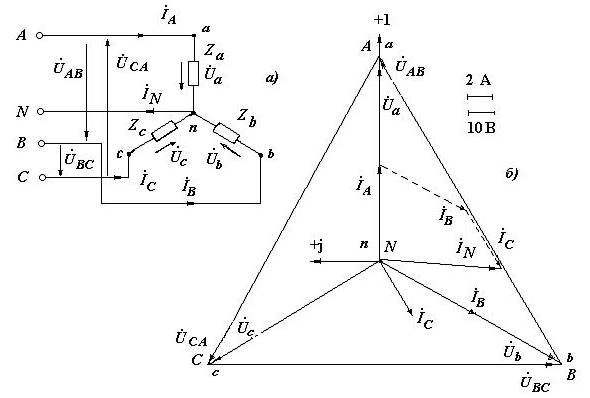
Рис. 2.10. Схема и векторные диаграммы токов и напряжений к задаче
№ 2.10 (соединение звездой с нейтральным проводом)
8. Комплекс действующего фазного напряжения Ů c (пренебрегаем падением напряжения на линии):
Ů c = Ė C = U ce+j120; Ů c = Ė C = 127e+j120 = −63,5 + j110 B.
9. Комплекс действующего линейного напряжения Ůа b на приемнике:
Ů ab = Ů ab = Ů a - Ů b; Ů ab = 220e+j30 = 191 + j110 B.
10. Комплекс действующего линейного напряжения Ů bc на приемнике: Ů bc = Ů bc = Ů b - Ů c; Ů bc = 220e-j90 = 0 - j220 B.
11. Комплекс действующего линейного напряжения Ů ca на приемнике: Ů ca = Ů ca = Ů c - Ů a; Ů ca = 220e j150 = 190 + j110 B.
12. Комплексное сопротивление нагрузки Z a фазы А:
Z a = 20 + j0 = 20e+j0 Ом.
13. Комплексное сопротивление нагрузки Z b фазы В:
Z b = 20 + j0 = 20e+j0 Ом.
14. Комплексное сопротивление нагрузки Z c фазы С:
Z c = 0 - j30 = 30e-j90 Ом.
15. Комплексный ток İ a = İ a: İ a = Ů a/Z a; İ a = 6,35 + j0 = 6,35e j0 A.
16. Комплексный ток İ b = İ b: İ b = Ů b/Z b; İ b = -3,18 − j5,5 = 6,35e-j120 A.
17. Комплексный ток İ c= İС: İ c = Ů c /Z c; İ c = -3,67 − j2,1 = 4,23e j210 A.
18. Комплексный ток в нейтральном проводе:
İ N = İ a + İ b + İc ; İ N = -0,49 − j7,62 = 7,63e-j94 A.








