34. Рассчитываем токи в ветвях с учетом направлений токов и действующих ЭДС.
35. Определяем İ1: İ1 = (Ė1− Ů a с)/Z1; İ1= 3,282 + j0,1025 = 3,28е j1,79A.
36. Определяем İ2: İ2 = (Ů a с - Е2) / Z2; İ2 = 3,179 - j3,179 = 4,496е -j45 A.
37. Определяем İ3: İ3 = (Ė3 − Ů a с)/ Z3;
İ3= -0,1025 - j3,28 = 3,283е-j91,8A.
38. Определение токов в ветвях методом эквивалентного генератора. Метод предполагает, что в ветви, содержащей искомый ток, имеется разрыв, так что между точками а и с приложено напряжение холостого хода Ůхх.
39. Исследуем схему (рис. 2.7, а), размыкая ветвь aec (разрыв между точками а и с), получаем схемы (б, в).
40. Согласно этапам метода с учетом выбранных положительных направлений токов, напряжения Ůхх и ЭДС, необходимо определить:
- определить ЭДС эквивалентного генератора, равное напряжению холостого хода Ėген= Ůхх;
- внутреннее сопротивление эквивалентного генератора Zген как входное сопротивление цепи с разрывом;
- ток в искомой ветви, равный: İ2 = (Ėген - Ė2)/(Z ас + Z2). (17)
41. Рассчитываем Ėген = Ůхх, используя метод двух узлов аналогично (16): Ůхх =(Ė3Y3 + Ė1Y1)/(Y1+ Y3); Ėген=Ůхх = 313,15е-j45 = 221,42 - j221,42 В.
42. При этом режиме входная проводимость Yэкв цепи:
Yэкв = Y1 + Y3; Yэкв = 0,0224е j0 = 0,0224 + j0 См.
43. Внутреннее сопротивление генератора Zген:
Zген = 1/Yэкв; Zген = 44,64е j0 = 44,64 + j0 Ом.
44. Для схемы с эквивалентным генератором, приведенной на рис. 3.7, в, рассчитываем по (17) İг = İ2 (с учетом, что в варианте Ė2 = 0):
İг = İ2 = (Ėген - Ė2)/(Zген + Z2); İг = İ2 = 4,496e- j45 == 3,179 - j3,179 А.
45. Сравнивая результаты расчета, делаем вывод, что значения токов, полученные различными методами, идентичны друг другу.
46. Для построения векторной диаграммы необходимо учесть значения и направления векторов комплексных токов и напряжений (рис. 2.7, г).
47. Составление баланса мощностей.
48. Комплексная полная мощность S1 источника Ė1:
S1 = Ė1I1*; S1 = 100e j03,28е −j1,79 = 328,37e -j1,79 = 328,21 - j10,26 ВА.
49. Комплексная полная мощность S2 источника Ė2:
S2 = Ė2I2*; S2 = 0 ВА.
50. Комплексная полная мощность S3 источника Ė3:
S3 = Ė3I3*; S3 = 328,37e j1,79 = 328,21 + j10,26 ВА.
51. Активная составляющая мощности источников:
Рист = åReSi; Рист = 656,41 Вт.
52. Реактивная составляющая мощности источников
Qист = åImSi; Qист = 0 вар.
53. Активная мощность потребителей
Pпот = åIi2ReZi; Pпот = 3,282×7 +4,52×25+3,282×7 = 656,41 Вт.
54. Реактивная мощность потребителей:
Qпот= åIi2ImZi; Qпот= 3,282·24 + 0 – 3,282·24 = 258,8 + 0 - 258,8 = 0 вар.
55. Сравнивая результаты расчета, делаем выводы:
- суммы активных мощностей источников и потребителей равны;
- суммы реактивных мощностей источников и потребителей равны
56. Запись оригиналов ЭДС, токов и напряжений.
57. Оригинал e1(t): e1(t) = Em1sin(wt + j1); e1(t) = 141,4 sin(314t) В.
58. Оригинал e2(t): e2(t) = Em2sin(wt + j2); e2(t) = 0 В.
59. Оригинал e3(t): e3(t) = Em3sin(wt + j3); e3(t) = 141,4sin(314t - 90o) В.
60. Оригинал i1(t): i1(t) = Im1sin(wt + ji1); i1(t) = 4,64sin(314t + 1,79 o) A.
61. Оригинал i2(t): i2(t) = Im2sin(wt + ji2); i2(t) = 6,36sin(314t - 45 o) A.
62. Оригинал i3(t): i3(t) = Im3sin(wt + ji3); i3(t) = 4,64sin(314t -91,79 o) A.
63. Оригинал uxx(t):
uxx(t) = Umxxsin(wt + ji2); Uxx(t) = 442,8sin(314t - 45o) В.
Примечание: решение уравнений (1)-(3) может быть найдено с помощью анализа и использования матриц коэффициентов.
Задача № 2.8
Схема трехпроводной цепи переменного тока (фазы А, В, С) представлена на рис. 2.8. К генератору (на схеме не показан) подключены приемники фаз a, b, c, соединенные ²звездой². Активная мощность каждого приемника равна Р, напряжение приемника Uпр, коэффициент мощности приемника сosj2. Каждый провод линии, соединяющий генератор и приемник, имеет активное сопротивление rл и индуктивное сопротивление xL, представленные в таблице 2.8.
Таблица 2.8
Задание к задаче № 2.8
| Параметры | Последняя цифра номера зачетки | Пример | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Рпр, кВт | 1,9 | 2,0 | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 | 2,7 | 2,8 | 2,9 |
| Uпр, В | 380 | 660 | 220 | 380 | 660 | 220 | 380 | 660 | 220 | 380 | 220 |
| Предпоследняя цифра номера зачетки | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| cos j 2 | 0,70 | 0,69 | 0,68 | 0,67 | 0,66 | 0,65 | 0,64 | 0,63 | 0,62 | 0,61 | 0,60 |
| rл, Ом | 0,80 | 0,78 | 0,76 | 0,74 | 0,72 | 0,70 | 0,68 | 0,66 | 0,64 | 0,62 | 0,60 |
| xл, Ом | 6 | 5,5 | 5,0 | 4,5 | 4,0 | 3,5 | 3,0 | 2,5 | 2,0 | 1,5 | 1,0 |
С учетом параметров схемы необходимо:
- найти напряжение на зажимах генератора;
- активную и реактивную мощности генератора;
- рассчитать падение и потерю напряжения в линии;
- найти параметры схемы для построения векторной диаграммы.
Примечание: если в тексте не говорится, о каком напряжении U идет речь, то однозначно понимается, что имеется в виду линейное напряжение, т.е. U = Uл.
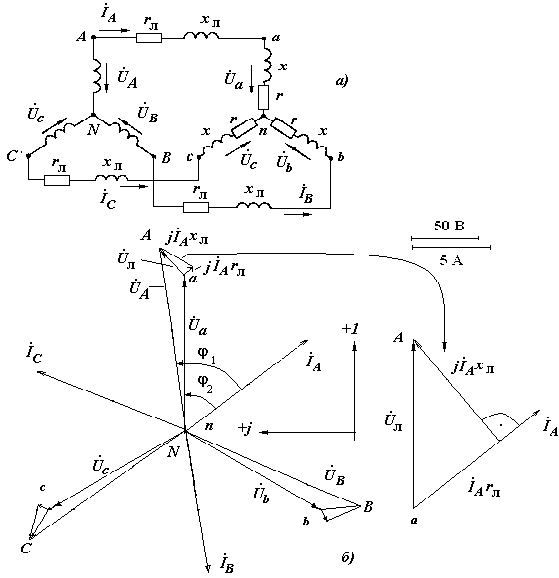
Рис. 2.8. Схема (а) и векторные диаграммы токов и напряжений (б) к задаче № 2.8
Для электрической схемы, соответствующей номеру варианта, выполнить следующие этапы расчета.
1. Зарисовать схему и записать задание, соответствующее номеру варианта (рис. 2.8, табл. 2.15).
2. В соответствии со схемой предполагается: генератор соединен звездой; при симметричной нагрузке напряжение между нейтралями генератора и приемника равны нулю, поэтому каждую фазу схемы можно рассматривать независимо от других фаз и весь расчет производить только для одной фазы, например, а.
3. Определить (рассчитать) параметры.
4. Линейное напряжение Uпр.л приемника:
Uпр. л = Uab = Ubc = Uca; Uпр. л = 220 В.
5. Фазное напряжение Uпр. ф : Uпр. ф = Uп/Ö3; Uпр. ф = 127 В.
6. Комплексное фазное напряжение приемника Ůа, принимая, что его начальная фаза равна нулю: Ůа = 127 + j0 В.
7. Фазный ток I приемника, равный фазному и линейному току:
Pпр=Ö3UпIфcosj2 = =Ö3UпIлcosj2; Iф = I а = Ib = Ic = IA = IB = IC = 12,68 A.
8. Угол j2, на который ток фазы отстает от напряжения: j2 = 53,13 о.
9. Модуль комплексного сопротивления Zп фаз приемника:
Zп = Uф /Iф; Zп = 10 Ом.
10. Активное сопротивление r фаз приемника:
r = Zп cosj2; r = 6,01 Ом.
11. Реактивное (индуктивное) х L сопротивление фаз приемника:
х L = Zп sinj2; х L = 8 Ом.
12. Модуль комплексного сопротивления Zл линии передачи:
Zл = (rл2 + хл2)0,5; Zл = 1,17 Ом.
13. Комплексное сопротивление Zл линии передачи:
Zл = 0,6 + j1= 1,17е j59 Ом.
14. Модуль полного комплексного сопротивления Z фаз приемника с учетом сопротивления линии: Z = [(r + rл)2 + (х L + хл)2]0,5; Z = 11,17 Ом.
15. Фазное напряжение генератора UA, обеспечивающее ток Iф на сопротивлении Z: UA = ZI; UA = 141,7 В.
16. Линейное напряжение генератора UA В, обеспечивающее ток Iф на сопротивлении Z: U АВ = Ö3UAф; U АВ = 245,5 В.
17. Потеря напряжения DUл на проводе линии:
DUл = U АВ - U пр. л; DUл = 25,5 В.
18. Падение напряжения на активном сопротивлении провода линии:
Urл = rлIф; Urл = 7,6 В.
19. Падение напряжения на индуктивном сопротивлении провода линии: U хл = хлIф; U хл = 12,7 В.
20. Коэффициент мощности генератора:
cosj1= (rл + r)/Z; cosj1= 0,59; j1 = 53,75 о.
21. Активная мощность генератора c учетом Uфг = U А= U В= U С:
P = 3UфгIфcosj2 = 3(rл + r)Iф2; P = 3,19 кВт.
22. Полная мощность генератора:
S = Ö3UлгIф = 3UфгIф; S = 5,4 кВА.
23. Реактивная мощность генератора: Q = (S2 − Р2)0,5; Q = 4,35 квар.
24. Построение векторной топографической диаграммы.
Векторная топографическая диаграмма для всех фаз строится следующим образом (рис. 2.8, б). Выберем направление осей +1 и +j. Учтем, что Ůа = 127 + j0 В, т.е. вектор Ůа направлен по оси +1. Вектор фазного напряжения приемника Ůа и вектор фазного тока İА сдвинуты один относительно другого на угол 53 о. Прибавляя к вектору Ůа вектор Ů rл и вектор Ůхл, получим вектор фазного напряжения генератора ŮА. На рис. 2.8, в, представлен вектор Ůпр, равный сумме векторов Ů rл и Ůхл и представляющий собой вектор падения напряжения в проводе линии А.
Задача № 2.9
Схема симметричной трехпроводной цепи переменного тока представлена на рис. 2.9, а. Генератор с фазами А, В, С − не указан. Приемники (фазы ab, bc, ca) соединены треугольником.
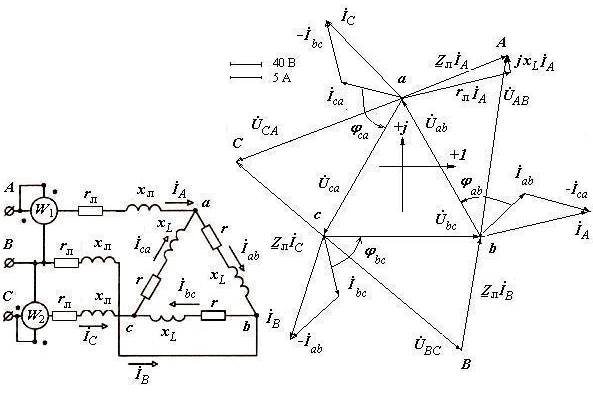
а) б)
Рис. 2.9. Схема (а) и векторные диаграммы токов и напряжений (б) к задаче № 2.9
Заданы: напряжение Uпр на зажимах приемника, активное r и реактивное х L сопротивления приемника, сопротивления линии rл и хл. Параметры цепи представлены в таблице 2.9. С учетом параметров цепи необходимо определить:
- линейные напряжения генератора:
- токи в линиях;
- показания ваттметров Р1, Р2 и мощность Р, потребляемую источником;
- параметры схемы для построения векторной диаграммы.
Таблица 2.9
Задание к задаче № 2.9
| Парамет ры | Последняя цифра номера зачетки | Пример | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Uпр, В | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| r, В | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 |
|
| Предпоследняя цифра номера зачетки | ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| х L, Ом | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 19 |
| rл, Ом | 9 | 10 | 11 | 12 | 6 | 5 | 4 | 3 | 2 | 1 | 8 |
| xл, Ом | 10 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 1 | 1 |
Для электрической схемы, соответствующей номеру варианта, выполнить следующие этапы расчета.
1. Зарисовать схему и записать задание, соответствующее номеру варианта (рис. 2.9; табл. 2.9).
2. В соответствии со схемой предполагается: при симметричной нагрузке каждую фазу схемы можно рассматривать независимо от других фаз и весь расчет производить только для одной фазы, например, ab, bc, ca. Условно принимаем, что вектор Ůb c направлен по оси действительных величин (рис. 2.9, б). Т.е. полагается, что начальная фаза фазного напряжения Ů b с равна нулю.
3. Определить (рассчитать) параметры схемы.
4. Комплекс действующего фазного напряжения:
Ů b с = Ue j0; Ůbс = 200e j0 = 200 + j0 B.
5. Комплекс действующего фазного напряжения Ů ab:
Ů ab = 200e+j120 = -100 + j173 B.
6. Комплекс действующего фазного напряжения Ů ca:
Ů ca = 200e-j120 = - 100 - j173 B.
7. Комплексное сопротивление Zab фазы приемника:
Z ab = Z bc = Z ca = r + jxL; Z ab = 5 + j19 = 19,65е j75,3 Ом.
8. Комплексный фазный ток İ ab:
İ ab = Ů ab/Z ab; İ ab = 10,18e j44,7 = 7,23 + j7,17 A.
9. Комплексный фазный ток İ bc:
İ bc = Ů bc/Z bc; İ bc = 10,18e-j75,3 = 2,6 - j9,84 A.
10. Комплексный фазный ток İ ca:
İ ca = Ů ca/Z ca; İ bc = 10,18e-j195,3 = -9,8 + j2,7 A.
11. Линейный ток İА по первому закону Кирхгофа:
İ А = İab - İca ; İ А = 17,1 + j4,5 = 17,6e j14,7 A.
12. Линейный ток İ B по первому закону Кирхгофа:
İB = İbc - İab; İB = -4,6 - j17 = 17,6e-j105 A.
13. Линейный ток İ C по первому закону Кирхгофа:
İC = İca - İbc; İC = -12,4 + j12,5 = 17,6e j135 A.
14. Падение напряжения на активном сопротивлении линии A:
Ů r = rлİА; Ů r = 141e j14,7 = 136 + j35 В.
15. Падение напряжения на реактивном сопротивлении линии A:
Ůх = j хлİА; Ů r = 17,6e j105 = -4,47 + j17,1 В.
16. Комплексное сопротивление Zл линии фазы:
Zл = rл + jxл; Zл = 8 + j1= 8,06e j7,13 Ом.
17. Падение напряжения на комплексном сопротивлении линии фазы А:
ŮлА = ZлİА; ŮлА = 142,15e j21,9 = 132 + j53 В.
18. Падение напряжения на комплексном сопротивлении линии фазы В:
ŮлВ = ZлİВ; ŮлВ = 142,15e-j98,1 = -20,1 - j140,7 В.
19. Падение напряжения на комплексном сопротивлении линии фазы С:
ŮлС = ZлİС; ŮлА = 142,15e j141,9 = -111,8 + j87,7 В.
20. Линейное напряжение (на клеммах) генератора Ů AB c учетом падения напряжения на проводах линии А и В (рис. 2.9, а):
Ů AB = Ůab + Ůла - ŮлВ; Ů AB = 52 + j367 = 370,55e j81,93 B.
21. Линейное напряжение (на клеммах) генератора Ů BC c учетом падения напряжения на проводах линии B и C:
Ů BC = Ůb c + ŮлВ - ŮлС; Ů BC = 292 - j228 = 370,55e-j38,07 B.
22. Линейное напряжение (на клеммах) генератора Ů C А c учетом падения напряжения на проводах линии С и А:
Ů C А = Ů c а + ŮлС - ŮлА; Ů CA = -344 - j139 = 370,5e-j158,07 B.








