1. Зарисовать схему и записать задание, соответствующее номеру варианта (рис. 2.5, табл. 2.5).
2. Определить (рассчитать) параметры схемы.
3. Полная мощность S1 цепи до улучшения коэффициента мощности:
S1 = UI; S1 = 69960 ВА.
4. Начальный коэффициент мощности cosj1:
P1= S1cosj1; cosj1 = 0,60.
5. Значение j1: j1 = 53,13 град.
6. Реактивная мощность цепи до улучшения коэффициента мощности
Q1 = S1sinj1; Q1 = 559549,99 ВАр.
7. Суммарная активную мощность, обеспечивающую возможность подключения новой нагрузки: P2 = P1+ Pдоп; P2 = 62000 Вт.
8. Улучшенное значение коэффициента мощности cosj2 при неизменной полной мощности сети: P2 = S1cosj2; cosj2 = 0,886.
9. Значение j2: j2 = 27,61 град.
10. Добавочный ток осветительной нагрузки: Iдоб=Pдоп/U; Iдоб =90,91 A.
11. Величина реактивной мощности Q2, потребляемой из сети после изменения: Q2 = S1sinj2; Q2 = 32419,9 вар.
12. Изменение реактивной мощности DQ:
DQ = Q1 - Q2; DQ = 23540,09 вар.
13. Необходимая дополнительная реактивная мощность Q С, обеспечиваемая батареей конденсаторов: Q С = DQ; Q С = 23540 вар.
14. Значение емкости С батареи конденсаторов:
C = Q С /U2w; C = 1548,93 мкФ.
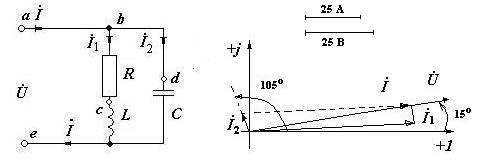
15. Рисуем и письменно объясняем векторную диаграмму (рис. 2.8, в).
Задача № 2.6
Цепь, представленная на рис. 2.6, а, находится в режиме резонанса тока. На входе цепи действует переменное напряжение u(t), оригинал которого равен u(t) = Umsin(wt + yU). При этом мгновенный ток i(t) в цепи изменяется по закону: i(t) = i msin(wt + yI). Параметры цепи приведены в таблице 2.6.
а) б)
Рис. 2.6. Схема (а) и векторная диаграмма токов и напряжения (б) к задаче № 2.6
С учетом параметров цепи требуется определить:
- значение емкости конденсатора С;
- выражения для оригиналов токов i1(t), i2(t), напряжения u(t);
- мощности, потребляемые цепью в режиме резонанса;
- параметры схемы для построения векторной диаграммы токов цепи при резонансе.
Таблица 2.6
Задание к задаче № 2.6
| Параметры | Последняя цифра номера зачетки | Пример | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| i m, A | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 |
| y I , град | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 |
| R, Ом | 11 | 10 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Предпоследняя цифра номера зачетки | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| XL, Ом | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 |
| w0, рад /с | 104 | ||||||||||
Для электрической схемы, соответствующей номеру варианта, выполнить следующие этапы расчета.
1. Зарисовать схему и записать задание, соответствующее номеру варианта (рис. 2.6, а; табл. 2.5).
2. Определить (рассчитать) параметры схемы.
3. Оригинал тока i(t), в соответствии с заданием варианта:
i(t) = 11sin(104t + 15о) А.
4. Выражение для комплекса действующего значения тока İ (комплексного тока), соответствующего оригиналу в алгебраической и показательной формах: İ = (11/Ö2)e j15 = 7,778 e j15 = 7,51 + j2,01 A.
5. Поскольку в цепи выполняется режим резонанса токов, учесть, что условие резонанса токов характеризуется равенством модулей реактивных проводимостей параллельных ветвей ImYbce = ImYbde. Для этого рассчитываются следующие величины:
6. Комплексное сопротивление Z1 ветви bce :
Z1= R + jwL; Z1= 9 + j2 = 9,22e j12,54 Ом.
7. Комплексная проводимость Y1 ветви bce :
Y1 = 1/ Z1; Y1 = 0,108e- j12,54 = 0,106- j0,0235 Cм.
8. Модуль реактивной Y2 комплексной проводимости ветви bde:
ImY2 = ImY3; ImY2 = 0,0235 См.
9. Величина емкости С: ImY2 = 1/XC = w0C; C = 2,353 мкФ.
10. Комплексное сопротивление Z2 ветви bde:
Z2= 0 - jXC = - j/w0C; Z2 = 42,5e -j90 = 0 - j42,5 Ом.
11. Комплексная проводимость Y2 ветви bde :
Y2 = 1/Z2; Y2= 0,0235е j90 = 0 + j0,0235 Ом.
12. Полная комплексная проводимость Y цепи ae :
Y = Y1 + Y2; Y = 0,106е j0 = 0,106 + j0 Cм.
13. Комплексное напряжение Ů (комплекс действующего напряжения): Ů = İ/Y; = 73,46е j15 = 70,96 + j19,004 B.
14. Комплекс напряжения Ů m (комплексная амплитуда):
Ů m = ŮÖ2; Ů = 103,89е j15 = 100,4 + j26,875 B.
15. Оригинал u(t): u(t) = 103,89sin(104t + 15о) B.
16. Комплексный ток İ1: İ1 = Ů/Z1; İ1 = 7,97е j2,46 = 7,96 + j0,3425 А.
17. Комплекс İ1m: İ1m = İ1Ö2; İ1m = 11,27е j2,46A.
18. Оригинал i1(t): i1(t) = 11,27sin(104t + 2,46о) A.
19. Комплексный ток İ2: İ2 = Ů/Z2; İ2 = 1,723е j105,1 = -0,449 + j1,669 А.
20. Комплекс İ2m: İ2m= İ2Ö2; İ2m = 2,4е j105 A.
21. Оригинал i2(t): i2(t) = 2,44sin(104t + 105,1о) A.
22. Активная мощность при резонансе c учетом j = 0:
P = UIcosj; P = 7,8×73,5 = 571,39 Вт.
23. Реактивная мощность при резонансе c учетом j = 0:
Q = UIsinj; Q = 0 вар.
24. Полная мощность при резонансе: S = (P2 + Q2)0,5; S = 571,39 ВА.
25. Рисуем векторные диаграммы токов и напряжений для цепи при резонансе (рис. 2.6, б).
Задача № 2.7
Параметры схемы, показанной на рис. 2.7, а, приведены в таблице 2.7. Значения ЭДС и сопротивлений электрической цепи заданы в комплексной форме. Принять, что значение Zi = ni +jti, а угловая частота синусоидальных источников ЭДС равна w = 2pf = 314 рад/с.
С учетом параметров схемы определить:
- действующие и комплексные значения токов всех ветвей электрической схемы, пользуясь методами: применения законов Кирхгофа, узлового напряжения (двух узлов);
- составить баланс активной и реактивной мощности источников и приемников энергии;
- записать выражения оригиналов (для мгновенных значений) ЭДС, неизвестных токов и напряжения U ас;
- ток İ2, используя метод эквивалентного генератора;
- построить векторную диаграмму токов и напряжений искомой электрической цепи (в одном масштабе на одном рисунке).
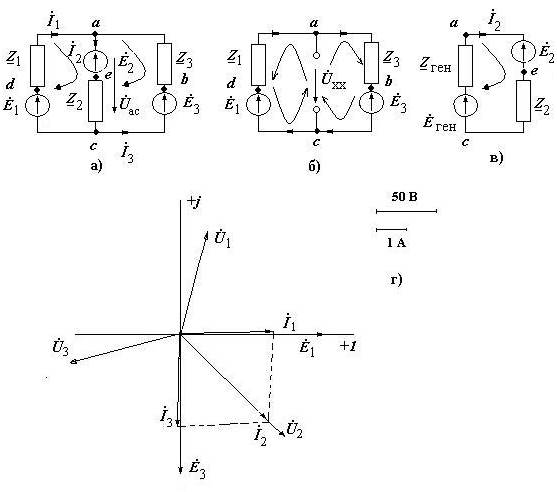
Рис. 2.7. Схемы (а, б, в) и векторные диаграммы токов и напряжений (г) к задаче № 2.7
Этапы решения задачи № 2.7
Для электрической схемы, соответствующей номеру варианта, выполнить следующие этапы расчета.
1. Зарисовать схему и записать задание, соответствующее номеру варианта (рис. 2.7, а; табл. 2.7).
2. Определить (рассчитать) параметры цепи.
3. Комплексное значение ЭДС Ė1 представляется в виде:
Ė1 = 100 + j0 = 100e j0 В.
4. Комплексное значение ЭДС Ė2 представляется в виде:
Ė2 = 0 + j0 = 0 В.
5. Комплексное значение ЭДС Ė3 представляется в виде:
Ė3 = 0 - j100 = 100e-j90 В.
6. Комплексное сопротивление Z1 представляется в виде:
Z1 = 7 + j24 = 25e j73,74 Ом.
Таблица 2.7
Задание к задаче 2.7
| Параме- тры | Последняя цифра номера зачетки | Пример | ||||||||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||||||||
| Ė1, В | 80j | -90 | 100 | -110j | 120 | 110 | -90j | 80 | 60 | -50j | 100 | |||||||||||
| Ė2, В | -40 | 50j | 60 | 70 | -80j | 90 | 80 | -70j | 60 | 50 | 0 | |||||||||||
| Ė3, В | 90 | 80 | -70j | 60 | 50 | -40j | 60 | 70 | -50j | 60 | -100j | |||||||||||
| Предпоследняя цифра номера зачетки | ||||||||||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||||||||
| n | t | n | t | n | t | n | t | n | t | n | t | n | t | n | t | n | t | n | t | n | t | |
| Z 1 , Ом | 17 | -8 | 16 | -7 | 15 | 9 | 14 | 11 | 13 | 13 | 12 | 15 | 11 | 17 | 10 | 19 | 9 | 20 | 8 | 22 | 7 | 24 |
| Z2 Ом | 15 | 10 | 16 | 9 | 17 | 8 | 18 | 7 | 19 | 6 | 20 | 5 | 21 | 4 | 22 | 3 | 23 | 2 | 24 | 1 | 25 | 0 |
| Z3 Ом | 17 | -8 | 16 | -7 | 15 | -9 | 14 | -11 | 13 | -13 | 12 | -15 | 11 | -17 | 10 | -19 | 9 | -20 | 8 | -22 | 7 | -24 |
7. Комплексное сопротивление Z2 представляется в виде:
Z2 = 25 + j0 = 25e j0 Ом.
8. Комплексное сопротивление Z3 представляется в виде:
Z3 = 7-j24 = 25e-j73,74 Ом.
9. Определение токов в ветвях различными методами.
10. Метод с использованием законов Кирхгофа предполагает составление уравнений по I и II законам Кирхгофа.








