3. Определить (рассчитать) значения всех параметров в системе СИ.
4. Оценить, какой резонанс наблюдается в исследуемой цепи? Резонанс напряжений.
5. Значение частоты f0 резонанса напряжений:
XC0 = 1/w0C = Х L0 = w0L; f0 = w0/2p =1/[2p(CL)0,5]; f0 = 134,58 Гц.
6. Значение реактивного индуктивного сопротивления Х L0(f0) при резонансе: Х L0 = w0L; Х L0(f0) = 33,81 Ом.
7. Значение реактивного емкостного сопротивления ХС0(f0) при резонансе: XC0 = 1/w0C; ХС0(f0) = 33,81 Ом.
8. Модуль полного комплексного сопротивления цепи при резонансе:
Z(f0) = [R2 + (Х L0 - XC0)2]0,5; Z(f0) = 10 Ом.
9. Модуль тока İ при резонансе: I(f0) = U/Z(f0); I(f0) = 14 А.
10. Модуль напряжения на индуктивности в режиме резонанса:
UL(f0) = I(f0)XL(f0); UL(f0) = 472,29 В.
11. Модуль напряжения на конденсаторе:
U С(f0) = I(f0)X С(f0); U С(f0) = 472,29 В.
12. Коэффициент усиления напряжения К:
К = UL/U = U С/U ; К = 3,38.
13. Величина добротности: Q = XL/R = XLIрез/RIрез= К; Q = 3,38.
14. Построить (табличным способом или в программе Excel) частотные характеристики элементов цепи R(f), X L(f), X C(f) и всей цепи в целом Z(f) в диапазоне частот 0 < f < 2f0 (рис. 2,2, б).
15. Построить зависимости I(f), UR(f), U L(f), U C(f) и провести их анализ в различных диапазонах частот (рис.2.2, в).
16. Построить фaзочастотную характеристику – зависимость сдвига фаз между напряжением U на клеммах генератора и током I в цепи от частоты f генератора: j(f) = arctg[(XL − XC)/R] (рис. 2.2, г).
17. Провести анализ полученных данных с точки зрения режима нагрузки (активно-индуктивная, активно-емкостная) при различных частотах. Объяснить, на каких частотах схема представляется активной, активно-емкостной, активно-индуктивной нагрузкой.
18. Построение векторной диаграммы токов и напряжений при различных режимах: при f < f0; f = f0; f >f0 описано в конспекте лекций и литературе.
Задача № 2.3
Комплексы действующих значений напряжения Ů k и тока İ k цепи (рис. 2.3) с комплексной нагрузкой Z k представлены в показательной и алгебраической форме в таблице 2.3. В каждом варианте представлено по два значения напряжения и тока (например, Ů1, İ1 и Ů2, İ2), записанных в соответствующей форме. Соответственно, каждому варианту соответствует комплексная нагрузка, например, Z k, имеющая активную ReZk и реактивную ImZk составляющие. На этой нагрузке выделяются мощности: полная комплексная S k, активная Pk и реактивная Qk.
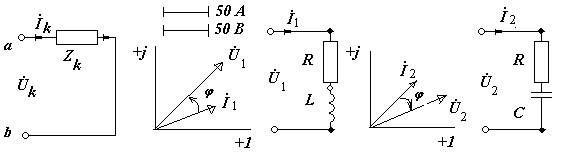
а) б) в) г) д)
Рис. 2.3. Схемы и векторные диаграммы к задаче № 2.3
Таблица 2.3
Задание к задаче № 2.3
| Параметр
| Последняя цифра номера зачетки | Пример | ||||||||||
| 0 | 1 | 2 | 3 | 4 | ||||||||
| t | n | t | n | t | n | t | n | t | n | t | n | |
| Ů1, B | 50 | 70 | 60 | 80 | 1 | 40 | 80 | 5 | 30 | 40 | 70 | 80 |
| İ1, A | 15 | 50 | 60 | 15 | 10 | 1 | 40 | 80 | 40 | 35 | 35 | 20 |
| Ů2, B | 90 | 10 | 50 | 25 | 25 | 35 | 70 | 10 | 80 | 75 | 70 | 30 |
| İ2, A | 10 | 20 | 50 | 10 | 35 | 10 | 35 | 5 | 1 | 15 | 40 | 50 |
|
| Последняя цифра номера зачетки | |||||||||||
| 5 | 6 | 7 | 8 | 9 | ||||||||
| t | n | t | n | t | n | T | n | t | n | |||
| Ů3, B | 60 | 20 | 40 | 20 | 80 | 70 | 15 | 55 | 60 | 25 | cм. U1 | |
| İ3, A | 50 | 15 | 60 | 15 | 40 | 80 | 10 | 25 | 1 | 40 | cм. I1 | |
| Ů4, B | 80 | 35 | 35 | 60 | 90 | 10 | 40 | 10 | 15 | 30 | cм. U2 | |
| İ4, A | 15 | 35 | 10 | 45 | 20 | 15 | 15 | 15 | 5 | 20 | cм. I2 | |
| Выбор условия варианта: Ů1 = t + jn; İ1 = t + jn; Ů3 = t + jn; İ3 = t + jn; Ů2 = te jn; İ2 = t + jn; Ů4 = te jn; İ4 = t + jn. | ||||||||||||
Необходимо рассчитать значения:
- действующих значений напряжений Uk и тока Ik;
- начальные фазы напряжения yUk и тока yIk, сдвиг фаз между током и напряжением jk = yUk - yIk, град;
- комплексное сопротивление Zk в алгебраической и показательной формах;
- активные ReZk и реактивные ImZk составляющие комплексных сопротивлений нагрузки Zk;
- полные S k в алгебраической и показательной формах, активные Pk, и реактивные Qk мощности;
- параметры схемы для построения векторной диаграммы для исследуемой цепи;
- нарисовать схему замещения для исследуемого варианта.
Для электрической схемы, соответствующей номеру варианта, выполнить следующие этапы расчета.
1. Записать задание, соответствующее номеру варианта
Ů1= 70 + j80, В; İ1 = 35 + j20, A; Ů2 = 70e j30, В; İ2 = 40+ j50, A.
2. Определить (рассчитать) параметры цепи.
3. Цепь с напряжением Ů1 и İ1.
4. Комплексное напряжение Ů1 в алгебраической форме:
Ů1 = 70 + j80 В.
5. Комплексное напряжение Ů1 в показательной форме:
Ů1 = Ue jyu1 = (t2+n2)0,5exp[jarctg(n/t)]; Ů1 = 106,3е j48,84 В.
6. Комплексный ток İ1 в алгебраической форме: İ1 = 35+ j20 A.
7. Комплексный ток İ1 в показательной форме:
İ1 = Ie jyi1 = (t2 + n2)0,5exp[jarctg(n/t)]; İ1 = 40,3е j29,75 A.
8. Угол сдвига фазы j = Dj1 между напряжением Ů1 и током İ1:
j = Dj1= yU1- yI1; j = 19,08 град.
9. Величина комплексного сопротивления Z1:
Zk = Ů k/İ k = Ue jyu/Ie jyI = (U/I)e jj = Ze jj = Zcosj + jZsinj = ReZ + jImZ;
Z1 = 2,49 + j0,862 Ом.
10. Величина активной составляющей комплексного сопротивления Z1: Re Z1 = 2,49 Ом.
11. Величина мнимой составляющей комплексного сопротивления Z1:
Im Z1 = 0,862 Ом.
12. Полная комплексная мощность S1:
S1 = Ů1İ1* = Se jj = U1i1e jj =Р1 + jQ1, где İ1* − комплексно-сопряженный ток İ1;
S1= 106,3е j48,84 40,3е −j29,75 = 4285е j19,1 = 4050 + j1400 ВА.
13. Активная мощность Р1: Р1 = U1I1cosj; Р1= 4050 Вт.
14. Реактивная мощность Q1: Q1= U1I1sinj; Q1= 1400 ВАр.
15 Построение векторной диаграммы токов и напряжений для исследуемой цепи. Векторная диаграмма строится по следующим этапам:
- выбираем масштабы для векторов напряжения и тока (рис. 2.3, б), например, 1см - 50 А; 1 см - 50 В;
− рисуем оси +1 и +j (ось +j направляем, например, вверх);
- на комплексной плоскости отмечаем точку, от которой будем строить вектора напряжений и токов (этой точке соответствует точка а схемы);
- поскольку в задаче задается значения вектора тока İ1, то строим его в выбранном масштабе токов с помощью транспортира под углом 29,75 о к оси +1;
- поскольку в задаче задается значения вектора напряжения Ů1, то строим его в выбранном масштабе напряжений под углом 48,84 о к оси +1;
- определяем, чему равен угол j между этими векторами: j =+19,08 о.
16. Рисуем схему замещения для исследуемого варианта. Поскольку вектор Ů1 опережает вектор İ1 на угол 19,08 о, то делаем вывод, что нагрузка активно-индуктивная, т.е. содержит идеальную индуктивность и резистор (рис. 2.3, в).
17. Цепь с напряжением Ů2 и İ2.
18. Комплексное напряжение Ů2 в показательной форме: Ů2 = 70e j30 В.
19. Комплексное напряжение Ů2 в алгебраической форме:
Ů2 = 60,6 + j35 В.
20. Комплексный ток İ2 в алгебраической форме: I2 = 40 + j50 A.
21. Комплексный ток İ2 в показательной форме: İ2 = 64е j51 A.
22. Угол сдвига фазы j = Dj2 между напряжением Ů2 и током İ2:
j = Dj2 = yU2 - yI2; j = −21,37 град.
23. Величина комплексного сопротивления Z2:
Zk = Ů k/İ k = Ue jju/Ie jji = (U/I)e jj = Ze jj =Zcosj + jZsinj = ReZ + jImZ;
Z2 = 1,02 - j0,39 Ом.
24. Величина активной составляющей комплексного сопротивления Z2:
Re Z2 = 1,02 Ом.
25. Величина мнимой составляющей комплексного сопротивления Z2:
Im Z2 = - 0,39 Ом.
26. Полная комплексная мощность S2:
S2= Ů2İ* = S2e jj = U2I2 e jj = Р2 + jQ2,
где İ2* − комплексно-сопряженный ток İ2;
S2 = 70e j3064е −j51 = 4482е- j21= 4174 - j1632 ВА.
27. Активная мощность Р2: Р2 = U2i2cosj; Р2 = 4171 Вт.
28. Реактивная мощность Q2: Q2= U2i2sinj; Q2 = -1632 вАр.
29. Построим векторную диаграмму токов и напряжений для исследуемой цепи (рис. 2.3, г, д). Нагрузка - активно-емкостная.
30. Рисуем схему замещения для исследуемого варианта.
Задача № 2.4
Для цепи, схема которой представлена на рис. 2.4, а, заданы действующее напряжение Ůa d, сопротивления R1, X1, R2, X2, R0, X0 (табл. 2.4). Начальную фазу yUad напряжения Ůа d схемы принять равной нулю.
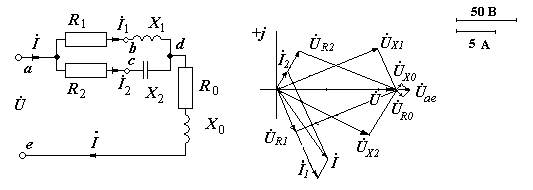
а) б)
Рис. 2.4. Схема (а) и векторные диаграммы напряжения и токов (б) к задаче № 2.4
С учетом параметров схемы необходимо определить (рассчитать):
- комплексные токи İ1, İ2, İ;
- комплексное напряжение Ů bc между точками b и c схемы, комплексное напряжение на входе Ůае;
- параметры схемы для построения векторной диаграммы напряжений и токов для исследуемой цепи.
Таблица 2.4.
Задание к задаче № 2.4
| Параметры | Последняя цифра номера зачетки | Пример | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Ua d, B | 220 | 380 | 127 | 660 | 220 | 380 | 127 | 660 | 220 | 380 | 127 |
| R1, Ом | 5 | 6 | 7 | 8 | 9 | 10 | 9 | 8 | 7 | 6 | 5 |
| X1, Ом | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 6 | 7 | 8 |
| Предпоследняя цифра номера зачетки | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| R2, Ом | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| X2, Ом | 45 | 44 | 43 | 42 | 41 | 40 | 39 | 38 | 37 | 35 | 35 |
| R 0, Ом | 2 | 1,9 | 1,8 | 1,7 | 1,6 | 1,5 | 1,4 | 1,3 | 1,2 | 1,1 | 1 |
| X 0, Ом | 3 | 2,8 | 2,6 | 2,4 | 2,2 | 2,0 | 1,8 | 1,6 | 1,4 | 1,2 | 1 |
Для электрической схемы, соответствующей номеру варианта, выполнить следующие этапы расчета.
1. Зарисовать схему и записать задание, соответствующее номеру варианта (рис. 2.4, а; табл. 2.4).
2. Определить (рассчитать) параметры схемы.
3. Комплексные сопротивления резистивных элементов цепи в алгебраической форме:
Z(R) = R + j0; Z(R0) = 1 + j0 Ом; Z(R1) = 5 + j0 Ом; Z(R2) = 20 + j0 Ом.
4. Комплексные сопротивления индуктивных элементов цепи в алгебраической форме: Z(L) = 0 + jXL; Z(Х0) = 0 + j1 Ом; Z(Х1) = 0 + j8 Ом.
5. Комплексные сопротивления емкостных элементов цепи в алгебраической форме: Z(C) = 0 - jXC; Z(Х2) = 0 - j35 Ом.
6. Комплексные сопротивления участков цепи в алгебраической форме:
Z jk = Z j + Z k; Z abd = Z11= 5+ j8 Ом; Z acd = Z22=20- j35 Ом; Z de = Z00=1 + j1 Ом.
7. Комплексное сопротивление участка цепи между точками ad в показательной и алгебраической формах:
Z ad =(Z11Z22)/(Z11 + Z22); Z ad =10,3e j45 = 7,31 + j7,30 Ом.
8. Комплексное сопротивление всей цепи между точками ae в показательной и алгебраической формах: Z a е = Z ad + Z00; Z a е = 11,75e j44,95 = 8,315 + j8,3 Ом.
9. Комплекс действующего тока İ1 в ветви на участке ad:
İ1 = Ůad/Z11; İ1 = 13,5e-j58 = 7,135 - j11,42 A.
10. Комплекс действующего тока İ2 в ветви на участке ad:
İ2 = Ůad/Z22; İ2 = 3,2e j 60,3 = 1,56 + j2,73 A.
11. Комплекс действующего значения тока İ (комплексный ток) на участке ad c учетом yUad = 0: İ = İ1 + İ2; İ = 12,29e- j44,95 = 8,698 - j8,680 A.
12. Комплекс действующего значения напряжения Ůае, приложенного к входу цепи ае: Ůае = İ Z ae; Ůае = 144e- j 0,07 = 144,4 + j0,0176 B.
13. Комплексное напряжение Ů1 на резисторе R1:
Ů1 = İ1R1; Ů1 = 67,31e- j57,99 = 35,67 - j57,08 B.
14. Комплексное напряжение Ů2 на резисторе R2:
Ů2 = İ2R2; Ů2 = 63,01e j 60 = 31,26 + j54,71 B.
15. Комплексное напряжение Ů bc между точками b и c схемы:
Ů bc = İ2R2 - İ1R1; Ů bc = -4,42 + j111,77 = 111,9e j92,28 В.








