Коэффициент корреляции
Коэффициент корреляции - это величина, которая может варьировать в пределах от 4-1 до — 1. В случае полной положительной корреляции этот коэффициент равен плюс 1, а при полной отрицательной - минус 1. На графике этому соответствует прямая линия, проходящая через точки пересечения значений каждой пары данных:
Переменная
А
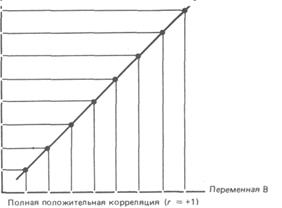
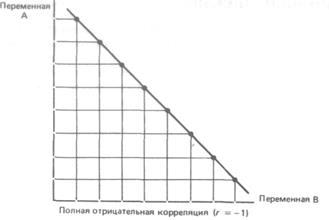
В случае же если эти точки не выстраиваются по прямой линии, а образуют «облако», коэффициент корреляции по абсолютной величине становится меньше единицы и по мере округления этого облака приближается к нулю:
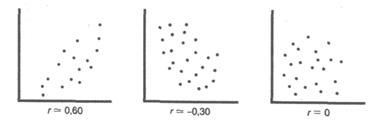
В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.
В гуманитарных науках корреляция считается сильной, если ее коэффициент выше 0,60; если же он превышает 0,90, то корреляция считается очень сильной. Однако для того, чтобы можно было делать выводы о связях между переменными, большое значение имеет объем выборки: чем выборка больше, тем достовернее величина полученного коэффициента корреляции. Существуют таблицы с критическими значениями коэффициента корреляции Браве-Пирсона и Спирмена для разного числа степеней свободы (оно равно числу пар за вычетом 2, т. е. n-2). Лишь в том случае, если коэффициенты корреляции больше этих критических значений, они могут считаться достоверными. Так, для того чтобы коэффициент корреляции 0,70 был достоверным, в анализ должно быть взято не меньше 8 пар данных (h = п - 2 = 6) при вычислении r (табл. В.4) и 7 пар данных (h = п - 2 = 5) при вычислении rs (табл. 5 в дополнении Б. 5).
Коэффициент Браве – Пирсона
Для вычисления этого коэффициента применяют следующую формулу (у разных авторов она может выглядеть по-разному):
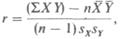
где åXY - сумма произведений данных из каждой пары;
n - число пар;
- средняя для данных переменной X ;
- средняя для данных переменной Y;
S Х - стандартное отклонение для распределения x;
sY - стандартное отклонение для распределения у.
Теперь мы можем использовать этот коэффициент для того, чтобы установить, существует ли связь между временем реакции испытуемых и эффективностью их действий. Возьмем, например, фоновый уровень контрольной группы.

n= 15 × 15,8 × 13,4 = 3175,8;
(n – 1)SxSy = 14 × 3,07 × 2,29 = 98,42;
r = 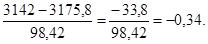
Отрицательное значение коэффициента корреляции может означать, что чем больше время реакции, тем ниже эффективность. Однако величина его слишком мала для того, чтобы можно было говорить о достоверной связи между этим двумя переменными.
Теперь попробуйте самостоятельно подсчитать коэффициент корреляции для экспериментальной группы после воздействия, зная, что åХУ= 2953:
nXY=………
(n - 1)SXSY =……
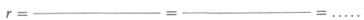
Какой вывод можно сделать из этих результатов? Если вы считаете, что между переменными есть связь, то какова она - прямая или обратная? Достоверна ли она [см. табл. 4 (в дополнении Б. 5) с критическими значениями r]?








