Свойства решений линейных д.у. n -го порядка.

Дата: 2025-05-25; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

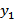1) если и 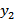решения однородного д.у., то для любого α,β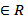 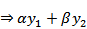– тоже решенияд.у. 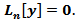Док-во. 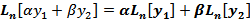=0 следствие решения линейного однородного д.у. образуют линейное пространство.

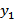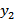2) если и -решения 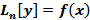то их разность равна нулю.Док-во: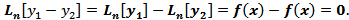

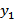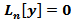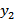3)если решение . , а решение 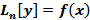то их сумма решение 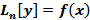.Док-во: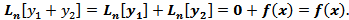

Вопрос 24

(Сформулировать определения линейно зависимой и линейно независимой систем функций)

1) Система функций 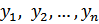называется линейно зависимой на (a , b), если существуют такие числа 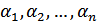,из которых хотя бы одно отлично от нуля, что для любогоx (a , b ) имеет место равенство: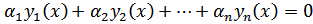

Замечание: Если заданы две функци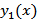и и 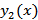то их линейная зависимость равносильна условию пропорциональности этих функций: 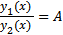, где A- некоторая постоянная.

2) Система функций 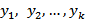называется линейно независимой на (a , b), если равенство 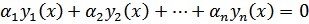имеет место для x 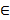(a , b ) только тогда, когда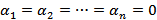

Замечание:При задании двух линейно независимых функци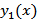й и 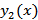, их отношением будет некоторая функция, не являющаяся постоянной: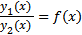

(Сформулировать и доказать теорему о вронскиане линейно зависимых функций)

Если система функций 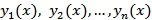линейно зависима на интервале (a, b), то вронскиан этой системы тождественно равен нулю на этом интервале.

- Доказательство:

Если функции 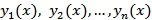линейно зависимы на интервале (a, b), то найдутся числа 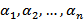, из которых хотя бы одно отлично от нуля, такие что 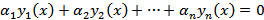для любого x 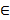(a , b ) (1)

Продифференцируем по x равенство (1) n - 1 раз и составим систему уравнений:

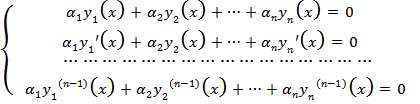
Будем рассматривать эту систему как однородную линейную систему алгебраических уравнений относительно 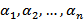. Определитель этой системы - определитель Вронского (2). При любом x 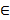(a , b ) эта система имеет нетривиальное решение 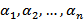, следовательно, в каждой точке её определитель равен нулю. Итак, W (x) = 0 при любом x 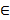(a , b ), т.е. W(x) = 0 на (a, b).

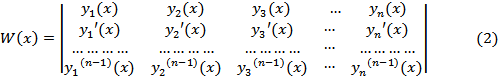
Вопрос 25

(Сформулировать определение линейно зависимой и линейно независимой систем функций. Сформулировать и доказать теорему о вронскиане системы линейно независимых частных решений линейного однородного дифференциального уравнения n - го порядка)

1) Система функций 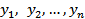называется линейно зависимой на (a , b), если существуют такие числа 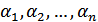,из которых хотя бы одно отлично от нуля, что для любого x 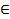(a , b ) имеет место равенство: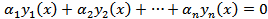

2) Система функций 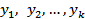называется линейно независимой на (a , b), если равенство 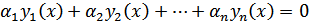имеет место для x 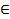(a , b ) только тогда, когда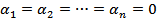

Определителем Вронского называется определитель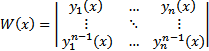

-Теорема:

Пусть 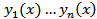решение ДУ 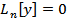с непрерывными коэффициентами. Чтобы эти функции были линейно независимы на (а, b)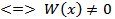

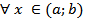
-Доказательство:

Допустим противное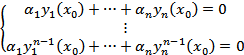

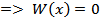
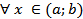
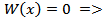СЛАУ имеет нетривиальное решение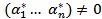

Рассмотрим 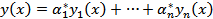- решение ДУ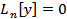

Примем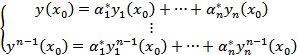

Задача Коши 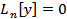, , 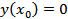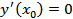… имеет единственное решение 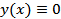. 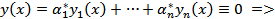Система линейно независима. Противоречие!

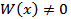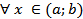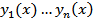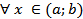
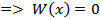
Пусть для . Предположим, что решение линейно зависимо для 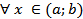. Противоречие! Теорема доказана.

Вопрос 26

(Сформулировать и доказать теорему о существовании фундаментальной системы решений линейного однородного дифференциального уравнения n - го порядка)

Систему из n линейно независимых решений ЛОДУ 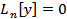называется ФСР этого ДУ

-Теорема:

Для ДУ 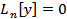с непрерывными коэффициентами 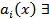ФСР.

-Доказательство:

Пусть 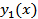решение задачи Коши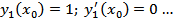

Пусть 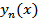решение задачи Коши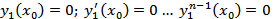

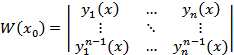= =1 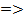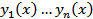линейно независимые.

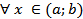выполняются условия теоремы Коши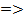 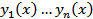ФСР ДУ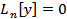

Теорема доказана.

Вопрос 27

-Теорема:

Пусть 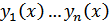ФСР ЛОДУ 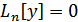с непрерывными коэффициентами , .

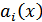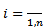Тогда общее решение ДУ имеет вид
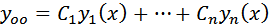, где 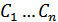произвольные константы.

-Доказательство:

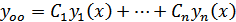
Пусть 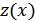-решение задачи Коши для …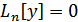

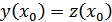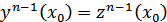
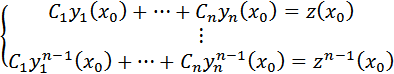
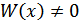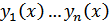(т.к. ФСР) 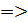СЛАУ имеет единственное решение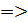 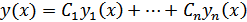удовлетворяет тем же начальным условиям, что и 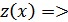согласно теореме Коши .

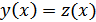Теорема доказана.

Вопрос 28

(Вывести формулу О строградского -Л иувилля для линейного дифференциального уравнения 2- го порядка)

Формула Лиуви́лля-Острогра́дского — формула, связывающая определитель Вронского (вронскиа́н) для решений дифференциального уравнения и коэффициенты в этом уравнении.

Доказательство для уравнения второго порядка:

Пусть y1 = y1(x) и y2 = y2(x) – решения линейного однродного дифференциального уравнения второго порядка:

y” + p(x)y’ + q(x)y = 0

где p(x) и q(x) – функции, непрерывные на некотором промежутке. Для определителя Вронского указанных решений имеем

+

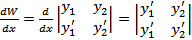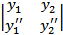
Первое слагаемое равно 0, так как этот определитель содержит 2 одинаковые строки. Подставив

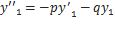
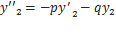
во второе слагаемое получим

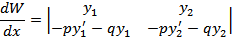
Домножим верхнюю строчку на q(x) и сложим со 2-й

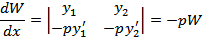
, т.е. W ’(x)+p(x)W(x)=0

Мы видим, что определитель Вронского W(x) удовлетворяет уравнению: y’ + p(x)y=0(5)

Непосредственной проверкой можно убедиться, что этому же уравнению удовлетворяет и функция:

y(x)=W(x₀)e ^{–S p(t)dt}

причём y(x0) = W(x0), где x0 – произвольная фиксированная точка промежутка I. Из теоремы существования и единственности для уравнения (5) получаем, что для всех x ∈ I выполняется равенство: W(x)=W(x₀)e ^{–S p(t)dt}

Это равенство называется формулой Остроградского-Лиувилля.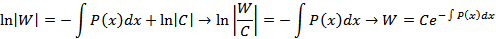

Вопрос 29

(Вывести формулу для общего решения линейного однородного дифференциального уравнения 2-го порядка при одном известном частном решении)

Дифференциальное уравнение второго порядка называется линейным, если оно первой степени (линейно) относительно искомой функции у и ее производных 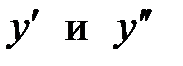. 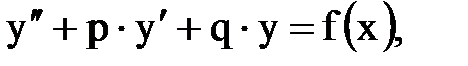где 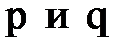– либо функции от х, либо постоянные. При f(x) = 0 уравнение называется линейным однородным. Общее решение линейного однородного дифференциального уравнения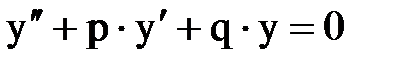

имеет вид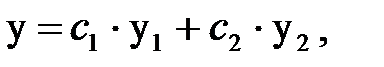

где 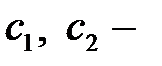две произвольные постоянные; 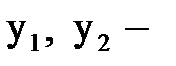два частных решения уравнения, линейно независимых. Заметим, что два решения: 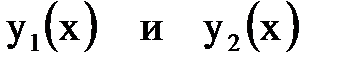– называются линейно независимыми, если их отношение не является постоянным, т. е.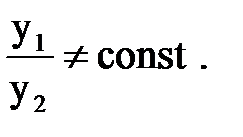

Доказательство:

Из равенства Остроградского-Лиувилля:

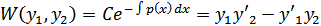то разделив это неравенство на y₁² , получим

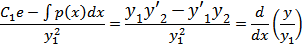
Уравнение с разделяющимися переменными, интеграл которого является общим решениям:

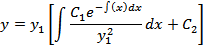
Вопрос 30

(Сформулировать и доказать теорему о структуре общего решения линейного неоднородного дифференциального уравнения n -го порядка)

Теорема: Пусть 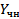- частное д.у. Ln[y]=F(x), и 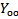- общее решение однородного д.у. Ln[y]=F(x). Тогда общее решение уравнения 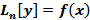имеет вид 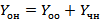.Любое решение неоднородного д.у. можно представить в виде где 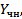– частное решение ур-я, а y ₁ ( x ), … , y_n ( x ) – ФСР соответствующего однородного уравнения; C ₁ , … , C_n – произвольные постоянные

Доказательство:

при всех значениях постоянных C ₁ , … , C_n является решением д.у. 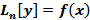(согласно теоремам о свойствах решений)Пусть z(x)- произвольное решение д.у. 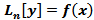.Так как z(x) и 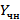– решения неоднородного д.у. 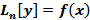, то их разность –есть решение однородного д.у. 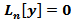(согласно теореме о свойствах решений)Тогда согласно теореме о структуре общего решения линейного однородного д.у. 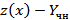= , где C ₁ , … , C_n – произвольные постоянные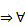

Решение представленное в таком виде .

Вопрос 31, 32

(Вывести формулу для общего решения линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами в случае кратных и комплексных корней характеристического уравнения)

Линейное однородное дифференциальное уравнение с постоянными коэффициентами имеет вид 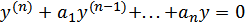где a₁...a_n – вещественные числа. Уравнение:

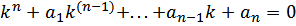называется характеристическим уравнением дифференциального уравнения. Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами имеет вид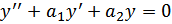

Напишем соответствующее характеристическое уравнение: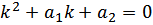

Для хар. уравнения возможен один (и только один) из следующих случаев:1) Корни уравнения (3) вещественны и различны. Обозначим эти корни k ₁ и k ₂. Тогда 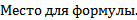фундаментальную систему решений уравнения (2) образуют функци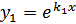и: и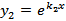

а общее решение имеет вид 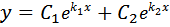Здесь нужно проверить лишь линейную независимость решений y₁ и y₂; чтобы убедиться в этом, составим определитель Вронского:

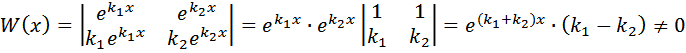
Таким образом, y₁ и y₂ линейно независимы и, следовательно, образуют фундаментальную

систему решений уравнения (2).

2) Уравнение (3) имеет один вещественный корень кратности 2; обозначим этот корень k ₀. Тогда фундаментальную систему решений уравнения (2) образуют функци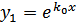и и 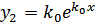, а общее решение этого уравнения есть 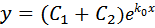Проверим, что y₂ есть решение уравнения (2). Т.к. k ₀ - корень кратности 2 характеристического уравнения (3), то 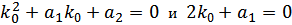Далее: 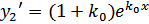и 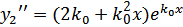Отсюда: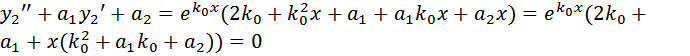

т.е. y ₂ – решение уравнения (2). Проверим линейную независимость y₁ и y₂ :

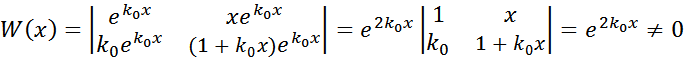
Таким образом, y₁ и y₂ образуют фундаментальную систему решений уравнения (2).

3) Характеристическое уравнение имеет комплексно сопряженные корни λ_1,2 = α ± i β, β ≠ 0. В этом случае фундаментальная система решений уравнения (2) имеет вид 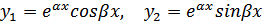а общее решение записывается так: 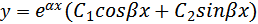Здесь в проверке нуждается лишь линейная независимость решений y₁ и y₂; имеем

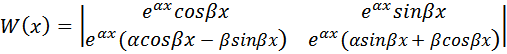
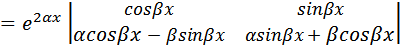
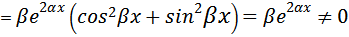
Поэтому y₁ и y₂ линейно независимы

Вопрос 33

(Частное решение ЛНДУ с постоянными коэффициентами и правой частью специального вида (являющейся квазимногочленом). Сформулировать и доказать теорему о наложении частных решений)

-Теорема (о наложении частных решений):

Пусть имеются два линейных неоднородных уравнения:
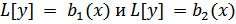где
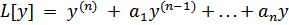и пусть y₁ = y₁(x) и y₂ = y₂(x) – решения этих уравнений. Тогда y₁(x) + y₂(x) будет решением уравнения L[y] = b₁(x) + b₂(x).

-Доказательство:

Имеем
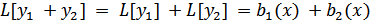т.е. y₁ +y₂ – решение уравнения L[y] = b₁(x) + b₂(x).

Теорема доказана.

Квазимногочленом называется сумма нескольких слагаемых вида:

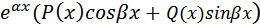
где P(x) и Q(x) – многочлены.

Частное решение линейного неоднородного уравнения с постоянными коэффициентами : L[y] = b(x)

и квазимногочленом в правой части рекомендуется искать методом неопределённых коэффициентов (методом подбора). Для каждого слагаемого данного вида, входящего в правую часть решаемого уравнения, частное решение уравнения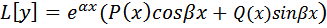

ищется в виде:

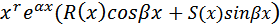
где r = 0, если α+i β не есть корень характеристического уравнения, и r равно кратности этого корня в противном случае; R(x) и S(x) – многочлены с неопределёнными коэффициентами, степень каждого из которых равна максимальной из степеней P(x) и Q(x). Для нахождения неопределённых коэффициентов выражение (8) подставляется в соответствующее уравнение, и затем приравниваются коэффициенты при подобных членах слева и справа. После того, как частные решения найдены для всех слагаемых, входящих в b ( x ), частное решение исходного уравнения определяется с помощью теоремы о наложении решений.

Вопрос 34

( Метод Лагранжа вариации постоянных для нахождения решения ЛНДУ 2-го порядка)

-Определение:

Линейное неоднородное дифференциальное уравнение n-го порядка имеет вид

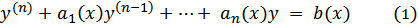
-Метод Лагранжа (вариации постоянных):

Пусть y₁ = y₁(x), ..., y_n = y_n(x) – фундаментальная система решений однородного уравнения L[y] = 0. Тогда частное решение неоднородного уравнения L[y] = b(x) можно искать в виде

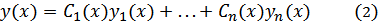
где функции C₁ = С₁(x), ..., C_n = C_n(x) определяются из системы

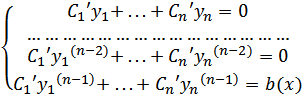
Так как определитель

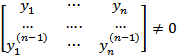
то из этой системы C'₁, ..., C'_n определяются однозначно, а сами функции C₁, ..., C_n – с точностью до произвольных постоянных. Если в (2) подставить именно эти функции

C₁ = C₁(x), ..., C_n = C_n(x), то получим частное решение уравнения (1).

-Метод Лагранжа для функции второго порядка (n=2):

Уравнение в этом случае имеет вид

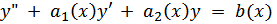
где a₁(x), a₂(x), b(x) – непрерывные на некотором промежутке функции. Частное решение

данного уравнения ищем в виде

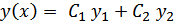
где y₁(x), y₂(x)– фундаментальная система решений однородного уравнения

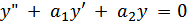
a C₁ = C₁(x) и C₂ = C₂(x) – подлежащие определению функции. Предположим, что они удовлетворяют системе:

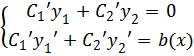
Тогда

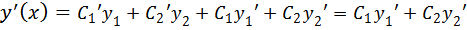
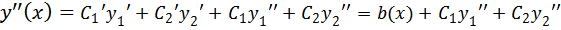
Отсюда

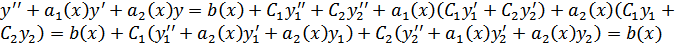
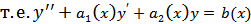– что и требовалось доказать!

Вопрос 35

(Сформулировать определение дифференциального уравнения n -го порядка, разрешенного относительно старшей производной, и сформулировать задачу Коши для такого уравнения. Описать метод сведения этого уравнения к нормальной системе ду)

Всякую систему, в которой уравнения разрешены относительно старших производных, а число уравнений равно числу неизвестных, можно с помощью введения новых неизвестных функций свести к нормальной системе. Рассмотрим соответствующий прием для системы из двух уравнений:

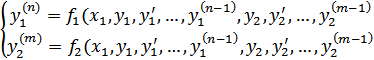
Пусть y₁₁ = y₁, y₁₂ = y’₁, ..., y_1n = y₁^(n-1), y₂₁ = y₂, y₂₂ = y’₂, ..., y_2m = y₂^(m-1). Относительно

этих функций получаем такую (нормальную) систему:

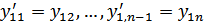
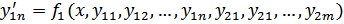
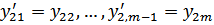
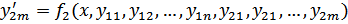
Ясно, что одно уравнение n -го порядка этим приемом будет сведено к нормальной системе относительно n неизвестных функций. В принципе верно и обратное: при определенных условиях нормальную систему можно свести к одному уравнению. Пусть имеется нормальная система двух уравнений

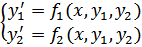
Продифференцируем по x первое уравнение и подставим в получившееся выражение вместо y’₂, правую часть второго уравнения системы:

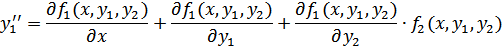
Затем из первого уравнения системы определим y₂ как функцию x, y₁, y’₁, т.е. y₂ = y₂(x, y₁, y’₁) и поставим эту функцию вместо y₂ в полученное ранее равенство. Т.о., следствием данной системы является уравнение второго порядка относительно одной неизвестной функции y₁ = y₁(x). Аналогичным приемом можно получить и уравнение относительно y₂ = y₂(x).

Вопрос 36

(Сформулировать задачу Коши для нормальной системы дифференциальных уравнений и теорему Коши о существовании и единственности решения этой задачи. Описать метод сведения нормальной системы к одному дифференциальному уравнению высшего порядка)

-Определение:

Нормальной системой обыкновенных дифференциальных уравнений n-го порядка называется система вида

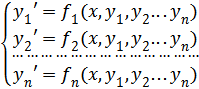
или

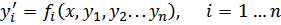
-Определение:

Задача Коши для Нормальной системой обыкновенных дифференциальных уравнений n-го порядка ставится следующим образом. Дана точка (x₀, y₁₀, ..., y_n0), принадлежащая области определения правых частей этой системы; требуется найти решение y_i=y_i(x), i=1, …, n удовлетворяющее начальным условиям y_i(x₀)=y_i0 , i=1, ..., n.

-Теорема (Коши существования и единственности для нормальной системы): Пусть правые части системы

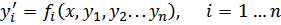
определены, непрерывны и имеют непрерывные частные производные по переменным y₁ ,... ,y_n в некоторой области G 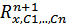. Тогда для любой точки (x₀, y₁₀, ..., y_n0) G существует решение данной системы, удовлетворяющее начальным условиям y_i'(x₀)=y_i0, i=1, ..., n. Любые два решения этой системы, удовлетворяющие одним и тем же начальным условиям, совпадают всюду, где они оба определены. Без доказательства.

Вопрос 37

(Сформулировать определение первого интеграла нормальной системы дифференциальных уравнений. Описать методы нахождения первых интегралов и их применение для решения системы дифференциальных уравнений)

-Определение:

Функцию u(x)=u(X₁,X₂,...,X_n), определённую и непрерывную вместе со своими частными производными в некоторой области D изменения фазовых переменных X₁,X₂,...,X_n называют первым интегралом системы dx/dt =f(x)(где x(t)=(X₁(t),X₂(t),...,X_n(t)) - вектор-функция скалярного аргумента t с координатными функциями X_i (t), определёнными в некотором промежутке Т ⊆ R числовой прямой R, а f(x)=(f₁(x),...,f_n(x)) - векторная функция векторного аргумента x с координатными функциями f_i(x), i=1,n ,определёнными и непрерывно дифференцируемыми в некоторой области D ⊆ R n-мерного фазового пространства в области D ,если при подстановке в u(x) произвольного решения x=g(t) этой системы ,траектория которого целиком расположена в D ,получим постоянную относительно t величину. Иными словами, функция u(g(t)) зависит только от выбора решения g(t), но не от независимого переменного t.

-Теорема:

Для того, чтобы функция u(x) была первым интегралом системы dx/dt =f(x), необходимо и достаточно, чтобы она удовлетворяла в области D соотношению:

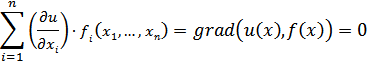
-Доказательство:

Пусть u(x) - первый интеграл системы dx/dt =f(x). Рассмотрим произвольную точку x₀ ∈ D. Если x(t)=g(t) - решение системы dx/dt =f(x), удовлетворяющее начальному условию g(t₀) = x₀ ∈ D, то, согласно определению первого интеграла, V(t) = u(g(t)) = const и dV/dt=0. В соответствии с 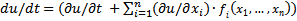, производная dV/dt совпадает с полной производной по t функции u(x) в силу системы dx/dt =f(x) на решение g(t).Поэтому в точке x₀ : du/dt = dV/dt =0

т.е. в области D выполнено равенство:

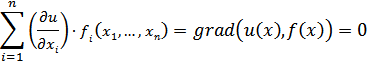
Докажем обратное утверждение. Пусть выполнено: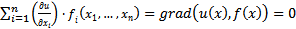

и x(t)=g(t) - решение системы dx/dt =f(x), фазовая траектория которого лежит в D, тогда с учето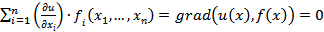м имеем

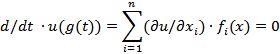
т.е. u(g(t)) не зависит от t и, следовательно, в соответствии с определением dx/dt =f(x), u(x)-первый интеграл системы dx/dt =f(x).

-Геометрический смысл:

условие 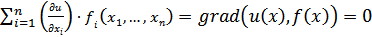имеет простой геометрический смысл. В любой точке x ∈ D вектор grad(u(X)) градиента скалярной функции u(x) ортогонален к ее поверхности уровня S, задаваемой уравнением u(x)=u( X ) . Из равенства следует, что в каждой точке X ∈ S вектор f( x ) касается этой поверхности. Поэтому фазовая траектория, проходящая через точку X ∈ S, лежит на поверхности S.