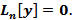Для вычисления площади криволинейного сектора рассмотрим разбиение отрезка [α, β] и предположив, что r( ) непрерывна на рассматриваемом отрезке, напишем очевидное неравенство

Дата: 2025-05-25; Просмотры: 3
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

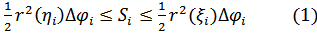в котором Si − площадь криволинейного сектора, отвечающего изменению 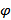на отрезке [ 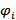−1, 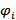]; r(ηi) и r(ξi) − соответственно наименьшее и наибольшее значения функции r( 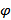) на указанном частичном отрезке разбиении; при составлении неравенства (1) была использована известная школьная формула для площади криволинейного сектора. Кроме того, мы предполагаем дополнительно, что r( 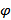) непрерывна на отрезке [α, β]. Суммируя неравенства (1) по i = 1, 2, ..., n получим, что для площади S рассматриваемого криволинейного сектора справедливо неравенство 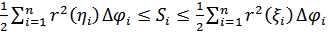Переходя здесь к пределу при 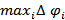→ 0, получаем требуемую формулу: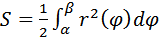

Вопрос 18

(Тело образовано вращением вокруг оси Ox криволинейной трапеции, ограниченной кривой y = f ( x ) ≥ 0, прямыми x = a , x = b и y = 0 ( a < b ) . Вывести формулу для вычисления с помощью определенного интеграла объема тела вращения)

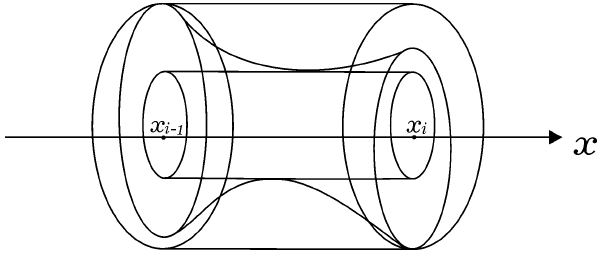
Определенные интегралы можно применять и для вычисления объемов. Пусть тело M заключено между плоскостями x = a и x = b, и пусть для каждой точки x ∈ [a, b] известна площадь S(x) фигуры, получающейся в сечении тела M плоскостью, перпендикулярной оси абсцисс и проходящей через указанную точку. Предположим далее, что проекции двух сечений тела M такими плоскостями на плоскость OYZ лежат одна в другой (во всяком случае, для сечений, отвечающих достаточно близким плоскостям). Разобьем отрезок [a, b] на части точками Тогда объем Vi части Mi тела, расположенной между плоскостями x = xi−1 и x = xi в силу сделанного выше предположения о проекциях сечений тела M при достаточно малом диаметре разбиения удовлетворяет неравенству 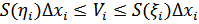где S ( ηi ) и S ( ξi ) − соответственно минимальное и максимальное значение функции S ( x ) на отрезке [xi −1, xi]; здесь мы предполагаем дополнительно, что S ( x ) непрерывна на [a , b] Геометрический смысл величин S(ηi)∆xi и S(ξi)∆xi очевиден - это объемы прямых круговых цилиндров, один из которых содержится в части Mi тела M, а другой содержит внутри себя эту часть. Переходя в этом неравенстве к пределу при maxi∆xi →0, получим неравенство 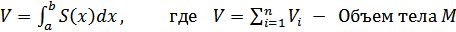Если тело M получено вращением графика непрерывной функции y = f(x), a ≤ x ≤ b, то, очевидно,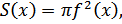

и мы получаем такую формулу для вычисления объема тела вращения: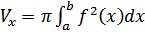

Вопрос 19

(Кривая задана в декартовых координатах уравнением y = f ( x ), где x и y – декартовые координаты точки, a ≤ x ≤ b . Вывести формулу для вычисления длины дуги этой кривой)

Непрерывно дифференцируемая плоская кривая Γ спрямляема, и производная S’(t) переменной длины дуги вычисляется по формуле: 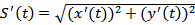Т.к. одной из первообразных функции из правой части этого равенства является 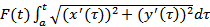то отсюда, поскольку F(a) = 0, следует равенство: 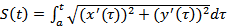Поэтому для длины всей кривой имеем формулу: 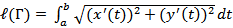Если кривая Γ задана явно уравнением y = y ( t ), a ≤ x ≤ b, то, беря x в качестве параметра, получаем такую формулу: 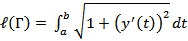для длины пространственной кривой Γ, заданной уравнениями x = x ( t ), y = y ( t ), z = z ( t )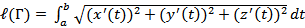

Вопрос 20

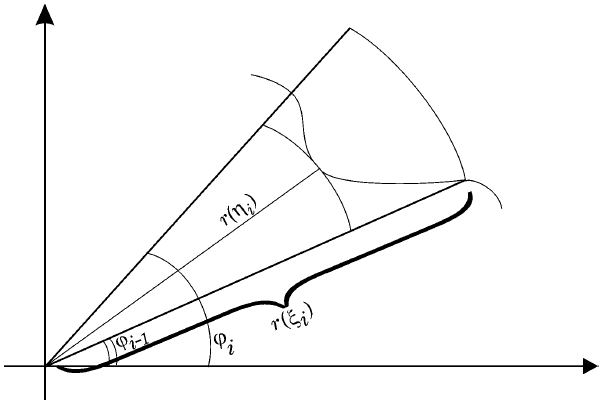
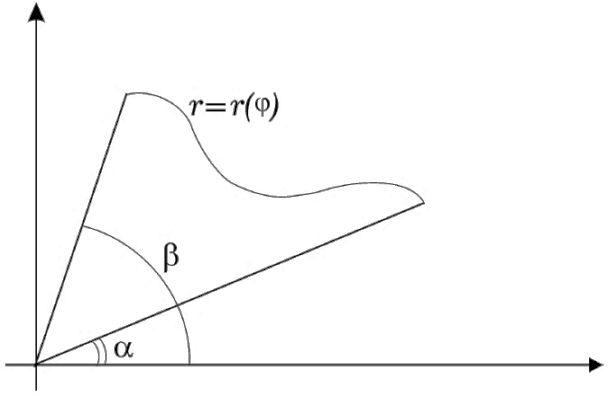
(Кривая задана в полярных координатах уравнением r = r ( 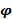) ≥ 0 , где r и 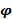– полярные координаты точки, α < 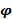< β. Вывести формулу для вычисления длины дуги этой кривой)

Пусть кривая Γ задана в полярных координатах:

Тогда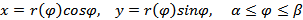

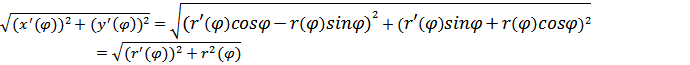
Поэтому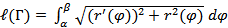

Вопрос 21

(Линейные дифференциальные уравнения 1-го порядка. Интегрирование линейных неоднородных дифференциальных уравнений 1-го порядка методом Бернулли (метод “ uv ”) и методом Лагранжа (вариации произвольной постоянной))

1)К линейным уравнениям первого порядка сводится уравнение Бернулли

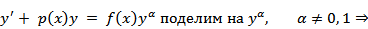
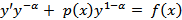
Если 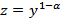, то 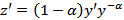, и относительно z имеем линейное уравнение:

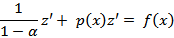
Решив его, найдем z, а затем и y. При α > 0 уравнению Бернулли удовлетворяет также функция, тождественно равная нулю. Другой подход к решению уравнений Бернулли состоит в следующем. Пусть y = u · v; тогда:

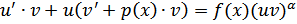
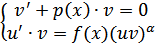
2)Уравнение вида: 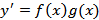называется уравнением с разделяющимися переменными

3) Уравнение 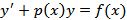называется линейным

функции p(x) и f(x) будем считать непрерывными на некотором интервале I. Чтобы решить уравнение, найдем сначала общее решение соответствующего однородного уравнения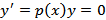

Пусть P(x) – какая-либо первообразная функции p(x) на интервале I. Тогда, как легко проверить, функция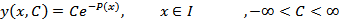

есть общее решение уравнения. Далее применим метод вариации постоянной, состоящий в том, что постоянная C, входящая в общее решение, заменяется функцией C ( x ); затем эта последняя функция определяется из исходного неоднородного уравнения. Имеем:

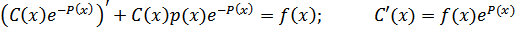
Отсюда 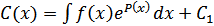где интеграл в правой части означает какую-любо фиксированную первообразную соответствующей функции (а не всю совокупность этих первообразных). Следовательно, общее решение уравнения имеет вид: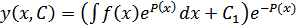

Вопрос 22

( Сформулировать теорему Коши о существовании и единственности решения дифференциального уравнения n -го порядка )

Задачей Коши для дифференциального уравнения 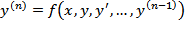называют задачу нахождения решения удовлетворяющую начальным условиям y( 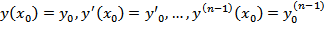где 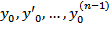заданные числа.

Теорема Коши(о существовании и единственности решения для дифференциального уравнения n-го порядка): Пусть в области D из R n+1 функция 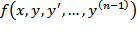непрерывна и имеет непрерывные частные производные y,y‘,…y(n-1). Тогда для любой точки (x0,y0,y0',…,y0(n-1)) D решение задачи y(n)=f(x,y,y’,…t(n-1)) .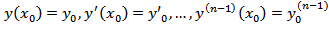

(Интегрирование дифференциальных уравнений n-го порядка, допускающих понижение порядка)

1) Уравнение вида 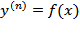. После n-кратного интегрирования получается общее решение

Y=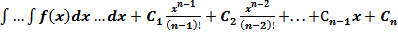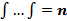

Где и где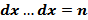

2) Уравнение не содержит искомой функции и её производных до порядка k-1 включительно: F(x,y(k),y(k+1),…,y(n))=0

Порядок такого уравнения можно понизить на 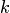единиц заменой y(k)(x)=p(x) . Тогда уравнение примет вид

F(x,p,p’,…,p(n-k))=0

Из последнего уравнения, если это возможно, определяем p=f(x,C1,C2,…..,Cn-k), а затем находим y из уравнения y(k)=f(x,C1,C2,…Cn-k) k-кратным интегрированием.

3) Уравнение не содержит независимого переменного:

F(y,y’y”,…,y(n))=0

Подстановка y’=p позволяет понизить порядок уравнения на единицу. При этом 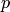рассматривается как новая неизвестная функция от y:p=p(y). Все производные y’,y”,…,y(n) выражаются через производные от новой неизвестной функции p по y

y’=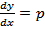

y”= =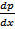

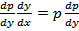
y”’= 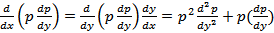2 etc

 

Подставив эти выражения вместо (y,y’y”,…,y(n)) в уравнение, получим дифференциальное уравнение (n–1)-го порядка.

Вопрос 23

(Сформулировать теорему Коши о существовании и единственности решения линейного дифференциального уравнения n-го порядка)

Пусть функция f(x), 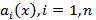непрерывна на промежутке T 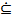R.Тогда для любой точки 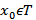и для любых чисел 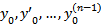решения задачи Коши 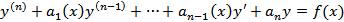существует и единственно.

(Доказать свойства частных решений линейного однородного дифференциального уравнения n-го порядка)

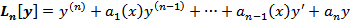Линейный Оператор(действует на множестве функций имеющих производную до n-го порядка включительно).линейное неоднородное уравнение будем записывать в виде 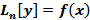, а однородное