2.(линейность) Если , и сходятся ,то сходится и равен

Дата: 2025-05-25; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

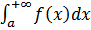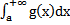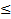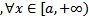3.Если и сходятся, f(x) g(x) ,то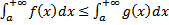

4. Если существуют 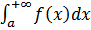и 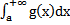, то существует.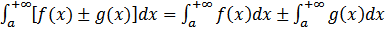

КРИТЕРИЙ КОШИ СХОДИМОСТИ ИНТЕГРАЛА.

Для сходимости интеграла 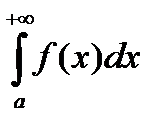необходимо и достаточно выполнения условия :

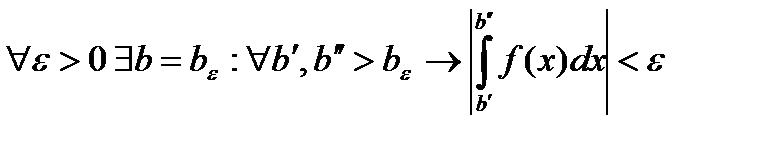
ДОК. Сходимость интеграла равносильна существованию предела 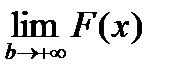, где

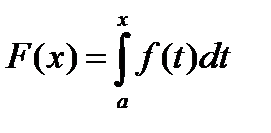- первообразная функции 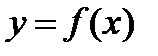на 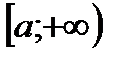. Для существования 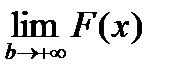необходимо и достаточно по критерию Коши для предела функции, чтобы

.

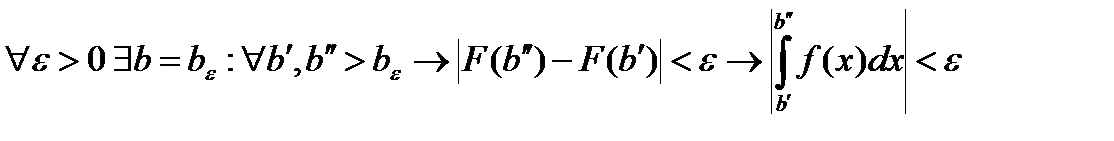Сформулируем теоремы сравнения 1 и 2 для несобственных интегралов на .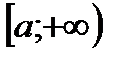

Признак сравнения по неравенству. Пусть функции f(x) и g(x) интегрируемы по любому отрезку [a,b] и при 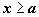удовлетворяют неравенствам 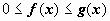. Тогда:
если сходится интеграл 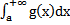, то сходится интеграл ;
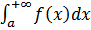если расходится интеграл 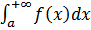, то расходится интеграл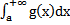

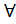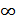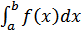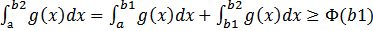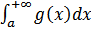Док-во:g(x)≥0, xϵ[a,+ ) Покажем, что Ф(b)= неубывает. Пусть b1<b2,Ф(b2)= Пусть сходится =>

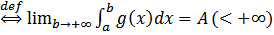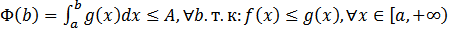
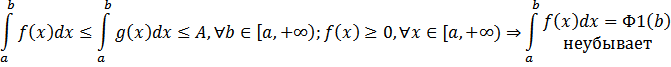
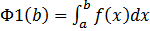неубывает и ограниченно сверху 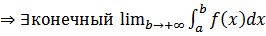.Пусть 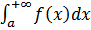расходится д.п. 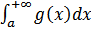сходится 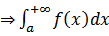сходится!!!!!!!ПРОТИВОРЕЧИЕ

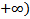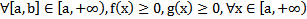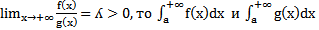(Предельный признак сравнения )Пусть f(x) и g(x) определены на [a, интегрируемы на если сходится или расходится одновременно.Док-во: 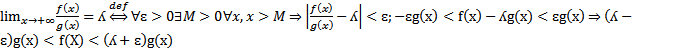выберем ɛ так ,что ʎ+ɛ>0.1) пусть 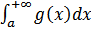сходится 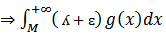сходится(свойство линейности) 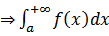сходится .

(теорема о сходимости абсолютно сходящегося интеграла) В некоторых приложениях несобственных интегралов возникает необходимость использования углубленного понятия сходимости. (Одно из таких приложений рассматривается в разделе "Интегралы, зависящие от параметра".) С этой целью рассмотрим следующие возможные случаи.

1. Пусть функция f(x) интегрируема на полубесконечном интервале [A, ∞). Если наряду с интегралом 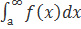сходится и интеграл 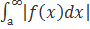, то интеграл 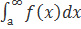называется абсолютно сходящимся. Говорят также, что функция f(x) абсолютно интегрируема на промежутке [A, ∞).

2. Если интеграл 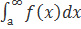сходится, тогда как интеграл 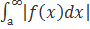расходится, то интеграл 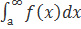называется условно сходящимся.

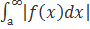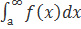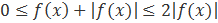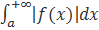Заметим, что из сходимости интеграла вытекает сходимость интеграла , тогда как обратное утверждение является несправедливым.Док-во:Предпологается что функция f(x) определена при : т.к. по условию сходится, то сходится и интеграл 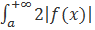следовательно, по признаку сравнения сходится интеграл 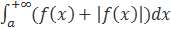НО тогда сходится интеграл 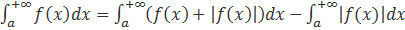ЧТД.

Определенный интеграл от неограниченной на отрезке функции не существует; функцию, заданную на неограниченном промежутке, нельзя проинтегрировать по этому промежутку. Эти ограничения оказываются неудобными при рассмотрении многих теоретических и прикладных задач. Поэтому возникает необходимость расширить понятие интеграла. Это делается с помощью дополнительного предельного перехода. Рассмотрим сначала интегралы по неограниченному промежутку.

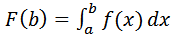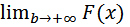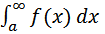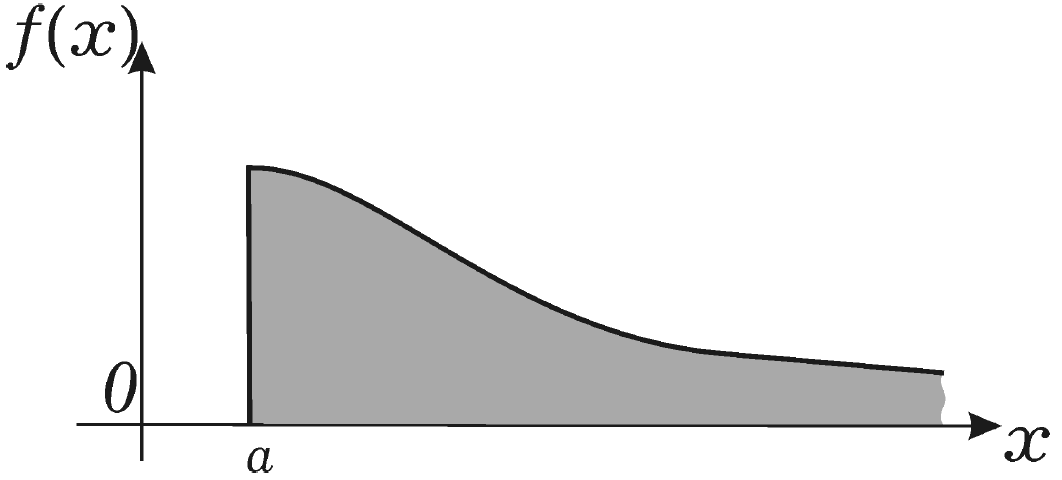
Пусть функция f(x) определена при x > a и интегрируема на любом отрезке [a, b]. Тогда на промежутке [a, +∞) определена функция Если существует (конечный) предел то этот предел называется несобственным интегралом (1-го рода) от функции f(x) по промежутку [a, +∞) и обозначается В случае существования предела последний интеграл называют сходящимся, в противном случае - расходящимся. Если f(x) > 0 и интеграл 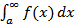сходится, то значение этого интеграла можно истолковать геометрически как площадь бесконечной криволинейной трапеции. Для функции f(x), заданной для x ≤ b и интегрируемой на любом отрезке [a, b], можно рассмотреть несобственный интеграл 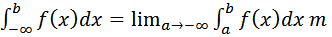Если же функция f(x) определена на всей вещественной прямой и интегрируема на любом отрезке [a, b], то, выбрав произвольно точку c на этом отрезке, можно рассмотреть несобственный интеграл 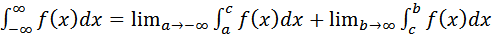Такой интеграл считается сходящимся, если существуют оба предела в правой части последнего равенства. Нетрудно проверить, что сходимость (т.е. существование) интеграла 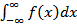и его значение не зависят от выбора точки c. Из определений несобственных интегралов следует, что для непрерывной функции f(x) в случае сходимости соответствующих интегралов справедливы следующие обобщения формулы Ньютона-Лейбница: 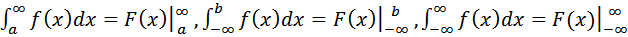где F(x) - первообразная функции f(x) на соответствующем промежутке

Вопрос 15

(Сформулировать определение несобственного интеграла 2-го рода и признаки сходимости таких интегралов)

Пусть функция f(x) определена на [a, b) и интегрируема на любом отрезке [a.n] 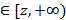, неограничена при 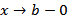.Несобственный интеграл от функции f(x) по промежутку [a,b) называется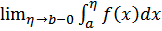

называется несобственным интегралом (2-го рода) от неограниченной функции f(x) по промежутку [a, b) и обозначается: 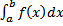(интеграл 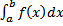называют сходящимся если предел существует и конечен, и расходящемся есть предел равен бесконечности или не существует).Если F(x) первообразная f(x) на [a,b), то 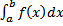= 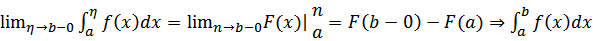сходится тогда и только тогда когда существует конечный .

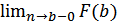- Теорема (признак сравнения):

Пусть функции f(x) и g(x) интегрируемы на отрезке [a, b] при любом b, и пусть для любого x ≥ a выполняется неравенство 0 ≤ f(x) ≤ g(x).

Тогда из сходимости интеграла 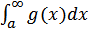следует сходимость интеграла 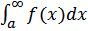, а из расходимости 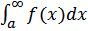, следует расходимость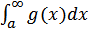

- Доказательство:

Из неравенства f(x) ≤ g(x) следует, что для любого b

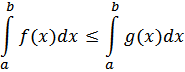
Если второй из этих интегралов сходится, то, ввиду неотрицательности g(x) для некоторой константы C при всех b a выполняется неравенство 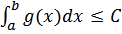. Но тогда из предыдущего неравенства для интегралов следует, что при b ≥ a: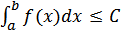

Если интеграл 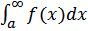расходится, а интеграл 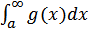сходится, то мы получаем противоречие с только что доказанным. Поэтому расходимость первого интеграла влечет

расходимость второго, Теорема доказана.

-Теорема (признак сравнения в предельной форме):

Пусть функции f(x) и g(x) положительны при x ≥ a и интегрируемы на любом отрезке [a, b]. Тогда, если существует предел

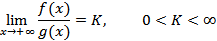
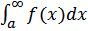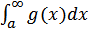то интегралы и сходятся или расходятся одновременно.

-Доказательство:

В теореме содержатся четыре утверждения. Докажем лишь одно из них: если интеграл 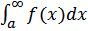сходится, то сходится и интеграл 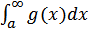. Возьмем 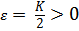. Тогда при всех x ≥ 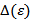выполняется неравенство

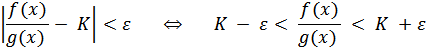
Т.к. 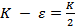, то отсюда следует, что при всех указанных x выполняется неравенство g(x) < f(x). На основании предыдущей теоремы получаем, что сходится интеграл

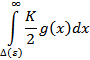
а тогда сходится и интеграл 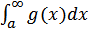. Остальные утверждения теоремы доказываются аналогично. Теорема доказана.

Замечание :

Из этой теоремы вытекает, что если f(x) и g(x) положительны (по крайней мере для достаточно больших x) и являются эквивалентными бесконечно малыми при 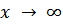, то интегралы от этих функций указанного вида сходятся или расходятся одновременно.

-Теорема (о сходимости абсолютно сходящегося интеграла):

Если интеграл 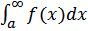сходится абсолютно, то он сходится.

-Доказательство:

Здесь, как обычно, предполагается, что функция f(x) определена при x ≥ a и интегрируема на каждом отрезке [a, b]. Напишем очевидное неравенство, верное для любого x ≥ a :

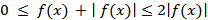
Т.к. 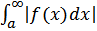по условию сходится, то сходится и интеграл 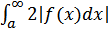. Следовательно, по признаку сравнения сходится интеграл

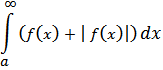
Но тогда сходится и интеграл

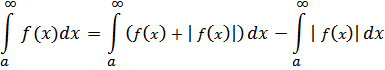
Теорема доказана.

Вопрос 16

(Фигура ограничена кривой y = f ( x ) ≥ 0, прямыми x = a , x = b и y = 0. Вывести формулу для вычисления с помощью определенного интеграла площади этой фигуры)

Рассмотрим вопрос о вычислении площади с помощью определенного интеграла. Выше было установлено, что при f(x) > 0 площадь S соответствующей криволинейной трапеции вычисляется по формуле 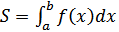Если на отрезке [a, b] функция f(x) неположительная, т.е. 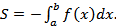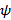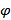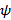f(x) ≤ 0, то, очевидно, Пользуясь этими замечаниями, нетрудно установить, что если плоская геометрическая фигура ограничена сверху и снизу соответственно графиками непрерывных функций (x) и (x), (x) > 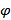(x), a ≤ x ≤ b, а с боков - отрезками прямых x = a и x = b, то площадь S этой фигуры вычисляется по формуле 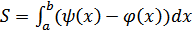Если плоская кривая задана параметрически, т.е. в виде x = 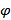( x ), y = 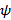( x ), 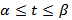причем 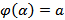, , 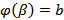a < b , 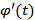> 0 на [a , b]

то эту же кривую можно задать и явным уравнением y = y ( x ), a ≤ x ≤ b

где y(x) = 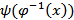; 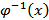− функция, обратная по отношению к 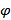(t). Все это хорошо известно из начального курса анализа.Если y(x) > 0, то площадь S соответствующей криволинейной трапеции можно вычислить следующим образом: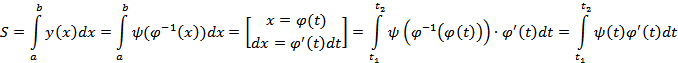

Т.о., в данном случае справедлива формулa 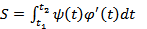Нетрудно видеть, что при 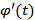< 0 эта формула справедлива лишь с точностью до знака; поэтому в общем случае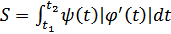

Вопрос 17

(Фигура ограничена лучами 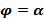, 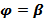и кривой 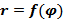. Здесь r и 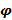– полярные координаты точки, 0 ≤ α < β ≤ 2 π . Вывести формулу для вычисления с помощью определенного интеграла площади этой фигуры)

Криволинейным сектором называется геометрическая фигура, ограниченная отрезками лучей 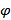= α, 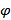= β и кривой r = r( 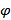), 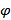∈ [α, β]