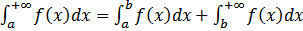Из двух написанных равенств следует утверждение теоремы. Теорема доказана.
Вопрос 1
(Сформулировать определение первообразной. Сформулировать свойства первообразной и неопределенного интеграла)
функция F ( x ) называется первообразной функции f ( x ) на интервале от (а, b ) если:
1) F ( x ) дифференцируема на (а, b ).
2) F ( x )’= f ( x ) и существует х Є(а, b ).
Теор. Пусть F 1 ( x ) и F 2 ( x )- первообразные функции f ( x ) на ( a , b ).Тогда F 1 (х)= F 2 ( x )+ C . (две первообразные одной функции отличаются на константу)
Док-во: Рассмотрим функцию Ф(х)= F 1 ( x )- F 2 ( x ) => Ф’( x )= F ’1( x )- F ’2( x )= f ( x )- f ( x )=0 для любого Х из интервала (а,в). Покажем что если Ф’( x )= C = const для любого Х из интервала (а,в). Пусть х1,х2 принадлежат интервалу (а,в), х1<х2: Тогда согласно теореме Лагранжа Ф(х2)-Ф(х1)=Ф’(₰)(х2-х1),Ф’( x )=0 для любого Х из интервала (а,в)=>Ф’(₰)=0=> Ф(х2)-Ф(х1)=0 для любого Х из интервала (а,в) ó Ф(х)=С=> F 1 (х)= F 2 ( x )+ C .Таким образом, вся совокупность первообразных функции f(x) описывается выражением F(x) + C, где F(x) — какая-либо фиксированная первообразная, а C — произвольная постоянная. Совокупность всех первообразных функции f(x) (на некотором промежутке) называется неопределенным интегралом и обозначается 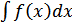
Свойства неопределенного интеграла:
1) 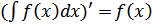 ,
, 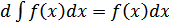 ;
;
2 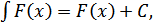 где F ( x )= df ( x )
где F ( x )= df ( x )
3) 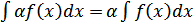 α ≠ 0;
α ≠ 0;
4) 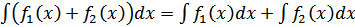
Вопрос 2
(Разложение правильной рациональной дроби на простейшие. Интегрирование простейших дробей)
1) Разложение правильной рациональной дроби на простейшие или метод неопределенных коэффициентов
B курсе высшей алгебры доказывается, что всякая правильная рациональная дробь P(x)/Q(x), знаменатель которой записывается в виде:
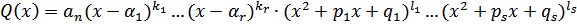
где 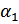 , ...,
, ..., 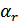 ,
, 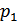 , ...,
, ..., 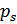 ,
, 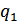 , ...,
, ..., 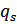 − вещественные числа; квадратные трехчлены не имеют
− вещественные числа; квадратные трехчлены не имеют
вещественных корней, и 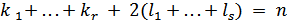 .
.
следующим образом представляется в виде суммы простейших дробей.
При этом если многочлен Q(x) не имеет вещественных корней, то в написанном разложении отсутствуют линейные множители, а если все корни этого многочлена вещественны, то отсутствуют квадратные трехчлены. Отметим еще, что разложение единственно (с точностью до порядка сомножителей).
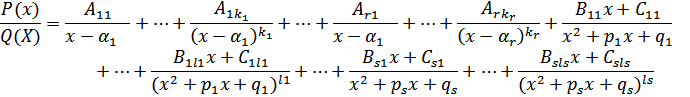
Интегрирование простейших дробей
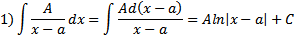
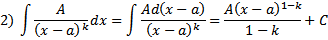
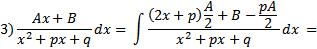
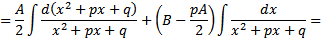
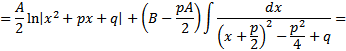
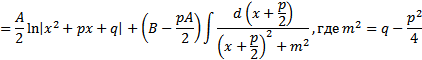
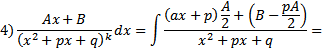
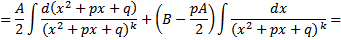
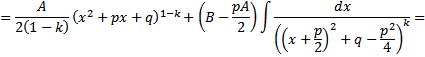
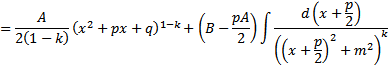
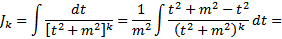
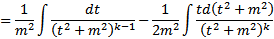
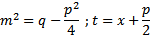
Вопрос 3
(Сформулировать свойства определенного интеграла. Доказать теорему о сохранении определенным интегралом знака подынтегральной функции)
1) 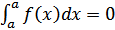 ;
;
2) 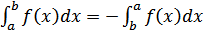 ;
;
2a) Если f ( x ) и g ( x ) интегрируемы на [a , b], то и 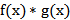 и
и 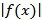 интегр. на [a , b];
интегр. на [a , b];
3) Линейность. Пусть функции f1(x) и f2(x) интегрируемы на отрезке [a, b], и пусть α1 и α2 - произвольные вещественные числа. Тогда функция α1f1(x) + α2f2(x) также интегрируема на [a, b], и
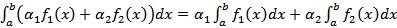
Док-во: для любого разбиения отрезка и любого выбора точек 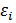 выполняется
выполняется 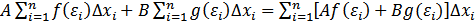 . Перейдем в этом равенстве к пределу при
. Перейдем в этом равенстве к пределу при 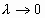 . Так как существуют пределы интегральных сумм, стоящих в левой части равенства, то существует предел линейной комбинации этих сумм, следовательно, существует предел правой интегральной суммы, откуда следует истинность и утверждения, и равенства.
. Так как существуют пределы интегральных сумм, стоящих в левой части равенства, то существует предел линейной комбинации этих сумм, следовательно, существует предел правой интегральной суммы, откуда следует истинность и утверждения, и равенства.
4) Если f ( x ) интегрируема на [a , b], то f ( x ) интегрируема на любом отрезке [α , β] 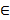 [a , b];
[a , b];
5) Аддитивность. Пусть функция f(x) интегрируема на отрезках [a, c] и [c, b]. Тогда она интегрируема и на отрезке [a, b], причем 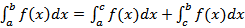 ;
;
Док-во. Если f(x) удовлетворяет условиям интегрируемости по отрезку[a,b], то она удовлетворяет условиям интегрируемости по отрезкам [a,c] и [c,b]. Будем брать такие разбиения отрезка[a,b], чтобы точка c являлась одним из узлов xi:c=xi0,. Тогда. 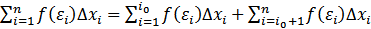 В этом равенстве первая сумма справа - интегральная сумма для
В этом равенстве первая сумма справа - интегральная сумма для 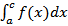 , вторая - для
, вторая - для 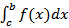 . Переходим к пределу при
. Переходим к пределу при 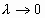 . Пределы для всех трёх сумм существуют, и
. Пределы для всех трёх сумм существуют, и 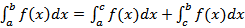 .
.
6) Пусть функции f1(x) и f2(x) интегрируемы на отрезке [a, b], и пусть в каждой точке x этого отрезка выполняется неравенство f1(x) ≤ f2(x). Тогда 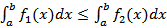 ;Док-во: Для любого разбиения отрезка и любого выбора nочек
;Док-во: Для любого разбиения отрезка и любого выбора nочек 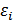 при
при 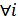 .
. 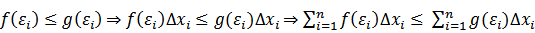 Переходя в этом неравенстве к пределу при
Переходя в этом неравенстве к пределу при 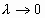 , получаем требуемое неравенство.
, получаем требуемое неравенство.
7) Теорема (об оценке)
Значение определенного интеграла заключено между произведениями наименьшего и наибольшего значений подынтегральной функции на длину интервала интегрирования, т.е. 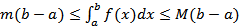
где M и m - соответственно наименьшее и наибольшее значения функции f(x) в интервале [a, b];Док-во: Докажем левое неравенство (цифрами над знаками импликации обозначены номера применяемых ранее доказанных свойств): 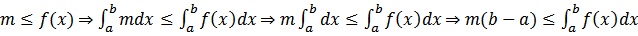 . Аналогично доказывается и правое неравенство.
. Аналогично доказывается и правое неравенство.
8)Теорема (об оценке модуля определенного интеграла)
Пусть функция f(x) интегрируема на отрезке [a, b] . Тогда функция |f(x)| также интегрируема на этом отрезке, и 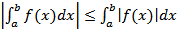 Док-во
Док-во 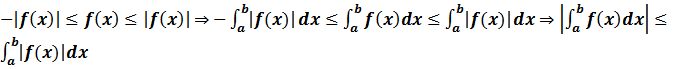 .
.
9) Терема( о среднем)
Пусть функция f(x) непрерывна на отрезке [a, b] . Тогда существует точка ξ ∈ [a, b] такая, что 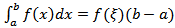 Док-во. Функция, непрерывная на отрезке, принимает на этом отрезке своё наименьшее m и наибольшее M значения. Тогда
Док-во. Функция, непрерывная на отрезке, принимает на этом отрезке своё наименьшее m и наибольшее M значения. Тогда 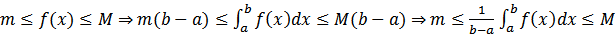 . Число
. Число 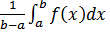 заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между m и M. Таким образом, существует точка
заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между m и M. Таким образом, существует точка 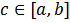 , такая что
, такая что 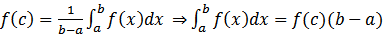 .
.
10) -Теорема (о сохранении определенным интегралом знака подынтегральной функции)
Если f ( x ) интегрируема на [a , b] и f ( x ) 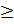 0 и
0 и 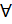 x Є[a , b], то
x Є[a , b], то 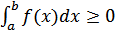
-Доказательство:
Составим сумму 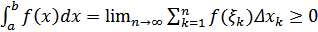 т.к. f (
т.к. f ( 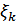 )
) 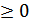 и
и 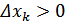
Что и требовалось доказать!
Вопрос 4
(Доказать теорему об оценке определенного интеграла)
- Теорема:
Значение определенного интеграла заключено между произведениями наименьшего и наибольшего значений подынтегральной функции на длину интервала интегрирования, т.е. 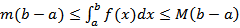 где M и m - соответственно наименьшее и наибольшее значения функции f(x) в интервале [a, b];
где M и m - соответственно наименьшее и наибольшее значения функции f(x) в интервале [a, b];
- Доказательство:
Возьмем две функции M−f(x) и m−f(x). Первая из них в интервале [a, b] неотрицательна, вторая неположительна. Значит по теореме о знаке интеграла:
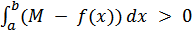 и
и 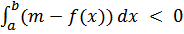
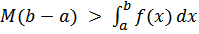 и
и 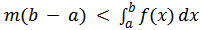
что и требовалось доказать. Из доказательства теоремы о знаке интеграла следует, что знаки неравенств могут перейти в знаки равенств только в том случае, когда функция f(x) постоянна.
Вопрос 5
(Доказать теорему об оценке модуля определенного интеграла)
Пусть функция f(x) интегрируема на отрезке [a, b]. Тогда функция |f(x)| также интегрируема на этом отрезке, и 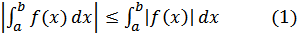
-Доказательство:
Факт интегрируемости функции |f(x)| нетрудно доказать для кусочно-непрерывной функции f(x); в общем случае принимаем это без доказательства (сама теорема принимается без доказательств). Запишем очевидное неравенство для интегральных сумм: 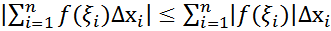 .Переходя к пределу при стремлении к нулю диаметра разбиения, получаем требуемое.
.Переходя к пределу при стремлении к нулю диаметра разбиения, получаем требуемое.
Заметим, что (1) можно обобщить и на случай a > b. В этом случае соответствующее неравенство приобретает вид: 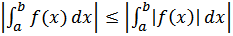
Вопрос 6
- Теорема:
Пусть функция f(x) непрерывна на отрезке [a, b]. Тогда существует точка ξ ∈ [a, b] такая, что 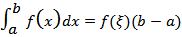 - Доказательство:
- Доказательство:
Т.к. f(x) непрерывна на [a, b], то эта функция достигает на этом отрезке своего наименьшего значения m и наибольшего значения M и принимает все значения из отрезка [m, M]. Далее, из неравенства m ≤ f(x) ≤ M получаем, что 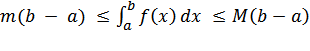 Или
Или 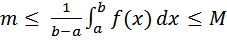 Поэтому существует число ξ ∈ [a, b] такое, что
Поэтому существует число ξ ∈ [a, b] такое, что 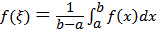 Отсюда легко следует требуемое. Теорема доказана.
Отсюда легко следует требуемое. Теорема доказана.
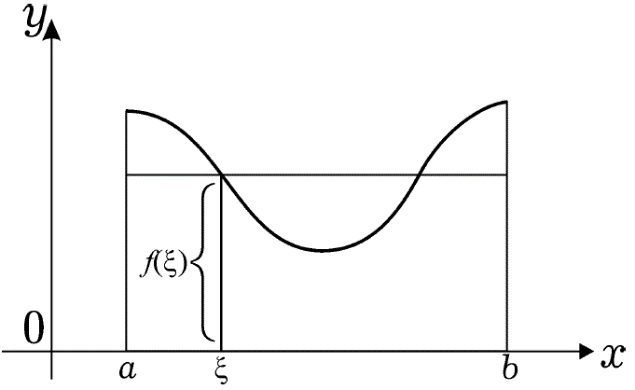
-Геометрический смысл:
доказанной теоремы заключается в том, что на отрезке [a, b] найдется точка ξ такая, что площадь соответствующей криволинейной трапеции равна площади прямоугольника с основанием (b – a) и высотой f(ξ); при этом предполагается, что f(x) неотрицательна на [a, b]
 Вопрос 7
Вопрос 7
(Доказать теорему о производной от интеграла по его верхнему пределу)
-Определение: Если функция f(x) интегрируема на отрезке [a, b], то для любого x, a ≤ x ≤ b, существует интеграл 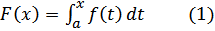
который называется интегралом с переменным верхним пределом.
-Теорема:
Пусть функция f(x) интегрируема на отрезке [a, b] и непрерывна в некоторой точке x этого отрезка. Тогда функция (1) дифференцируема в точке x, и F ’( x )= f ( x )
- Доказательство: Достаточно доказать, что
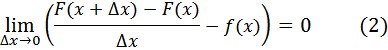
Оценим сверху модуль выражения под знаком предела в левой части этого равенства;
имеем: 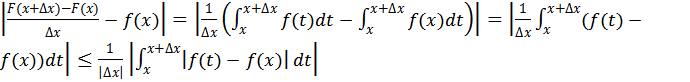 Т.к. функция f непрерывна в точке x, то для любого
Т.к. функция f непрерывна в точке x, то для любого 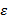 > 0 существует число
> 0 существует число 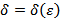 > 0 такое, что при любом t, t-x <
> 0 такое, что при любом t, t-x < 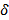 , выполняется неравенство
, выполняется неравенство 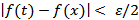 Поэтому для указанных t
Поэтому для указанных t 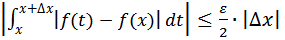 Окончательно
Окончательно 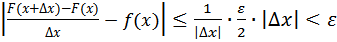
если 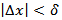 . Это означает справедливость (2). Теорема доказана.
. Это означает справедливость (2). Теорема доказана.
-Следствие: Если функция f(x) непрерывна на отрезке [a, b], то она имеет на этом
отрезке первообразную. В качестве такой первообразной можно взять, например, интеграл
с переменным верхним пределом.
Вопрос 8
(Вывести формулу Ньютона-Лейбница)
- Теорема:
Если функция f(x) непрерывна на отрезке [a, b], и 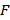 (x) - какая-либо первообразная этой функции на указанном отрезке, то
(x) - какая-либо первообразная этой функции на указанном отрезке, то 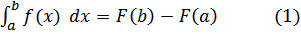
-Доказательство:
Одной из первообразных функции f(x) является 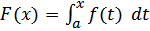
две первообразные функции f(x) различаются самое большее на константу, т.е. 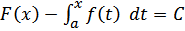 Подставляя сюда x = a , получаем, что C =
Подставляя сюда x = a , получаем, что C = 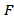 (a). Поэтому
(a). Поэтому 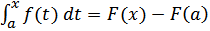 При x=b получаем требуемую формулу. Теорема доказана.
При x=b получаем требуемую формулу. Теорема доказана.
Доказанную теорему часто называют основной теоремой интегрального исчисления. Формула (1) называется формулой Ньютона-Лейбница; эту формулу часто записывают в виде 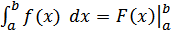 правую часть при этом называют двойной подстановкой от a до b. Заметим еще, что формула Ньютона-Лейбница справедлива и при a ≥ b.
правую часть при этом называют двойной подстановкой от a до b. Заметим еще, что формула Ньютона-Лейбница справедлива и при a ≥ b.
Вопрос 9
(Сформулировать и доказать теорему об интегрировании подстановкой для определённого интеграла)
Пусть функция f(x) непрерывна на отрезке I, а функция ϕ непрерывно дифференцируема на отрезке [α, β], причем ϕ(t) ∈ I для любого t ∈ [α, β]. Тогда, если a = ϕ(α), b = ϕ(β), то
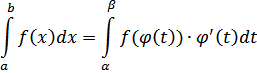
-Доказательство:
В силу сделанных предположений оба интеграла, входящие в последнее равенство, существуют. Пусть F(x) − первообразная функции f(x) на отрезке I; эта первообразная существует в силу непрерывности f(x) на I. Тогда F( 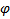 (t)) будет первообразной функции f(
(t)) будет первообразной функции f( 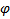 (t))
(t)) 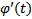 на отрезке [α, β], что проверяется непосредственно. По формуле Ньютона-Лейбница имеем
на отрезке [α, β], что проверяется непосредственно. По формуле Ньютона-Лейбница имеем 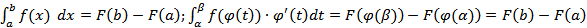
Из двух написанных равенств следует утверждение теоремы. Теорема доказана.
Вопрос 10
(Сформулировать и доказать теорему об интегрировании по частям для определенного интеграла)
Пусть функции u(x) и v(x) непрерывно дифференцируемы на отрезке [a, b]. Тогда
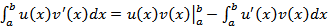 -Доказательство:
-Доказательство:
Рассмотрим функцию 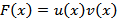 ;
; 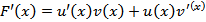 Следовательно, F(x) − первообразная для u(x)· v’(x). По формуле Ньютона-Лейбница получаем
Следовательно, F(x) − первообразная для u(x)· v’(x). По формуле Ньютона-Лейбница получаем 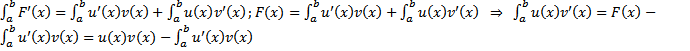
Вопрос 11
(Сформулировать свойства определенного интеграла. Интегрирование периодических функций, интегрирование четных и нечетных функций на отрезке, симметричном относительно начала координат)
-Теорема (об интеграле от периодической функции):Если периодическая с периодом T > 0 функция f(x) интегрируема на каком-либо отрезке длины T , то она интегрируема на любом отрезке, и интеграл 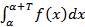 не зависит от α , f ( x + T )= f ( x ).-Доказательство:Для упрощения доказательства предположим дополнительно, что f(x) непрерывна при всех x. Напишем очевидное равенство:
не зависит от α , f ( x + T )= f ( x ).-Доказательство:Для упрощения доказательства предположим дополнительно, что f(x) непрерывна при всех x. Напишем очевидное равенство: 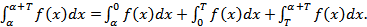 В последнем интеграле сделаем замену переменной(x=u+T,x=T => u=0;dx=du,x=a+T=>u=a):
В последнем интеграле сделаем замену переменной(x=u+T,x=T => u=0;dx=du,x=a+T=>u=a): 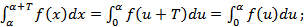 Следовательно, в равенстве:
Следовательно, в равенстве: 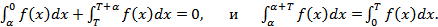 Теорема доказана.
Теорема доказана.
Пусть f(x) интегрируема на отрезке [−α; α]. Тогда 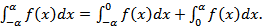 Предположив, что функция f(x) непрерывна, сделаем в первом интеграле замену x = −t; получим:
Предположив, что функция f(x) непрерывна, сделаем в первом интеграле замену x = −t; получим: 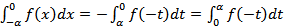 Отсюда
Отсюда 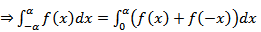 Поэтому в случае четной функции
Поэтому в случае четной функции 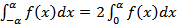 а в случае нечетной
а в случае нечетной 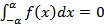
Вопрос 12, 13, 14
(Сформулировать свойства несобственного интеграла 1-го рода. Сформулировать и доказать признак сходимости по неравенству, предельный признак сравнения, признак абсолютной сходимости для несобственных интегралов 1-го рода)
Определение Предположим, что функция f(x) задана на бесконечном промежутке вида [a,+ 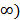 и интегрируема на любом конечном отрезке [a,b] , где
и интегрируема на любом конечном отрезке [a,b] , где 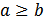 . Таким образом, можно рассмотреть функцию, зависящую от верхнего предела, как от переменной:
. Таким образом, можно рассмотреть функцию, зависящую от верхнего предела, как от переменной: 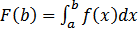
Если эта функция имеет предел при 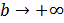 , то число
, то число 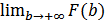 называется значением несобственного интеграла первого рода:
называется значением несобственного интеграла первого рода: 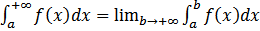 а сам определенный интеграл называется сходящимся. Если же предела не существует, то интеграл называется расходящимся и не имеет никакого числового значения.
а сам определенный интеграл называется сходящимся. Если же предела не существует, то интеграл называется расходящимся и не имеет никакого числового значения.
1.(адитивность) Если существует 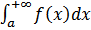 , то
, то 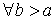 существует
существует 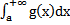 . При этом.
. При этом.